ЛР ЦОС. Лабораторные работы. Конспект лекций по курсу Цифровая обработка сигналов
 Скачать 1.16 Mb.
|
Реализовать такой фильтр можно только при условии .Из приведенного неравенства вытекает известное соотношение Котельникова, позволяющее выбрать частоту дискретизации  . (6)Если это условие не выполняется, то возникает наложение спектров. Эффект наложения спектров иллюстрируется рисунком 3.в. Из него видно, что в полосу пропускания фильтра неизбежно попадает спектральная составляющая, которой нет в спектре исходного аналогового сигнала. Это вызывает искажение восстановленного сигнала. 3. Дискретизация апериодических аналоговых сигналов Известно, что спектр  апериодического аналогового сигнала x(t) определяется с использованием прямого преобразования Фурье (7)Для определения дискретного сигнала сначала преобразуем соотношение (3)  Воспользовавшись прямым преобразованием Фурье, найдем спектр дискретного сигнала 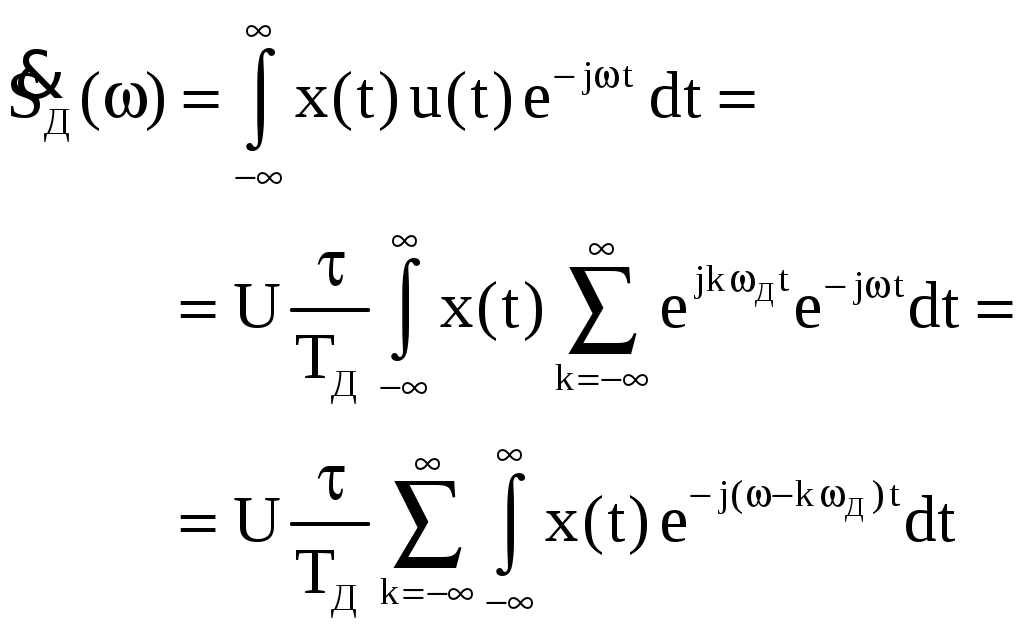 Сравнивая последнее соотношение с (6), выразим спектр дискретного сигнала через спектр аналогового сигнала  (8)Таким образом, спектр дискретного сигнала с точностью до постоянного сомножителя Uτ / TД равен сумме спектров аналогового сигнала, сдвинутых вдоль оси частот на kωД. На рисунке 4 показаны спектры апериодического аналогового сигнала до и после дискретизации как в области положительных, так и в области отрицательных частот. Их отличие от линейчатых спектров периодического аналогового сигнала состоит в том, что спектральная плотность апериодического сигнала представляет собой непрерывную функцию частоты. 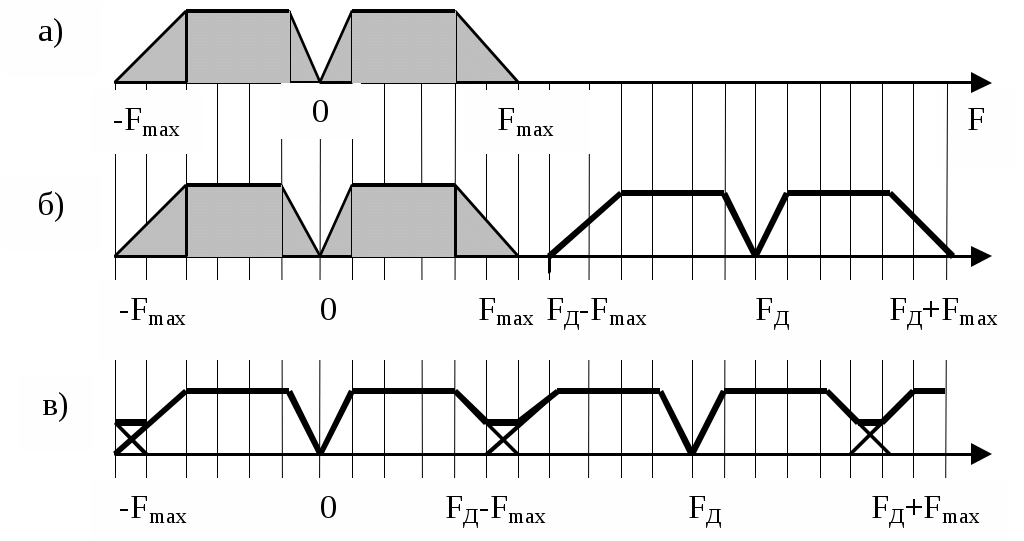 Рисунок 4 – Спектры апериодического аналогового сигнала до дискретизации (а), после дискретизации при отсутствии (б) и при наличии (в) наложения спектров Как видно из рисунка при FД < 2Fmax имеет место эффект наложения сгустков спектра дискретного сигнала. В случае, когда нельзя по каким - либо причинам увеличить частоту дискретизации сигнала с ограниченным спектром, или аналоговый сигнал имеет неограниченный спектр, для уменьшения ошибки наложения спектров требуется предварительное ограничение спектра аналогового сигнала. Из рисунка 5 видно, что при этом ошибка наложения уменьшается. 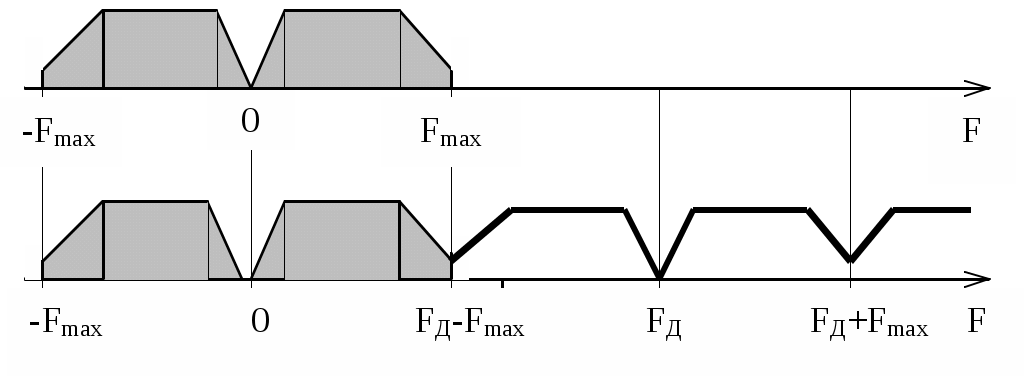 Рисунок 5 – Уменьшение ошибки наложения за счет ограничения спектра аналогового сигнала 4. Дискретизация узкополосных модулированных сигналов Особый интерес представляет случай дискретизации модулированных сигналов, когда результатом цифровой обработки должно быть выделение модулирующей функции. Покажем, что при этом частота дискретизации может быть выбрана ниже частоты несущей. На рисунке 6 показан спектр аналогового синусоидального сигнала с частотой f0 > FД до (а) и после (б) дискретизации. Спектр дискретного сигнала получен в соответствии с соотношением (4). 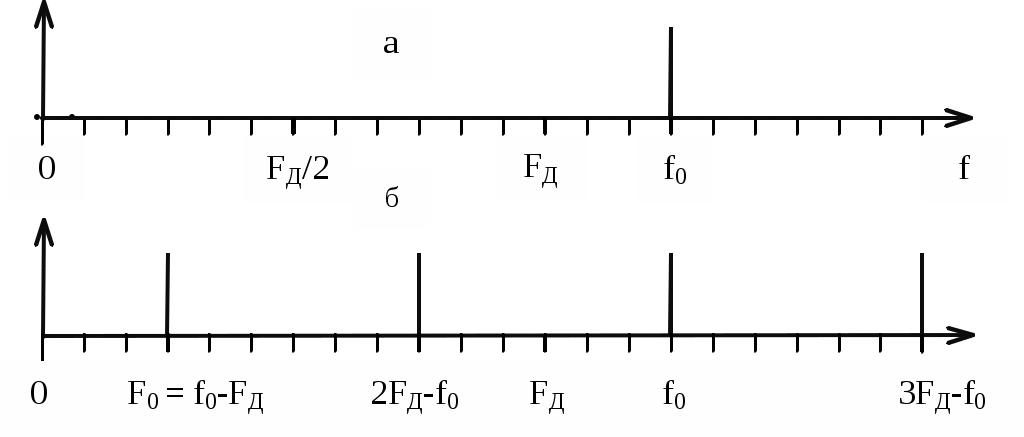 Рисунок 6 – Спектр дискретной синусоиды до (а) и после (б) дискретизации. Частота синусоиды выше частоты дискретизации Как и в случае, представленном на рис.2 при F < FД / 2, спектр дискретного сигнала представляет собой периодическую функцию частоты. Вблизи частот kFД имеются спектральные составляющие, отстоящие на величину F0. Важно отметить, что в интервале частот  - интервале Котельникова - появляется составляющая спектра с частотой F0=f0-FД.На рисунке 7 показаны временные диаграммы синусоидального сигнала x(t) до (пунктир) и после дискретизации xд(t) при дискретизации с частотой, которая меньше частоты сигнала. Из рисунка видно, что частота дискретного синусоидального сигнала существенно меньше частоты сигнала на входе дискретизатора. Она равна частоте спектральной составляющей спектра дискретного сигнала, которая попадает в интервал Котельникова. 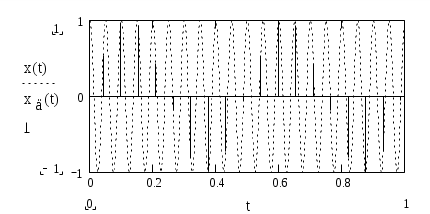 Рисунок 7 – Синусоидальное колебание на входе и выходе дискретизатора при дискретизации с частотой, меньшей частоты входного сигнала На рисунке 8 изображен спектр модулированного колебания до и после дискретизации. Из него видно, что в интервале Котельникова существует спектр, который по форме не отличается от спектра исходного аналогового сигнала, следовательно, закон модуляции сигнала после дискретизации остался неизменным, изменилась только частота несущей (F0 вместо f0), частота дискретизации должна удовлетворять условию  . (9) Последнее условие является необходимым, но недостаточным для обоснованного выбора частоты дискретизации. 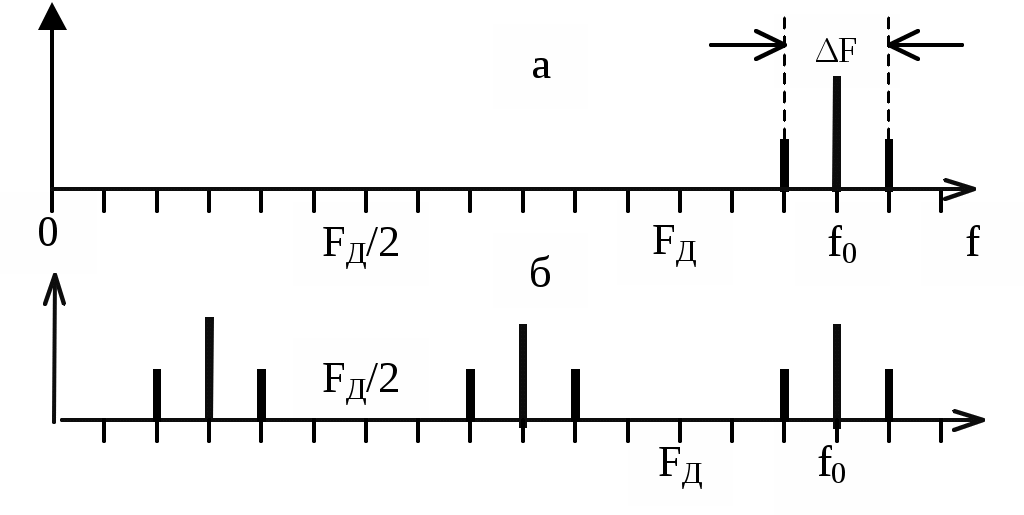 Рисунок 8 – Спектр модулированного сигнала до (а) и после (б) дискретизации При обработке сигналов в реальном масштабе времени стремятся выбрать минимально возможное значение частоты дискретизации для того, чтобы увеличить время обработки, которое не должно превышать период дискретизации. На рисунке 9 показан случай, когда 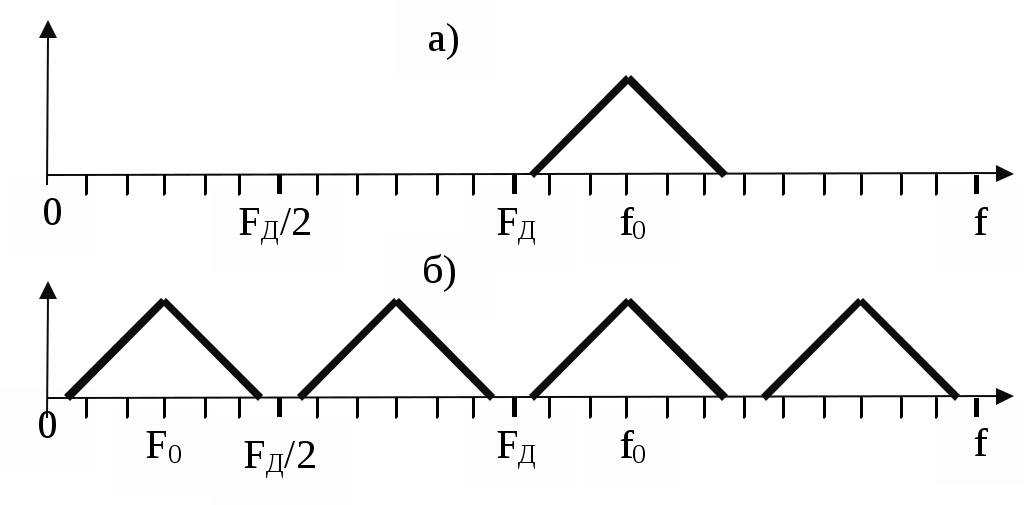 и сгустки спектра равномерно расположены вдоль оси частот. При этом частота несущей, приведенная в интервал Котельникова, равна  . Для того чтобы получить такое значение приведенной частоты несущей дискретного сигнала, частота несущей аналогового сигнала  должна отличаться от частоты дискретизации или ее гармоники на частоту  .  Рисунок 9 – Спектр сигнала до и после дискретизации при F0 = FД / 4 Спектральные диаграммы, приведенные на рисунках 10 и 11, показывают, что если это условие не выполняется, то сгустки спектра распределяются по оси частот неравномерно, в результате чего возникает наложение спектров, приводящее к искажению сигнала. Таким образом, второе условие выбора частоты дискретизации выражается следующим соотношением 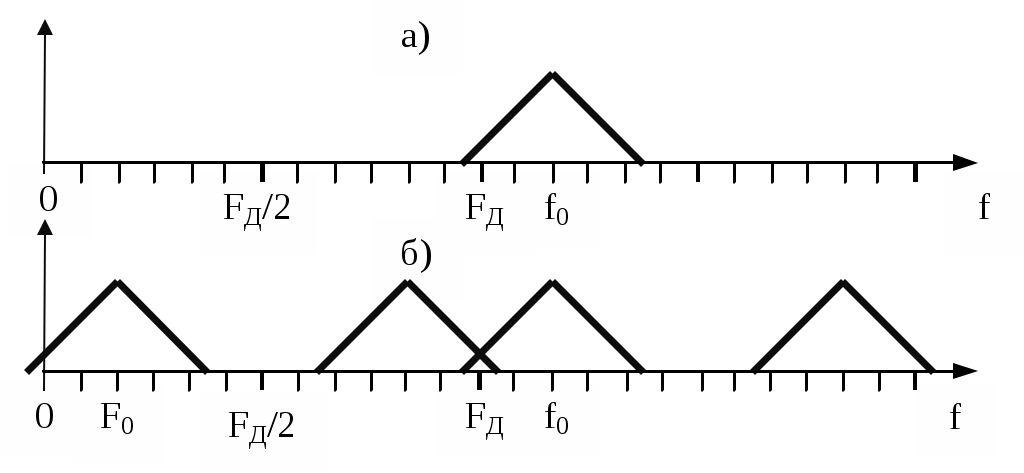 , где  (10) Рисунок 10 – Спектр сигнала до и после дискретизации при F0 < FД /4 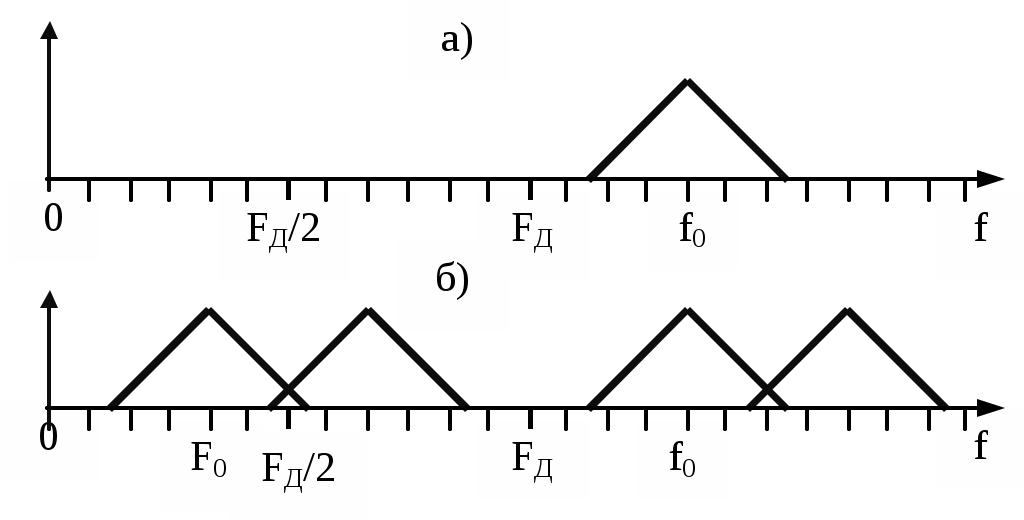 Рисунок 11 – Спектр сигнала до и после дискретизации при F0 > FД/4 В ряде случаев только часть спектра колебания, действующего на входе дискретизатора, принадлежит полезному сигналу. Например, это имеет место при использовании одного аналогового фильтра для нескольких сигналов с разной шириной спектра и последующего применения разных цифровых фильтров для выделения каждого сигнала. Этот случай показан на рисунке 12. 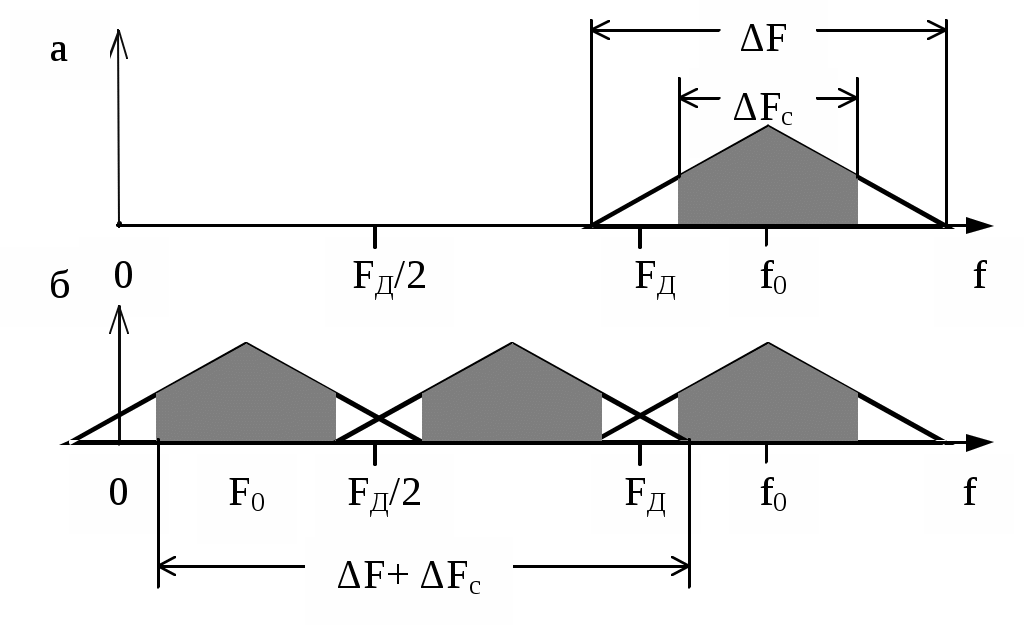 Рисунок 12 – Спектры сигнала до и после дискретизации при FД = ΔF+ ΔFc Из рисунка видно, что в данном случае можно разрешить наложение сгустков спектра там, где отсутствует спектр полезного сигнала, учитывая последующую селекцию сигнала цифровым фильтром. При этом вместо условия FД > 2 ΔF достаточно выполнить условие FД > ΔF + ΔFс (11) Приложение Б к лабораторной работе №1 Программа моделирования процесса дискретизации аналоговой синусоиды и её восстановления из дискретной 1 // Программа "Diskret1.sce" Моделирование процесса 2 // дискретизации аналоговой синусоиды и её восстановления 3 // из дискретной 4 // 5 // Ввод исходных данных для моделирования 6 // 7 X=1; // Амплитуда синусоидального колебания 8 is=512; // Количество расчетных точек в периоде синусоиды 9 delta_t=1/512 // Временной интервал между двумя соседними 10 // расчетными точками 11 id=64; // Количество расчетных точек в периоде дискретизации 12 N=2^13; // Количество расчетных точек 13 imax=1000; // Количество расчетных точек, используемых при 14 // построении временных диаграмм 15 // 16 // Расчет частоты синусоиды и частоты дискретизации 17 F=1/(delta_t*is); // Частота синусоидального колебания 18 Td=delta_t*id; // Период дискретизации 19 Fd=1/Td; // Частота дискретизации 20 // Начальная установка (обнуление массивов) 21 x=zeros(1:N); 22 u=zeros(1:N); 23 xd=zeros(1:N); 24 sv=zeros(1:N); 25 xv=zeros(1:N); 26 for i=1:N 27 //Формирование аналоговой синусоиды 28 x(i)=X*sin(2*%pi*i/is); 29 //Формирование последовательности единичных отсчетов 30 if (i/id)-floor(i/id)==0 then 31 u(i)=1; 32 else u(i)=0; 33 end 34 // Дискретизация аналоговой синусоиды 35 xd(i)=x(i)*u(i); 36 end; 37 // Определение спектра аналоговой синусоиды 38 s=fft(x); 39 // Определение спектра дискретной синусоиды 40 sd=fft(xd); 41 // Восстановление аналоговой синусоиды из дискретной 42 k1=floor(0.5*N/id); 43 for k=1:N 44 if k 45 sv(k)=sd(k); 46 else 47 sv(k)=0; 48 end 49 end 50 xv=ifft(sv); 51 // Формирование временных и спектральных диаграмм 52 x0=zeros(1:imax); 53 u0=zeros(1:imax); 54 xd0=zeros(1:imax); 55 xv0=zeros(1:imax); 56 for i0=1:imax 57 x0(i0)=x(i0); 58 u0(i0)=u(i0); 59 xd0(i0)=xd(i0); 60 xv0(i0)=xv(i0); 61 end 62 kmax=5*k1; 63 k=1:kmax; 64 f=zeros(1:kmax); 65 s0=zeros(1:kmax); 66 sv0=zeros(1:kmax); 67 sd0=zeros(1:kmax); 68 f=k/(delta_t*N); 69 for k=1:kmax 70 s0(k)=s(k)*2/N; 71 sd0(k)=sd(k)*2/N; 72 end 73 xbasc(); 74 subplot(3,2,1); 75 i0=[1:imax]; 76 t=delta_t*i0; 77 plot2d(t,x0,style=[color("blue")]) 78 xtitle('Аналоговое синусоидальное колебание') 79 xgrid 80 subplot(3,2,2) 81 plot2d3(f,abs(s0),style=[color("blue")]) 82 xgrid 83 xtitle('Спектр аналоговой синусоиды') 84 subplot(3,2,3) 85 plot2d3(t,u0) 86 xtitle('Последовательность единичных отсчетов') 87 subplot(3,2,4) 88 plot2d3(t,xd0) 89 xgrid 90 xtitle('Дискретная синусоида') 91 subplot(3,2,5) 92 plot2d(f,abs(sd0),style=[color("red")]) 93 xgrid 94 xtitle('Спектр дискретной синусоиды') 95 subplot(3,2,6) 96 plot2d(t,xv0,style=[color("red")]) 97 xgrid 98xtitle('Восстановленная аналоговая синусоида') Приложение В к лабораторной работе №1 Программа моделирования процесса дискретизации случайной последовательности прямоугольных импульсов и восстановления аналогового сигнала из дискретного 1 // Программа “Diskret2.sce” Моделирование процесса 2 // дискретизации случайной последовательности прямоугольных 3 // импульсов и восстановления аналогового сигнала из дискретного 4 // 5 // Ввод исходных данных для моделирования 6 // 7 is=512; // Количество расчетных точек в элементарной посылке 8 Xmax=0.5; 9 Xmin=-0.5; 10 delta_t=1/512; 11 id=64;//Количество расчетных точек в интервале дискретизации 12 N=8192*4; 13 imax=1000; // Количество расчетных точек, используемых при 14 // построении временных диаграмм 15 // 16 // Расчет частоты дискретизации 17 Td=delta_t*id;//Интервал дискретизации 18 Fd=1/Td; //Частота дискретизации 19 // 20 //Начальная установка (обнуление массивов) 21 I=zeros(1:N); 22 x=zeros(1:N); 23 u=zeros(1:N); 24 xd=zeros(1:N); 25 x0=zeros(1:1); 26 x0=Xmax; 27 //Формирование аналогового сигнала в виде случайной 28 //последовательности элементарных посылок 29 for i=1:N 30 if (i/is)-floor(i/is)==0 then 31 I(i)=1; 32 else I(i)=0; 33 end 34 if (I(i)==1)&(rand(1)<0.5) 35 x0=Xmin; 36 elseif (I(i)==1)&(rand(1) >=0.5) 37 x0=Xmax; 38 end 39 x(i)=x0; 40 end 41 //Формирование последовательности единичных осчетов 42 for i=1:N 43 if (i/id)-floor(i/id)==0 then 44 u(i)=1; 45 else u(i)=0; 46 end 47 end 48 // Дискретизация аналогового сигнала 49 for i=1:N 50 xd(i)=x(i)*u(i); 51 end 52 // Определение спектра аналогового сигнала 53 s=fft(x); 54 // Определение спектра дискретного сигнала 55 sd=fft(xd); 56 // Восстановление аналогового сигнала из дискретного 57 k1=floor(0.5*N/id); 58 sv=zeros(1:N); 59 for k=1:N 60 if k 61 sv(k)=sd(k); 62 else 63 sv(k)=0; 64 end 65 end 66 xv=zeros(1:N); 67 xv=ifft(sv); 68 // Формирование временных и спектральных диаграмм 69 i0=[1:imax]; 70 x0=zeros(1:imax); 71 u0=zeros(1:imax); 72 xd0=zeros(1:imax); 73 xv0=zeros(1:imax); 74 for i0=1:imax 75 x0(i0)=x(i0); u0(i0)=u(i0); 77 xd0(i0)=xd(i0); 78 xv0(i0)=xv(i0); 79 end 80 kmax=5*k1; 81 k=1:kmax; 82 f=zeros(1:kmax); 83 s0=zeros(1:kmax); 84 sv0=zeros(1:kmax); 85 sd0=zeros(1:kmax); 86 f=k/(delta_t*N); 87 for k=1:kmax 88 s0(k)=s(k)*2/N; 89 sd0(k)=sd(k)*2/N; 90 end 91 xbasc(); 92 subplot(3,2,1); 93 i0=[1:imax]; 94 t=delta_t*i0; 95 plot2d(t,x0,style=[color("blue")]) 96 xtitle('Аналоговый сигнал на входе дискретизатора') 97 xgrid 98 subplot(3,2,2) 99 plot2d3(f,abs(s0),style=[color("blue")]) 100 xgrid 101 xtitle('Спектр аналогового сигнала') 102 subplot(3,2,3) 103 plot2d3(t,u0) 104 xtitle('Последовательность единичных отсчетов') 105 subplot(3,2,4) 106 plot2d3(t,xd0) 107 xgrid 108 xtitle('Дискретный сигнал') 109 subplot(3,2,5) 110 plot2d(f,abs(sd0),style=[color("red")]) 111 xgrid 112 xtitle('Спектр дискретного сигнала') 113 subplot(3,2,6) 114 plot2d(t,xv0,style=[color("red")]) 115 xgrid 116 xtitle('Восстановленный аналоговый сигнал') Приложение Г к лабораторной работе №1 Программа моделирования процесса дискретизации модулированного сигнала и восстановления аналогового сигнала из дискретного 1 // Программа “Diskret3.sce». Моделирование процесса 2 // дискретизации модулированного сигнала и восстановления 3 // аналогового сигнала из дискретного 4 // Ввод исходных данных для моделирования 5 is=512; // Количество расчетных точек в элементарной посылке 6 // сигнала 7Xmin=-0.5; // Минимальный уровень модулирующего сигнала 8 Xmax=0.5; // Максимальный уровень модулирующего сигнала 9 delta_t=1/512; // Временной интервал между соседними 10 // расчетными точками 11 is0=51; // Количество отсчетов в периоде несущей 12 id=64; // Количество расчетных точек в интервале дискретизации 13 N=2^13;// Общее количество расчетных точек 14 imax=5000; // Количество расчетных точек, используемых при 15 // построении временных диаграмм 16 // Расчет частоты дискретизации 17 Td=delta_t*id; // Интервал дискретизации 18 Fd=1/Td; // Частота дискретизации 19 // 20 // Начальная установка (обнуление массивов) 21 I=zeros(1:N); 22 xs=zeros(1:N); 23 u=zeros(1:N); 24 xd=zeros(1:N); 25 x0=zeros(1:1); 26 x0=Xmax; 27 for i=1:N 28 // Формирование аналогового сигнала в виде периодической 29 // последовательности элементарных посылок 30 if (i/is)-floor(i/is)==0 then 31 I(i)=1; 32 else I(i)=0; 33 end 34 if (I(i)==1)&(x0==Xmax) 35 x0=Xmin; 36 elseif (I(i)==1)&(x0==Xmin) 37 x0=Xmax; 38 end 39 x(i)=x0; 40 // Формирование модулированного сигнала 41 xs(i)=x(i)*sin(2*%pi*i/is0); 42 end 43 // Формирование последовательности единичных осчетов 44 for i=1:N 45 if (i/id)-floor(i/id)==0 then 46 u(i)=1; 47 else u(i)=0; 48 end 49 end 50 // Дискретизация аналогового сигнала 51 for i=1:N 52 xd(i)=xs(i)*u(i); 53 end 54 // Определение спектра аналогового сигнала 55 s=fft(xs); 56 // Определение спектра дискретного сигнала 57 sd=fft(xd); 58 // Восстановление аналогового сигнала из дискретного 59 k1=floor(0.5*N/id); 60 sv=zeros(1:N); 61 for k=1:N 62 if k 63 sv(k)=sd(k); 64 else 65 sv(k)=0; 66 end 67 end 68 xv=zeros(1:N); 69 xv=ifft(sv); 70 // Формирование временных и спектральных диаграмм 71 i0=[1:imax]; 72 xs0=zeros(1:imax); 73 u0=zeros(1:imax); 74 xd0=zeros(1:imax); 75 xv0=zeros(1:imax); 76 for i0=1:imax 77 xs0(i0)=xs(i0); 78 u0(i0)=u(i0); 79 xd0(i0)=xd(i0); 80 xv0(i0)=xv(i0); 81 end 82 kmax=5*k1; 83 k=1:kmax; 84 f=zeros(1:kmax); 85 s0=zeros(1:kmax); 86 sv0=zeros(1:kmax); 87 sd0=zeros(1:kmax); 88 f=k/(delta_t*N); 89 for k=1:kmax 90 s0(k)=s(k)*2/N; 91 sd0(k)=sd(k)*2/N; 92 end 93 xbasc(); 94 subplot(3,2,1); 95 i0=[1:imax]; 96 t=delta_t*i0; 97 plot2d(t,xs0,style=[color("blue")]) 98 xtitle('Аналоговый сигнал на входе дискретизатора') 99 xgrid 100 subplot(3,2,2) 101 plot2d3(f,abs(s0),style=[color("blue")]) 102 xgrid 103 xtitle('Спектр аналогового сигнала') 104 subplot(3,2,3) 105 plot2d3(t,u0) 106 xtitle('Последовательность единичных отсчетов') 107 subplot(3,2,4) 108 plot2d3(t,xd0) 109 xgrid 110 xtitle('Дискретный сигнал') 111 subplot(3,2,5) 112 plot2d(f,abs(sd0),style=[color("red")]) 113 xgrid 114 xtitle('Спектр дискретного сигнала') 115 subplot(3,2,6) 116 plot2d(t,xv0,style=[color("red")]) 117 xgrid 118 xtitle('Восстановленный аналоговый сигнал') Федеральное агентство связи Государственное образовательное учреждение высшего профессионального образования «Поволжский государственный университет телекоммуникаций и информатики» Кафедра радиосвязи, радиовещания и телевидения «УТВЕРЖДАЮ» Заведующий кафедрой РРТ д.т.н., профессор _________________Елисеев С.Н. «______»__________________2012г. МЕТОДИЧЕСКАЯ РАЗРАБОТКА для проведения лабораторной работы №2 ИССЛЕДОВАНИЕ ЦИФРОВОГО РЕЗОНАТОРА ПО УЧЕБНОЙ ДИСЦИПЛИНЕ «ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ» Для направления подготовки 210700 «Инфокоммуникационные технологии и системы связи» Профиль подготовки: «Сети связи и системы коммутации» Обсуждено на заседании кафедры «_____»________________2012г. Протокол №_______ 1.Цель работы Исследование влияния коэффициентов системной функции цифрового резонатора на его АЧХ, ФЧХ и импульсную характеристику, исследование селективных свойств резонатора, исследование устойчивости цифрового резонатора. 2. Литература 1.Приложение А к лабораторной работе №2 2.Конспект лекций по курсу «Цифровая обработка сигналов» 3. В.Г.Иванова, А.И.Тяжев. Цифровая обработка сигналов и сигнальные процессоры, Самара, 2008г. 3. Подготовка к лабораторной работе Изучите указанную в разделе 2 литературу и ответьте на контрольные вопросы. 4. Контрольные вопросы 1.Начертите схему цифрового резонатора, запишите разностное уравнение, описывающее резонатор, получите выражение системной функции резонатора. 2.Запишите выражение для системной функции цифрового резонатора и, используя его, получите АЧХ при А1=0. Постройте график АЧХ. 3.Запишите выражение для системной функции цифрового резонатора и, используя его, получите ФЧХ при А1=0. Постройте график ФЧХ. 4.Как влияют коэффициенты системной функции цифрового резонатора А1 и А2 на резонансную частоту, полосу пропускания и резонансный коэффициент передачи? 5.Дайте определение импульсной характеристике цифрового фильтра. Какова импульсная характеристика цифрового резонатора, как влияют на нее коэффициенты системной функции А1 и А2? 6.На общем входе трех цифровых резонаторов, отличающихся друг от друга только резонансными частотами, действует последовательность единичных отсчетов с частотой следования FД / 18. Начертите временные диаграммы сигналов на выходах резонаторов в установившемся режиме, если их резонансные частоты равны FД / 18, FД / 9, FД / 6. 7. Каким требованиям должны удовлетворять коэффициенты системной функции для того, чтобы резонатор работал устойчиво? 5. Содержание работы 1.Исследуйте влияние коэффициентов системной функции А1 и А2 на АЧХ, ФЧХ и импульсную характеристику цифрового резонатора. Первый эксперимент нужно выполнить при постоянном коэффициенте А2 и трех значениях А1 (таблица1), а второй – при постоянном А1 и трех значениях А2 (таблица 2). 2. На общий вход трех цифровых резонаторов, отличающихся друг от друга только резонансными частотами F01, F02, F03, подайте периодическую последовательность единичных отсчетов с частотой, равной минимальной резонансной частоте, и пронаблюдайте выходные сигналы резонаторов. Исследуйте влияние коэффициента системной функции А2 на выходные сигналы резонаторов. Исходные данные для выполнения эксперимента приведены в таблице 3. Таблица 1. Исходные данные для выполнения п.1 задания (эксперимент №1)
Таблица 2. Исходные данные для выполнения п.1 задания (эксперимент №2)
Таблица 3. Исходные данные для выполнения п.2 задания
3. Выполните моделирование цифрового резонатора при действии на его входе сигнала xc и помехи xp,   ,  Резонансная частота резонатора равна частоте сигнала. Результатом моделирования должны быть временные диаграммы сигнала на входе резонатора, суммы сигнала и помехи на входе резонатора, выходного сигнала резонатора. Данные для моделирования приведены в таблице 4. Исследуйте влияние коэффициента системной функции А2 на выходной сигнал резонатора. Исследуйте влияние на выходной сигнал резонатора неточности настройки резонатора на частоту входного сигнала. 4.Повторите эксперимент п.3 с новым значением коэффициента А2=1.1, не удовлетворяющим условию устойчивости. Таблица 4. исходные данные для выполнения п.3 и п.4 задания
6. Содержание отчета Отчет должен содержать: 1.Графики АЧХ, ФЧХ и импульсной характеристики цифрового резонатора и выводы о влиянии коэффициентов А1 и А2 на резонансную частоту, резонансный коэффициент передачи, полосу пропусканию и форму АЧХ ,ФЧХ и импульсной характеристики. 2.Временные диаграммы выходных сигналов цифровых резонаторов при действии на их входах последовательности единичных отсчетов (п.2 задания) и выводы о влиянии коэффициента системной функции А2 на эти сигналы. 3. Временные диаграммы сигнала и помехи на входе цифрового резонатора и временная диаграмма сигнала на его выходе. Вывод о влиянии коэффициентов системной функции на выходной сигнал резонатора. 4. Вывод о влиянии коэффициентов системной функции на устойчивость резонатора. 7. Методические указания по выполнению работы Лабораторная работа выполняется в программной среде SCILAB. Откройте программу Scilab 5.3.3. Появится Командное окно. Окно содержит меню, панель инструментов и рабочую область. Признаком того, что система готова к выполнению команды, является наличие знака приглашения (горизонтальной стрелки), после которого расположен мигающий курсор. Щелчком левой кнопки мыши откройте редактор (Инструменты – Текстовый редактор SciNotes). Появится окно для редактирования. Из редактора откройте файл Rezonator1. Появится текст программы. Программа Rezonator1 (Приложение Б к лабораторной работе №2) предназначена для исследования влияния коэффициентов системной функции цифрового резонатора на его АЧХ, ФЧХ и импульсную характеристику. В строках 4-6 осуществляется ввод исходных данных для выполнения эксперимента, затем рассчитываются нормированное значение резонансной частоты fo0, масштабный коэффициент М и количество расчетных точек N АЧХ и ФЧХ в пределах интервала Котельникова. В цикле по порядковому номеру расчетной точки m определяются системная функция H(m), АЧХ K(m) и ФЧХ phi(m) (строки 18-25). Для определения импульсной характеристики сначала формируется испытательный сигнал x в виде единичного отсчета, который подается на вход резонатора (строки 29-36). Затем этот сигнал пропускается через резонатор (строки 38-47). Выходной сигнал резонатора y представляет собой импульсную характеристику. Последующая часть программы организует выдачу графиков АЧХ, ФЧХ и импульсной характеристики. Для выполнения п.1 задания введите значение коэффициента А2 и первое значение коэффициента А1 из таблицы 1. Для наблюдения импульсной характеристики введите максимальный номер отсчета этой характеристики nmax . Первоначально значение nmax можно выбрать в пределах 100..1000, а затем скорректировать так, чтобы удобно было наблюдать импульсную характеристику. Запустите программу (Execute – Load into Scilab). Появится окно Scilab Graphic, примерный вид которого приведен на рисунке 1. На рисунке приведены две АЧХ: при масштабном коэффициенте М=1 и при рассчитанном значении M, позволяющим наблюдать АЧХ в относительном масштабе с максимальным коэффициентом передачи, равным единице. Обратите внимание на то, что при А1=0 нормированная резонансная частота равна 0.25, и на симметрию АЧХ. Поочередно введите два других значения коэффициента А1. Запишите в отчет вывод о влиянии коэффициента А1 на АЧХ, ФЧХ и импульсную характеристику. Для исследования влияния коэффициента А2 на АЧХ, ФЧХ и импульсную характеристику воспользуйтесь данными таблицы 2. Запишите в отчет вывод о влиянии коэффициента А2 на эти характеристики. 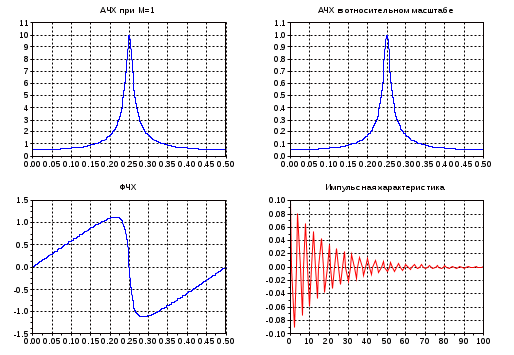 Рисунок 1 – АЧХ, ФЧХ и импульсная характеристика Для выполнения п.2 задания воспользуйтесь программой Rezonator2 и данными таблицы 3. Эта программа отличается от предыдущей тем, что в ней вместо одного моделируется три резонатора, на входах которых действует периодическая последовательность единичных отсчетов. Обратите внимание на то, что частота следования единичных отсчетов равна резонансной частоте первого резонатора, а резонансные частоты двух других резонаторов кратны резонансной частоте первого. Кроме данных таблицы 3 введите в программу максимальный номер отсчета сигнала на входах и выходах резонаторов nmax. Первоначально введите nmax в пределах 500..1000 и пронаблюдайте установившийся режим работы резонаторов. Результатом выполнения программы будут графики, вид которых показан на рисунке 2. Чтобы лучше рассмотреть форму сигналов на выходах резонаторов, уменьшите nmax. В отчете укажите, в чем сходство и в чем отличие выходных сигналов цифровых резонаторов. 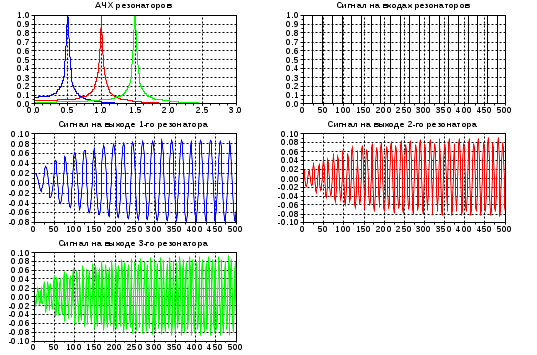 Рисунок 2- АЧХ, входной сигнал и выходные сигналы трех резонаторов Повторите эксперимент при А2=0.90. Запишите в отчет вывод о влиянии коэффициента A2 на длительность переходного процесса и постоянство амплитуды выходного сигнала в установившемся режиме. Для выполнения п.3 задания откройте программу Rezonator3 (Приложение Г к лабораторной работе №2). Программа позволяет выполнить расчет АЧХ резонатора, сформировать синусоидальный сигнал xc и две синусоидальные помехи xp на входе резонатора и определить сигнал y на его выходе. Введите исходные данные их таблицы 4. Максимальный номер отсчета входного сигнала примите равным nmax=1000. Введите значение резонансной частоты резонатора f0=fc. Запустите программу и пронаблюдайте временные диаграммы сигналов на входе и выходе резонатора, подобные тем, что приведены на рисунке 3. 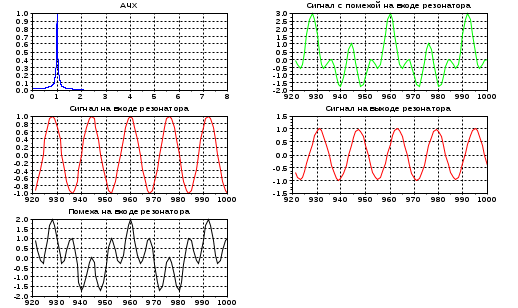 Рисунок 3 – Временные диаграммы сигналов на входе и выходе резонатора Сопоставьте временную диаграмму выходного сигнала резонатора с временной диаграммой входного сигнала, искаженного помехой и с временной диаграммой входного сигнала без помех. Результат этого сопоставления запишите в отчет. Введите новое значение коэффициента системной функции A2=0.9 и повторите эксперимент. Запишите в отчет вывод о влиянии коэффициента А2 на выходной сигнал резонатора. Установите табличное значение коэффициента А2. Не изменяя частоты сигнала, увеличьте резонансную частоту f0 на 10%. Пронаблюдайте временную диаграмму выходного сигнала резонатора. Повторите эксперимент, уменьшив резонансную частоту на 10%. Запишите в отчет вывод о влиянии расстройки резонатора на выходной сигнал. Для выполнения п.4 задания введите в программу Rezonator3 значение А2=1.1, не удовлетворяющее условию устойчивости. Остальные данные возьмите из таблицы 4. Примите f0=fc и запустите программу. Пронаблюдайте временную диаграмму выходного сигнала резонатора. Запишите максимальное значение абсолютной величины отсчета выходного сигнала при nmax=1000. Повторите эксперимент при nmax=10000. Приложение А к лабораторной работе №2 «Цифровой резонатор и его характеристики» АЧХ и ФЧХ резонатора На рисунке 1 приведено графическое представление алгоритма функционирования цифрового резонатора. 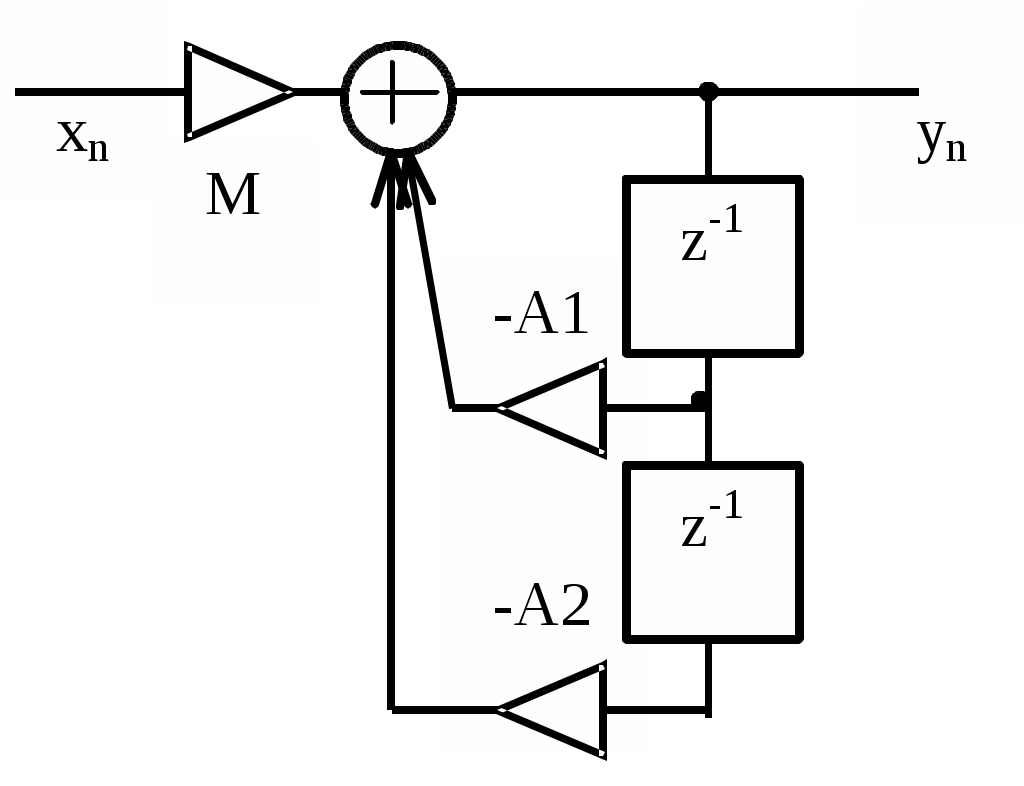 Рисунок 1-Цифровой резонатор Из него видно, что выходной сигнал резонатора определяется следующим соотношением  .Для определения системной функции резонатора сначала выразим Z-преобразование последовательности 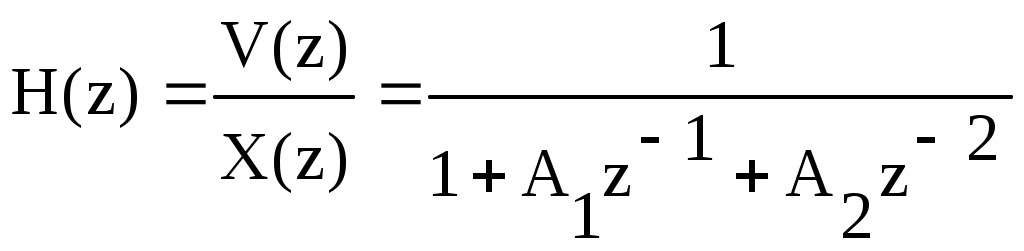 через Z - преобразование последовательности  , а затем найдем отношение  к   .Обозначим  и, используя подстановку  , получим выражение для комплексного коэффициента передачи .Модуль комплексного коэффициента передачи представляет собой АЧХ  , а аргумент – ФЧХ  резонатора .Для того чтобы выяснить влияние коэффициентов системной функции на АЧХ резонатора получим приближенную формулу для ее расчета. Представим выражение для системной функции в виде  , (1)где  и  - полюсы системной функции  .Для их определения знаменатель системной функции приравнивается нулю и находятся корни квадратного уравнения  при  .Комплексно-сопряженные полюсы системной функции резонатора представлены точками на комплексной плоскости 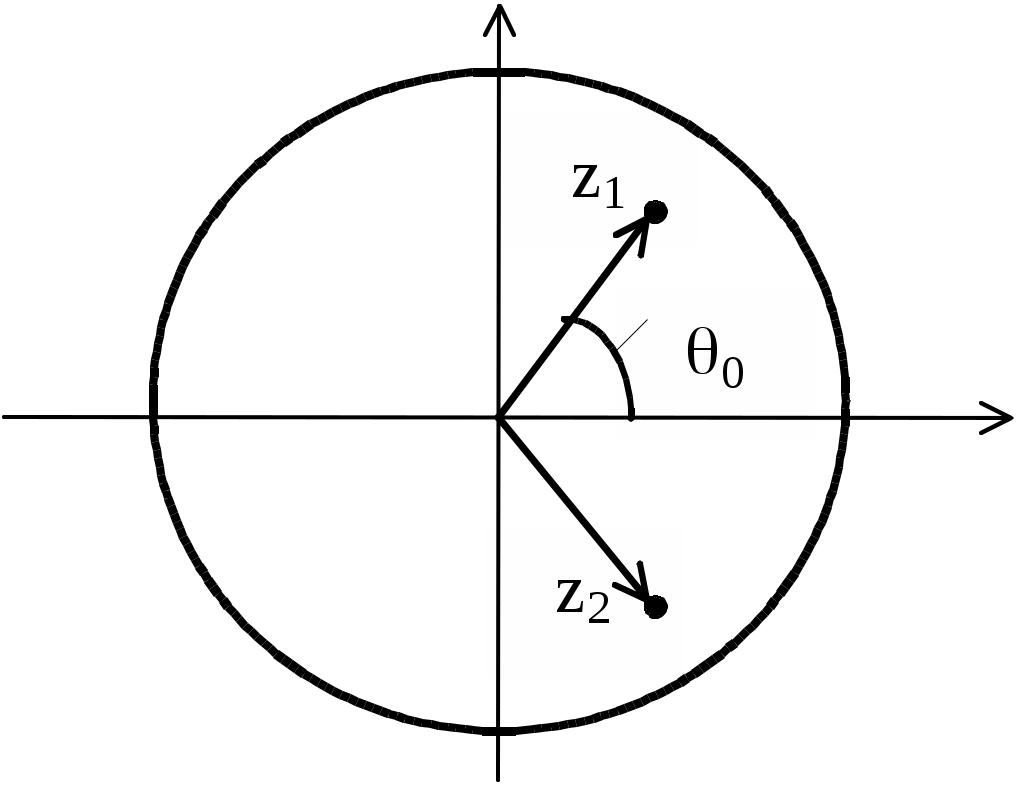 (рисунок 2). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||