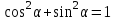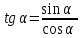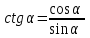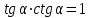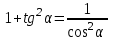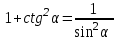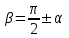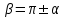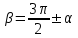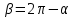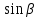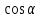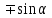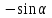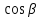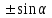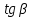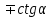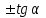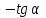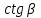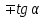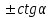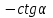Попова С.А. Конспект лекции Тригонометрия. Конспект лекций Тригонометрия. Конспект лекций по разделу Тригонометрия
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Основные тригонометрические тождества Тригонометрические функции связаны между собой следующими основными тождествами:
Из тождества I вытекают формулы 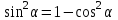 и и 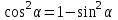 , которыми мы будем часто пользоваться. , которыми мы будем часто пользоваться.С помощью основных тригонометрических тождеств решается задача отыскания значений всех тригонометрических функций по известному значению одной из них. Формулы сложения аргументов 1. 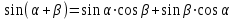 2. 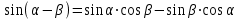 3. 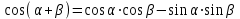 4. 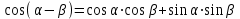 5. 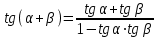 6. 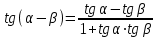 Формулы двойных и половинных углов Полагая 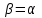 в формулах 1, 3, 5 сложения аргументов, получим следующие формулы двойных углов: в формулах 1, 3, 5 сложения аргументов, получим следующие формулы двойных углов:1. 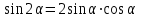 2. 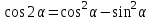 3. 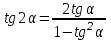 Из формулы 2 вытекают два часто употребляемых соотношения 4. 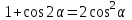 или или 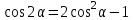 5. 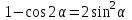 или или 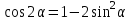 Из формул 4. и 5. можно получить формулы половинных углов: 6. 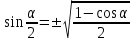 , , 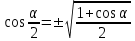 , , где знак зависит от четверти, в которой оканчивается угол /2. Заменяя в равенствах 1.- 3. 2 на , а на /2, находим: 7. 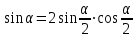 8. 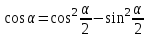 9. 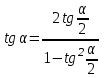 Кроме того, и выражаются через тангенс половинного угла по формулам 10. 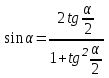 11. 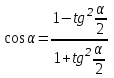 Формулы приведения Значения тригонометрических функций острых углов вычисляют по таблицам. Значения функций любых углов можно вычислить с помощью формул приведения к острому углу. Сформулируем общее правило написания формул приведения: Знак тригонометрической функции определяют по первоначально заданному углу. Если аргумент можно представить как сумму или разность , 2 и острого угла, то название функции не изменяют. Если аргумент можно представить как сумму или разность /2, 3/2 и острого угла, то название функции изменяют на сходное (синус – на косинус, тангенс – на котангенс).
Формулы сложения одноименных функций Формулы сложения одноименных тригонометрических функций позволяют преобразовать сумму и разность функций в произведение этих функций. Они имеют следующий вид: 1. 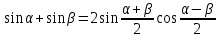 2. 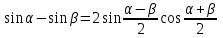 3. 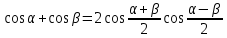 4. 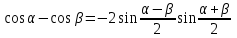 Как их получаем? Сложим соответственно левые и правые части формул сложения аргументов 1. и 2., введем новые переменные: 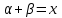 и и 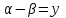 , тогда , тогда 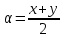 и и 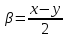 . . Т.е. 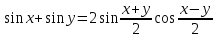 Теперь заменим 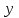 на на 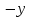 и получаем формулу сложения синусов: и получаем формулу сложения синусов: 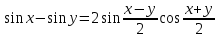 Аналогичные действия производим с формулами суммы и разности аргументов косинусов. Свойства и графики тригонометрических функций 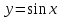 Область определения – множество всех действительных чисел. Область изменения (множество значений) – промежуток 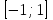 . .Функция 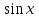 нечетная: нечетная: 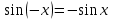 . .Функция 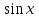 периодическая. Наименьший положительный период равен 2: периодическая. Наименьший положительный период равен 2: 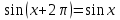 . .Нули функции: 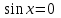 при при 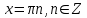 . .Промежутки знакопостоянства: 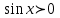 при при 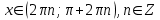 , ,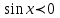 при при 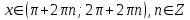 . .Функция 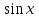 возрастает при 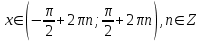 и убывает при 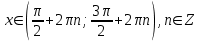 . .Функция 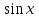 принимает принимает минимальные значения, равные -1, при 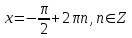 , , и максимальные значения, равные 1, при 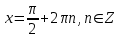 . .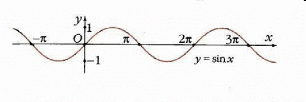 График функции 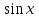 называют синусоидой. называют синусоидой.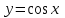 Область определения – множество всех действительных чисел. Область изменения (множество значений) – промежуток 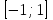 . .Функция 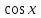 четная: четная: 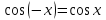 . .Функция 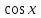 периодическая. Наименьший положительный период равен 2: периодическая. Наименьший положительный период равен 2: 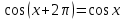 . .Нули функции: 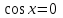 при при 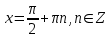 . .Промежутки знакопостоянства: 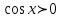 при при 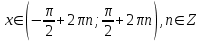 , ,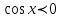 при при 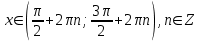 . .Функция 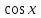 возрастает при 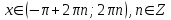 и убывает при 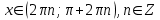 . .Функция 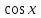 принимает принимает минимальные значения, равные -1, при 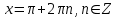 , , и максимальные значения, равные 1, при 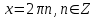 . .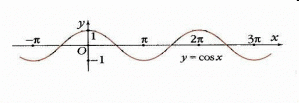 График функции 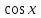 также называют синусоидой. также называют синусоидой.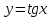 Область определения – множество всех действительных чисел, кроме чисел 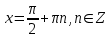 . .Область изменения (множество значений) – множество всех действительных чисел. Функция 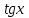 нечетная: нечетная: 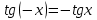 . .Функция 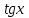 периодическая. Наименьший положительный период равен : периодическая. Наименьший положительный период равен : 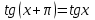 . .Нули функции: 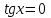 при при 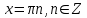 . .Промежутки знакопостоянства: 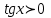 при при 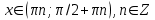 , ,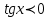 при при 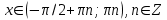 . .Функция 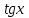 возрастает в каждом из промежутков возрастает в каждом из промежутков 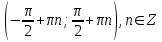 . .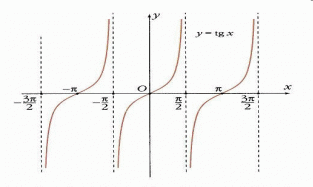 График функции 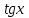 называют тангенсоидой. называют тангенсоидой.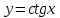 Область определения – множество всех действительных чисел, кроме чисел 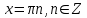 . .Область изменения (множество значений) – множество всех действительных чисел. Функция 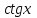 нечетная: нечетная: 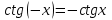 . .Функция 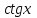 периодическая. Наименьший положительный период равен : периодическая. Наименьший положительный период равен : 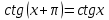 . .Нули функции: 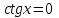 при при 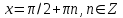 . .Промежутки знакопостоянства: 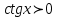 при при 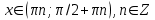 , ,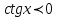 при при 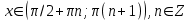 . .Функция 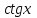 убывает в каждом из промежутков убывает в каждом из промежутков 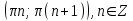 . .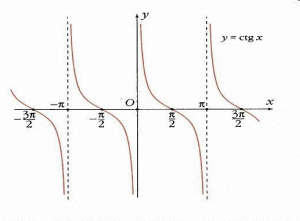 Обратные тригонометрические функции Теорема о корне П 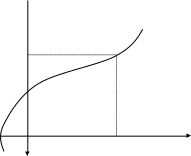 усть функция усть функция 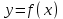 монотонна (возрастает или убывает) на промежутке I, число a – любое из значений, принимаемых f на этом промежутке. Тогда уравнение монотонна (возрастает или убывает) на промежутке I, число a – любое из значений, принимаемых f на этом промежутке. Тогда уравнение 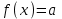 имеет единственный корень b в промежутке I. имеет единственный корень b в промежутке I.у y=f(x) a 0 bx Доказательство: Докажем единственность корня уравнения 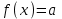 . .Пусть существует с – еще один корень уравнения 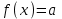 . .Т.е. 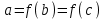 . . 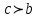 , либо , либо 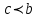 . .Т.к. 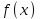 монотонна, то монотонна, то 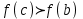 , либо , либо 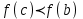 , что противоречит предположению. , что противоречит предположению.Следовательно, b - единственный корень. 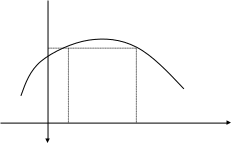 y y y=f(x) a 0 bcx Функция 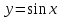 возрастает на отрезке возрастает на отрезке 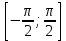 и принимает все значения от -1 до 1. Следовательно, по теореме о корне, для любого числа a, такого, что и принимает все значения от -1 до 1. Следовательно, по теореме о корне, для любого числа a, такого, что 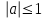 , в промежутке , в промежутке 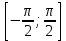 существует единственный корень bуравнения существует единственный корень bуравнения 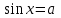 . Это число b называют арксинусом числа a и обозначают . Это число b называют арксинусом числа a и обозначают 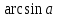 . .Арксинусом числа a называется число из отрезка 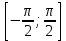 , синус которого равен a. , синус которого равен a. | |||||||||||||||||||||||||||||||