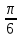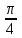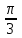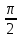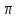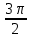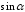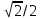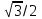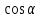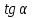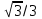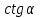Попова С.А. Конспект лекции Тригонометрия. Конспект лекций Тригонометрия. Конспект лекций по разделу Тригонометрия
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Конспект лекций по разделу «Тригонометрия»
Введение Тригонометрия возникла как аппарат для вычисления неизвестных параметров треугольника по заданным значениям других его параметров. Так, методами тригонометрии по данным сторонам треугольника можно вычислить его углы, по известной площади и двум углам вычислить стороны и т.д. Необходимость отыскивать неизвестные параметры данного треугольника впервые возникла в астрономии, и в течение долгого времени тригонометрия была одним из ее разделов. Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не рассматривали синусов, косинусов и тангенсов. Вместо таблиц этих величин они составили и использовали таблицы, позволяющие отыскивать хорду окружности по стягиваемой ею дуге. Дальнейшее развитие тригонометрия получила в средние века в работах индийских и арабских ученых. Современные буквенные обозначения появились в тригонометрии в середине XVIII века. Приблизительно в то же время в тригонометрии стала рассматриваться радианная мера угла, были введены тригонометрические и обратные тригонометрические функции числового аргумента, после чего тригонометрия приобрела свой современный вид. Тригонометрические функции числового аргумента, основные соотношения, знаки Радианная и градусная мера угла. Угол – часть плоскости, ограниченной двумя лучами, исходящими из одной точки, называемой вершиной угла. Рассмотрим новое определение угла. Пусть одна из сторон угла совпадает с положительным направлением оси Ох (луч l1), а вершина угла – с началом координат. На луче l2на расстоянии R=1 от начала возьмем точку А. Тогда при вращении луча l2 точка А опишет окружность с радиусом R=1, которую мы будем называть единичной окружностью (рис.1). Угол, полученный при повороте отрезка ОА, можно охарактеризовать двумя способами – радианной и градусной мерой. При градусном измерении за 10 принимается 1/360 полного угла. Тогда полный угол равен 3600, развернутый 1800, прямой угол 900. В радианной мере величина угла измеряется длиной соответствующей ему дуги. Например, величина полного угла равна длине окружности, т.е. в данном случае 2 (здесь =3,141596 – отношение длины окружности к диаметру. При вычислениях будем пользоваться значением 3,14), величина развернутого угла есть , величина прямого угла равна /2. Часто вместо записи величины угла в виде бесконечной десятичной дроби ее записывают в долях . Так, величину прямого угла записывают /2 вместо 1,57. Градусный и радианный способы измерения углов равноправны и используются достаточно широко. В некоторых случаях используют доли градуса – минуты и секунды. Минута – это 1/60 доля градуса и записывается так: 1=(1/60)0; секунда – это 1/60 доля минуты и записывается так: 1=(1/60) . Отметим, что при градусном измерении обозначения нужно обязательно записывать (знаки 0 , ,), а радианное обозначение всегда пропускают, записывая просто число радианов: 1; 0,75; 4,5; . Часто приходится переходить от градусного измерения к радианному и обратно. При этом используют следующие формулы:
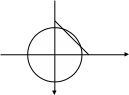
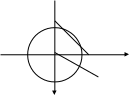
Луч l2единичной окружности можно вращать в двух направлениях: по часовой стрелке и против часовой стрелки. При движении l2 против часовой стрелки будем считать полученный угол положительным, а при движении этого луча по часовой стрелке – отрицательным (рис.2). При построении угла на единичной окружности луч l1 всегда совпадает с положительным направление оси Ох, а луч l2 вращается в соответствии с заданным условием. При этом луч l2 пересечется с единичной окружность в точке А (рис.3). Точка А , как всякая точка плоскости, имеет свои координаты (х;у).
Определение. Синусом угла называется ордината точки Апересечения подвижного луча и единичной окружности; косинусом угла называется абсцисса точки А; тангенсом угла называется отношение ординаты точки А к ее абсциссе; котангенсом угла называется отношение абсциссы точки А к ее ординате. Если угол оканчивается в четверти, то абсцисса и ордината точки А(х;у) являются длинами катетов прямоугольного треугольника с гипотенузой, равной 1. В этом случае определения тригонометрических функций угла совпадают с определением тригонометрических функций острого угла треугольника. Если угол оканчивается в любой другой четверти, то при нахождении значений тригонометрических функций необходимо учитывать знаки координат точки А(х;у). Знаки тригонометрических функций зависят от того, в какой четверти оканчивается заданный угол. Так как синусом называется ордината точки А, то синус положителен в I и II четвертях и отрицателен в III и IV четвертях (рис.4). Поскольку косинусом называется абсцисса точки А, косинус положителен в I и IV четвертях и отрицателен в II и III четвертях (рис.5). Так как тангенс угла есть отношение ординаты точки А к ее абсциссе, то тангенс положителен, когда знаки координат совпадают, и отрицателен, когда знаки координат различны (рис.6). Такие же знаки имеет и котангенс. Следовательно, тангенс и котангенс положительны в I и III четвертях и отрицательны в II и IV четвертях.
Значения тригонометрических функций некоторых углов приведены в следующей таблице:
Напомним понятия периодичности, четности и нечетности функций. Функция 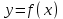 называется периодической, если существует такое число T (называемое периодом), что для всех выполняются равенства называется периодической, если существует такое число T (называемое периодом), что для всех выполняются равенства 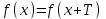 и и 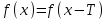 . Для построения графика периодической функции с периодом T достаточно провести построение на отрезке длиной T и затем полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси Ох. . Для построения графика периодической функции с периодом T достаточно провести построение на отрезке длиной T и затем полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси Ох.Все тригонометрические функции являются периодическими. Так как при вращении точки она, сделав полный оборот или несколько полных оборотов, займет первоначальное положение, ее координаты не изменяются. Следовательно, функции 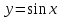 и и 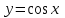 являются периодическими и их наименьший период равен 2 (3600), а функции являются периодическими и их наименьший период равен 2 (3600), а функции 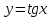 и и 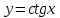 являются периодическими и их наименьший период равен (или 1800). являются периодическими и их наименьший период равен (или 1800). Итак, 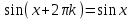 , , 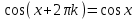 (k- целое неотрицательное число); (k- целое неотрицательное число); 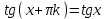 , , 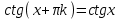 (k- целое неотрицательное число). (k- целое неотрицательное число).Вследствие того, что значение периодических функций не меняется от прибавления к аргументу целого числа периодов, для удобства вычислений можно добавлять или отбрасывать любое целое число периодов. Четной функцией называется функция, для которой при всех допустимых значениях аргумента выполняется равенство 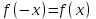 . Нечетной функцией называется функция, для которой при всех допустимых значениях аргумента выполняется равенство . Нечетной функцией называется функция, для которой при всех допустимых значениях аргумента выполняется равенство 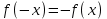 . График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат. . График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат.Среди тригонометрических функций имеется только одна четная 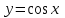 . Для нее справедливо равенство . Для нее справедливо равенство 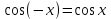 . Все остальные функции . Все остальные функции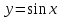 , , 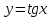 и и 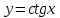 являются нечетными. Для них справедливы равенства являются нечетными. Для них справедливы равенства 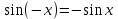 , , 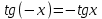 и и 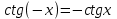 . . |

 y
y 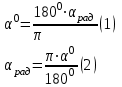
 y
y 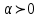
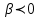
 y
y  наки синуса
наки синуса
 y
y