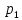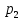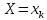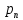питон2. Конспект лекций по теории вероятностей и математической статистике
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Конспект лекций по теории вероятностей и математической статистике. 3 семестр 2022/2023 учебный год. Лектор – Лохвицкий Михаил Сергеевич Часть 3 2. Случайные величины В жизни мы постоянно сталкиваемся с величинами, значения которых мы априорно не знаем (время ожидания транспорта, время безотказной работы аппаратуры, рост и вес человека в данный момент, курс акций на бирже, число студентов на лекции, продолжительность жизни любого субъекта). Всё это приводит нас к необходимости ввести в рассмотрение случайные величины. К случайным величинам относятся результаты измерений (из-за погрешностей измерительной аппаратуры), вычислений (из-за ошибок, возникающих при округлении и применении приближённых алгоритмов), параметры аппаратуры (из-за разного рода помех и геомагнитных воздействий) и т.п. Если значения, которые принимает случайная величина (СВ) дискретные или счетные ( 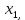 , ,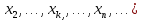 то СВ называется дискретной (ДСВ). В противном случае СВ называется непрерывной. то СВ называется дискретной (ДСВ). В противном случае СВ называется непрерывной.2.1. Дискретные случайные величины В результате опыта для ДСВ происходит событие 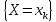 , а этому событию соответствует вероятность , а этому событию соответствует вероятность  . Соответствие между возможными значениями СВ и вероятностями их принятия называется законом распределения. Закон распределения можно задать в виде таблицы, которая называется рядом распределения: . Соответствие между возможными значениями СВ и вероятностями их принятия называется законом распределения. Закон распределения можно задать в виде таблицы, которая называется рядом распределения:
Совокупность событий 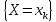 образует полную группу, поэтому выполняется следующее свойство: образует полную группу, поэтому выполняется следующее свойство:Свойство ряда распределения (условие нормировки) 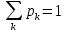 (2.1) (2.1) Закон распределения можно задать и графически. Такой график называется многоугольником распределения.                 0  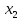  Рисунок. 2.2. Многоугольник распределения. Пример 2.1. На экзамене по Теории вероятностей студент может получить оценки 2, 3, 4, 5 с вероятностями 0,05; 0,15; 0,5; 0,3. Построить ряд и многоугольник распределения. Ряд распределения:
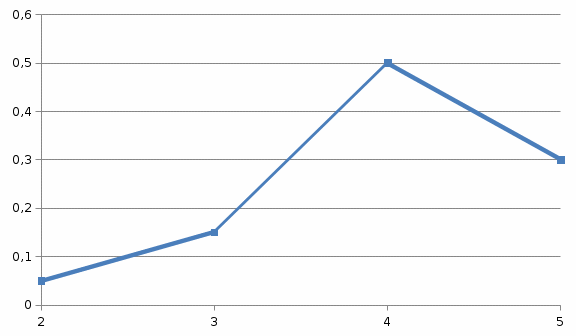 Рисунок 2.2. Многоугольник распределения СВ оценки на экзамене. 2.2. Функция распределения вероятностей Определение 2.2. Функция 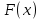 = Р (X < х), (2.2) = Р (X < х), (2.2)определенная при всех x  , называется функцией распределения вероятностей случайной величины X. , называется функцией распределения вероятностей случайной величины X.Свойства функции 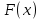 . . 1.  -неубывающая функция, т.е. если -неубывающая функция, т.е. если  , то , то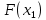 ≤ ≤ . Действительно, интервал . Действительно, интервал 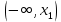 включен в интервал включен в интервал  поэтому вероятность попадания в меньший интервал (рисунок 2.3.) не может быть больше вероятности попадания в больший интервал: поэтому вероятность попадания в меньший интервал (рисунок 2.3.) не может быть больше вероятности попадания в больший интервал: 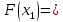 P(X< P(X<  ) )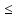 P(X < P(X < 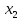 ) = ) =  2.  1. 1.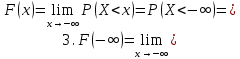 0 04. P( X ≥ x ) = 1 -  5. 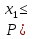 X X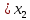 ) = ) = 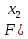 ) – F ( ) – F (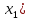 . (2.3) . (2.3)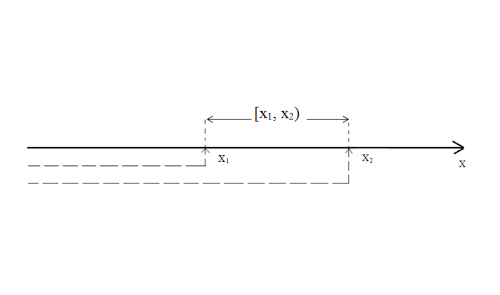 Рисунок 2.3. Вероятность попадания в интервал.. Событие попадания в интервал 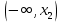 можно представить в виде суммы двух событий можно представить в виде суммы двух событий{X < 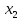 } = {X < } = {X <  } + { } + {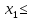 X X 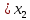 } }Т.к слагаемые в правой части - несовместные события, то P{X < 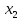 } = P{X < } = P{X <  } + P{ } + P{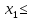 X X 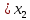 } }Заменяя первые две из этих вероятностей на выражение через функцию распределения, получаем требуемый результат. 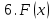 непрерывна слева, т.е. непрерывна слева, т.е.  . .Пример 2.2. Производятся наблюдения над состоянием определённого элемента технического устройства. Закон распределения
 Рис. 2.4. График 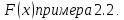  Если этот элемент включён в текущий процесс (состояние «on»), случайная величина Если этот элемент включён в текущий процесс (состояние «on»), случайная величина 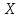 равна 1, если не включён (состояние «off»), то равна 1, если не включён (состояние «off»), то 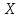 = 0. Пусть вероятность состояния «on» равна p = 0. Пусть вероятность состояния «on» равна p  (0;1), а состояния «off» q = 1-p. Найдем (0;1), а состояния «off» q = 1-p. Найдем 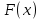 . Очевидно, что при всех x . Очевидно, что при всех x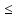 0 имеем P(X 0 имеем P(X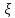 равно 0. равно 0.При 0 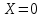 ) = q. При х>1 имеем: ) = q. При х>1 имеем:{ X 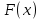 представлен на рисунке 2.4. Проведённый анализ позволяет обобщить результат на случай многих дискретных значений С.В. представлен на рисунке 2.4. Проведённый анализ позволяет обобщить результат на случай многих дискретных значений С.В. 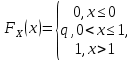 Пример 2.3. Случайная величина 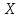 имеет распределение вида: имеет распределение вида:Р( 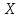 = = 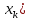 = =  , при некоторых значениях , при некоторых значениях  , ,  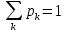 Это позволяет описать её в виде ряда распределения. Это позволяет описать её в виде ряда распределения.
В этом случае получаем для x 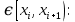 { X 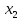 } + … + { X= } + … + { X=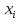 }, поэтому }, поэтому 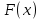 = = 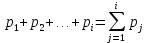 . .Окончательно получаем: 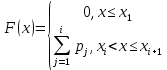 Если среди возможных значений случайной величины X имеется наибольшее, скажем, 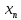 , то , то 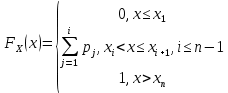 (2.4) (2.4)Графики функций распределения для бесконечной (а) и конечной (б) последовательностей  представлены на рис. 2.5. представлены на рис. 2.5.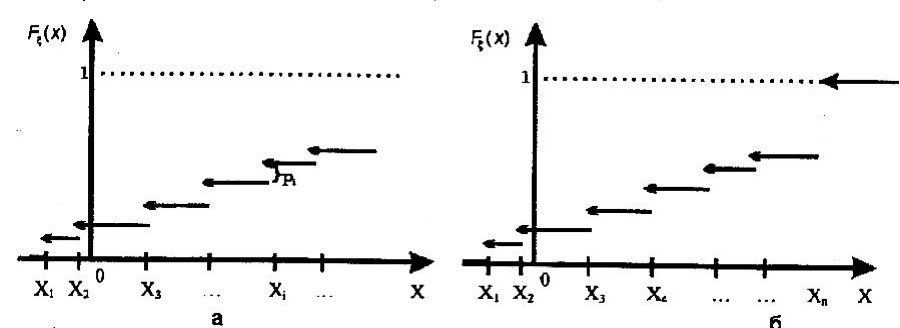 Рис. 2.5. Графики  примера 2.3.   Рис. 2.6. График  смешанной с.в. смешанной с.в.В общем случае по виду функции распределения случайные величины делятся на дискретные (  кусочнопостоянна), непрерывные ( кусочнопостоянна), непрерывные ( непрерывна) и смешанные. Пример графика непрерывна) и смешанные. Пример графика  для с.в. смешанного типа приведён на рис. 2.6. для с.в. смешанного типа приведён на рис. 2.6. 2.3. Плотность распределения вероятностей Определение 2.3. Если  непрерывна и дифференцируема, то её производная непрерывна и дифференцируема, то её производная (2.5) (2.5)называется плотностью распределения с.в. X. Свойства плотности распределения: 1.  2. 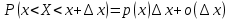 Доказательство: 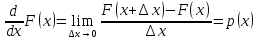 по теореме из теории пределов получим равенство по теореме из теории пределов получим равенство 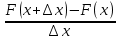 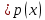 + +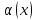 , где , где 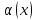 - бесконечно малая. Умножим обе части последнего равенства на - бесконечно малая. Умножим обе части последнего равенства на 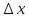 , а приращение функции распределения (по свойству 5) заменим на вероятность попадания в интервал , а приращение функции распределения (по свойству 5) заменим на вероятность попадания в интервал 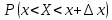 . В итоге получается равенство, которое мы хотели доказать (свойство 2 плотности). . В итоге получается равенство, которое мы хотели доказать (свойство 2 плотности).3. 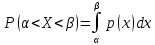 (2.6) (2.6)Доказательство: интервал 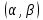 разобьем на части разобьем на части 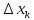 , вероятность попадания в каждый интервалов определим по формуле из предыдущего свойства. Затем max , вероятность попадания в каждый интервалов определим по формуле из предыдущего свойства. Затем max 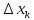 устремим к нулю. Предел интегральных сумм и будет интеграл устремим к нулю. Предел интегральных сумм и будет интеграл 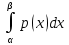 : :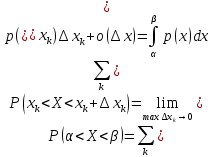 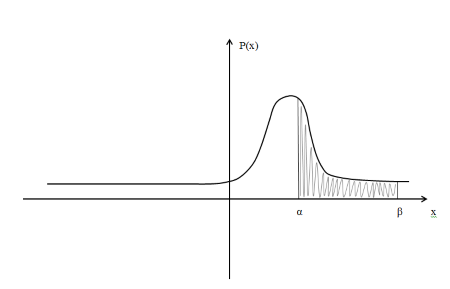  Т.е. вероятность попадания в интервал  численно равна площади под графиком плотности на этом интервале (рисунок 2.7). численно равна площади под графиком плотности на этом интервале (рисунок 2.7). 4.  (2.7) (2.7)Доказательство: используем предыдущее свойство при  и и  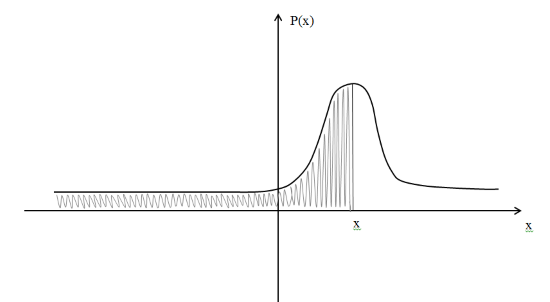 Рисунок 2.8. Связь функции распределения с плотностью. Геометрически  численно равна площади под графиком функции численно равна площади под графиком функции 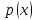 , лежащей левее абсциссы х (заштрихованная область на рис. 2.8). , лежащей левее абсциссы х (заштрихованная область на рис. 2.8).5.  6.  (условие нормировки) (2.8) (условие нормировки) (2.8)Условие нормировки: график  всегда ограничивает площадь, равную 1 (рисунок 2.9.) всегда ограничивает площадь, равную 1 (рисунок 2.9.)Доказательство: используем свойство 3 при  и и  Вероятность, стоящая в левой части равенства из свойства 3, в этом случае стремится к 1. Вероятность, стоящая в левой части равенства из свойства 3, в этом случае стремится к 1.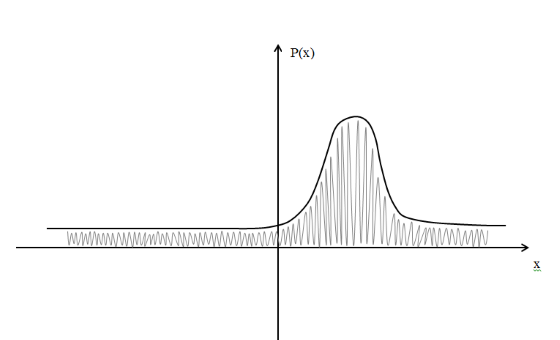 Рисунок 2.9. Условие нормировки плотности. 2.3. Числовые характеристики случайных величин Закон распределения (ряд распределения или многоугольник) для ДСВ, функция распределения как для дискретной, так и для непрерывной СВ, плотность распределения для непрерывной СВ являются самыми полными характеристиками СВ. Однако, во многих задачах можно ограничиться только несколькими числовыми характеристиками такими как, например, среднее ожидаемое значение, среднее отклонение от этого среднего значения и т.д. 2.3.1. Математическое ожидание Пример 2.4. В результате n испытаний СВ приняла значение x1 - n1 раз, значение x2 - n2 раза,…, значение xk -nk раз. В математической статистике значения, которые принимает СВ называются выборкой, а n – объёмом выборки: 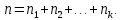 Найдём среднее арифметическое всех полученных значений. Оно называется средним выборочным значением и обозначается Найдём среднее арифметическое всех полученных значений. Оно называется средним выборочным значением и обозначается 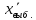 : :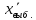 = =  = = 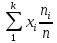 (2.9) (2.9)Но величина 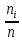 это относительная частота появления события это относительная частота появления события 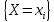 , которая является оценкой вероятности этого события. Поэтому средним ожидаемым значениям СВ по определению является следующая величина: , которая является оценкой вероятности этого события. Поэтому средним ожидаемым значениям СВ по определению является следующая величина:Определение. 2.4. Математическим ожиданием ДСВ называется величина: 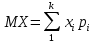 . (2.10) . (2.10)Определение .2.5. Математическим ожиданием непрерывной СВ называется величина: 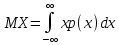 (2.11) (2.11)Замечание. В дальнейшем будем считать, если есть выражение 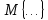 , то это значит вычисляется среднее значение для , то это значит вычисляется среднее значение для 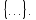 Свойства математического ожидания 1.MC =C; (2.12) Т.е. математическое ожидание постоянной равно самой этой постоянной. Доказательство: можно считать, что в этом случае СВ принимает только одно значение С с вероятностью единица. МС=С  2. M (CX) =C МX ; (2.13) Таким образом, постоянную можно выносить за знак математического ожидания (за знак усреднения). Доказательство: Если случайная величина X принимает значение 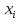 , то СX принимает значение , то СX принимает значение 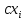 с вероятностью с вероятностью  . Поэтому . Поэтому  3. М(X +Y ) = МX + МY; (2.14) 4. Если случайные величины независимы , то М(XY ) = МX МY. (2.15) Замечание. Определение независимости СВ будет дано через несколько лекций, там же будет и доказано это свойство. Пример 2.4 Рассмотрим две случайные величины X и Y со следующими законами распределения
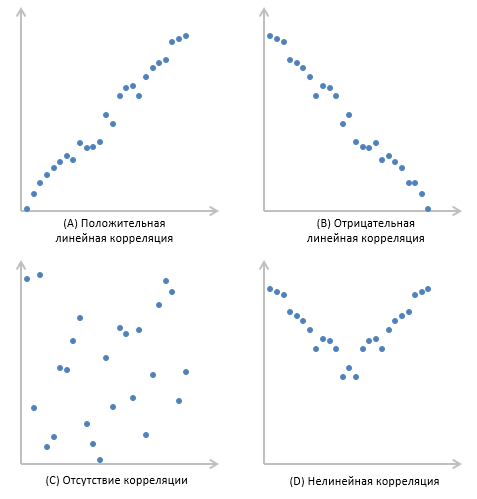
Найти математические ожидания случайных величин X и Y. Решение: MX = -1  0,5 + 1 0,5 + 1  0,5=0; MY = -1 0,5=0; MY = -1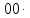 0,5 + 100 0,5 + 100  0,5=0. 0,5=0.Вывод: Математические ожидания у этих величин равны, но из законов распределения видно насколько эти величины различны. В теории вероятностей вводятся характеристики, которые характеризуют средние отклонения (разброс) СВ от их средних значений. Это дисперсия и среднее квадратическое отклонение. 2.3.2. Дисперсия и среднее квадратическое отклонение Определение. 2.6. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от математического ожидания: DX = M (X – MX) 2(2.16) Вероятностный смысл дисперсии: Дисперсия равна среднему значению квадрата разброса случайной величины от её математического ожидания. Поэтому вводят определениесреднего квадратического отклонения:  (2.17) (2.17)Эта величина характеризует среднее отклонение СВ от математического ожидания. Формула для вычисления дисперсии дискретной случайной величины: DX =  (2.18) (2.18)Формула для вычисления дисперсии непрерывной случайной величины: DX = 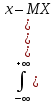 (2.19) (2.19)Замечание. С целью сокращения числа вычислений дисперсию чаще вычисляют по вычислительной формуле: Вычислительная формула для дисперсии: 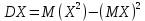 . (2.20) . (2.20) Вывод формулы: 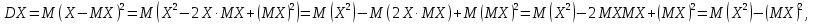 Величина  вычисляется по следующим формулам: вычисляется по следующим формулам: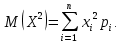 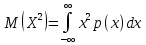 , (2.21) , (2.21)для дискретной и непрерывной СВ соответственно. Свойства дисперсии Дисперсия постоянной величины равна нулю: 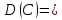 0 (2.22) 0 (2.22)Доказательство.  Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 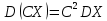 (2.23) (2.23)Доказательство. 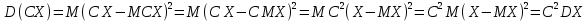 Если случайные величины X и Y независимы, то: 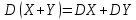 (2.24) (2.24)Замечание. Определение независимости СВ будет дано через несколько лекций, там же будет и доказано это свойство. Следствие 1.  DX DXСледствие 2. 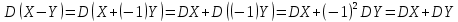 . (для независимых X,Y) . (для независимых X,Y)Свойства среднеквадратического отклонения:  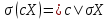 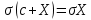 Достоинством 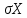 является тот факт, что оно имеет ту же размерность, что и X. является тот факт, что оно имеет ту же размерность, что и X. Нормальное (гауссовское) распределение 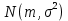 Плотность распределения нормального закона имеет вид  (3.1) (3.1)Наиболее часто встречается во всех областях науки и техники, экономики и финансов, медицине и демографии. Например, величина помехи в радиоканале, ошибки в любых измерениях, коэффициент интеллектуальности (IQ), рост человека, изменение напряжения в сети, колебания курса акций, температура тела, возраст въезжающих в страну эмигрантов имеют нормальное распределение (разумеется, в каждом случае значения параметров 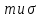 меняются). Важность этого закона следует из Центральной предельной теоремы. На качественном уровне ЦПТ утверждает, что при определенных условиях (достаточно часто выполненных на практике) сумма случайных величин имеет асимптотически нормальное распределение независимо от того, каково было первоначальное распределение отдельных слагаемых. меняются). Важность этого закона следует из Центральной предельной теоремы. На качественном уровне ЦПТ утверждает, что при определенных условиях (достаточно часто выполненных на практике) сумма случайных величин имеет асимптотически нормальное распределение независимо от того, каково было первоначальное распределение отдельных слагаемых.Параметры:  Неприятной неожиданностью является тот факт, что функция распределения такой с. в. 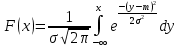 аналитически явно не выражается. Поэтому для практического использования нормального распределения приходится прибегать к таблицам или специальным вычислительным процедурам для нахождения значений функции аналитически явно не выражается. Поэтому для практического использования нормального распределения приходится прибегать к таблицам или специальным вычислительным процедурам для нахождения значений функции 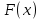 . При этом нет необходимости составлять таблицы для каждой пары параметров . При этом нет необходимости составлять таблицы для каждой пары параметров  , а достаточно обойтись таблицами для m = 0 и , а достаточно обойтись таблицами для m = 0 и 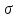 = 1 (соответствующее распределение ещё называют стандартным нормальным распределением). Плотность распределения этого закона = 1 (соответствующее распределение ещё называют стандартным нормальным распределением). Плотность распределения этого закона 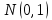 обозначается, как обозначается, как  . Функция распределения этого закона имеет вид . Функция распределения этого закона имеет вид 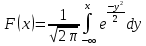 . . (в последнем интеграле мы поменяли местами пределы интегрирования, изменив знак перед интегралом). ВАЖНАЯ ФОРМУЛА. Вероятность попадания в интервал для нормально распределённой С.В.: 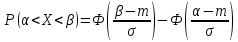 (3.2) (3.2)Где 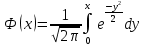 - функция Лапласа. (3.3) - функция Лапласа. (3.3)(Напомним, что функция Лапласа – нечетная и при 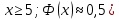 Следствия из формулы (32): Функция распределения равна  (было использовано. что (было использовано. что 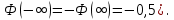 Формула вероятности попадания в интервал, симметричный относительно математического ожидания. 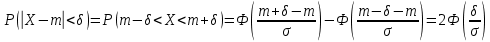 (3.4) (3.4)(было использовано свойство нечетности функции Лапласа). «Правило» трёх сигм. При  из предыдущей формулы получим из предыдущей формулы получим 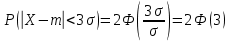 = 2 = 2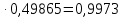 Т.е. с вероятностью близкой к 1 почти все значения нормального закона 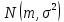 принимают значения в интервале с радиусом принимают значения в интервале с радиусом  и центром в точке и центром в точке  В обозначении 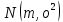 первый параметр равен математическому ожиданию, а второй параметр равен дисперсии с.в. первый параметр равен математическому ожиданию, а второй параметр равен дисперсии с.в.Определение 6.2. Коэффициентом корреляции двух с. в. X и Y называется число 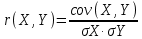 . (3.5) . (3.5)где 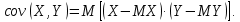 (3.6) (3.6)Замечание. По аналогии с моментами одной с. в. ковариацию можно назвать смешанным центральным моментом второго порядка. Вычислительная формула для ковариации. 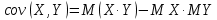 Свойства коэффициента корреляции: 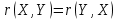 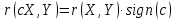 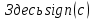 = = 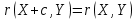 | 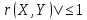 Если X и Y независимы, то 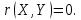 Если Y=kX+b, то 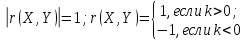 Из свойства 6 ковариации, в частности вытекает, что если две гауссовские случайные величины независимы, то 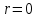 . Верно и обратное: если . Верно и обратное: если 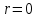 , то две гауссовские с.в. независимы (докажите это). Но в общем случае из некоррелированности случайных величин (т. е. из того, что cov(X, Y) = 0) не следует их независимость. , то две гауссовские с.в. независимы (докажите это). Но в общем случае из некоррелированности случайных величин (т. е. из того, что cov(X, Y) = 0) не следует их независимость.Чем лучше реальная зависимость Y от X аппроксимируется линейной, тем ближе по модулю к 1 будет их коэффициент корреляции. Если 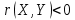 это означает, что с ростом одной величины другая имеет тенденцию убывать. это означает, что с ростом одной величины другая имеет тенденцию убывать.Если 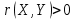 это означает, что с ростом одной величины другая имеет тенденцию возрастать. это означает, что с ростом одной величины другая имеет тенденцию возрастать.Шкала Чеддока для оценки линейной связи двух случайных величин
 ЗАКОН БОЛЬШИХ ЧИСЕЛ, Утверждение теоремы Чебышева означает, что при выполнении определённых условий среднее арифметическое случайных величин в первом приближении сходится к среднему арифметическому их математических ожиданий, т.е. случайные величины  при при 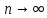 сходятся по вероятности к сходятся по вероятности к 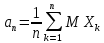 . . |