ТВиМС. Конспект ТВ ч.1. Конспект лекций по теории вероятностей и математической статистике
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
Конспект лекций по теории вероятностей и математической статистике. Авторы: Лохвицкий М.С., Синева И.С. 4 семестр 2020/2021 учебный год. Лектор – Лохвицкий Михаил Сергеевич События и вероятность События. Основные определения. Определение 1.1. Событие - любой исход опыта, который может произойти или не произойти. Определение 1.2 Элементарными событиями называются неразложимые и взаимоисключающие исходы опыта. Определение 1.3 Событие наз. достоверным, если при данных условиях оно обязательно наступит. Обозначение события: Ω. Определение 1.4 Событие наз. невозможным, если при данных условиях оно наступить не может. Обозначение Ø. Определение 1.5 Два события наз. несовместными, если в одном опыте они не могут произойти вместе. Определение 1.6. Несколько событий образуют полную группу, если они попарно несовместны и в результате каждого опыта происходит одно и только одно из них. Определение 1.7. Несколько событий наз. равновозможными, если из условий симметрии нет оснований считать, что ни одно из них является более возможным. Определение 1.8. Суммой событий А и В называется событие С=А+В, состоящее в наступлении хотя бы одного из них (т.е. или А, или В, или А и В вместе). Определение 1.9. Произведением событий А и В называется событие С=АВ, состоящее в наступлении двух событий (т.е. А и В вместе). Определение 1.10. Противоположным событию А (отрицание события А) называется событие Ā, происходящее тогда и только тогда, когда А не происходит. Геометрическая интерпретация операций над событиями показана в следующей таблице:
Свойства: А+В =В+А АВ =ВА (A+ B) C= AC +BC Леммы де Моргана 4.  = =   Решить задачи 1.1. (Ответы выбрать из следующих: А, Ā, Ω, Ø). А+А = АА = А+ Ω = А Ω = А Ø = А+ Ø= А+ Ā = А Ā = Ø̅ = 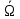 = =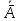 = =Вероятность Определение 1.11. Вероятность – число, характеризующее степень возможности события: Р(Ω)=1; Р(Ø)=0: 0≤ Р(А) ≤1 Оценкой вероятности является относительная частота появления события в большом числе испытаний: 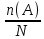 (1.1) (1.1)Где  число появлений события А в N испытаниях. число появлений события А в N испытаниях. 1.12.Классическое определение вероятности. Если исходы опыта образуют полную группу несовместных равновозможных событий, то вероятность вычисляется по формуле Р(А)= 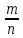 (1.2) (1.2)Где n – общее число возможных исходов опыта, m – число исходов опыта, в которых происходит событие А. Задачи на классическое определение вероятности. Пример 1. 1. Подбрасываем правильную монетку: а. Событие Г= 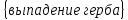 ; Ц = ; Ц = . .P( Г) = 1/2; P( Ц ) = 1/2 б. Монетку подбрасываем два раза. Определить вероятности событий А=  , Б = , Б = , ,В =  , ,Возможные исходы опыта: ГГ; ГЦ; ЦГ; ЦЦ. P( А ) = 3/4; P( Б ) = 2/4 = 1/2; P( В ) = 1/4. Пример 1.2. Игральная кость ( цифры 1 – 6). а. Событие А =  , ,P( А ) = 1/6; b. Событие Б=  , ,P( Б ) = 3/6 = 1/2; Пример 1.3. Колода из 36 карт. Из колоды вынимают одну карту. Найти вероятности: а). вытянуть даму пик; б). вытянуть туз; в). вытянуть карту пиковой масти. Определение 1.13. Сочетаниями из n элементов по k называются группы по kэлементов, взятых из данных n элементов, и отличающиеся друг от друга хотя бы одним элементом. Число сочетаний определяется по формулам: 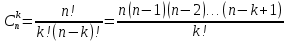 (1.3) (1.3)Полезное свойство: 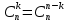 (1.4) (1.4)Пример 1.4..  Определение. Перестановками изnэлементов называются группы по n элементов, и отличающиеся друг от друга порядком хотя бы двух элементов. Число перестановок определяется по формуле: 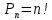 Определение 1.14. Размещениями из n элементов по k называются группы по kэлементов, взятых из данных n элементов, и отличающиеся друг от друга хотя бы одним элементом или порядком элементов Число размещений определяется по формулам:  (1.5) (1.5)Пример 1.5. В группе 30 человек, из них 20 юношей и 10 девушек. Преподаватель вызывает к доске двух человек из списка студентов случайным образом. Какова вероятность, что это а) юноши, б) девушки, в) юноша и девушка. Решение. Общее число возможных исходов 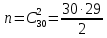 =435; a) =435; a)  =190 ; =190 ;  ; ;б) 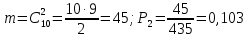 ; ; в)  . .Замечание. Число m в пункте в) можно было вычислить иначе: 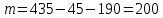 . .Задача 1.2. Спортлото, выбираются 6 цифр из 49. Какова вероятность а) максимального выигрыша (угадать все 6 цифр): б) угадать 5 цифр из 6: в) угадать 4 цифры из 6. Аксиоматика теории вероятностей Определение 1.15. Множество Ω={ 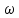 } всех возможных исходов данного опыта (наблюдения, эксперимента) называется пространством элементарных событий, а сами исходы } всех возможных исходов данного опыта (наблюдения, эксперимента) называется пространством элементарных событий, а сами исходы 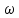 - элементарными событиями. - элементарными событиями.В примере 1.1б: Ω={ГГ, ГЦ, ЦГ, ЦЦ}. В примере 1.5. Ω={все возможные пары студентов }, Пример 1.6. В соревнованиях по биатлону фиксируется время t, за которое спортсмен прошёл дистанцию, и количество попаданий (или наоборот - промахов) при стрельбе n раз. Тогда Ω ={ 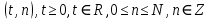 }. }.На пространстве Ω вводится специальное множество U «допустимых» подмножеств, которое называется - сигма алгеброй (  -алгебра). -алгебра).Определение 1.16. Множество U подмножеств пространства Ω образует  - алгебру, если: - алгебру, если: 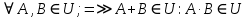 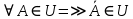  ….., ….., Замечание. Алгебра (расширенная арифметика ) изучает операции над элементами множеств произвольной природы . В целом задача определения, является ли данное множество подмножеств  - алгеброй, часто является достаточно сложной. Но если удаётся такую алгебру построить, то далее все вероятностные вычисления корректны. - алгеброй, часто является достаточно сложной. Но если удаётся такую алгебру построить, то далее все вероятностные вычисления корректны. Определение 1.17. Пара (Ω, ∪), состоящая из пространства Ω и введённой на нём  - алгебры U, называется измеримым пространством. - алгебры U, называется измеримым пространством.Определение 1.18. Тройка (Ω, U, Р) называется вероятностным пространством, если (Ω, U) образуют измеримое пространство, а Р - функция на нём, называемая вероятностью и удовлетворяющая следующим условиям: P(Ω)=1 (нормированность) 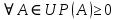 (неотрицательность) (неотрицательность) (аддитивность) (аддитивность)  …, …, 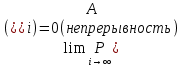 Замечания. Условия 1-3 в определении 1.16 и условия 1-4 в определении 1.18 называются аксиомами. Свойства вероятности Свойство 1. 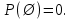 Действительно, в силу аксиомы 3 определения 1.18:  , поэтому P(Ø) = 0. , поэтому P(Ø) = 0.Свойство 2. 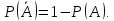 Из определения противоположного события и аксиом 1 и 3 определения 1.18 следует, что 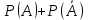 =1 =1Свойство 3.  Свойство 4. Если события 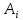 попарно несовместны, то попарно несовместны, то P ( 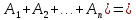 P( P(  P( P( 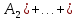 P( P( 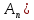 Свойство 5. Теорема сложения 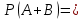 Р(А) + Р(В) - Р(АB) (1.6) Р(А) + Р(В) - Р(АB) (1.6)Так как 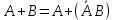 и события A и  несовместные, то по аксиоме 3 из определения 1.18 несовместные, то по аксиоме 3 из определения 1.18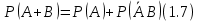 Из равенств  следует, что  подставив последнее равенство в равенство 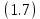 получим теорему сложения (1.6) (свойство 5). получим теорему сложения (1.6) (свойство 5).Замечание. В частном случае несовместных событий А и В из теоремы сложения получаем аксиому 3 из определения 1.18. 1.5.Условные вероятности Определение 1.19. Условной вероятностью события A при условии, что произошло событие B, называется P(А/B) = 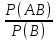 (1.8) (1.8)Замечание.Здесь и в дальнейшем вероятности, стоящие в знаменателе, не равны нулю. Задача 1.3. В классической схеме общее число исходов опыта равно n. Из них m исходов благоприятны событию А, k исходов опыта благоприятны В, e исходов благоприятны и А и В (т.е. благоприятны АВ). Запишите выражения для вероятностей  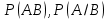 . Покажите, что равенство (1.3) для классического определения вероятности выполняется. . Покажите, что равенство (1.3) для классического определения вероятности выполняется. 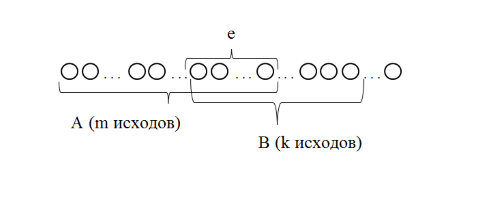 Рисунок.1.1. Схема к задаче 1.3. Общее число исходов опыта n. Замечание. Задача 1.3. показывает, что для классической схемы условная вероятность вычисляется по формуле (1.8), и эта формула по определению 1.19 обобщается на любые события. Следствие 1. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго события, вычисленную при условии, что первое событие произошло:  Р(В/А) = Р(В) Р(В/А) = Р(В)  Р(А/B). (1.9) Р(А/B). (1.9)Следствие 2. Для трёх событий:  Р(А) Р(А) Р(В/А) Р(В/А) Р(С/АВ) (1.10) Р(С/АВ) (1.10)Т.е. вероятность произведения событий равна вероятности одного из них, умноженную на вероятность второго события, вычисленную при условии, что первое событие произошло, умноженную на вероятность третьего события, вычисленную при условии, что первые два события произошли. Замечание. Аналогичные формулы верны для n событий. Пример 1.7. Рассматриваются 4 кубика, на которых изображены буквы М, М, А, А. Кубики случайным образом вкладывают в коробку в линию. Какова вероятность, что получится слово «МАМА». Решение.  P(A/MAM) = P(A/MAM) =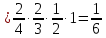 Определение 1.20.. Два события называются независимыми, если появление одного из них не меняет вероятность другого, т.е. Р(А/B) = Р(А) и Р(В/А) = Р(В) (1.11) (Т.е. условная вероятность равна безусловной). Задача 1.4. Показать, что если Р(А)>0, P(B)>0 и А не зависит от В, то В не зависит от А. Теорема умножения для независимых событий. Вероятность произведения независимых событий равна произведению их вероятностей: 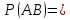 Р(А) Р(В) (1.12) Р(А) Р(В) (1.12)Задача 1.5. Докажите, что, если для событий А и В выполняется равенство (1.6) , то эти события независимы. (Следовательно, это равенство можно принять за эквивалентное определение независимости событий). Теорема сложения для совместных независимых событий. 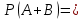 Р(А) + Р(В) – Р(А) Р(В) (1.13) Р(А) + Р(В) – Р(А) Р(В) (1.13)Доказательство. Подставив (1.12) в формулу (1.6) получим теорему (1.13). Пример 1.8. В колоде 36 карт, по 9 карт каждой масти. Событие А состоит в том, что наудачу вытянутая карта – король; событие В – в том, что она трефовой масти. Тогда исходя из равновозможности вынуть любую карту из колоды получаем: 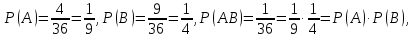 т.е. события А и В независимы. т.е. события А и В независимы. Добавим в колоду ещё одну специальную карту - «джокера», который может заменить собой любую нужную карту, и подсчитаем вероятности:  т.е. теперь события А и В оказались зависимыми. т.е. теперь события А и В оказались зависимыми.Определение 1.21. События  , ,  ,…, ,…,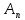 называются независимыми в совокупности, если называются независимыми в совокупности, если 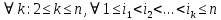 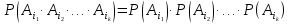 (1.14) (1.14)Это определение означает, что независимы любые пары, тройки и т.д. событий. Обратите внимание на тот факт, что из попарной независимости событий не следует их независимость в совокупности, что наглядно иллюстрирует следующий пример. Пример 1.9 . На координатной плоскости наудачу ставится точка. А = {точка находится в верхней полуплоскости}, B = {точка находится в правой полуплоскости}, С = {знаки абсциссы и ординаты точки одинаковы}, Тогда 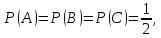 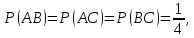 но P(ABC)=P(точка лежит в первом квадранте) = но P(ABC)=P(точка лежит в первом квадранте) =  и и 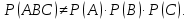 Хотя события A, Bи Cпопарно независимы, они зависимы в совокупности, поскольку в данном случае наступление любых двух из них автоматически влечёт за собой наступление третьего. Обратите внимание на решение следующего типа задач: задачи на «Цепочки». Пример 1.10. Отдельные элементы (i) каждого блока предложенных ниже схем выходят из строя в течение определенного периода времени независимо от остальных с вероятностями pi. При выходе из строя блока соединение в этом месте нарушается. Найти вероятность обрыва соединения за этот период для каждой из схем.  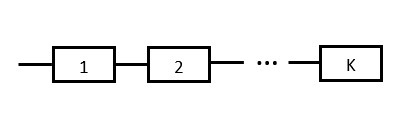 Рисунок. 1.2.а Рисунок.1.2.б  Рисунок.1.2.в 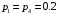 , , 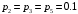 . .Определение 1.22. Надежностью работы устройства за время Т называется вероятность безотказной работы за это время. Безотказная работа и выход из строя – события противоположные. Решение. Пусть событие 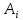 состоит в отказе элемента с номером состоит в отказе элемента с номером 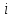 за рассматриваемый промежуток времени. Тогда за рассматриваемый промежуток времени. Тогда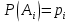 , Событие , Событие 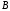 соответствует обрыву соединения за то же время. соответствует обрыву соединения за то же время. 1.10.а. Для соединения на рисунок 1.2.а обрыв соответствует тому, что будут оборваны все ветви, поэтому  . В силу независимости отказов отдельных элементов . В силу независимости отказов отдельных элементов  . .Замечание. Все вероятности в предыдущей формуле меньше 1, поэтому вероятность обрыва соединения при параллельном соединении (это называется горячим резервированием) меньше, чем самая маленькая вероятность 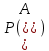 (самый надежный элемент). Поэтому надежность при горячем резервировании больше, чем надежность самого лучшего (надежного) элемента. (самый надежный элемент). Поэтому надежность при горячем резервировании больше, чем надежность самого лучшего (надежного) элемента.1.10.б Для соединения на рисунке 1.2.б обрыв происходит, если откажет хотя бы один элемент, поэтому 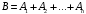 . .Рекомендация. Вычисление вероятности суммы трёх и болеесовместных событий всегда рациональнее вычислять переходом к противоположному событию. В данной задаче противоположное событие это - прохождению сигнала через все элементы схемы 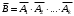 получаем получаем  Замечание. Здесь 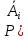 ) надежность i-го блока, поэтому надежность всего устройства ) надежность i-го блока, поэтому надежность всего устройства 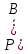 при последовательном соединении хуже (меньше), чем надежность самого ненадежного блока. при последовательном соединении хуже (меньше), чем надежность самого ненадежного блока.Соответственно, 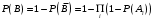 . .Перейдем к решению задачи со схемой рисунка 1.2.в. 1.10.в. Обозначим событие, состоящее в отказе блока параллельно соединенных элементов (все отказали) 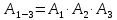 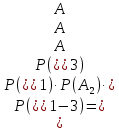 =0.2 =0.2 Тогда 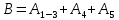 . Переходим к противоположному событию (сигнал проходит и через блок параллельных элементов и блоки 4 и 5). . Переходим к противоположному событию (сигнал проходит и через блок параллельных элементов и блоки 4 и 5). = =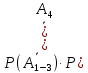 =0.998 =0.998 тогда для вероятности обрыва соединения получаем 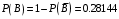 . .Пример 1.11. Пакет информации может поступить независимо от трёх источников с вероятностями 0.7, 0.8 и 0.9 соответственно. Найти вероятность того, что пакет информации поступит: а) только от одного источника; б) хотя бы от одного источника. Решение. а) Введем события  {пакет информации от i-го источника поступил}, i = 1, 2, 3. Тогда по условию {пакет информации от i-го источника поступил}, i = 1, 2, 3. Тогда по условию 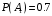 , , 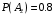 , ,  . Пусть В = { пакет информации поступил только от одного источника }, C = {пакет информации поступил хотя бы от одного источника }. Наступление события В означает, что реализовался один и только один из следующих сценариев: 1) пакет информации принят от первого источника, но не принят от второго и третьего (т.е. произведение этих трёх событий); 2) пакет информации принят от второго источника, но не принят от первого и третьего; 3) пакет информации принят от третьего источника, но не принят от первого и второго. На языке алгебры событий (или первый сценарий, или второй, или третий – т.е. сумма событий) это означает, что . Пусть В = { пакет информации поступил только от одного источника }, C = {пакет информации поступил хотя бы от одного источника }. Наступление события В означает, что реализовался один и только один из следующих сценариев: 1) пакет информации принят от первого источника, но не принят от второго и третьего (т.е. произведение этих трёх событий); 2) пакет информации принят от второго источника, но не принят от первого и третьего; 3) пакет информации принят от третьего источника, но не принят от первого и второго. На языке алгебры событий (или первый сценарий, или второй, или третий – т.е. сумма событий) это означает, что (обратите внимание, насколько эта запись короче словесного описания!), причем отдельные слагаемые несовместны. Поэтому  . .Поскольку пакеты информации поступают независимо то,  . Аналогично можно разложить в произведение две другие вероятности. Окончательно получаем: . Аналогично можно разложить в произведение две другие вероятности. Окончательно получаем: . .Учитывая, что  , ,  , ,  , имеем: , имеем: . .б) В обозначениях алгебры событий имеем: 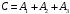 . В соответствии с рекомендацией перейдём к событию . В соответствии с рекомендацией перейдём к событию 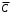 - не имело место ни одно из событий - не имело место ни одно из событий 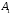 , ,  и и 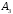 т.е. т.е.  , поэтому (используя независимость событий) , поэтому (используя независимость событий)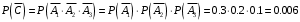 . .Тогда 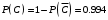 . .Задача 1.7. Два орудия стреляют в цель независимо друг от друга. Вероятность попадания для первого 0,8; для второго 0,7. Найти вероятность попадания в цель: а) двух орудий, б) только одного из двух, в) хотя бы Задача 1.6. Из букв разрезной азбуки составлено слово СТАТИСТИКА. одного. Какова вероятность того, что перемешав буквы и укладывая их в ряд по одной наудачу опять получим слово: СТАТИСТИКА |