КОНСПЕКТ ЛЕКЦИЙ Электротехника и электроника. Конспект лекций

• Название: Конспект лекций
• Анкор: КОНСПЕКТ ЛЕКЦИЙ Электротехника и электроника.docx
• Дата: 13.05.2018
• Размер: 252.3 Kb.
• Имя файла: КОНСПЕКТ ЛЕКЦИЙ Электротехника и электроника.docx
• Тип: Конспект; #19206
• страница: 3 из 4

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

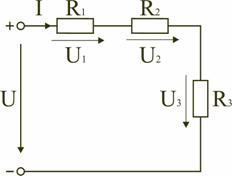
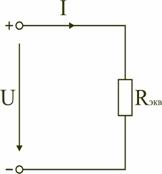
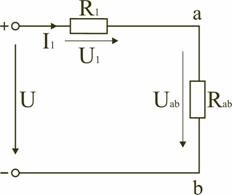
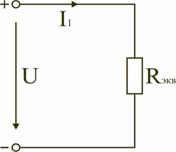
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ или IR_экв = IR₁ + IR₂ + IR₃,

откуда следует

R_экв = R₁ + R₂ + R₃.

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома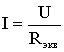

,

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).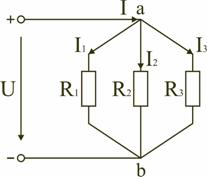



Рис. 1.6

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.е.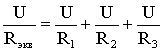



откуда следует, что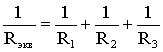

.

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

(1.7)

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g_экв = g₁ + g₂ + g₃.

По мере роста числа параллельно включенных потребителей проводимость цепи g_экв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR_экв = I₁R₁ = I₂R₂ = I₃R₃.

Отсюда следует, что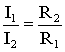

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.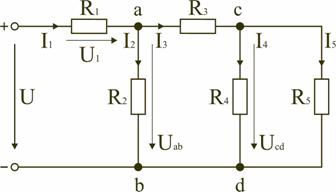



Рис. 1.7

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно: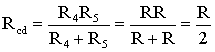

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):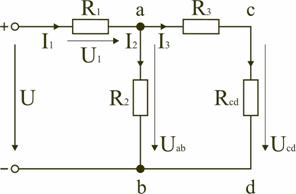



Рис. 1.8

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):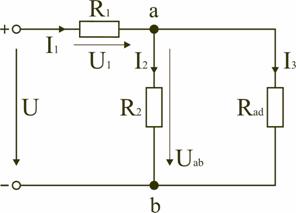



Рис. 1.9

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно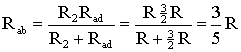

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).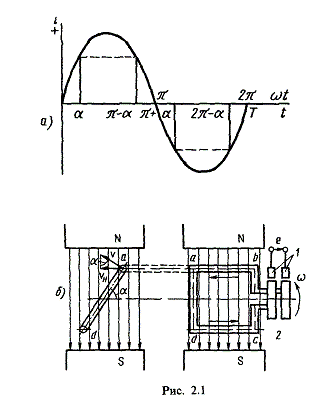



Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v_н:

e = Blv_н          (2.1)

где В и l - постоянные величины, a v_н - переменная, зависящая от угла α. Выразив скорость v_н через линейную скорость катушки v, получим

e = Blv·sinα          (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.

Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E_m = Blv. Поэтому выражение (2.2) можно записать в виде

e = E_msinα          (2.3)

Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде

e = E_msinωt          (2.4)

где е - мгновенное значение э. д. с. в катушке; α = ωt - фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.

Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе - время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е'.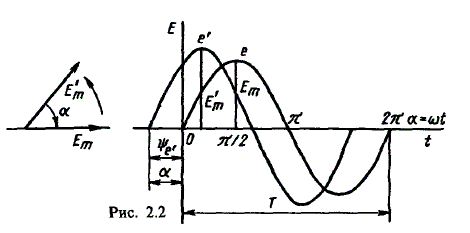



Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π, откуда

ω = 2π / T = 2πf          (2.5)

Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е' можно описать выражениями

e = E_msinωt; e' = E'_msin(ωt + ψ_e').

Здесь ωt и ωt + ψ_e' - фазы, характеризующие значения э. д. с. e и e' в заданный момент времени; ψ_e' - начальная фаза, определяющая значение э. д. с. е' при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ_e = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу - вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).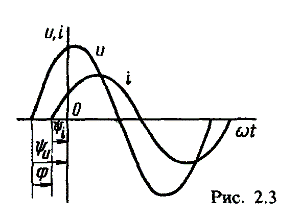



Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U_msin(ωt + ψ_u); i = I_msin(ωt + ψ_i),          (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ_u - ψ_i.

Уравнения (2.6) можно записать иначе:

u = U_msin(ωt + ψ_i + φ); i = I_msin(ωt + ψ_u - φ),

поскольку ψ_u = ψ_i + φ и ψ_i = ψ_u - φ.

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).

Формы представления синусоидальных электрических величин.

Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.

1). Аналитическая форма представления

I = I_m·sin(ω·t + ψ_i), u = U_m·sin(ω·t + ψ_u), e = E_m·sin(ω·t + ψ_e),

где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

I_m, U_m, E_m – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψ_i, ψ_u, ψ_e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.

Графики мгновенных значений тока и напряжения показаны на рис. 2.3

Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ_u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ_i < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током

φ = ψ_u – ψ_i = ψ_u – ( - ψ_i) = ψ_u + ψ_i.

Применение аналитической формы для расчёта цепей является громоздкой и неудобной.

На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением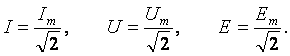


2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.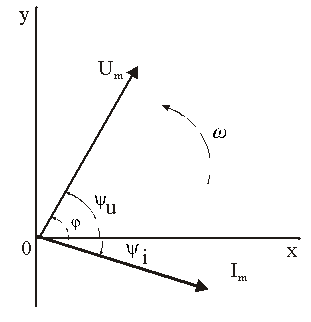


Рис. 2.4

Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4

3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.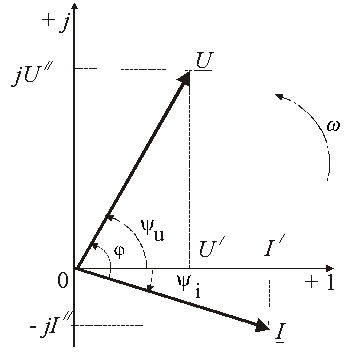


Рис. 2.5

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

а). Алгебраической

U = U’+ jU"

I = I’ – jI",

где U', U", I', I" – проекции векторов на оси действительных и мнимых чисел.

б). Показательной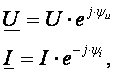



где U, I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

в). Тригонометрической

U = U·(cosψ_u + jsinψ_u)

I = I·(cosψ_i – jsinψ_i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е^j·ψ = cosψ + jsinψ.

Неразветвлённые электрические цепи

1). Цепь синусоидального тока с идеальным резистором.

Рассмотрим электрические процессы, возникающие в цепи, состоящей из идеального резистора.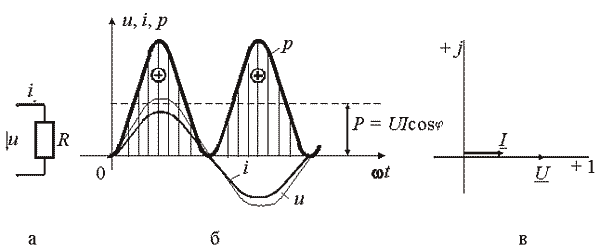



В резисторе происходит необратимый процесс преобразования электрической энергии в тепловую. Параметром, характеризующим это свойство резистора, является сопротивление R.

Пусть напряжение на резисторе изменяется по закону

u = U_m·sinω·t,

где начальная фаза для простоты принята равной нулю, ψ_u = 0.

Ток в цепи определяется по закону Ома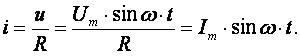



В этом выражении начальная фаза тока равна нулю (ψ_i = 0), т. е. На резисторе ток и напряжение совпадают по фазе, φ = 0. Амплитудные (как и действующие) значения связаны законом Ома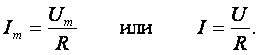



Мгновенная мощность, потребляемая резистором,

р = u·I = U_m·I_msin²ω·t = U_m·I_m·(1 – cos2·ω·t)/2 = U·I·(1 – cos2·ω·t).

Мгновенная мощность является положительной, рис.3.4, б. Это означает, что вся энергия, поступающая от источника, потребляется активной нагрузкой с сопротивлением R.

На практике пользуются средним значением мощности за период, которое называют активной мощностью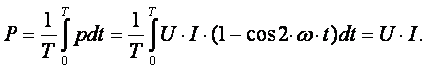



Активная мощность выражается в Вт. Учитывая, что

U = R·I, получаем P = R·I².

Запишем электрические величины в комплексной форме.

Напряжение и ток (действующие значения)



Комплексное сопротивление цепи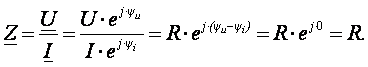



Активное сопротивление R является положительным действительным числом (мнимая часть комплексного сопротивления Z равна нулю).

2). Цепь синусоидального тока с идеальной индуктивностью.

Катушка индуктивности при протекании по ней тока обладает способностью создавать магнитное поле. Это свойство характеризуется параметром катушки, называемым индуктивностью L.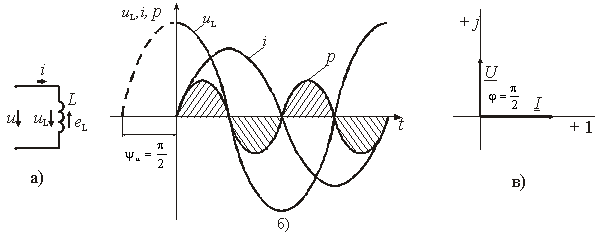


Для удобства анализа работы катушки в цепи переменного тока условно будем считать, что R_K = 0 (идеализированная катушка).

Пусть по катушке с числом витков w протекает ток, изменяющийся по закону I = I_m·sinω·t (начальная фаза принята равной нулю). Этот ток создаёт синусоидальный магнитный поток, мгновенное значение которого равно



где Ф_m – амплитуда потока 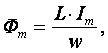а начальная фаза и частота равны начальной фазе и частоте тока.

Напряжение источника и = и_L уравновешивается ЭДС самоиндукции е_L катушки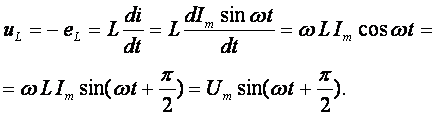



Из выражения видно, что начальная фаза напряжения ψ_u = π/2. Следовательно, синусоида напряжения на идеальной катушке индуктивности опережает синусоиду тока по фазе на угол π/2

φ = ψ_u – ψ_i = π/2 – 0 = π/2.

На практике, если напряжение по фазе опережает ток, говорят об индуктивном характере нагрузки. График мгновенных значений и векторная диаграмма тока и напряжения цепи с индуктивностью приведена на рисунке.

Амплитуда напряжения

U_m = ωLI_m,

откуда имеем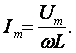



Действующее значение тока равно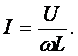



Это выражение представляет закон Ома для идеальной индуктивности.

Индуктивное сопротивление ωL выражается в омах и обозначается Х_L, т. е.

Х_L = ω L = 2 π f L.

Индуктивное сопротивление катушки имеет место только в том случае, когда происходит изменение тока во времени и зависит от скорости его изменения. При постоянном токе (f = 0) индуктивное сопротивление равно нулю.

Мгновенная мощность в индуктивном элементе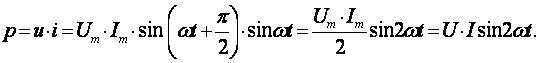



Амплитудное значение мгновенной мощности U·I называют реактивной мощностью

Q_L = U·I,

или учитывая, что U = X_L·I,

Q_L = X_L·I².

Реактивная мощность имеет размерность Baр.

Активная мощность в такой цепи, определяемая как средняя мощность за период, равна нулю, рис. б.

3). Цепь синусоидального тока с идеальным конденсатором.

Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость. Этот параметр является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u

q = C·u,

где q – выражается в кулонах [Кл], С – в фарадах [Ф], u – в вольтах [B].

При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток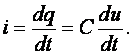



Идеализированный конденсатор обладает только параметром С.

Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом, рис., а.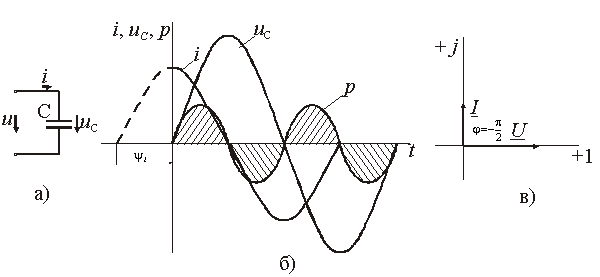



Пусть напряжение источника изменяется по закону

u = U_m·sinω·t, (ψ_u = 0).

В цепи возникает ток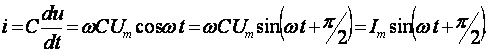



Из полученного выражения видно, что начальная фаза тока ψ_i = π/2. Угол сдвига фаз между напряжением и током составляет

φ = ψ_u – ψ_i = 0 – π/2 = - π/2.

Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол π/2, рис. 3.6, б, в. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.

Амплитуда тока

I_m = ω·C·U_m,

действующее значение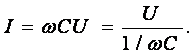



Это выражение представляет закон Ома. Величину 1/ω·C называют ёмкостным сопротивлением конденсатора и измеряют в [Ом]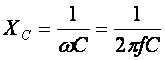

.

Ёмкостное сопротивление имеет место только в том случае, когда происходит изменение напряжения на обкладках конденсатора. При постоянном напряжении (f = 0) ёмкостное сопротивление равно бесконечности (т. е. В цепи будет разрыв).

Мгновенная мощность ёмкостного элемента



Амплитуда мгновенной мощности равна реактивной мощности

Q_C = U·I = X_C·I².

Активная мощность (средняя за период) равна нулю, рис., б.

С энергетической точки зрения график мгновенной мощности отражает накопление энергии в электрическом поле конденсатора (когда мощность положительная) и возврат её источнику питания (когда мощность отрицательная). Следовательно, ёмкостной элемент является реактивной нагрузкой.

Выразим электрические величины в комплексной форме. Напряжение и ток (действующие значения) в цепи имеют вид

U = U·e^j·ψu, I = I·e^j·ψi , ψ_u = 0, ψ_i = π/2, φ = - π/2.

Комплексное сопротивление цепи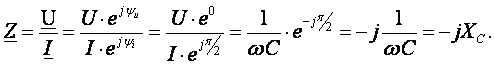



Ёмкостное сопротивление является отрицательным мнимым числом.
Последовательное соединение активного, индуктивного и ёмкостного элементов.

Рассмотрим процессы, происходящие в цепи, содержащей индуктивную катушку с параметрами L, R и конденсатор с параметром С. Схема замещения цепи показана на рисунке.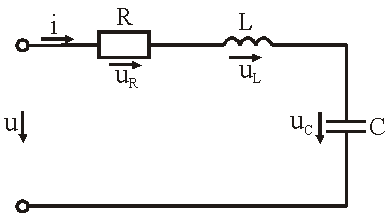



Для последовательной цепи общим является ток. Согласно второму закону Кирхгофа для мгновенных значений напряжение на входе цепи определяется выражением

u = u_R + u_L + u_C.

Запишем это уравнение в комплексной форме

U = U_R + U_L + U_C.

Представим это уравнение векторной диаграммой, рис. 3.8, а.

Построение векторной диаграммы начинаем с отложения на комплексной плоскости вектора тока I, который является общим для всех элементов цепи. Причём направление вектора выбираем произвольно. На рис 3.8, а вектор тока I выбран совпадающим с положительным направлением действительной оси. Вектор напряжения на активном сопротивлении U_R совпадает по направлению с вектором тока, его называют активной составляющей напряжения, U_R = R∙I. Вектор напряжения на индуктивности катушки U_L = jX_L∙I опережает вектор тока на угол 90°. Вектор напряжения на ёмкости U_C = - jX_C∙I отстаёт от вектора тока на угол 90°.

Геометрическая сумма трех векторов напряжения даёт вектор напряжения U, приложенного к цепи. Результирующий вектор напряжения U опережает вектор тока I на угол φ.

При построении диаграммы условно принято U_L > U_C. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником напряжений. Сторона треугольника

АВ = U_Х = U_L + U_C = j(X_L – X_C)·I

называется реактивной составляющей напряжения. Из треугольника напряжений можно найти модуль напряжения на зажимах в цепи



Заменяя напряжения на элементах произведением тока на соответствующие сопротивления, получаем

U = R·I + jX_L·I – jX_C · I = I·[R + j(X_L – X_C)] = Z·I,

где Z – полное комплексное сопротивление цепи,

Z = R + j(X_L – X_C).

Из треугольника сопротивлений можно определить модуль полного сопротивления и угол φ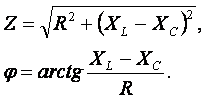



Мощность однофазной цепи синусоидального тока.

Активная мощность определяется выражением

P = U·I·cosφ = R·I² [Вт].

Она характеризует интенсивность необратимого преобразования электрической энергии в другие виды энергии.

Реактивная мощность определяется выражением

Q = U·I·sinφ = X·I² [Bap].

Она характеризует интенсивность колебательного обмена энергией между источником и реактивными элементами приемника без её преобразования.

Полная мощность определяется выражением

S = U·I = Z·I² [B·A].

Она характеризует амплитуду колебания мощности в цепи.


Комплексная мощность определяется выражением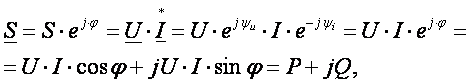



где - сопряженный вектор.

Умножив все стороны треугольника напряжений на ток, получаем треугольник мощностей, рис. 3.8, в.

Модуль полной мощности равен


ТРЕХФАЗНЫЕ ЦЕПИ.

Трехфазная система ЭДС.

Трехфазные электрические цепи представляют собой частный случай многофазных цепей.

Трехфазные цепи - это совокупность трех однофазных цепей, в которых действуют синусоидальные э. д. с. одной и той же частоты, сдвинутые по фазе друг относительно друга на угол 2π / 3. Передача электрической энергии на дальние расстояния по трехфазным цепям более выгодна, чем передача энергии по однофазным цепям; кроме того, трехфазные синхронные генераторы и двигатели, трехфазные асинхронные двигатели и трансформаторы более просты в производстве, экономичны и надежны в эксплуатации. В трехфазных системах достаточно просто получить вращающееся магнитное поле, воздействие которого на проводники с током положено в основу принципа работы асинхронных и синхронных электродвигателей.

Источником электрической энергии в трехфазной цепи является синхронный генератор, в трех обмотках которого, конструктивно сдвинутых друг относительно друга на угол 2π / 3 и называемых фазами, индуцируются три э. д. с., фазы которых, в свою очередь, также сдвинуты относительно друг друга на угол 2π / 3.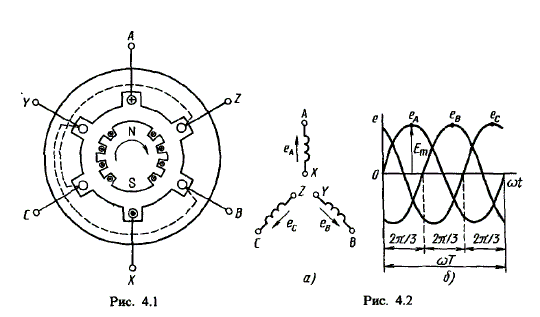



Мгновенные значения ЭДС трехфазного источника

e_A = E_m∙sinωt, e_B = E_m∙sin(ωt - 120°), e_C = E_m∙sin(ωt + 120°),

где начальные фазы соответственно равны

ψ_eA = 0;    ψ_eB = - 120°;   ψ_eC = 120°.

Такая система называется симметричной. Временная и векторная диаграммы показаны на рис. 4.2 а, б. Векторная диаграмма токов и напряжений строится на комплексной плоскости, оси которой +1, +j повернуты на 90° против направления часовой стрелки. Такое направление осей часто принимается при расчете трехфазных цепей (исключительно для удобства).