Движение материальной точки, теоретическая механика. Движение м.т 3 sc. Определение скорости и ускорения точки по заданным уравнениям ее движения
 Скачать 175.59 Kb.
|
|
Министерство науки и высшего образования Российской Федерации ФБГОУ ВО «Кубанский государственный технологический университет» (ФГБОУ ВО «КубГТУ») Институт машиностроения и автосервиса Кафедра наземного транспорта и механики ДОМАШНЯЯ РАБОТА по дисциплине: Теоретическая механика на тему: Определение скорости и ускорения точки по заданным уравнениям ее движения Выполнил студент гр. 19-ПБ-УК1 Божко Алина Юрьевна Проверил Хомутов Максим Павлович Краснодар 2020 Определение скорости и ускорения точки по заданным уравнениям ее движенияИсходные данные:  ;  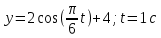.Найти: Траекторию движения точки, положение точки  при  , положение точки  в заданный момент времени t , скорость, ускорение и радиус кривизны точек  в заданный момент времени t .Решение  Рисунок 1 – расчетная схема для задачи Определяем траекторию движения точки  . .Возводим в квадрат и складываем левые и правые части  .Получим уравнение эллипса, которое имеет вид 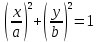 .Для данной точки, уравнение имеет вид  .центр эллипса в точке  ; ;горизонтальная полуось  м, вертикальная полуось  м.Определим положение точки при   . .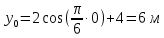Определим положение точки при   . .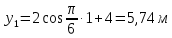Определим скорости и ускорения точек  . . . .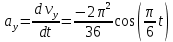Определим скорости и ускорения точки при  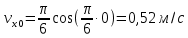. . . . . .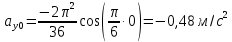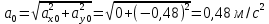Определим скорости и ускорения точки при  . .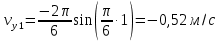 . . . .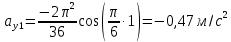Определим нормальное и тангенциальное ускорения по формулам радиус кривизны  ,где  ; .Определим нормальное и тангенциальное ускорения точки при  . .Определим нормальное и тангенциальное ускорения точки при  . .Определим радиус кривизны по формуле  .Определим радиус кривизны для точки при  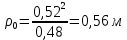.Определим радиус кривизны для точки при  .Ответ:  ;  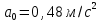;  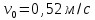;  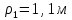;  ;  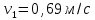.   |