Учебное пособие Физика. Адаптированный конспект по курсу физики. Конспект по курсу физики Для студентов специальности 1700201 Промышленное и гражданское строительство

• Название: Конспект по курсу физики Для студентов специальности 1700201 Промышленное и гражданское строительство
• Анкор: Учебное пособие Физика
• Дата: 27.02.2023
• Размер: 1.16 Mb.
• Имя файла: Адаптированный конспект по курсу физики.doc
• Тип: Конспект; #957295
• страница: 3 из 11

Интенсивность взаимодействия принято характеризовать с помощью безразмерной величины, пропорциональной вероятности процессов, обусловленных данным видом взаимодействия. Гравитационное взаимодействие является универсальным, ему подвержены все без исключения элементарные частицы, но оно обладает предельно малой интенсивностью. Понятие времени взаимодействия является весьма условным. Эмпирически его можно ввести как минимальное время жизни частиц, подверженных распадам за счет данного взаимодействия. Прочерк в соответствующей графе для гравитационного взаимодействия стоит потому, что предполагаемый переносчик гравитационного взаимодействия – гравитон - экспериментально пока не обнаружен.

2. Силы в механике. Наиболее фундаментальные силы, лежащие в основе всех механических явлений, это силы гравитационные и электрические. Сила тяжести относится к гравитационному взаимодействию, сила трения и силы упругости - к электромагнитному взаимодействию.

Сила тяжести F = mg , где m - масса тела, g - ускорение силы тяжести. Заметим, что вес тела P - это сила, с которой тело действует на опору или подвес P = m (g – a), где a - ускорение тела (и опоры) относительно Земли. Если а = g, то вес тела равен нулю Р = 0 (состояние невесомости).

Упругая сила – сила, пропорциональная смещению точки из положения равновесия и направленная к положению равновесия. Примером такой силы может быть сила упругой деформации при растяжении (сжатии) пружины или стержня. В соответствии с законом Гука эта сила определяется так:

F_упр. = - k∙∆l, где k - коэффициент жесткости пружины (стержня), ∆l - величина упругой деформации. Знак минус означает, что противоположны направления смещения точки и силы упругости, возникающей при этом смещении и действующей на смещенную точку.

Величина силы трения скольжения, возникающая при скольжении одного тела по поверхности другого, равна F_тр. = μN, где μ - коэффициент трения, зависящий от соприкасающихся поверхностей, N - сила реакции опоры.

Сила трения направлена в сторону противоположную направлению движения данного тела относительно другого.

Есть другие виды сил трения - силы трения покоя и сила трения качения.

Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости определяется зависимостью F_{сопр. =} αv, где v - скорость тела относительно среды, α - положительный коэффициент, характерный для данного тела и данной среды, при малых скоростях практически постоянен. Сила сопротивления всегда направлена противоположно вектору скорости тела.

Выталкивающая сила Архимеда равна весу вытесненной жидкости или газа: F_Арх. = gρ_срV, где ρ_ср. - плотность среды, V -объем тела, g - ускорение свободного падения.

2.2.3. Первый закон Ньютона.

Законы Ньютона представляют собой обобщение опытных данных (фактов). Эти законы устанавливались на основании наблюдений медленных по сравнению со скоростью света в вакууме движений.

1-й закон Ньютона.

Всякая материальная точка или тело сохраняет состояние покоя или равномерного прямолинейного движения, пока на них не действуют силы или действие сил скомпенсировано.

Этот закон называется законом инерции, а движение точки или тела, свободных от внешних воздействий, называется движением по инерции.

Покой - частный случай равномерного прямолинейного движения, когда

а = 0 и v = const, или v = 0.

Любое механическое движение - относительное движение, его характер зависит от системы отсчета. Закон инерции справедлив не во всех системах отсчета.

Системы, в которых выполняется первый закон Ньютона, называются инерциальными.

Системы, в которых не выполняется первый закон Ньютона, называются неинерциальными.

Инерциальных систем бесконечно много. Любая система, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, является также инерциальной системой.

2.2.4. Второй закон Ньютона.

Первый закон Ньютона говорит о состоянии тел, если на них не действуют силы. Каким будет движение, если на точку или тело действуют силы? Ответ на этот вопрос дает второй закон Ньютона, он связывает три величины - силу, массу и ускорение.

Второй закон Ньютона.

Произведение массы материальной точки (тела) на ее ускорение равно действующей на нее силе F = ma.

Если на тело действует несколько сил, то в формулировке 2-ого закона используется равнодействующая сила (см. Рисунок 7)

F_рез = ma.

Это является следствием независимости действия сил на тело (точку) или говорят, что силы подчиняются принципу суперпозиции. Такое утверждение надо рассматривать как обобщение опытных фактов.

Так как в классической механике а = dv/dt и m = const, то второй закон можно переписать в виде:



И еще один вид уравнения 2-ого закона:

F∙dt = dP

Величина F∙dt называется вектором импульса силы, а величина dP - вектор изменение импульса тела под действием данной силы.

Основное уравнение динамики (второй закон Ньютона в векторном виде) можно записать в проекциях на касательное направление и нормаль к траектории в данной точке, используя полученные ранее выражения для нормального и тангенциального ускорений (§2.1.4):

,

.

Если тело (или точка) вращается по окружности, то можно записать уравнение для силы, действующей по касательной к траектории 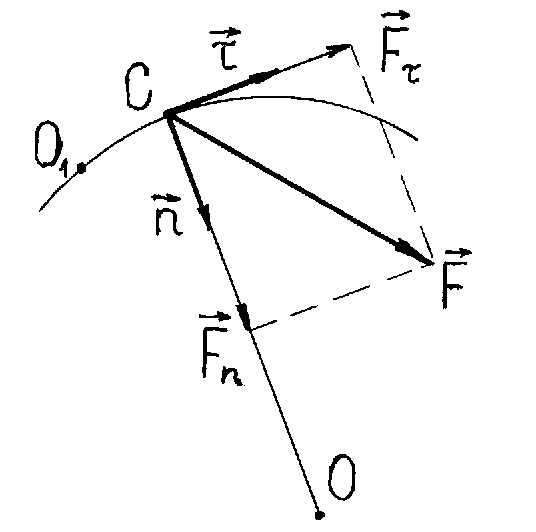, и для силы, действующей по радиусу окружности (Рисунок 8).


Рисунок 8 – Разложение вектора F на составляющие F_τ и F_n , R – радиус окружности, по которой вращается тело (или точка).

2.2.5. Третий закон Ньютона.

В первом и во втором законах Ньютона речь идет о силах, действующих на данное тело, и его движении под действием этих сил, но нет упоминания о других телах, со стороны которых эти силы действуют. Роль второго тела во взаимодействии отражена в третьем законе Ньютона.

3-й закон Ньютона.

Силы, с которыми два тела действуют друг на друга, равны по величине, направлены в противоположные стороны F₁₂ = - F₂₁.

F₁₂ - сила, действующая со стороны второго тела на первое, приложена к первому телу, F₂₁ - сила, действующая на второе тело со стороны первого, приложена ко второму телу (Рисунок 9).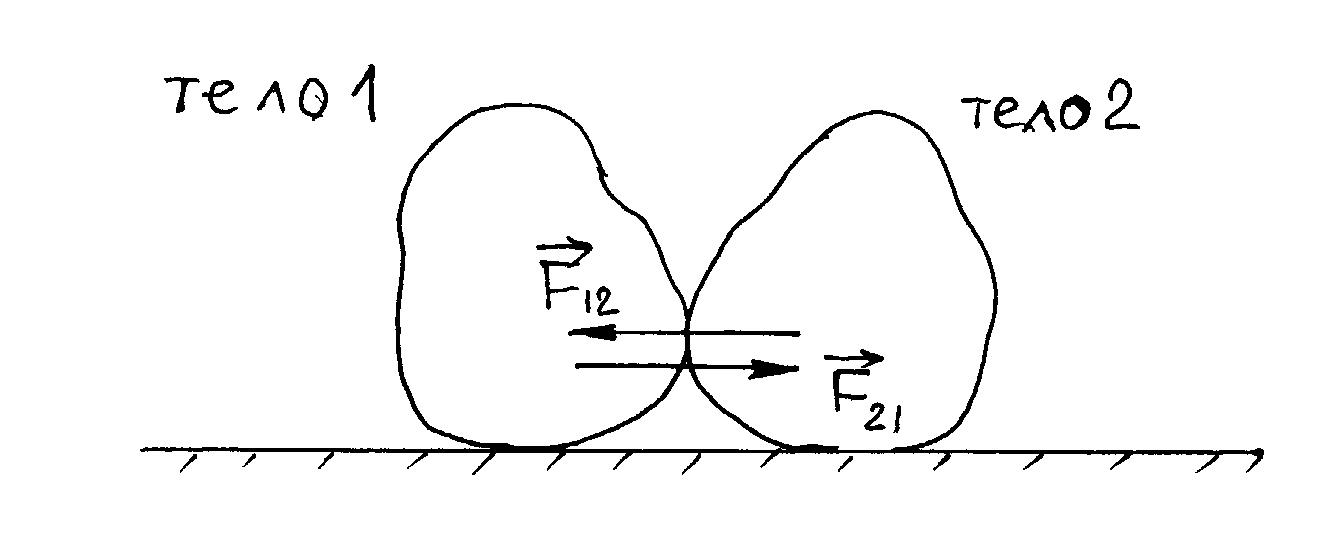

Рисунок 9- Взаимодействие двух тел.

2.2.6. Закон сохранения импульса.

1. Совокупность тел, частиц (например, в газе) или отдельное твердое можно рассматривать как систему материальных точек. Если система с течением времени изменяется, то это означает, что изменяется ее состояние. Зная законы действующих на частицы системы сил и состояние системы в начальный момент времени, можно с помощью уравнений движения рассчитать состояние системы в любой момент времени. Но в некоторых случаях это может быть задачей достаточно сложной (сложна сама система или неизвестны законы действующих сил, или детальное рассмотрение поведения отдельных частиц системы не имеет смысла, например, в газе).

Возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задач и обойти возникшие трудности? Оказалось, такие принципы есть. Это законы сохранения энергии, импульса и момента импульса (см. 7, стр. 52-57).

Эти законы справедливы не только в рамках классической механики. Все они являются универсальными законами природы, выполняются и в макромире, и в микромире, и во всей Вселенной. В настоящее время неизвестно ни одного эксперимента и ни одного физического явления, в котором упомянутые универсальные законы сохранения нарушались бы.

Закон сохранения импульса выполняется для замкнутых систем (см. §2.2.1 п.1).

2.Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из двух тел, применяя второй и третий законы Ньютона. Пусть первое тело, имеющее массу m₁, движется со скоростью , второе тело, масса которого m_2, движется со скоростью _2.

При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила ₁₂ =- _{21 ,} по второму закону Ньютона сила F_12, действующая на первое тело, изменит импульс первого тела, можно записать ₁₂= , точно так же можно записать, что сила F₂₁ изменит импульс второго тела: ₂₁= . Подставим значения F₁₂ и F₂₁ в третий закон Ньютона: =- , т.к. время взаимодействия - одно и то же, то: =- или + = .

Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы = + ,

+ = - это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса =0, следовательно, полный вектор импульса системы при взаимодействии не изменился: если =0, то P = const.

Если система состоит из N тел, то P = m₁∙v₁ + m₂∙v₂ + ........+ m_N∙v_N есть полный вектор импульса замкнутой системы, и P = const.

Закон сохранения импульса (ЗСИ).

Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы. Только внешние силы изменяют импульс системы.

3. Если векторная сумма внешних сил не равна нулю, то надо посмотреть, нет ли такого направления, вдоль которого внешние силы не действуют или сумма их проекций на это направление равна нулю. Если такое направление в движении тел, входящих в систему, есть, то можно применять закон сохранения для проекции полного вектора импульса системы на выделенное направление.

2.2.7. Динамические характеристики вращательного движения. Момент силы. Момент импульса.

При поступательном движении системы все ее точки проходят одинаковые пути, имеют в данный момент времени одинаковые скорости и ускорения. При вращательном движения твердого тела все эти характеристики различны для разных точек вращающегося тела, поэтому и математическая форма 2-го закона Ньютона будет иной. При вращательном движении существенно изменяются сами понятия причины, вызывающей вращение, и величины, определяющей инертность тела.

При поступательном движении динамическими характеристиками являются сила, масса, импульс. При вращательном движении динамическими характеристиками являются момент силы, момент инерции, момент импульса. Эти характеристики можно рассматривать относительно точки вращения (полюса) и относительно оси вращения. В дальнейшем будем рассматривать эти характеристики относительно оси вращения. Определим эти характеристики.

1.Момент силы, действующей на материальную точку, относительно оси вращения.

а) Пусть материальная точка массы m вращается относительно оси ОО΄. Обозначим r - радиус-вектор, проведенный от оси вращения до точки приложения силы F (Рисунок 10).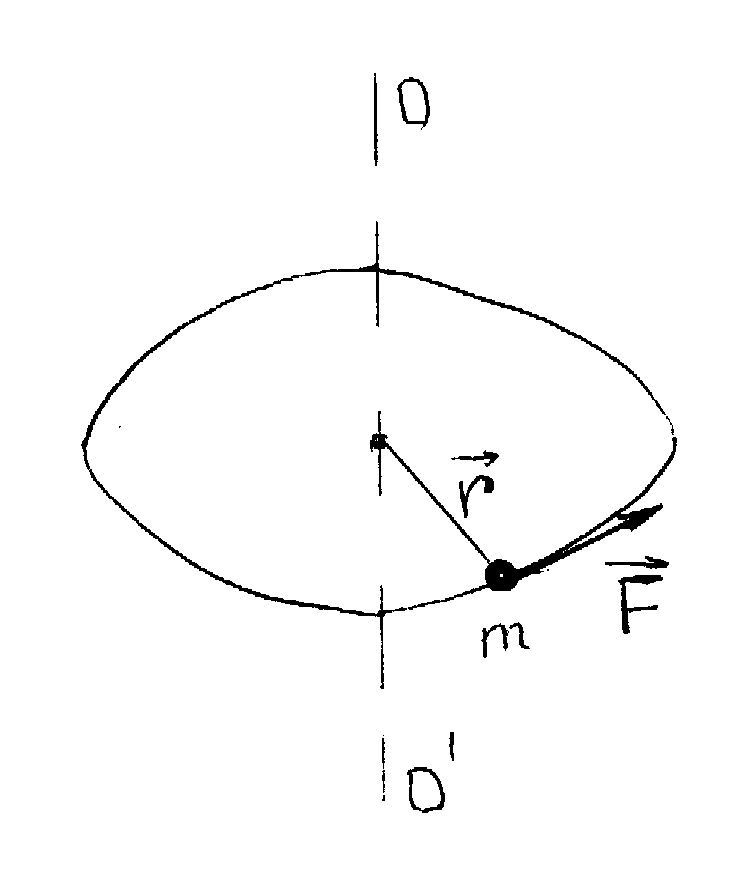



Рисунок 10. Вращение материальной точки
Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [r∙F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика

Модуль вектора момента силы равен M = F∙r∙sinα, где α - угол между векторами r и F.

2. Момент импульса.

Моментом импульса материальной точки относительно точки называется вектор L, равный векторному произведению радиуса-вектора r на вектор импульса P: L = [r∙P] = [r∙mv],

где m, v - соответственно масса и вектор скорости точки. Направление L определяется по правилу правого буравчика. Модуль вектора L = mv∙r∙sinα, где α - угол между векторами r и v.

Проекцией момента импульса материальной точки относительно оси вращения называется величина L, равная произведению импульса Р на радиус окружности R_z, по которой движется точка относительно некоторой оси вращения Z.

L_z = mv∙R_z

3. Момент инерции материальной точки относительно оси вращения

Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения (Рисунок 10).
I = m∙r²
Момент инерции - величина скалярная.

Единица измерения момента инерции является 1 кг∙м²

Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения.

I = m_i∙r_i²

Для твердого тела, разбитого на элементарные массы ∆ m_i , момент инерции относительно оси равен I = ∆ m_i∙r_i².

Моменты инерции тел правильной геометрической формы могут быть легко вычислены. Вычисления проводятся методом интегрирования бесконечно малых элементов инерции, выбираемых исходя из геометрической симметрии тел правильной формы. В Таблице 2 приведены результаты расчетов моментов инерции для тел правильной формы относительно оси вращения ОО', проходящей через их центр масс.


Для расчета моментов инерции вращающихся тел вокруг оси, не проходящей через центр масс тела, можно использовать теорему Гюйгенса-Штейнера. Применение этой теоремы позволяет экспериментально определить момент инерции тела произвольной формы по известному периоду колебаний тела правильной формы заданной массы, что весьма полезно на практике.

4.Теорема Штейнера.

Момент инерции тела относительно произвольной оси АА' равен сумме момента инерции тела относительно оси ОО', проходящей через центр масс тела и параллельной данной оси АА', и произведения массы тела как целого на квадрат расстояния d между осями АА' и ОО' (Рисунок 11).

I_АА' = I_ОО' + md²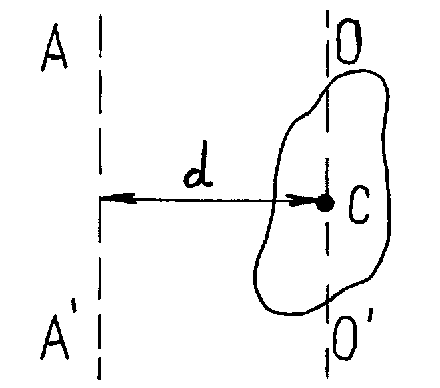

Рисунок 11.
Пример. Применение теоремы Штейнера для расчета момента инерции стержня длины l и массы m (см. Таблицу 2), если ось вращения проходит не через центр масс, а через конец стержня, приводит к следующему:

I_АА' = I_ОО' + md² = .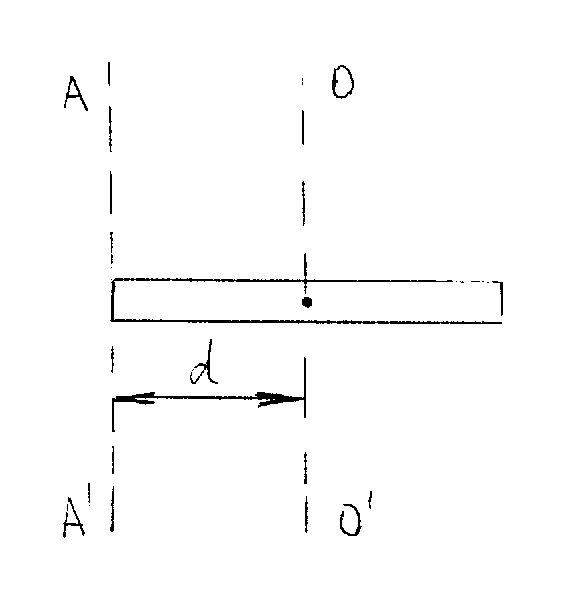

Рисунок 12. Вращение стержня вокруг оси

2.2.8. Основное уравнение динамики вращательного движения.

1. В разделе "Кинематика" при рассмотрении поступательного и вращательного движений мы показали, что кинематические уравнения обоих движений имеют одинаковый вид, но при поступательном движении мы используем линейные характеристики (путь, скорость, ускорение), а при вращательном - угловые характеристики (угловое перемещение, угловую скорость, угловое ускорение). Используем эту аналогию и в динамике. При поступательном движении уравнение второго закона Ньютона имеет вид dP/dt = F.

Для вращательного движения: dL/dt = M.

Это уравнение называется уравнением моментов или основным законом вращательного движения. Вид уравнения не изменится и для системы материальных точек и для вращения твердого тела, только L определяется как момент импульса для системы точек.

2. Еще один вид уравнения второго закона Ньютона для вращательного движения имеет вид:

M∙dt = dL,

где величина M∙dt называется импульс момента сил, а dL - изменение момента импульса системы.

2.2.9. Закон сохранения момента импульса.

Обратимся к уравнению моментов dL/dt = M, где M - главный вектор момента внешних сил.

Если M = 0, то и L = const.

Если относительно некоторой точки О выбранной системы отсчета момент всех сил, действующих на систему материальных точек, равен нулю, то относительно этой точки вектор момента импульса системы не изменяется с течением времени (закон сохранения момента импульса относительно полюса).

Примеры.

а) Человек стоит на скамье Жуковского, представляющей массивный, диск, который может вращаться вокруг оси, проходящей через его центр, с пренебрежимо малым трением. Момент импульса системы "человек - диск" равен нулю. Человек начинает идти вдоль обода диска. Диск начинает вращаться в обратную ходу человека сторону.

б) Фигурист выполняет "волчок", его руки раскинуты в стороны, его момент инерции относительно вертикальной оси вращения I₁, угловая скорость ω₁. Затем он резко прижимает руки к груди, его момент инерции уменьшается и становится I₂, а угловая скорость ω₂ увеличивается. При этом выполняется закон сохранения момента импульса относительно вертикальной неподвижной оси, проходящей через линию симметрии тела фигуриста I₁∙ω₁ = I₂∙ω₂.