Учебное пособие Физика. Адаптированный конспект по курсу физики. Конспект по курсу физики Для студентов специальности 1700201 Промышленное и гражданское строительство

• Название: Конспект по курсу физики Для студентов специальности 1700201 Промышленное и гражданское строительство
• Анкор: Учебное пособие Физика
• Дата: 27.02.2023
• Размер: 1.16 Mb.
• Имя файла: Адаптированный конспект по курсу физики.doc
• Тип: Конспект; #957295
• страница: 4 из 11

2. 3. Работа и механическая энергия.

2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы.

В физике работа неразрывно связана с изменением состояния тела или системы. Это изменение может выражаться самым различным образом: а) тело приобретает другую скорость, б) тело поднимается на другой уровень, в) тело деформируется, г) тело заряжается, д) тела намагничивается и т.д. Состояние механической системы (или тела) характеризуется одновременным заданием координат и скоростей всех точек системы (или тела) и может изменяться в процессе движения.

Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса вводят понятия силы и работы, совершаемой силой.

1.Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r:

∆А = (F∙∆r) = F∆rcos  ,

где  - угол между направлениями векторов силы F и перемещения ∆r, (F∙∆r) – скалярное произведение двух векторов (см.[8]).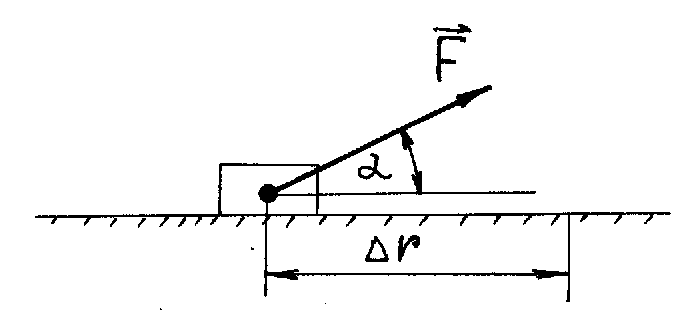

Рисунок 13 - Перемещение тела под действием постоянной силы.

Работа ∆А - скаляр. Если угол  - острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол  - тупой, то ∆А - отрицательная величина, и говорят, что работа совершается против действия силы. Если  = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.

На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F_i и ∆r_i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F_i на своем малом участке (Рисунок 14):

А = ∆А₁ + ∆А₂ +....+ ∆А_N = (F₁∙∆r₁) + (F ₂∙∆r₂) + ...+(F _N∙∆r_N) = (F_i∙∆r_i),

где i = 1,2......N - номер элементарного участка траектории.


Рисунок 14 - График зависимости силы от пути.

На участке ∆r_i силу F_i можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆r_i равна ∆А_i=F_i∙∆r_i и равна площади заштрихованной фигуры на рисунке 14.

А= ∆ А_i - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

3.Примеры вычисления работы.

а) Тело, поднятое над землей на высоту h, падает на землю (без трения) из точки В в точку С и возвращается обратно (Рисунок 15). Определить работу силы по замкнутому пути.

Сила, действующая на тело, постоянна и равна силе притяжения тела к Земле (сила тяжести). Работа этой силы на участке ВС равна .

Чтобы поднять тело без ускорения из точки С в точку В, надо приложить к телу силу, равную силе тяжести, но противоположно направленную, и работа на участке пути СВ равна (работа совершается против силы тяжести).

Полная работа на участке (ВС+СВ) равна нулю.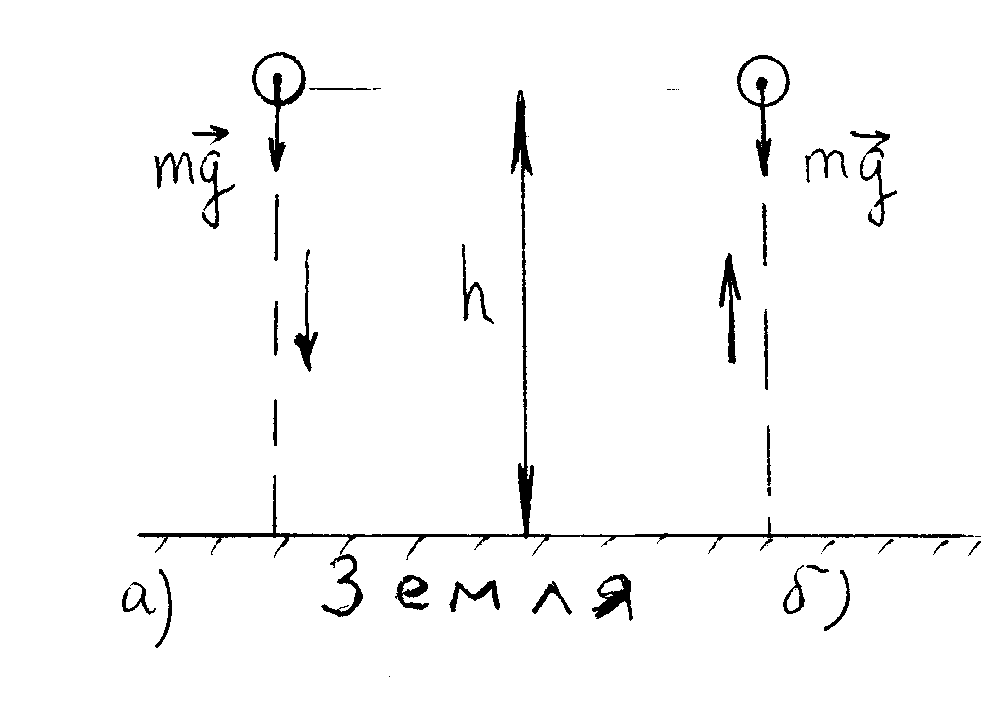


Рисунок 15. Падение тела с высоты h (a) и поднятие тела на высоту h (б)

б) Пружину длиной l₁ растягиваем до длины l₂. Какая работа при этом совершается?

Пусть х - длина, на которую растянута пружина, отсчет х от положения равновесия (Рисунок 16). При этом на пружину будет действовать упругая сила, старающаяся вернуть пружину в состояние равновесия, что соответствует минусу в формуле F = - kх (закон Гука). Если растянуть пружину еще на малую длину ∆х, надо совершить элементарную работу ∆А = - kх∙∆х.

Возникающая упругая сила будет переменной, т.к. она зависит от длины, на которую растягивают пружину. Для определения работы, которую надо затратить для растяжения пружины от длины l₁ до l₂, надо воспользоваться операцией интегрирования: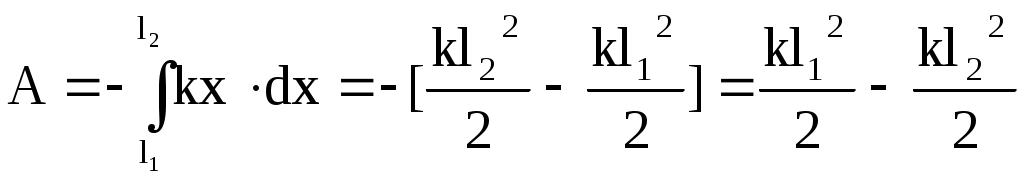



Работа силы упругости определяется только начальным и конечным положением пружины.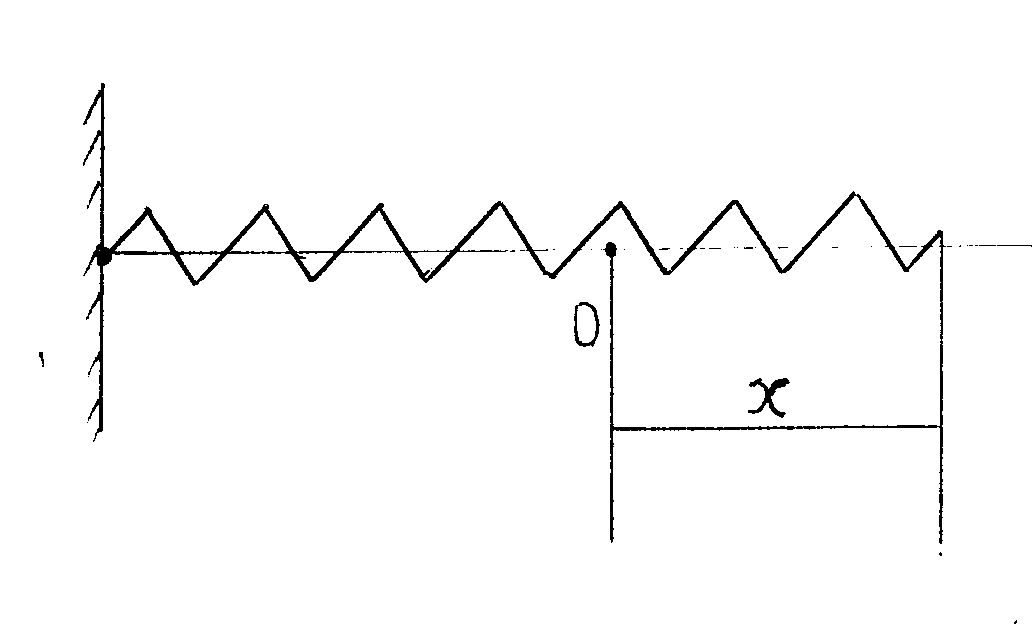


Рисунок 16. Сжатие пружины
4. Полная работа внешних сил при вращательном движении тела равна произведению момента этих сил относительно оси вращения на угол поворота тела за время действия сил. ∆A=М∆ .

И момент сил, и угловое перемещение (равное по модулю углу поворота) - векторы, направленные вдоль оси вращения. Если направление этих векторов совпадает, то ∆A>0. Если направление этих векторов противоположное, то ∆A<0.

5. Силы, работа которых определяется только начальной и конечной точками их приложений, и не зависят ни от вида траектории, ни от характера движения тела, называются консервативными или потенциальными силами.

Другое определение для этих сил таково. Силы, работа которых по замкнутой траектории равна нулю, называются потенциальными.

Соответственно, если работа силы по замкнутой траектории не равна нулю, то такая сила неконсервативная (непотенциальная).

К непотенциальным силам относятся силы трения и силы, величина которых зависит от скорости движения точки (тела).

Сила тяжести и сила упругости являются потенциальными силами (см. приведенные выше примеры).

2.3.2. Энергия.

1. Наиболее общим определением понятия энергии можно считать то, которое связано с понятием состояния системы (или тела). Энергия всегда является функцией состояния системы (тела). В любом состоянии система имеет определенное значение энергии и может сохранять это состояние, а значит и энергию этого состояния, сколь угодно долго. Для перехода системы (тела) в другое состояние должна быть совершена работа.

Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией.

Состояние системы (тела) может меняться в процессе движений. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии. Поэтому можно дать другое определение для энергии.

Энергией называется физическая величина, являющаяся общей мерой различных форм движения материи.

Различают виды энергии механическую, внутреннюю, электромагнитную, химическую, ядерную и т.д.

Механическая энергия может быть обусловлена или движением тела с некоторой скоростью (кинетическая энергия), или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия) W_мех. = W_кин. + W_пот..

2.3.3. Кинетическая энергия.

1. Кинетической энергией тела называется энергия его механического движения.

Изменение кинетической энергии тела под действием силы равно работе этой силы.

Физическая величина называется кинетической энергией, а величина , равная разности кинетических энергий конечного состояния системы (индекс 2) и начального состояния (индекс 1), называется приращанием кинетической энергии.

Если на тело действуют несколько сил, и каждая из них совершает работу, и в результате этого меняется кинетическая энергия тела, то полная работа равна алгебраической сумме работ всех сил, действующих на тело. Энергия тела меняется за счет совершения работы.

Итак, связь работы и кинетической энергии задается соотношением:

А_{всех сил} = ∆W_кин = (W_кин)_кон. - (W_кин.)_нач.,

т.е. работа всех сил равна изменению кинетической энергии тела (или системы).

Работа - мера изменения энергии (физический смысл работы).

2. Кинетическая энергия вращающегося тела.

Твердое тело вращается вокруг неподвижной оси. Полная кинетическая энергия вращающегося тела равна:

,

где I - момент инерции тела относительно оси вращения. Посмотрим, как получается данная формула.
Рассмотpим кинетическую энеpгию вpащающегося вокpуг неподвижной оси т 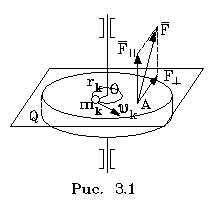веpдого тела. Она pавна сумме кинетических энеpгий отдельных частиц тела, движущихся с различными скоpостями

                                                                                                                           
Однако все точки тела имееют одну и ту же угловую скоpость. Поэтому целесообpазно пеpейти от линейных скоpостей частиц тела к угловой скоpости тела. Все точки движутся по окpужностям (pис.3.1) а, значит V_k=r_k*ω. Подставляя эту фоpмулу, получаем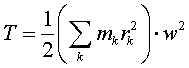



                                                                                                                           
        Сумма, стоящая пеpед квадpатом угловой скоpости, для абсолютно твеpдого тела пpедставляет собой некотоpую постоянную величину, зависящую лишь от pаспpеделения масс частей тела. Эта величина обозначается чеpез J и называется моментом инеpции тела относительно оси (в нашем случае относительно оси вpащения). Таким обpазом, кинетическая энеpгия тела с неподвижной осью вpащения имеет вид