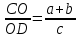Главная страница
Навигация по странице:

  • Актуализация нового материала.

  • Проверка домашнего задания.

  • Объяснение нового материала.

  • Закрепление учебного материала. Задача 1.

    		•

    8 геометрия. 8 геом. Конспект урока по геометрии 8 класс Тема урока Свойства биссектрисы треугольника. Ход урока Организационный момент


    Скачать 149.2 Kb.
    НазваниеКонспект урока по геометрии 8 класс Тема урока Свойства биссектрисы треугольника. Ход урока Организационный момент
    Анкор8 геометрия
    Дата08.04.2022
    Размер149.2 Kb.
    Формат файлаdocx
    Имя файла8 геом.docx
    ТипКонспект
    #453978


    Конспект урока по геометрии 8 класс
    Тема урока: Свойства биссектрисы треугольника.
    Ход урока

    1. Организационный момент.

    Взаимное приветствие учителя и учащихся.

    1. Актуализация нового материала.

    • Устная фронтальная работа по обобщению теоретического материала.

    Какие из следующих утверждений верны?

      • Биссектриса всегда проходит через середину стороны треугольника.

      • Любая биссектриса равнобедренного треугольника является его медианой.

      • Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

      • Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

      • Биссектриса всегда проходит через середину стороны треугольника.

      • Любая биссектриса равнобедренного треугольника является его медианой.

      • Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

      • Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

    • Определение темы урока и постановка целей урока совместно с учащимися.

    1. Проверка домашнего задания.

    Защита мини-проектов (каждому по 2-3 мин) по схеме (свойство биссектрисы, доказательство ‒ только в презентации, задача для устного счета, сложная задача на применение свойства (желательно из ОГЭ или ЕГЭ), практическое использование данного свойства в современной жизни).
    Факт
    Рисунок
    Докладчик
    Задача



    Каждая точка биссектрисы угла находится на одинаковом расстоянии от сторон этого угла



    Артем Лазарев
    №676 (а)



    Биссектриса треугольника делит третью сторону на отрезки, пропорциональные двум другим сторонам.



    Катя Артюшенко

    Вова Бублик Лакейчук Ульяна

    Казаковцева Катя

    Жмаев Захар

    Чижма Юля

    1. В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC, если АС = 4; DC = 2; BD = 3.

    2. В треугольнике MNK известны длины сторон MN=4см, NK=5см, NP — биссектриса, а разность длин отрезков MPи PK равна 0,5см. Найдите MP и PK.

    3. В прямоугольном треугольнике АВС с прямым углом С биссектриса ВК делит катет АС на отрезки АК = 15 и КС = 12. Найдите площадь треугольника АВК.



    Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный, а третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит



    Саша Рекунова
    Дано:

    АВС - равнобедренный треугольник

    ВН=8см

    АС : АВ = 6 : 5

    Найти: ВО.



    Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

    Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника



    Дмитриева Даша

    Байдина Арина

    Полянская Ангелина
    Докажите, что биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.



    Угол, образованный при пересечении двух биссектрис треугольника, равен половине третьего угла + 90º.


    Литвинов Павел

    Рамзаев Семён

    Лапушкин Денис

    1. Биссектриса угла D и биссектриса угла C треугольника DEC пересекаются в точке M. 
      Найдите ∠EMC, если ∠EDC = 40°.

    2. В треугольнике ABC угол C равен 580, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.



    Точка пересечения биссектрис делит биссектрису угла C в отношении .




    Конюхова Олеся

    1. Дано:

    ABC - треугольник, со сторонами a, b, c.

    c = 6, a = 4, DO = 7, CO = 6.

    Найти:

    Сторону b.

    1. Дано:

    ABC- треугольник и стороны a, b, c.

    DO= 9, a= 8, b= 4, c= 3.

    Найти:

    биссектрису СО.




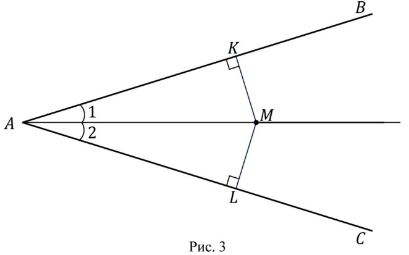
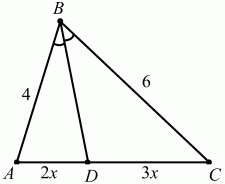
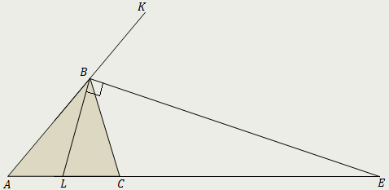
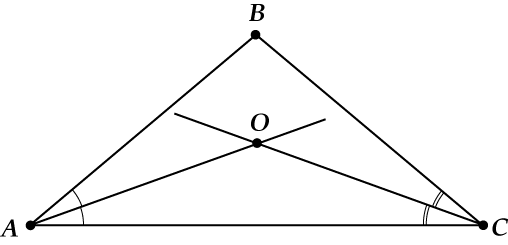
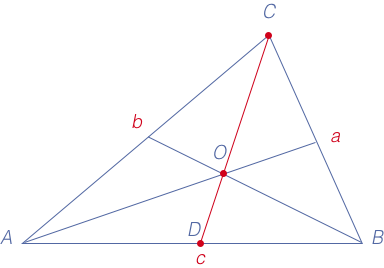
    1. Объяснение нового материала.

    • Биссектрисы треугольника пересекаются в одной точке.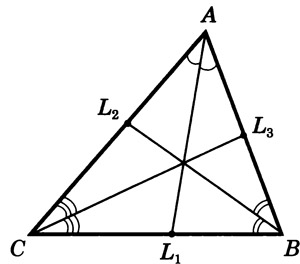



    • Биссектриса угла параллелограмма отсекает равнобедренный треугольник.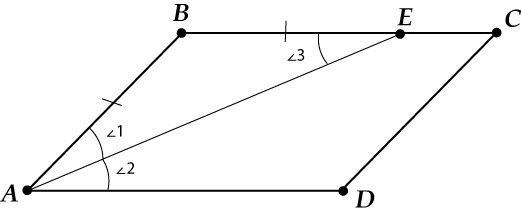



    • Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.



    • Теорема Менелая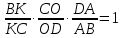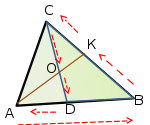

    .





    1. Закрепление учебного материала.

    Задача 1. Точка пересечения биссектрис делит биссектрису угла C в отношении .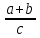

    Задача 2. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите: а) в каком отношении точка О делит биссектрису С; б) отношение площади треугольника ABK к площади четырёхугольника KPCM.

    1. Итог урока

    Запись домашнего задания.

    • Выучить 5 любых свойств

    • Решить 2 задачи на выбор

    Рефлексия урока.

    написать администратору сайта