Расчет электропривода. Расчет электропривода Смирнов Д.В. Конструкторская часть Выбор электродвигателя
 Скачать 2.14 Mb.
|
|
Таблица 1.3
ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ При рассмотрении функциональной схемы электропривода в предыдущем разделе, было отмечено, что схема содержит два канала регулирования: потокосцепления с внутренним контуром составляющей тока статора i1x и скорости с внутренним контуром составляющей тока статора i1y. Задание на потокосцепление соответствует номинальному и также было рассчитано ранее. Задание на скорость поступает через задатчик интенсивности, согласно рассчитанной тахограмме. В представленной схеме, также, необходимо особое внимание уделить косвенной ориентации. Как было сказано выше, полная управляемость электропривода обеспечивается, если обеспечивается управление электромагнитным моментом двигателя. А он в первую очередь зависит от потока. Необходимо четко обеспечить косвенную ориентацию вектора потокосцепления ротора по оси x. Запишем уравнение ротора в установившемся режиме: 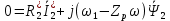 Абсолютное скольжение: 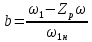 Потокосцепление ротора определяется: 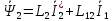 Отсюда получаем: 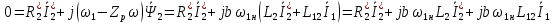 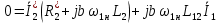 Выражаем ток ротора: 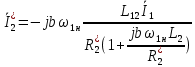 Подставляем ток рота в формулу потокосцепления: 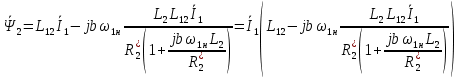 Приводим формулу к общему знаменателю: 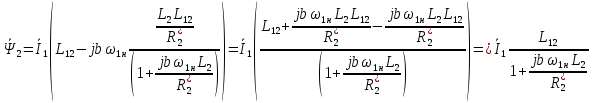 Представим ток статора в виде проекции на оси x и y: 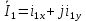 Отсюда потокосцепление: 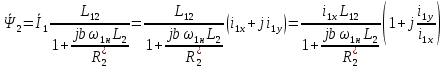 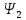 представляет собой вещественную часть, ориентированную по оси х. Определяем его по проекциям на эту ось: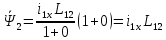 Найдем проекцию на ось y: 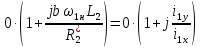 Отсюда получаем соотношение: 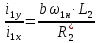 Это выражение является косвенной ориентацией. Таким образом, нужно обеспечить его выполнение с помощью системы регулирования. В моделе Matlab, изображенной на рис.2.1 и являющейся частью общей модели электропривода, условие косвенной ориентации используется при вычислении задание на угловую частоту вращения поля статора. 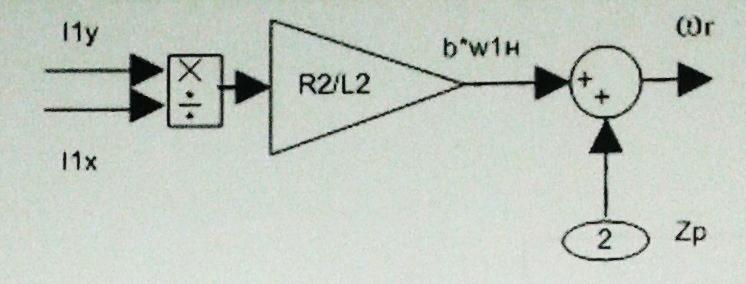 Рис. 2.1. 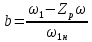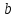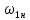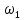Условие косвенной ориентации в модели Matlab Абсолютное скольжение вычисляется: где  – абсолютное скольжение;ω – угловая скорость вращения ротора;  – номинальная частота вращение поля статора; – заданная частота вращения поля статора.Отсюда заданную частоту определяем как: 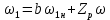 Из условия косвенной ориентации определяем: 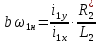 Таким образом, изменение скорости поля осуществляется в соответствие с условием косвенной ориентации. Потокосцепление при любых режимах оказывается ориентированным по оси х. Определив все параметры выбранной системы, учитывая произведенные ранее расчеты, построенные тахограмму и нагрузочную диаграмму, составим математическую модель электропривода в программе Matlab Simulink (рис. 2.2, 2.3). 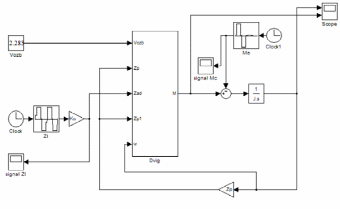 Рис. 2.2. Модель электропривода Для наглядности раскроем субсистему представленной модели (рис. 2.3). 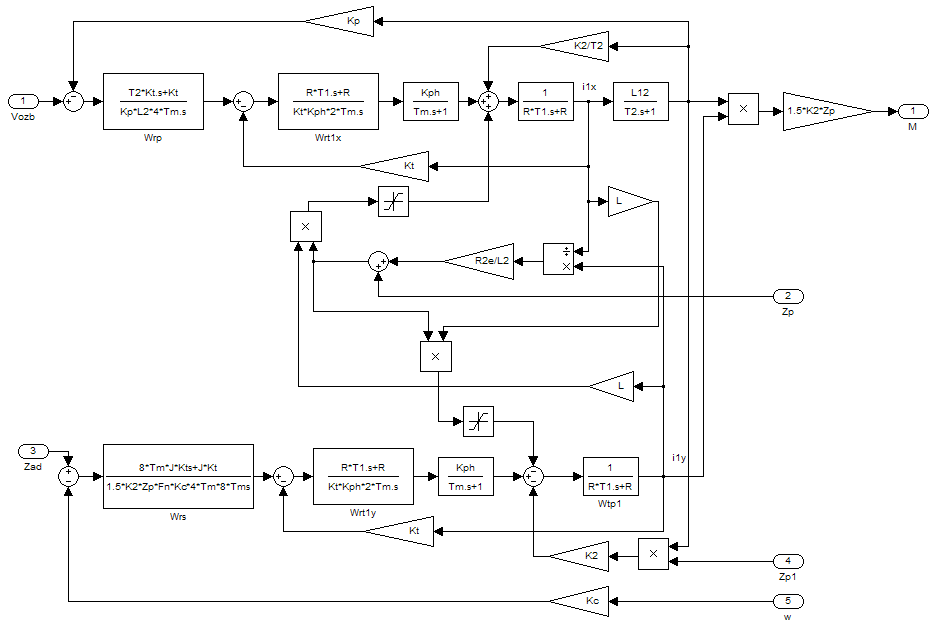 Рис. 2.3. Субсистема модели электропривода На вход системы подаем сигнал задания скорости, соответствующей рассчитанной ранее тахограмме работе электропривода. Сигнал задания по скорости, показан на рисунке 2.4. Сигнал задания по потокосцеплению задаем постоянной величиной, полученной в ходе расчетов в предыдущем разделе. 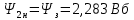 . 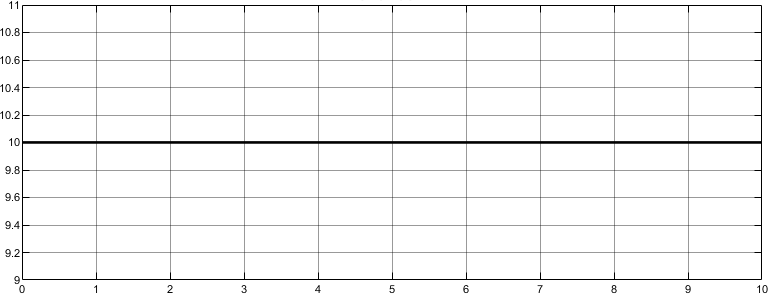Рис. 2.4. Сигнал задания В схеме, также, предусмотрен прибор, фиксирующий сигнал возмущения, которым является диаграмма статического момента Мс (рис. 2.5). 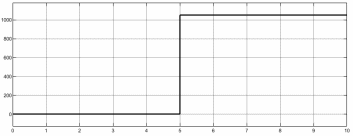 Рис. 2.5. Сигнал возмущения Модель работает следующим образом. Сначала подается сигнал задания по потокосцеплению, затем, спустя 1-2 секунды, от задатчика интенсивности подается задание по скорости. В конечном итоге, с учетом подаваемого сигнала возмущения, на выходе модели по приборам необходимо зарегистрировать изменения графиков момента и скорости. Произведя моделирование по своим параметрам, получим следующие результаты. На рис. 2.6. показано изменение момента и скорости за один цикл работы электропривода. 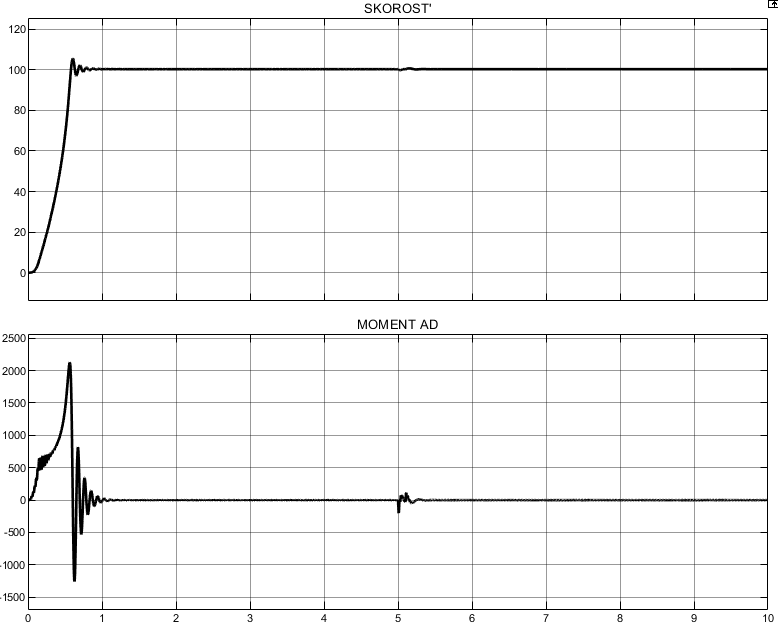 Рис. 2.6. Графики скорости и момента Полученные при моделировании графики подтвердили сделанные ранее теоретические выводы. С учетом помех они вполне соответствуют ожидаемым результатам и требуемым параметрам. Таким образом, проведя моделирование системы, мы доказали работоспособность выбранного электропривода с учетом всех параметров, определенных в ходе выполнения данной работы. |
