Расчет электропривода. Расчет электропривода Смирнов Д.В. Конструкторская часть Выбор электродвигателя
 Скачать 2.14 Mb. Скачать 2.14 Mb.
|
|
Функциональная схема электропривода В первую очередь, необходимо осуществить выбор принципа регулирования. Для этого рассмотрим возможные варианты регулирования. Учитывая небольшой диапазон регулирования, возможен вариант обычного U/f регулирования. Но данная система регулирования разомкнутая. В статическом режиме разомкнутая система частотного управления с соотношениями U/f практически обеспечивает сохранение номинальной перегрузочной способности АД в диапазоне изменения частоты не более 10:1 при постоянной нагрузке. При сохранении же заданной точности регулирования скорости АД диапазон ее регулирования в разомкнутой системе частотного управления значительно меньше, при постоянной нагрузке и точности регулирования 10% он не превышает диапазона 3:1. Недостатком разомкнутой системы частотного управления является и отсутствие переменных электропривода (моментов, токов, напряжений) при возможных перегрузках со стороны рабочего механизма или отклонениях напряжения питающей сети, что недопустимо. Формирование требуемых статических и динамических свойств асинхронного частотно-регулируемого электропривода возможно лишь в замкнутой системе регулирования его координат. Рассмотрим варианты скалярного и векторного управления. Скалярный принцип частотного управления является наиболее распространенным в электроприводе. Ему свойственна техническая простота измерения и регулирования абсолютных значений переменных АД, их стабилизация и ограничение в допустимых пределах внутренних переменных АД (токов статора и ротора, их потокосцеплений, основного магнитного потока), из-за сложных функциональных зависимостей между ними весьма ограничена. И если в статических режимах за счет комбинаций обратных связей по переменным АД в замкнутых системах частотного регулирования и можно добиться желаемых или близких к ним свойств электропривода, то в динамических режимах эта задача трудно выполнима. Связано это с весьма сложными электромагнитными процессами, протекающими в АД. Действительно, при любых динамических возмущениях в АД происходит взаимное изменение токов в связанных с ними магнитных потоков машины. При этом скорость изменения магнитных потоков заметно отстает от темпа изменения токов АД. В результате в переходном процессе нарушается взаимосвязь не только абсолютных значений токов и потоков, но и возникает фазовый сдвиг между их векторами. Последний носит свободный и не управляемый в динамике характер. Поскольку и абсолютные значения, и взаимные фазовые сдвиги векторов токов и потоков цепей статора и ротора изменяются одновременно, то при наличии взаимосвязанных звеньев, содержащие электромагнитные постоянные времени цепей статора, контура намагничивания, ротора и механическую постоянную времени ротора, изменение переменных АД во времени будет носить затухающий колебательный характер. Период колебаний и коэффициент их демпфирования зависят от соотношений постоянных времени и абсолютного скольжения АД. После окончания переходного процесса абсолютные значения токов и потоков и фазовые сдвиги между их векторами взаимно сориентируются в пространстве и определяется уже в соответствии с заданным установившимся режимом работы АД. Векторный принцип управления базируется на принудительной взаимной ориентации векторов потокосцеплений и токов АД в полярной или декартовой системах координат в соответствии с заданным законом регулирования. В замкнутых системах векторного управления по цепям обратных связей наряду с абсолютными значениями регулируемых переменных поступает информация о текущем пространственном положении их векторов. За счет регулирования модулей переменных и углов между их векторами обеспечивается полное управление АД как в статике, так и в динамике, обеспечивая тем самым заметное улучшение качества переходных процессов по сравнению со скалярным управлением. Информация о текущих значениях модуля и пространственного положения векторов переменных АД может быть получена как прямым их измерением с помощью соответствующих датчиков, так и косвенно на основе математической модели АД. В общем случае подобные системы с косвенным регулированием координат электропривода из-за нестабильности параметров АД и сложной их взаимосвязи уступают по своим статическим и динамическим показателям системам с прямым векторным управлением. При сложности вычислительных операций и алгоритмов управления электроприводом достоинство систем с косвенным регулированием в простоте технических решений и, соответственно, в практической надежности. Выбранный преобразователь способен работать по любому принципу регулирования. Выбираем бессенсорное векторное регулирование. При этом мы обеспечиваем высокие динамические показатели привода и имеем возможность не использовать тахогенератор, исключая тем самым дополнительную кабельную трассу и эксплуатационные расходы, связанные с содержанием самой кабельной трассы и тахогенераторов. Обратная связь по скорости осуществляется не с тахогенератора, а вычисляется с помощью математической модели двигателя. Обобщенная функциональная схема подобной системы кроме АД и управляемого преобразователя частоты содержит регуляторы и датчики переменных электропривода. Управляющими воздействиями и на входе регуляторов могут быть сигналы задания любых координат электропривода – скорости, угла поворота ротора АД, ток статора, магнитного потока и тому подобное. Возмущающими воздействиям на электропривод могут быть моменты сил сопротивления на валу АД или колебания напряжения питающей сети. Входными сигналами датчиков являются переменные АД, доступные для непосредственного их измерения (частота, напряжение и ток статора, скорость ротора) или определяемые расчетным путем с помощью математической модели АД (ЭДС, потокосцепления статора, ротора и тому подобное). Выходные сигналы регуляторов, зависящие от управляющих воздействий, сигналов обратных связей и принятых алгоритмов регулирования, являются сигналами управления частотой, выходным напряжением и током преобразователя частоты. 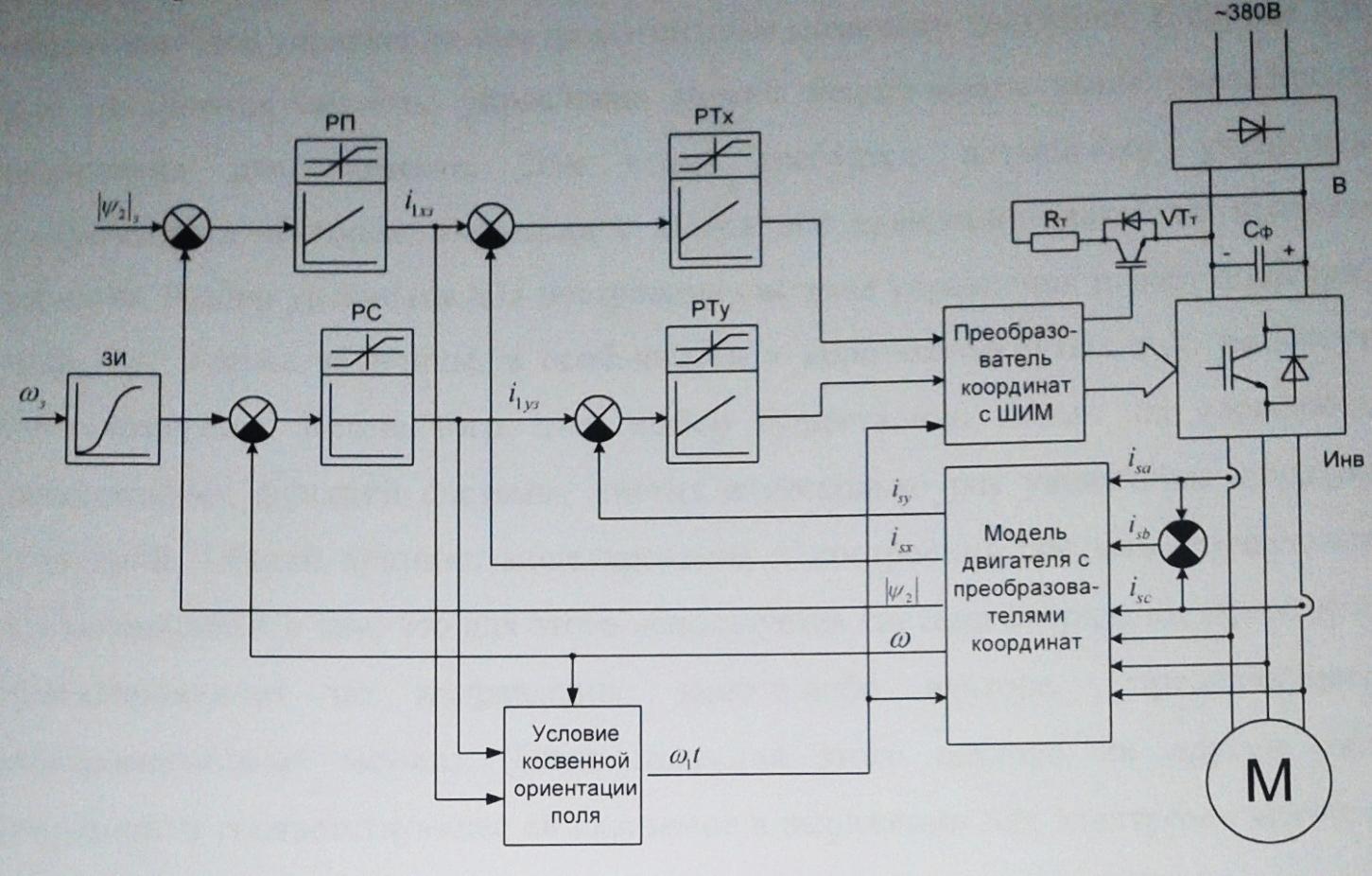 Рис. 1.5. Функциональная схема электропривода Функциональная схема содержит два канала регулирования: потокосцепление с внутренним контуром составляющей тока статора i1x и скорости с внутренним контуром составляющей тока статора i1y. Задание на потокосцепление соответствует номинальному. Задание на скорость поступает через датчик интенсивности, который задает темп разгона привода. Сигналы обратных связей берутся по току и напряжению, далее они поступают в математическую модель двигателя, где вычисляются все необходимые переменные. Момент двигателя 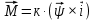 будет определяться векторным произведением любой пары векторов потокосцеплений и токов. Таких пар может быть шесть: будет определяться векторным произведением любой пары векторов потокосцеплений и токов. Таких пар может быть шесть: 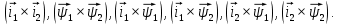 Если в рассмотрение ввести потокосцепление взаимной индукции Если в рассмотрение ввести потокосцепление взаимной индукции 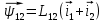 , то появляется еще четыре пары. , то появляется еще четыре пары.Как известно, полная управляемость электропривода обеспечивается, если обеспечивается управление электромагнитным моментом двигателя. В случае АД для построения системы управления можно использовать вышеприведенные выражения для момента. Для этого требуется независимо управлять координатами векторов, входящих в выбранное управление электромагнитного момента. Выбор уравнения для построения системы управления играет большую роль, так как многие величины, в особенности у короткозамкнутых АД, не могут быть измерены. Кроме того, этот выбор существенно влияет на сложность передаточных функций системы, иногда в несколько раз увеличивая порядок уравнений. Общий принцип моделирования и построения системы управления АД заключается в том, что для этого используется система координат, постоянно ориентированная по направлению какого-либо вектора, определяющего электромагнитный момент. Тогда проекция этого вектора на другую ось координат и соответствующее ей слагаемое в выражении для электромагнитного момента будут равны нулю, и формально оно принимает вид, идентичный для выражения электромагнитного момента двигателя постоянного тока, который пропорционален по величине току якоря и основному магнитному потоку. Оптимальным является вариант, когда вещественная ось x ориентирована по вектору потокосцепления ротора. Это позволяет по условию постоянства потокосцепления ротора управлять электромагнитным моментом изменением проекции тока статора на поперечную ось i1y: 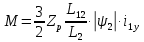 Особое внимание необходимо уделить косвенной ориентации. Как было сказано выше, полная управляемость электропривода обеспечивается, если обеспечивается управление электромагнитным моментом двигателя. А он в первую очередь зависит от потока. Необходимо четко обеспечить косвенную ориентацию вектора потокосцепления ротора по оси x. Структурная схема электропривода В теории и практике применения систем векторного управления наибольшее распространение получили системы, обеспечивающие поддержание потокосцепления ротора 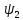 . Такие системы являются более простыми, чем системы, поддерживающие постоянство . Такие системы являются более простыми, чем системы, поддерживающие постоянство 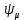 . Поэтому в дальнейшем остановимся на системах, обеспечивающих регулирование . Поэтому в дальнейшем остановимся на системах, обеспечивающих регулирование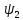 , то есть реализующих закон регулирования , то есть реализующих закон регулирования 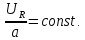 Поскольку модуль вектора потокосцепления ротора определяется проекцией 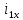 вектора тока статора на ось, связанную с вектором вектора тока статора на ось, связанную с вектором 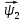 , а электромагнитный момент – произведением модуля потокосцепления ротора на вторую составляющую вектора тока статора, удается построить двухканальную систему регулирования электроприводом с независимым управлением потокосцеплением ротора и электромагнитным моментом двигателя. Структурная схема системы показана на рис.1.6. , а электромагнитный момент – произведением модуля потокосцепления ротора на вторую составляющую вектора тока статора, удается построить двухканальную систему регулирования электроприводом с независимым управлением потокосцеплением ротора и электромагнитным моментом двигателя. Структурная схема системы показана на рис.1.6.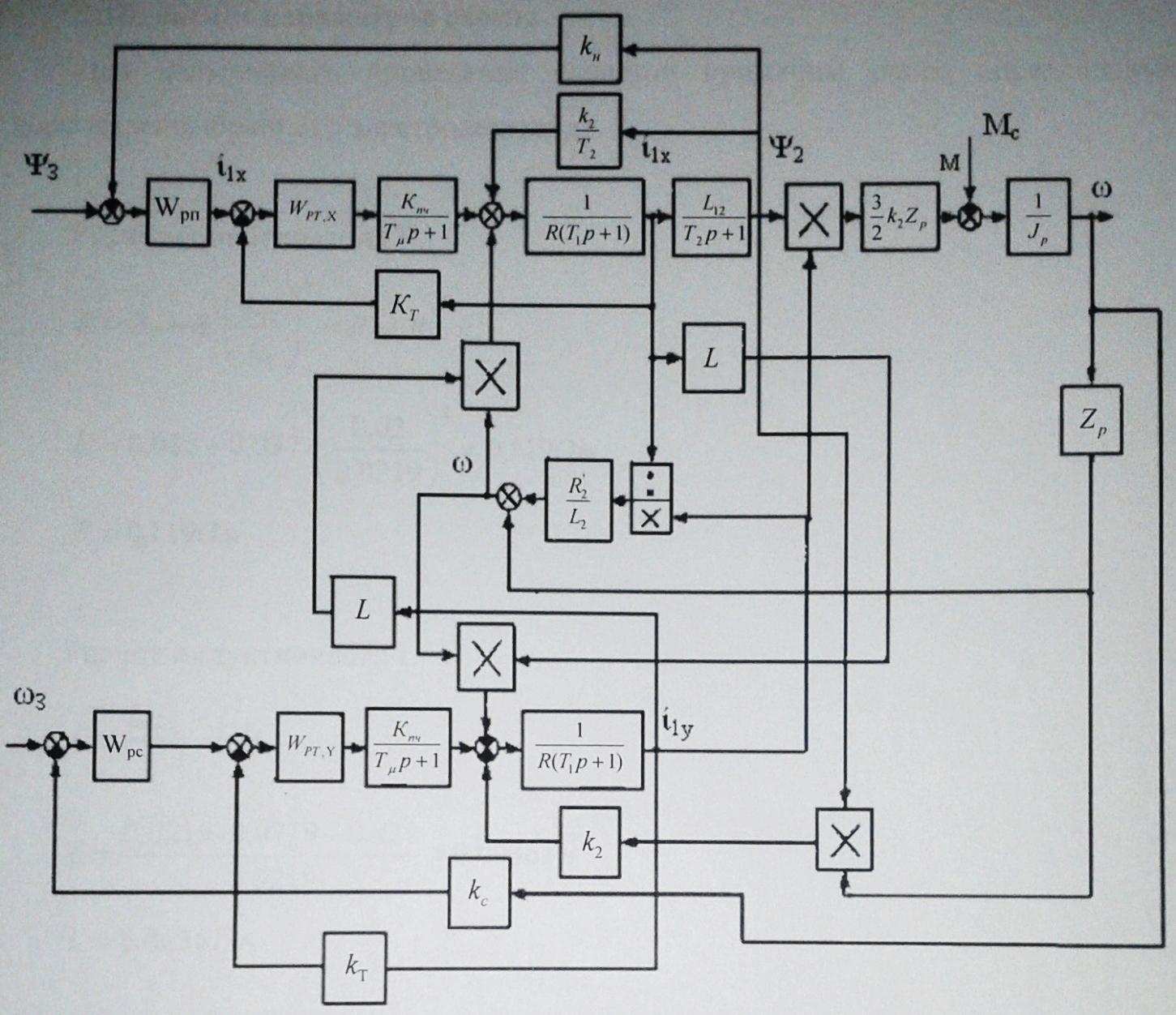 Рис. 1.6. Структурная схема векторного управления Рис. 1.6. Структурная схема векторного управленияКаждый из каналов регулирования строится по принципу подчиненного регулирования в виде двухконтурных подсистем. Система частотно-регулируемого электропривода нелинейна, поэтому аналитический расчет регуляторов может быть выполнен весьма приближенно. Для приближенного синтеза пренебрегаем перекрестными обратными связями, вследствие чего исчезают нелинейности, возникающие при перемножении двух переменных и разных каналов. Чем выше быстродействие регуляторов тока, тем лучше система работает с таким пренебрежением. Окончательная настройка регуляторов производится при наладке электропривода. Расчет параметров схемы Для дальнейшего проведения расчетов применим ранее определенные параметры выбранного электродвигателя. Расчет сопротивления R: 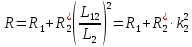 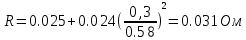 Расчет индуктивности L: 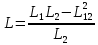 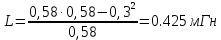 Расчет постоянной времени статорной цепи Т1: 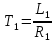 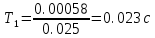 Расчет постоянной времени роторной цепи Т2: 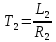 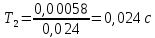 Расчет коэффициента К2: 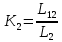 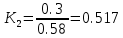 Расчет коэффициента преобразователя частоты 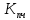 : :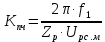 где 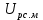 – максимальное значение выходного сигнала РС. В аналоговых системах регулирования – максимальное значение выходного сигнала РС. В аналоговых системах регулирования 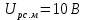 . .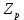 – число пар полюсов. В данном случае – число пар полюсов. В данном случае 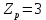 (nн=1000 об\мин). (nн=1000 об\мин).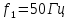 – частота сети. – частота сети.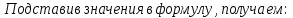 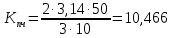 Расчет коэффициента обратной связи по току 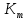 : :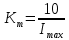 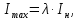 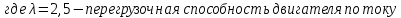 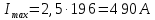 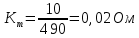 Расчет коэффициента обратной связи по скорости 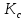 : :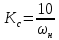 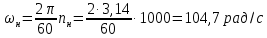 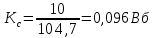 Выбираем постоянную времени 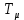 в пределах: 0,002 с≤ в пределах: 0,002 с≤ 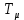 ≤0,02 с. ≤0,02 с.Примем 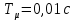 Пренебрегая внутренними перекрестными обратными связями, подсистему регулирования потокосцепления представим в виде схемы: 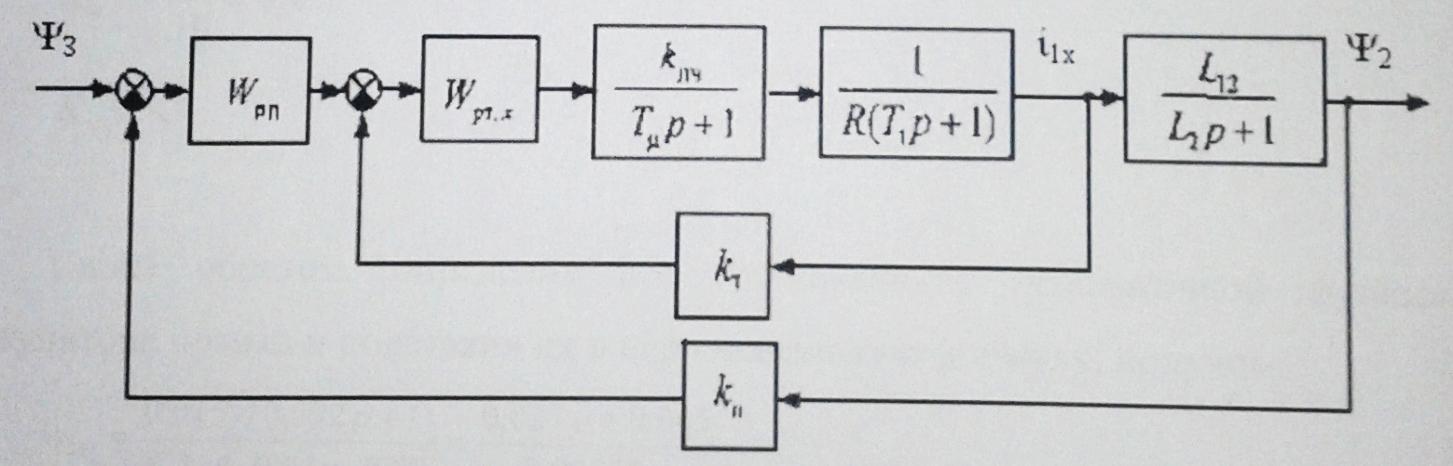 Рис.1.7. Структурная схема канала регулирования потокосцепления ротора Рис.1.7. Структурная схема канала регулирования потокосцепления ротораОпределим передаточную функцию регулятора потока. Передаточная функция регулятора потока имеет вид: 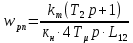 Определение составляющих передаточной функции: Из формулы номинального момента определим номинальное потокосцепление ротора 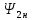 : :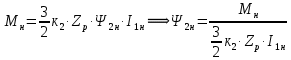 Исходя из формулы 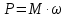 определим номинальный момент: определим номинальный момент: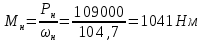 Таким образом: 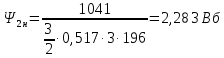 Расчет коэффициента обратной связи по потокосцеплению Кн. 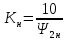 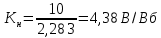 Таким образом, определив все составляющие передаточной функции регулятора потока и подставив их в первоначальную формулу, получим: 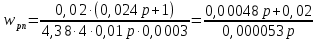 Определим передаточную функцию регулятора тока. Передаточная функция регулятора тока имеет вид: 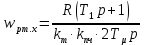 Подставляя все составляющие, определенные ранее, получим: 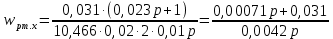 Расчет канала регулирования скорости 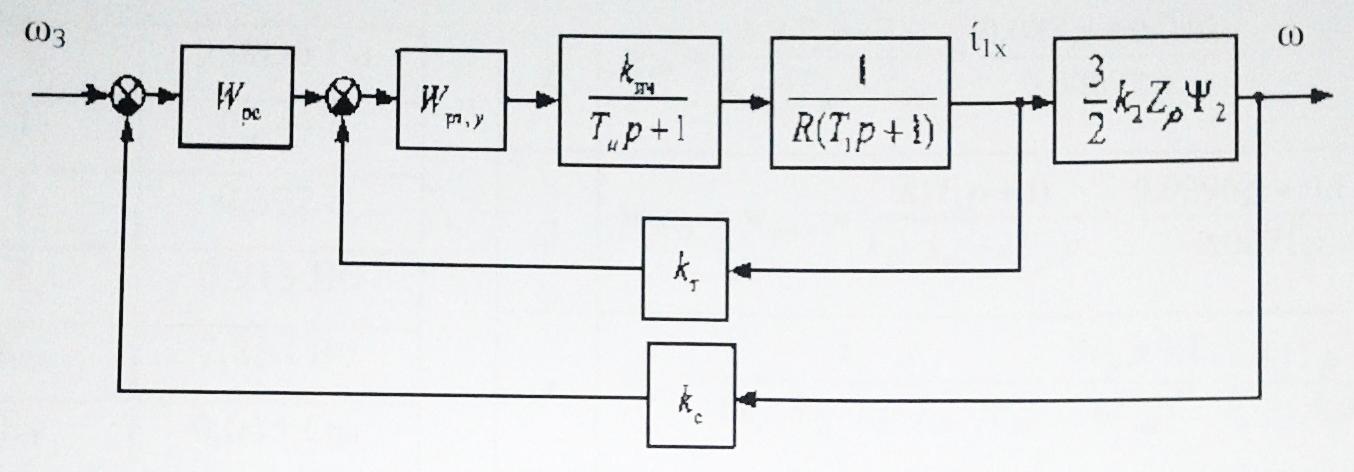 Рис. 2.10. Структурная схема канала регулирования скорости Рис. 2.10. Структурная схема канала регулирования скоростиОпределим передаточную функцию регулятора скорости. Для обеспечения астатизма системы по отношению к нагрузке применим ПИ-регулятор скорости. 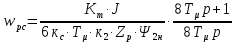 Подставляя все составляющие, определенные ранее, получим: 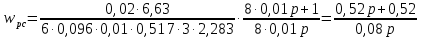 Определим передаточную функцию регулятора тока. Передаточная функция регулятора тока имеет вид: 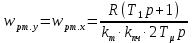 Подставляя все составляющие, определенные ранее, получим: 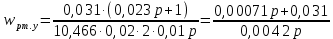 Сведем в табл. 2.2, 2.3 все основные параметры, полученные в процессе расчетов: Таблица 1.2
|
