Документ Microsoft Office Word (2). Контрольная работа 1 5 (а). Определить абсолютное давление воздуха в резервуаре В

• Название: Контрольная работа 1 5 (а). Определить абсолютное давление воздуха в резервуаре В
• Дата: 19.03.2021
• Размер: 1.4 Mb.
• Имя файла: Документ Microsoft Office Word (2).docx
• Тип: Контрольная работа; #186291
• страница: 2 из 3

Ответ: R_x1=R_x2=257,4 кН, h_D=3,665 м.

3.21 (a). Определить величину, линию действия, угол наклона и глубину центра давления равнодействующей h_Dравн на полусферическую крышку в плоской вертикальной стенке закрытого резервуара (рис. 3.21), заполненного бензином.

Принять: радиус полусферы r, показание пьезометра, выведенного на уровне нижней кромки крышки Н, плотность бензина ρ_бенз.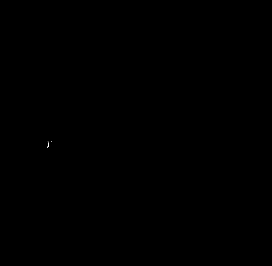





Рисунок 3.21

Решение

Горизонтальная составляющая силы избыточного гидростатического давления бензина на полусферическую крышку равна силе давления на вертикальную проекцию полусферической крышки:

(1)

где - плотность бензина, ;

- расстояние по вертикали от центра тяжести вертикальной проекции крышки до условной свободной поверхности бензина, ;

(2)



- площадь вертикальной проекции полусферической крышки, ;

(3)



тогда по формуле (1)



Сила направлена влево и приложена в центре давления (точка ), который находится на расстоянии эксцентриситета от центра тяжести крышки:

(4)

где - центральный момент инерции плоской стенки относительно горизонтальной оси, ;

(5)

- угол наклона плоской стенки к горизонту;



тогда по формуле (4)



Вертикальная составляющая силы избыточного гидростатического давления бензина на полусферическую крышку:

(6)

где - объем тела давления, .

Для определения вертикальной составляющей силы давления жидкости на полусферическую стенку (рисунок 3.9.1) разделим поверхность стенки горизонтальной плоскостью на верхнюю и нижнюю половины.

Криволинейная поверхность имеет два части - и . Строим тело давления для части . Из контура криволинейной части проводим вертикальные линии до свободной поверхности жидкости, получаем фиктивное (отрицательное) тело давления, построенное на сухой поверхности .

Для части криволинейной поверхности снова проводим вертикальные линии до свободной поверхности и получаем положительное тело давления, так как оно построено на смоченной поверхности и заполнено жидкостью.

Анализ построения двух тел давления показывает, что в объеме два тела давления взаимно уничтожаются (сокращаются или компенсируются).

Результирующее тело давления положительное:

(7)



тогда по формуле (6)



Вектор силы проходит через центр тяжести тела давления. Центр тяжести полукруга находится на расстоянии от диаметра:

(8)



Равнодействующая сила гидростатического давления воды на криволинейную стенку :

(9)



Угол наклона силы к горизонту:

(10)



следовательно, угол .

Линия действия силы пройдет через центр кривизны цилиндрической поверхности, т.е. через центр окружности под углом к горизонту, поскольку в любой точке цилиндрической поверхности гидростатическое давление действует в радиальном направлении

Глубина погружения центра давления: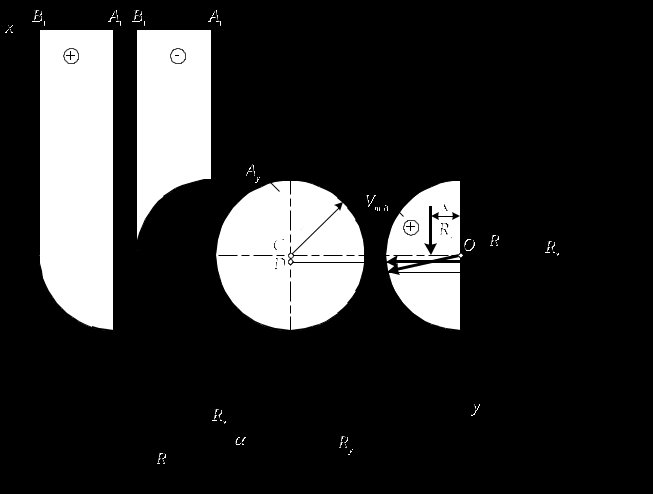

(11)





Рисунок 3.9.1

Ответ: Сила давления бензина R=605,2 Н, угол наклона силы к горизонту α=12º; глубина погружения центра давления у_Dравн.=0,642 м.
4.5 (а). Из бака с постоянным напором вода подается в зумпф, уровень воды в котором также постоянный и ниже оси трубы на величину h (рис. 4.5).

Определить напор воды Н в баке, чтобы расход воды, пропускаемый по трубопроводу диаметром d и длиной l, был равен Q.

Труб водопроводная, чугунная с абсолютной шероховатостью Δ. В системе установлен пробковый кран с углом закрытия α.

Плотность воды ρ=10³ кг/м³; коэффициент кинематической вязкости воды ν=1·10^-6 м²/c.

Вариант
а	2,0	100	80,0	14,0	1,0	30

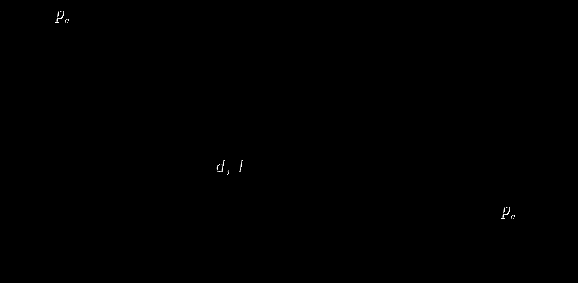Рис. 4.5

Решение

Составляем уравнение Бернулли для сечений 1-1, проходящему по свободной поверхности воды в баке и 2-2, проходящему по свободной поверхности воды в зумпфе, относительно плоскости 2-2 (рис. 4.5.1):

(1)

где , , , , так как сечения проведены через свободные поверхности воды в баке и зумпфе, где скорость движения воды пренебрежимо мала , считая режим движения турбулентным, - суммарные потери напора. В процессе решения задачи режим движения воды будет проверен.

После подстановки всех параметров уравнение Бернулли принимает вид

(2)

откуда находим напор воды в баке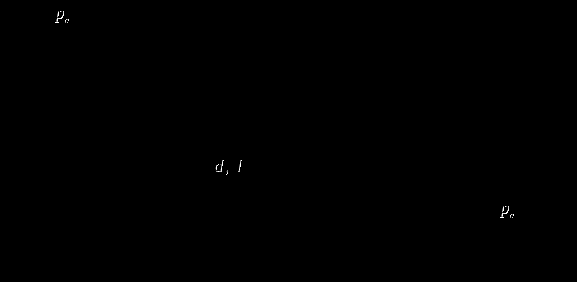

(3)



Рис. 4.5.1

Скорость движения воды в трубопроводе:

(4)



Критерий Рейнольдса:

(5)

где - коэффициент кинематической вязкости воды (справочная величина), ;



так как , то режим течения турбулентный.

Определяем зону гидравлического сопротивления:

- для гидравлических гладких труб:



- для границы области автомодельности:



Так как , то трубопроводы работают в зоне квадратичного сопротивления (IV зона), тогда коэффициент гидравлического трения определяем по формуле Шифринсона:

(6)



Суммарные потери напора в трубопроводе:

(7)

где - длина трубопровода, ;

- коэффициент местного сопротивления при входе в трубу с острыми кромками (справочная величина);

- коэффициент местного сопротивления колена с углом поворота 90º (справочная величина);

- коэффициент местного сопротивления пробкового крана с углом закрытия α=30º (справочная величина);

- коэффициент местного сопротивления при выходе трубы под уровень воды (справочная величина);



Подставляя полученное значение в формулу (3), находим