кр. Вар5. Контрольная работа 1. Элементы линейной алгебры, векторной алгебры, аналитической геометрии и математического анализа. Задание 1
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Контрольная работа №1. Элементы линейной алгебры, векторной алгебры, аналитической геометрии и математического анализа. Задание 1. 3.2.1–3.2.10. Применяя метод Гаусса (метод исключения неизвестных), решить систему линейных уравнений. Сделать проверку. 3.2.25. 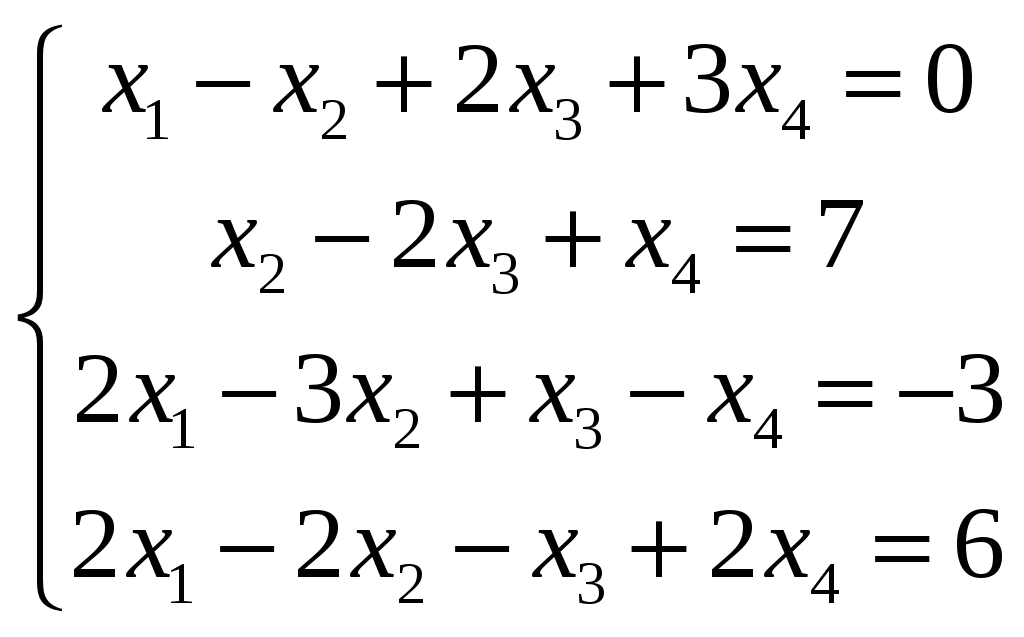 Решение. Вычисления будем производить в таблице. В исходной части таблицы записываем расширенную матрицу системы.
Изменяем третью и четвертую строки: ко третьей строке по элементам прибавляем первую строку, умноженную на (-2), к четвертой– первую строку, умноженную на (-2). В результате получим таблицу.
Изменяем четвертую строку: к четвертой строке по элементам прибавляем вторую строку. В результате получим таблицу.
Изменяем четвертую строку: к четвертой строке, умноженной на (-1) по элементам прибавляем третью строку. В результате получим таблицу.
Делим последнюю строку на (-2):
Так как ранг основной матрицы равен рангу расширенной матрицы, то система совместна. Прямой ход метода Гаусса был пройден при нахождении ранга матриц. Обратный ход метода Гаусса. 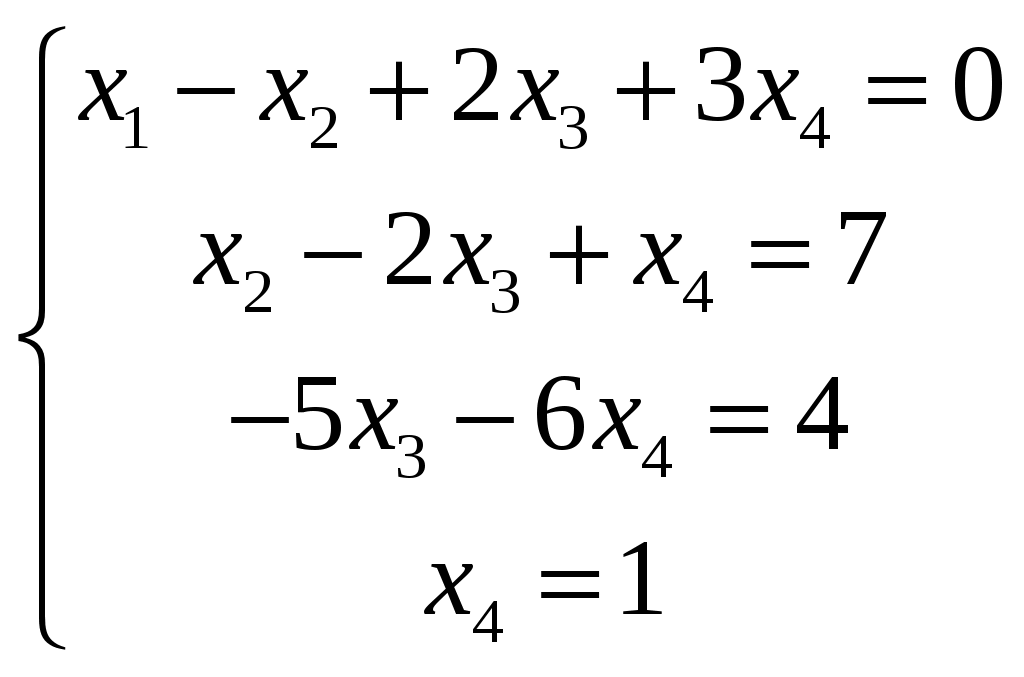 Подставим 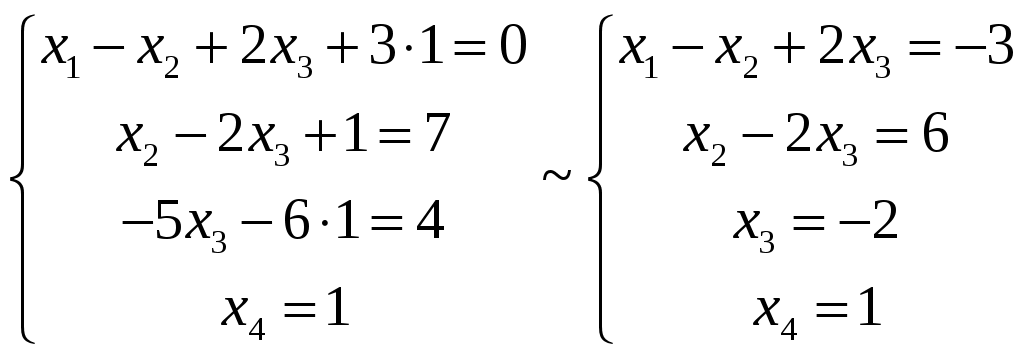 Подставим 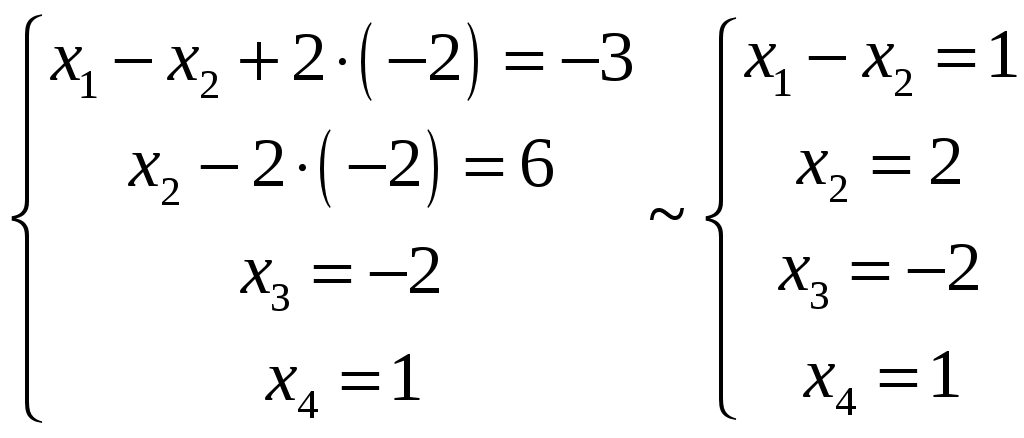 Подставим 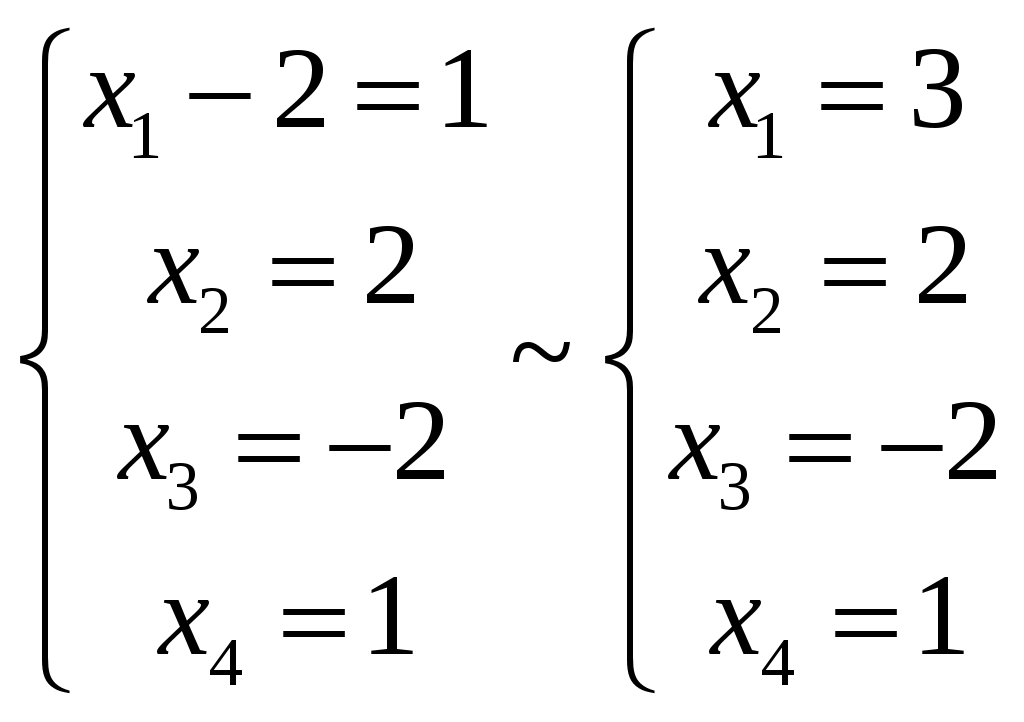 Таким образом, решением системы являются Сделаем проверку, подставляя найденное решение в исходную систему 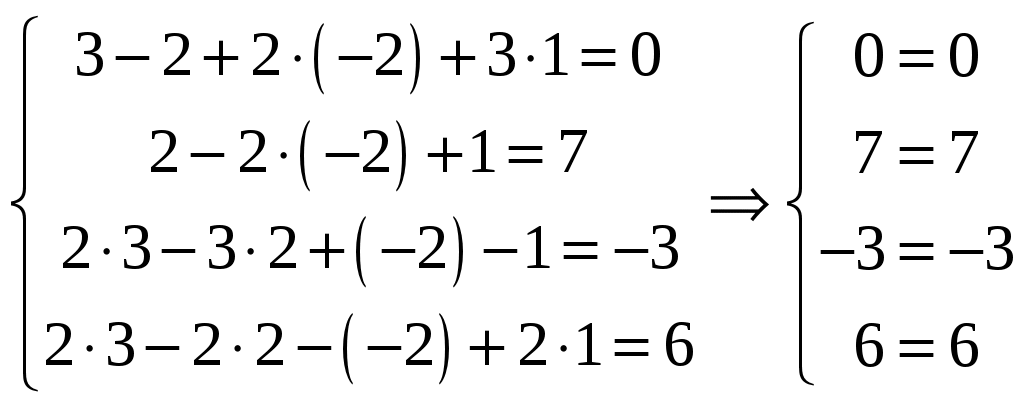 Ответ: Задание 2. 1.1.71–1.1.80. Даны координаты вершин пирамиды 1.1.75. Решение. 1) Угол между прямой 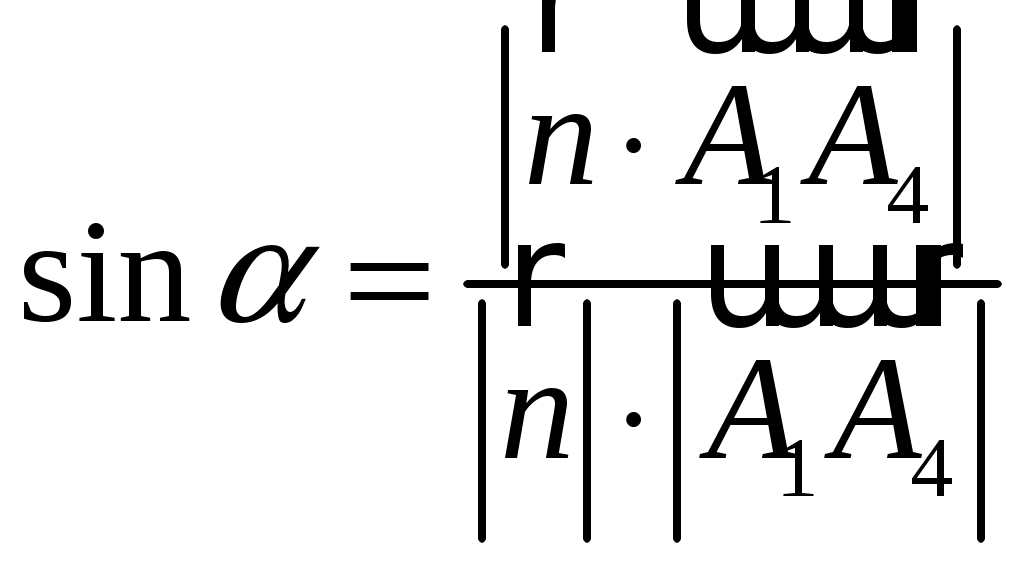 , где , где Составим уравнение плоскости 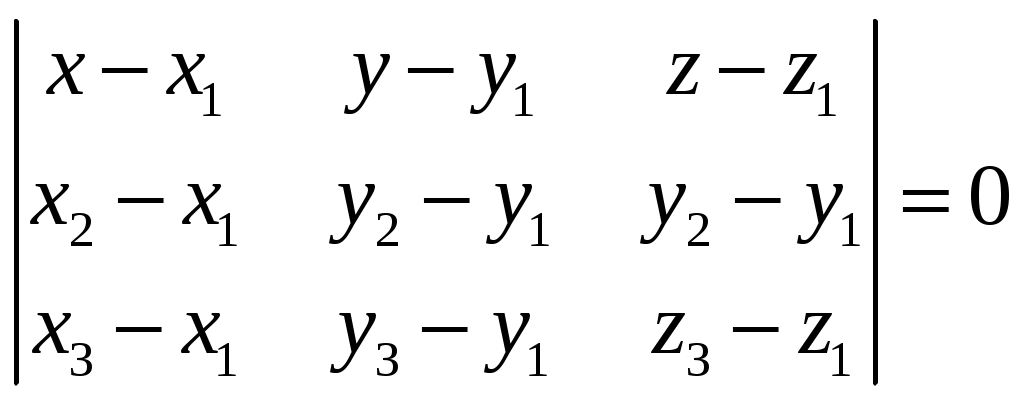 , где , где В нашем случае для плоскости 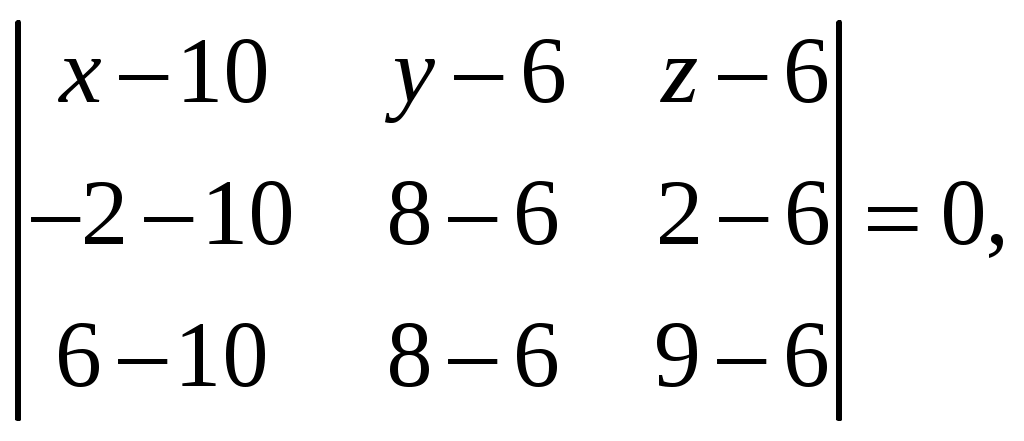 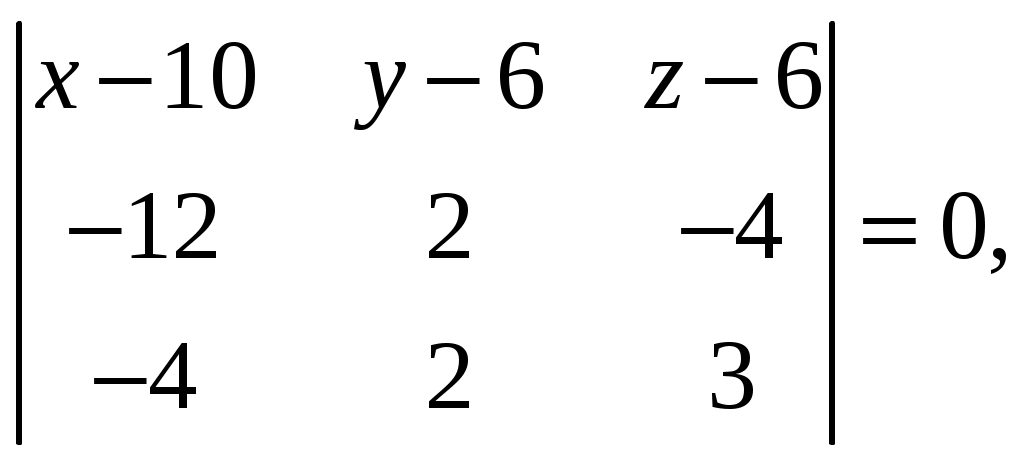 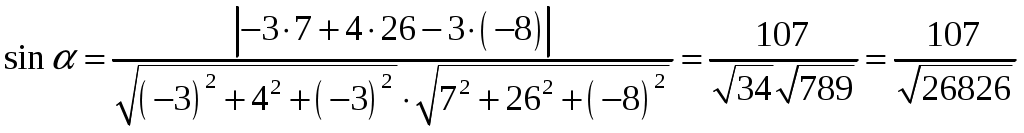 2) Канонические уравнения прямой, проходящей через точку Направляющим вектором высоты, опущенной из вершины Тогда 3) найдено в пункте 1. Делаем чертёж.  Задание 3. 7.3.1–7.3.20. Исследовать методами дифференциального исчисления функцию 7.3.5. Решение. Для полного исследования функции и построения ее графика применяется следующая примерная схема: найти область определения функции; исследовать функцию на непрерывность и определить характер точек разрыва; исследовать функцию на четность и нечетность, периодичность; найти точки пересечения графика функции с осями координат; исследовать функцию на монотонность и экстремум; найти интервалы выпуклости и вогнутости, точки перегиба; найти асимптоты графика функции; по полученным данным построить график функции. Применим вышеуказанную схему для исследования данной функции. Функция определена и непрерывна при всех разрыва у функции нет. 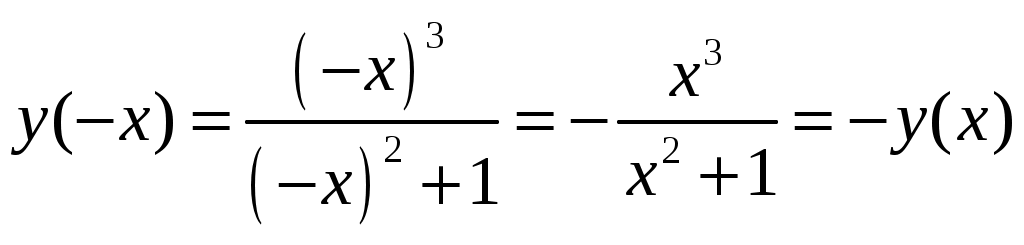 . .Функция является нечетной. Функция не периодическая. С осью Ох: Точка С осью Оу: Точка Находим производную. 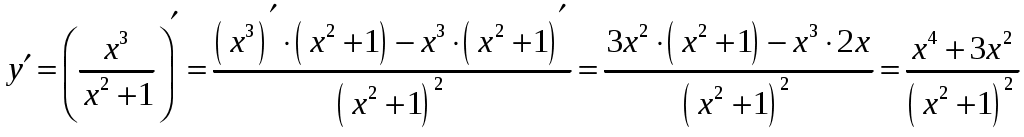 Критическая точка:    + + + +  Функция возрастает на всей области определения, т.к. Находим вторую производную. 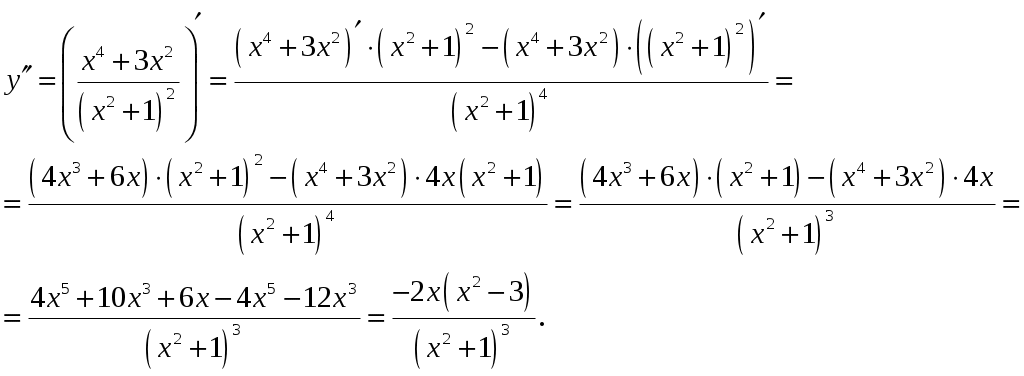      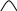 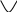  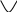 Функция выпукла на интервалах Находим точки перегиба и значения функции в этих точках: Так как точек разрыва нет, то вертикальных асимптот нет. Найдем наклонные асимптоты Вычисляем пределы: 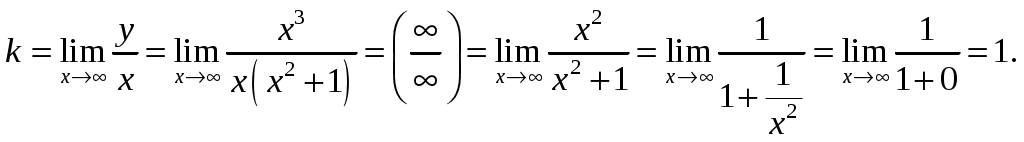 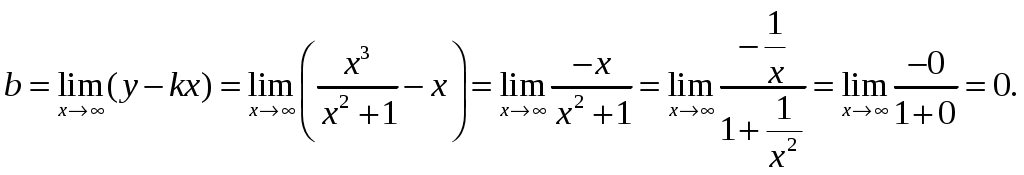 Тогда По полученным данным строим график функции. 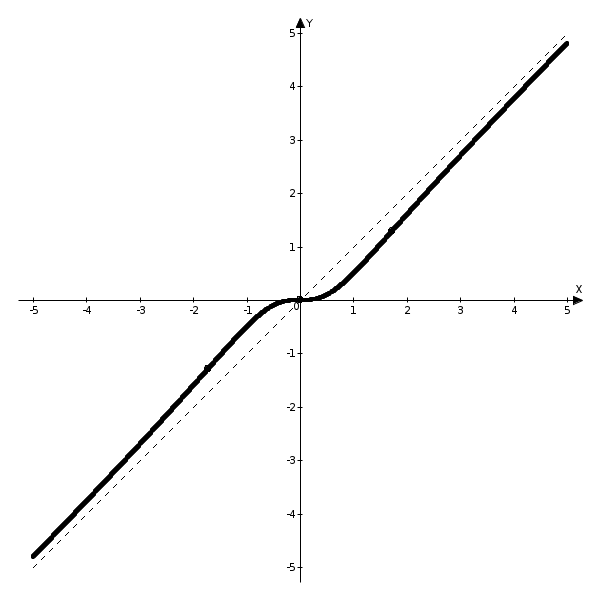 Задание 4. 8.2.61–8.2.70. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж. 8.2.65. Решение. Построим фигуру. 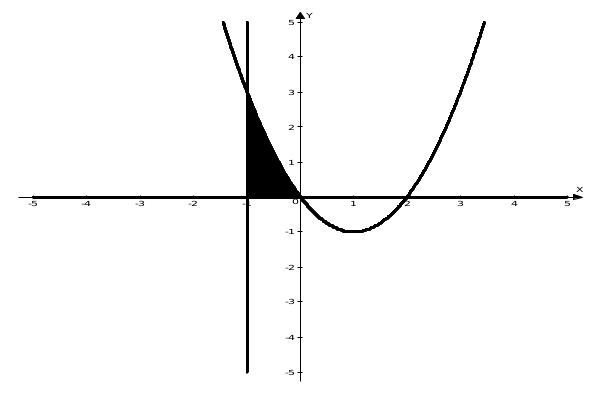 Пределы интегрирования заданы это 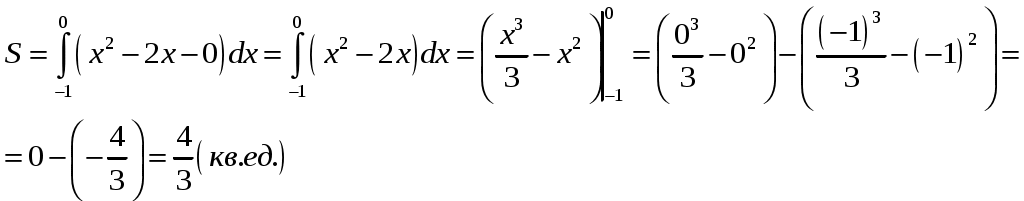 Ответ: Задание 5. 9.2.21-9.2.30. Найти стационарные точки функции F(x, y) и исследовать их на локальный экстремум. 9.2.25. Решение. Найдем частные производные данной функции: Для нахождения точек экстремума, применим необходимое условие локального экстремума дифференцируемой функции: Получаем: Точка Находим выражения: Определяем характер точки экстремума: В точке Тогда Так как Тогда Ответ: |
