Главная страница
Навигация по странице:

  • КОНТРОЛЬНАЯ РАБОТА ЧАСТЬ №1 Вариант 1

  • КОНТРОЛЬНАЯ РАБОТА ЧАСТЬ №2

    		•

    Контр_Физика_1 Б21-731-1з. Контрольная работа 1 механика при выполнении контрольной работы необходимо соблюдать следующие правила


    Скачать 152 Kb.
    НазваниеКонтрольная работа 1 механика при выполнении контрольной работы необходимо соблюдать следующие правила
    Дата11.01.2022
    Размер152 Kb.
    Формат файлаdoc
    Имя файлаКонтр_Физика_1 Б21-731-1з.doc
    ТипКонтрольная работа
    #328094

    ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА № 1

    МЕХАНИКА
    При выполнении контрольной работы необходимо соблюдать следующие правила:

    1. контрольную работу выполнять в тетради или на листах формата А4;

    2. на титульном листе указывать номер контрольной работы, наименование дисциплины, вариант, Ф.И.О. студента.

    3. вариант контрольной работы соответствует последней цифре порядкового номера студента в списке группы;

    4. задачу своего варианта переписывать полностью без сокращений, а заданные физические величины выписать отдельно, при этом все числовые величины должны быть переведены в систему СИ;

    5. для пояснения решения задачи, где это нужно, аккуратно сделать чертеж;

    6. решение задач и используемые формулы должны сопровождаться пояснениями;

    7. в пояснениях к задаче необходимо указывать те основные формулы и законы, на которых базируется решение данной задачи;

    8. при получении расчетной формулы, которая нужна для решения конкретной задачи, обязательно приводить ее вывод;

    9. решение задачи необходимо сначала сделать в общем виде, т. е. только в буквенных обозначениях, поясняя применяемые при написании формул буквенные обозначения;

    10. вычисления следует проводить путем подстановки заданных числовых величин в расчетную формулу. Все числовые значения величин, необходимые для решения данной задачи, должны быть выражены в СИ;

    11. окончательный результат выделить в виде ответа.


    КОНТРОЛЬНАЯ РАБОТА ЧАСТЬ №1
    Вариант 1

    1. Прямолинейное движение точки описывается уравнением м. Найти скорость и ускорение точки в момент времени 2 с, а также среднюю скорость и среднее ускорение за первые две секунды движения.

    2. Колесо, вращаясь равноускоренно, через время 1 мин после начала вращения приобретает частоту 720 об/мин. Найти угловое ускорение колеса и число оборотов колеса за это время.

    3. Тело лежит на наклонной плоскости, составляющей с горизонтом угол 4º. 1) при каком предельном значении коэффициента трения тело начнет скользить по наклонной плоскости? 2) с каким ускорением будет скользить тело по плоскости, если коэффициент трения равен 0.03? 3) сколько времени потребуется для прохождения при этих условиях 100 м пути?

    4. На каком расстоянии от поверхности Земли сила гравитационного притяжения, действующая на тело, в 2 раза меньше, чем у поверхности Земли? Радиус Земли 6,4 Мм.

    5. Камень брошен со скоростью 15 м/с под углом 60° к горизонту. Найдите
      кинетическую, потенциальную и полную энергию камня: а) спустя 1 с после начала движения; б) в высшей точке траектории. Масса камня 0,2 кг. Сопротивлением воздуха пренебречь.

    6. Шар массой 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определите массу большого шара. Удар считать абсолютно упругим, прямым, центральным.

    7. Маховик в форме сплошного однородного диска имеет массу 50 кг и радиус 0,2 м. Он раскручен до 8 об/с и затем предоставлен самому себе. Под влиянием силы трения, приложенной по касательной к ободу, он остановился в течение 50 с. Определить силу трения, считая ее постоянной.

    8. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой 60 кг. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку на платформе? Масса платформы 240 кг. Момент инерции человека рассчитывать, как для материальной точки.

    9. Напишите уравнение гармонического колебательного движения, если максимальное ускорение точки 49.3 см/с2, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.

    10. Определить период колебаний стержня длиной 30 см около оси, перпендикулярной стержню и проходящей через его конец.


    Вариант 2

    1. Движение двух материальных точек выражается уравнениями и , где A1 =20 м, B1 = 3 м/с, C1 = -4 м/с2; A2 =2 м, B2 = 2 м/с, C2 = 0.5 м/с2. В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения в этот момент времени?

    2. Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 об. Какое время прошло с момента выключения вентилятора до полной его остановки.

    3. Тело скользит по наклонной плоскости, составляющей угол 45º. Зависимость пройденного расстояния от времени задается уравнением s=Ct2, где С=1.73 м/с2. Найдите коэффициент трения тела о плоскость.

    4. Каково ускорение свободного падения тела на высоте, равной половине радиуса Земли?

    5. Пружина жесткостью 500 Н/м сжата силой 100 Н. Определите работу внешней силы, дополнительно сжимающей пружину еще на 2 см.

    6. Два шара массами 9 кг и 12 кг подвешены на нитях длиной 1.5 м. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол 30° и отпустили. Считая удар неупругим, определить высоту, на которую поднимутся оба шара после удара.

    7. Кинетическая энергия вала, вращающегося с частотой 5 об/с, 60 Дж. Найти момент импульса L вала.

    8. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой m = 0,5кг. До начала вращения вала высота груза над полом составляла 2.3 м. Определить: 1) время опускания груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол.

    9. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в СИ уравнение гармонических колебаний в виде x = Asin (ωt +φ). Постройте графики, отражающие зависимость проекции скорости vxи проекции ускорения axот времени.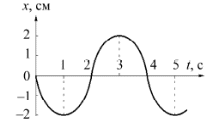



    1. Определить период колебаний диска радиусом 40 см около горизонтальной оси проходящей через образующую диска.


    Вариант 3

    1. Зависимость пройденного телом пути от времени дается уравнением , где м, B = 2 м/с, C= 1 м/с2. Найти среднюю скорость и среднее ускорение за первую, вторую и третью секунды его движения.

    2. Колесо, вращаясь равнозамедленно, за время 1 мин уменьшило свою частоту с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов колеса за это время.

    3. Наклонная плоскость составляет с горизонтом угол 30º. По ней пускают снизу вверх камень, который достигает вершины за 2 с, после чего соскальзывает вниз в течение 4 с. Чему равна длина наклонной плоскости?

    4. Вычислите первую космическую скорость для Луны, если ее радиус равен 1700 км, а ускорение свободного падения тел на Луне 1,6 м/с2.

    5. Тело брошено вертикально вверх со скоростью 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте кинетическая энергия тела будет равна его потенциальной энергии.

    6. Два груза массами 10 кг и 15 кг подвешены на нитях длиной 2 м так, что грузы соприкасаются между собой. Меньший груз отклонили от вертикали на угол 60º и отпустили. Определите высоту, на которую поднимутся оба груза после удара. Удар грузов считать неупругим.

    7. Маховик, момент инерции которого 63.6 кг · м2, вращается с угловой скоростью 31.4 рад/с. Найти момент сил торможения, под действием которого маховик останавливается через время 20 с. Маховик считать однородным диском.

    8. Однородный тонкий стержень массой 0.2 кг и длиной 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через середину стержня. В верхний конец стержня попадает пуля, летящая горизонтально (перпендикулярно к оси вращения) со скоростью 10 м/с и прилипает к стержню. Масса пули 10 г. Определить угловую скорость стержня и линейную скорость нижнего конца стержня сразу после попадания пули.

    9. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в СИ уравнение гармонических колебаний в виде x = Asin (ωt +φ ). Постройте графики, отражающие зависимость проекции скорости vxи проекции ускорения axот времени.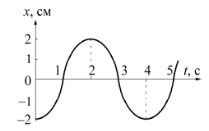



    1. Однородный шарик подвешен на нити, длина которой равна радиусу шарика (l=R=30 см). Определить период колебаний этой системы.



    Вариант 4

    1. Материальная точка движется прямолинейно. Уравнение движения имеет вид x = 3t + 0,06t3. Найти скорость и ускорение точки в моменты времени 5 с и 12 c. Каковы средние значения скорости и ускорения точки за этот интервал времени?

    2. Вал вращается с частотой 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением 3 рад/c2. Через какое время вал остановится? Сколько он сделает оборотов до остановки?

    3. По наклонной плоскости длиной 10 м и высотой 5 м с вершины начинает двигаться тело без начальной скорости. Сколько времени будет продолжаться движение тела до основания наклонной плоскости, если коэффициент трения 0.2? Какую скорость будет иметь тело у основания наклонной плоскости?

    4. Искусственный спутник обращается по круговой орбите на высоте 600 км над поверхностью Земли. Каков период его обращения?

    5. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с. Найти кинетическую и потенциальную энергии камня через 1 с после начала движения. Масса камня 0.2 кг.

    6. Снаряд массой 50 кг, летящий со скоростью 800 м/с под углом 30° к вертикали, попадает в платформу с песком и застревает в нем. Найти скорость платформы после попадания снаряда, если ее масса 16 т.

    7. Две гири с массами 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

    8. Шар и полый цилиндр имеют одинаковую массу (5 кг каждый) и катятся с одинаковой скоростью 10 м/с. Найти кинетические энергии этих тел.

    9. Материальная точка массой 20 г совершает колебания согласно уравнению x = 0,1sin 4πt, м. Найдите силу, действующую в момент времени t = 0.2 с, а также полную энергию точки.

    10. Определить период колебаний диска радиусом 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.



    Вариант 5

    1. Материальная точка движется прямолинейно. Уравнение движения имеет вид x=At+Bt3, где А=6 м/c; B=-0.125 м/c3. Определить среднюю путевую скорость точки в интервале времени от 2 c до 6 c.

    2. Диск, вращаясь вокруг оси, проходящей через его середину, делает 180 об/мин. Определить линейную скорость вращения точек на внешней окружности диска и его радиус, если известно, что точки, лежащие ближе к оси вращения на 8 см, имеют скорость 8 м/с.

    3. Тело массой 5 кг движется по горизонтальной поверхности под действием горизонтально направленной силы 100 Н. Определить ускорение тела, если известно, что коэффициент трения между телом и поверхностью равен 0.2.

    4. Средняя плотность Венеры 4900 кг/м3, а радиус планеты 6200 км. Найдите ускорение свободного падения на поверхности Венеры.

    5. Гиря, положенная на верхний конец спиральной пружины, поставленной вертикально на подставке, сжимает ее на 2 мм. На сколько сожмет пружину та же гиря, если она упадет на конец пружины с высоты 5 см?

    6. Лодка длиной 3 м и массой 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами 60 кг и 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

    7. Маховое колесо, момент инерции которого 245 кг · м2, вращается с частотой 20 об/с. Через время 1 мин после того, как на колесо перестал действовать момент сил, оно остановилось. Найти момент сил трения и число оборотов, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.

    8. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара равна 14 Дж. Определите кинетическую энергию поступательного и вращательного движения шара.

    9. Уравнение колебания тела массой 2 кг имеет вид х = 5cos[π(t + 0.1)], см. Определите потенциальную энергию в момент времени t = 5 с.

    10. Обруч диаметром 60 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний.



    Вариант 6

    1. Тело брошено с башни вертикально вверх со скоростью 10 м/с. Высота башни 2,5 м. Написать уравнение движения тела и определить среднюю путевую скорость с момента бросания до момента падения на землю.

    2. Колесо радиусом 0,1 м, вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость, 2) угловое ускорение, 3) нормальное ускорение.

    3. Маневровый тепловоз массой 100 т тянет два вагона массой 50 г каждый с ускорением 0.1 м/с2. Найдите силу тяги тепловоза, если коэффициент сопротивлению движению 0.006.

    4. Среднее расстояние между центрами Земли и Луны равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли. На каком расстоянии от центра Земли тело будет притягиваться к Земле и Луне с одинаковыми силами? Радиус Земли 6400 км.

    5. Тело массой 1 кг движется под действием некоторой силы согласно уравнению х=А-Bt+Ct2-Dt3, где B=3 м/с, C=5 м/с2, D=1 м/с3. Определите максимальную мощность, затрачиваемую на движение тела за время, равное 1 с.

    6. Тело массой 0,5 кг бросают со скоростью 10 м/с под углом 30° к горизонту. Пренебрегая сопротивлением воздуха, определить кинетическую, потенциальную и полную энергии тела: 1) через 0.4 с после начала движения; 2) в высшей точке траектории.

    7. Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через блок массой m =1 кг. Найти ускорение а, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

    8. Катящийся цилиндр массой 2 кг остановлен силой 9.81 Н на пути 0,5 м. Вычислить скорость цилиндра до торможения.

    9. Определить максимальное ускорение материальной точки совершающей гармонические колебания с амплитудой 15 см, если наибольшая скорость точки 30 см/c. Написать уравнение колебаний.

    10. Однородный стержень длиной 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей на расстоянии 10 см от его верхнего конца. Определите период колебаний стержня.


    Вариант 7

    1. Тело падает с высоты 20 м с нулевой начальной скоростью. Какой путь пройдет тело за первую и последнюю секунду своего падения?

    2. Колесо радиусом 10 см вращается по закону: φ = 8t – t2. Найти нормальное и тангенциальное ускорение точек на ободе колеса через 2 с от начала движения.

    3. Трамвай, трогаясь с места, движется с ускорением 0.5 м/с2. Через время 12 с после начала движения мотор выключается и трамвай движется до остановки равнозамедленно. Коэффициент трения на всем пути 0.01. Найдите время движения трамвая с момента выключения мотора до остановки. Какой путь пройдет трамвай за все время движения?

    4. Какую скорость должен иметь искусственный спутник, чтобы обращаться по круговой орбите на высоте 600 км над поверхностью Земли? Радиус Земли 6400 км.

    5. Пуля массой 15 г, летящая горизонтально со скоростью 200 м/с, попадает в баллистический маятник длиной 1 м и массой 1.5 кг и застревает в нем. Определить угол отклонения маятника.

    6. Материальная точка массой 1 кг двигалась под действием некоторой силы согласно уравнению s = A– Bt+ Ct2 –Dt3 (В = 3 м/с, С = 5 м/с2, D= l м/с3). Определить мощность, затрачиваемую на движение точки в момент времени 1 с.

    7. Частота вращения маховика, момент инерции которого равен 120 кг·м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время π мин. Считая трение в подшипниках постоянным, определить момент сил трения.

    8. Обруч и диск одинаковой массы катятся без скольжения с одной и той же скоростью υ. Кинетическая энергия обруча 40 Дж. Найти кинетическую энергию диска.

    9. Математический маятник массой 10 г колеблется согласно уравнению x=5cos(πt/3+π/4). Найти длину маятника, максимальную силу, действующую на него и его полную механическую энергию.

    10. Амплитуда затухающих колебаний маятника за 1 мин уменьшилась вдвое. Во сколько раз она уменьшится за 4 мин?

    Вариант 8

    1. Материальная точка движется прямолинейно. Уравнение движения имеет вид , где A = 3 м/с, B = 0.06 м/с3. Найти скорость и ускорение точки в момент времени и с.

    2. Диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A+Вt+Ct2+Dt3 (В = 1 рад/с, С = 1 рад/с2, D= 1 рад/с3). Определить для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение; 2) нормальное ускорение; 3) полное ускорение.

    3. Чему равен вес груза, массой 200 кг при равноускоренном подъеме его в лифте, если известно, что лифт достиг скорости 4 м/с, пройдя путь 20 м?

    4. Ракета поднялась на высоту 1500 км. Как изменилась сила тяжести, действующая на ракету, на этой высоте по сравнению с силой тяжести у поверхности Земли? Радиус Земли 6400 км.

    5. Автомашина массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути. Определить: 1) работу, совершаемую двигателем автомашины на пути 5 км, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.

    6. Определить, во сколько раз уменьшится скорость шара, движущегося со скоростью υ1, при его соударении с покоящимся шаром, масса которого в n раз больше массы налетающего шара. Удар считать центральным абсолютно упругим.

    7. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определять, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

    8. Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением 0.4 рад/с2. Определить кинетическую энергию маховика через время 25 с после начала движения, если через 10 с после начала движения момент импульса маховика составлял 60кг·м2/с.

    9. Амплитуда гармонических колебаний материальной точки 2 мм, полная энергия колебаний = 2·10–7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 10–6 Н?

    10. Диск радиусом 48 см колеблется около горизонтальной оси, проходящей на расстоянии 36 см от оси диска перпендикулярно к плоскости диска. Определите частоту колебаний такого физического маятника.


    Вариант 9

    1. Какой путь пройдет тело до полной остановки и сколько времени длится движение, если изменение его скорости задано уравнением: V=40-2t м/с?

    2. Точка движется по окружности радиусом 10 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 10 с после начала движения, если известно, что к концу 10 оборота после начала движения угловая скорость точки равна 100 рад/с.

    3. Лифт опускается равноускоренно и за первые 10 с проходит путь 10 м. Насколько уменьшится вес пассажира массой 70 кг, который находится в этом лифте?

    4. Спутник планеты обращается по орбите радиусом 9.4·106 м с периодом 7 ч 39 мин. Определите массу планеты.

    5. Тело массой m= 5 кг поднимают с ускорением 2 м/с2. Определить работу силы в течение первых пяти секунд.

    6. Тело массой 5 кг движется со скоростью 4 м/с и сталкивается неупруго с телом массой 4 кг, движущимся со скоростью 2 м/с. Какое количество теплоты выделится при ударе, если тела до удара: а) двигались в одном направлении? б) навстречу друг другу?

    7. Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Работа сил торможения равна 44.4 Дж. Найти момент инерции вентилятора и момент сил торможения.

    8. Человек массой 60 кг, стоящий на краю горизонтальной платформы радиусом  1 м массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру.

    9. Найдите амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями x1 = 0.02sin(5πt + π/2), м, и х2 = 0,03sin(5πt + π/4), м.

    10. Один математический маятник имеет период 3 с, а другой 4 с. Каков период колебаний математического маятника, длина которого равна сумме длин указанных маятников?



    Вариант 0

    1. Мяч брошен со скоростью 10 м/с под углом 30˚ к горизонту. Какое время мяч будет в движении? Какова дальность полета мяча? На какую высоту поднимется мяч?

    2. Колесо вращается с постоянным угловым ускорением 3 рад/с2. Определить радиус колеса, если через 1 с после начала движения полное ускорение колеса 7,5 м/с2.

    3. Летчик массой 70 кг описывает на самолете «мертвую петлю» радиусом 100 м. Скорость самолета 180 км/ч. Найдите вес летчика в верхней и нижней точках петли.

    4. Определите первую космическую скорость для Венеры. Масса Венеры 4,87·1024 кг, радиус 6.05·106 м.

    5. Найти работу, которую надо совершить, чтобы на пути 10 м увеличить скорость движения тела массой 1 кг от 2 м/с до 6 м/с. На всём пути действует постоянная сила трения 2 Н.

    6. Платформа с песком общей массой 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой 8 кг и застревает в нем. Пренебрегая трением, определить, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда 450 м/с, а ее направление — сверху вниз под углом 30° к горизонту.

    7. Шар массой 200 г, движущийся со скоростью 10 м/с, ударяет неподвижный шар массой 800 г. Удар прямой, абсолютно упругий. Каковы будут скорости шаров после удара?

    8. Маховик вращается с частотой 10 об/с. Его кинетическая энергия 7.85 кДж. За какое время момент сил 50 Н · м, приложенный к маховику, увеличит угловую скорость маховика вдвое?

    9. Уравнение движения точки дано в виде x = sin 6πt, см. Найдите моменты времени, в которые достигается максимальная скорость и максимальное ускорение.

    10. Однородный стержень длиной 1 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей на расстоянии 10 см от его верхнего конца. Определите период колебаний стержня.

    КОНТРОЛЬНАЯ РАБОТА ЧАСТЬ №2
    Вариант теоретических вопросов соответствует последней цифре порядкового номера студента в списке группы.

    1. Номера вопросов приведены в таблице.

    2. Ответы на вопросы даются достаточно подробно в письменном виде.


    Таблица 2. Варианты теоретических вопросов.


    Вариант
    Вопрос №1
    Вопрос №2

    1
    1
    11

    2
    2
    12

    3
    3
    13

    4
    4
    14

    5
    5
    15

    6
    6
    16

    7
    7
    17

    8
    8
    18

    9
    9
    19

    0
    10
    20



    Вопросы:



    1. Система отчета. Траектория, путь, вектор перемещения, скорость (средняя и мгновенная).

    2. Нормальное, тангенциальное и полное ускорение.

    3. Кинематические характеристики вращательного движения: угловое перемещение, угловая скорость и угловое ускорение.

    4. Связь угловых характеристик с линейными.

    5. Закон инерции. Инерциальные и неинерциальные системы отсчета.

    6. Физическое содержание понятий массы, силы, импульса, импульса силы.

    7. 2-ой закон Ньютона. 3-ий закон Ньютона.

    8. Внешние и внутренние силы. Закон сохранения импульса для замкнутой системы тел.

    9. Понятие центра масс и закон его движения.

    10. Понятие работы и мощности. Кинетическая энергия механической системы.

    11. Понятие потенциального поля. Потенциальная энергия материальной точки во внешнем силовом поле и её связь с силой, действующей на материальную точку.

    12. Консервативные и неконсервативные силы. Закон сохранения энергии в механике.

    13. Применение законов сохранения к упругому и неупругому ударам.

    14. Динамические характеристики вращательного движения: момент силы, момент импульса, момент инерции.

    15. Вычисление моментов инерции тел правильной формы. Теорема Штейнера.

    16. Основной закон динамики вращательного движения в векторной и скалярной формах. Закон сохранения момента импульса.

    17. Кинетическая энергия и работа во вращательном движении.

    18. Колебательное движение. Гармоническое колебание и его характеристики Скорость и ускорение при гармонических колебаниях.

    19. Динамика гармонических колебаний. Дифференциальное уравнение гармони­ческих колебаний. Пружинный, математический и физический маятник.

    20. Затухающие колебания. Дифференциальное уравнение затухающих колебаний, его решение и анализ

    написать администратору сайта