Высшая математика. Контрольная работа 1 Найти объем пирамиды, построенной на векторах,. Сделать чертеж. Решение (ед 3 )
 Скачать 142.58 Kb.
|
|
Контрольная работа №1 9. Найти объем пирамиды, построенной на векторах: 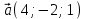 ,  ,  . Сделать чертеж.Решение   (ед3) Ответ: 10,67 ед3 19. Даны уравнения двух медиан треугольника х-2у+1=0 и у-1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж. Решение. Пусть т.В имеет координаты (х1;у1), т.к. точка К по условию есть середина отрезка АВ, то ее координаты равны  и удовлетворяют уравнению х-2у+1=0, то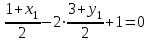 . Кроме того координаты точки В(х1;у1) удовлетворяют уравнению у-1=0, получаем систему линейных алгебраических уравнений 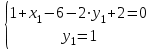  , т.В(5;1)Аналогично найдем координаты точки С(х2;у2). Пусть N – середина отрезка АС, тогда координаты точки находятся по формулам  ,  т.С(-3,-1)Уравнение АВ:  или  или х+2у-7=0 (АВ)Уравнение ВС:  или  или х-4у-1=0 (ВС)Уравнение АС:  или 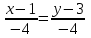 или х-у+2=0 (АС)  В К А N С 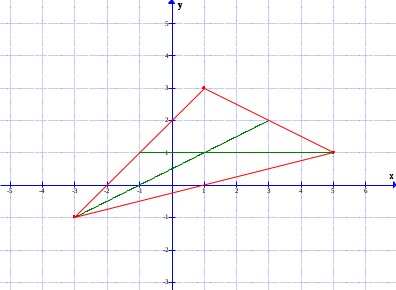 Ответ: х-у+2=0 (АС), х-4у-1=0 (ВС), х+2у-7=0 (АВ) 29. Систему линейных уравнений решить методом Гаусса (методом исключения неизвестных). Сделать проверку.  Решение. Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду.  =[ Поменяем местами первую и вторую строчки]= =[умножим первую строку на -2 и сложим со второй, умножим первую строку на -3 и сложим с третьей]= =[умножим вторую строку на -4, третью на 3 и сложим их]= Решаем систему уравнений  Получаем х1=1 х2=1 х3=-1 Сделаем проверку, подставляем решения в исходную систему  Ответ: х1=1 х2=1 х3=-1 39. Найти пределы функций, не пользуясь правилом Лопиталя. а)  б)  в) 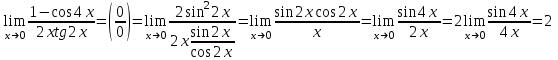 г) 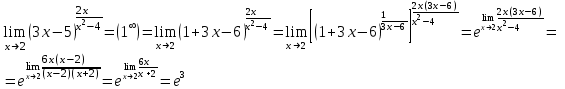 49. Найдите производные  данных функций.а)   б)  при t=2  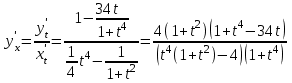  в)   59. Методами дифференциального исчисления исследовать функцию  для  и по результатам исследования построить ее график;Решение. Область определения функции  функция непрерывнаТочки пересечения с осями координат: Ох: 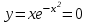 при  , получаем точку О(0;0) Оу: х=0 y=0 т.(0; 0) – точка пересечения. Функция является нечетной, т.к.  Экстремумы и монотонность. Вычисляем первую производную  Находим критические точки  при х=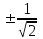
Выпуклость и точки перегиба. Вычислим вторую производную  Найдем точки перегиба  при х=0
наклонные асимптоты вида у=kx+b   Прямая у=0 – горизонтальная асимптота 7  . Строим график функции:69. Найти производные функции двух переменных  |
)
)
