Главная страница
Навигация по странице:

  • Контрольная работа № 1 по дисциплине Дискретная математика Закончить обзорТест начат

  • Оценка

  • © 4

  • ж 3 ; (ж

  • = (ж!ж 3 ); (ж

    		•

    Контрольная. Контрольная работа № 1 ответы'. Контрольная работа 1 по дисциплине 'Дискретная математика' Закончить обзор Тест начат Суббота 5


    Скачать 77.42 Kb.
    НазваниеКонтрольная работа 1 по дисциплине 'Дискретная математика' Закончить обзор Тест начат Суббота 5
    АнкорКонтрольная
    Дата30.01.2022
    Размер77.42 Kb.
    Формат файлаdocx
    Имя файлаКонтрольная работа № 1 ответы'.docx
    ТипКонтрольная работа
    #346307
    страница1 из 3
      1   2   3





    Правила выполнения теста Учебный план
    ►Контрольная работа № 1 по дисциплине 'Дискретная математика'
    Закончить обзор
    Тест начат

    Суббота 5 Декабрь 2020, 15:01

    Завершен
    Суббота 5 Декабрь 2020, 17:22

    Прошло времени
    2 ч 21 мин

    Правильных
    9/20

    ответов из



    Оценка
    45 из максимума 100 (45%)

    Результат






    Незачет


    1

    Упростите булеву формулу f(x, y, z) = x(-y v z)(-x v y v z).

    f(x, y, z) = z □ f(x, y, z) = -y v z f(x, y, z) = xz

    Верно




    В графе (см. рисунок) задано паросочетание, выделенное «жирными рёбрами».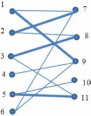



    Для увеличения паросочетания выделите в данном графе тонкую чередующуюся цепь.

    Тонкая чередующаяся цепь включает рёбра: (10, 5), (5, 11), (11, 3), (3, 8), (8, 2), (2, 7), (7, 1).

    □ Тонкая чередующаяся цепь включает рёбра: (4, 9), (9, 1), (1, 7), (7, 2), (2, 8), (8, 3), (3, 11),

    (11, 5), (5, 10).

    Тонкая чередующаяся цепь включает рёбра: (7, 1), (1, 9), (9, 4).

    Верно

    ©




    4

    Найдите все максимальные пустые подграфы в графе G(X,U)     где и = {(Ж1Ж2), (ж3ж4), (ж3ж2), (ж!жз), (жТж4 )}•

    S = х\\ ж3; (ж2ж3)

    5 = ®i; Ж4

    S = (Ж2Ж4)

    Неверно

    Выберите все верные ответы (может быть несколько или один).
    Найдите все максимальные пустые подграфы в графе G(X,U)     где U = {(Ж1Ж2), (ж3Ж4), (х3Х2), (ж!жз ), (Ж1Ж4), (®2®4 )}•

    5 = (ж!ж3); (ж2ж4); (Ж3Ж4); (х2хг) 5 = (Ж2Ж4)

    S' = ®i; ж4; ж2; ж3

    Неверно

    СП




    Граф G = (X, U) задан матрицей инцидентностей B.
    B

    u1
    u2
    u3
    u4
    u5
    u6

    1
    1
    0
    1
    0
    0
    1

    2
    1
    1
    0
    0
    0
    0

    3
    0
    0
    0
    0
    1
    1

    4
    0
    0
    0
    1
    1
    0

    5
    0
    1
    1
    1
    0
    0


    Если граф G содержит эйлерову цепь, то укажите её концевые вершины.
    1; 5

    • Таких вершин нет, т.к. данный граф не содержит эйлерову цепь
      5; 2

    • 4; 3

    Неверно



    Выберите все верные ответы (может быть несколько или один).
    6

    Выберите все верные ответы (может быть несколько или один).




    Решите задачу с помощью диаграмм Эйлера-Венна (см. рисунок).




    На полу комнаты площадью 24 м2 лежат три ковра. Площадь одного из них - 8 м2, другого - 10 м2, третьего - 6 м2 Каждые два ковра перекрываются по площади 3 м2, а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м2 Найдите площадь участка пола:

    а) покрытого первым и вторым коврами, но не покрытого третьим ковром;

    б) покрытого только первым ковром;

    в) непокрытого коврами.
    а) 10 м2; б) 3 м2; в) 8 м2






    а) 10 м2; б) 5 м2; в) 6 м2






    а) 3 м2; б) 5 м2; в) 1 м2




    Верно



    B
    1
    2
    3
    4
    5
    6
    7

    1
    0
    2
    1
    0
    1
    0
    0

    2
    2
    0
    0
    0
    1
    1
    0

    3
    1
    0
    0
    1
    0
    0
    0

    4
    0
    0
    1
    0
    1
    0
    0

    5
    1
    0
    0
    1
    0
    0
    1

    6
    0
    1
    0
    0
    0
    0
    1

    7
    0
    0
    0
    0
    1
    1
    0

    Фтах
    = 40

    Фтят
    = 44

    Фтят
    = 22

    Фтят
    = 65


    Неверно
      1   2   3

    написать администратору сайта