Контрольная. Контрольная работа № 1 ответы'. Контрольная работа 1 по дисциплине 'Дискретная математика' Закончить обзор Тест начат Суббота 5

• Название: Контрольная работа 1 по дисциплине 'Дискретная математика' Закончить обзор Тест начат Суббота 5
• Анкор: Контрольная
• Дата: 30.01.2022
• Размер: 77.42 Kb.
• Имя файла: Контрольная работа № 1 ответы'.docx
• Тип: Контрольная работа; #346307
• страница: 2 из 3

©

Выберите все верные ответы (может быть несколько или один).

9

На основании таблицы истинности бинарных операций определите ДНФ операции x-| | x2.

-x-,^ v x2-x-|

Q -x<| v -x2

-x1 -x2 v -x^x2 v x<|-x2

Верно




Выберите все верные ответы (может быть несколько или один).







В графе (см. рисунок) задано паросочетание, выделенное «жирными рёбрами».




Для увеличения паросочетания выделите в данном графе тонкую чередующуюся цепь.

• 
  Тонкая чередующаяся цепь включает рёбра: (10, 5), (5, 11).
  

Q Тонкая чередующаяся цепь включает рёбра: (4, 9), (9, 1), (1, 7), (7, 6).

• 
  Тонкая чередующаяся цепь включает рёбра: (2, 7), (7, 1), (1, 9).
  

Неверно

Найдите все максимальные пустые подграфы в графе G(X, U) где U = {(Ж1Ж₂), (ж₃ж₄), (ж₃ж₂), (Ж1Ж₃), (Ж1Ж4), (ж₂ж₄)}.

S = ®i; x4; x2; x3 S = ®i; ж3; (ж2ж3) CD Выберите все верные ответы (может быть несколько или один). 12 Граф G = (X, U) задан матрицей смежности R. R	1	2	3	4	5	6	7	8	9	10
1	0	2	1	0	1	0	0	0	0	0
2	2	0	0	0	1	1	0	0	0	0
3	1	0	0	1	0	0	0	0	0	0
4	0	0	1	0	2	0	0	0	0	0
5	1	1	0	2	0	0	1	0	0	0
6	0	1	0	0	0	0	1	1	0	1
7	0	0	0	0	1	1	0	1	2	1
8	0	0	0	0	0	1	1	0	0	0
9	0	0	0	0	0	0	2	0	0	0
10	0	0	0	0	0	1	1	0	0	0

Определите, содержит ли граф G эйлерову цепь.		Содержит, т.к. есть вершины с нечётными степенями.
		Содержит, т.к. количество вершин с нечётными степенями равно двум.

Выберите все верные ответы (может быть несколько или один).

После пропускания потока в транспортной сети (см. рисунок) насыщенными оказались дуги: U = (1,

3), (5, 3), (5, 6), (2, 6), (2, 4), (4, t), (3, t), (6, t).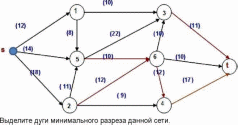




Дуги минимального разреза: (1, 3), (5, 3), (4, t), (3, t), (6, t).

Луги минимального разреза: (1 3) (5 3) (5 6) (2 6) (2 4)

Выберите все верные ответы (может быть несколько или один). Определите сложность булевой функции. Число вхождений аргументов в функцию обозначьте символом S. /(®1, Ж2, Жз) = Х\Х2 Жз V ЖГЖ2ЖЗ V Ж1Ж2 Ж3 V Ж1Ж2Ж3 S = 4 5 = 12 S = 6 S = 3 Неверно Выберите все верные ответы (может быть несколько или один). Запишите в форме СДНФ функцию f(x\, Ж2, Ж3), представленную таблицей истинности. *1

Х2

СО н

/(Ж1, ж2, ж3)

0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

/(ж 1, Ж2, Жз) = Ж1Ж2Ж3 V Ж1Ж2Ж3 V Ж1Ж2"Жз

/(ж 1, ж₂, ж₃) = жГж₂ж₃ V Ж1Ж2Ж3 V x^x^xi

/(ж 1, Ж2, Жз) = Ж1 Ж2 Жз V Ж1Ж2Ж3 V Ж1Ж2"Жз V Ж1Ж2Ж3

Верно




Выберите все верные ответы (может быть несколько или один).

Постройте скелет графа где

С/= {(Ж1Ж₂ ), (Ж1Ж1 ), (ж₂ж₂), (ж₃ж₂ ), (ж₂ж₃), (Ж1Ж₃ ), (Ж1Ж₄ ), (ж₄ж₂ ), (ж₃ж₃), (ж₄ж₃), (ж₃ж₄), (ж₄ж₄) Ответ запишите в виде последовательности рёбер множества U.