КР. Контрольная работа 1 по дисциплине Методы принятия управленческих решений Вариант 26, 12 Содержание

• Название: Контрольная работа 1 по дисциплине Методы принятия управленческих решений Вариант 26, 12 Содержание
• Дата: 05.12.2021
• Размер: 1.53 Mb.
• Имя файла: КР.doc
• Тип: Контрольная работа; #292340
• страница: 3 из 4

Двойственная задача:

Целевая функция:

Ограничения:





Основные переменные: , , ,

Дополнительные переменные: ,

Значение целевой функции:

Объективно обусловленная оценка y₁=0 и y₂=0 – равны нулю, это указывает на то, что у нас избыток цветных металлов и стали, и это свидетельствует о их недефицитности. Y₃=0,333 и y₄=0,833, т.е. больше нуля, это говорит о том, что ресурсы (токарные и фрезерные работы) полностью используются в оптимальном плане, являются дефицитными, т.е. сдерживающими рост целевой функции.

Правые части этих ограничений равны левым частям:









Ресурсы – цветные металлы и сталь используются не полностью: цветные металлы (9150<12600), сталь(10300<12000), поэтому имеют нулевую двойственную оценку (y₁=0 и y₂=0):









Эти ресурсы не влияют на план выпуска продукции.

2.2. Задание по теме 3. Вероятностно-статистические методы принятия решений.

В течение одиннадцати последовательных месяцев фиксировался объём продаж одного изделия фирмы Y(t)(тыс. штук). Временной ряд Y(t)этого показателя приведен ниже.

Номер		Номер наблюдения (t= 1, 2, …, 11)
варианта	1		2	3	4	5	6	7		8	9	10	11
12	51		53	52	54	57	60	62		64	66	65	68

Требуется:

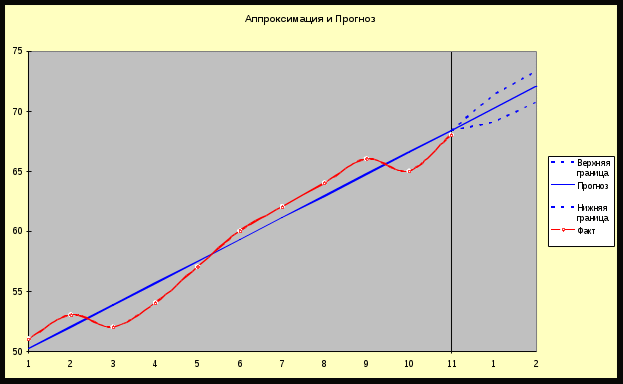
1) построить график временного ряда, сделать вывод о наличии тренда;

2) построить линейную модель Y(t)=a_о+а₁t,параметры кото­рой оценить с помощью метода наименьших квадратов (МНК);

3) оценить адекватность построенной модели, используя свой­ства остаточной компоненты e(t);

4) оценить точность модели на основе использования средней относительной ошибки аппроксимации;

5) по построенной модели осуществить прогноз спроса на следу­ющие два месяца (доверительный интервал прогноза рассчитать при доверительной вероятности P = 75%).

Модели временного ряда - Показатель-B
Таблица кривых роста
Функция	Критерий	Эластич ность
Y(t)=+48.364+1.818*t	1,616	0,184
Y(t)=+48.243+1.874*t -0.005*t*t	1,816	0,184
Y(t)= +49.013*exp(+0.031*t)	1,730	0,185
Y(t)= +47.227+7.571*ln(t)	6,665	0,125
Y(t)= (+48.474)*(+1.037)**t*(+1.000)**(t*t)	1,798	0,185
Y(t)= +50.045+2.188*t-1.664*sqr(t)	1,775	0,188
Y(t)= t/(+0.013+0.014*t)	28,721	0,135
Выбрана функция Y(t)=+48.364+1.818*t
Характеристики базы моделей
Модель	Адекват ность	Точность	Качество
Y(t)=+48.364+1.818*t	50,396	84,914	76,284
Лучшая модель Y(t)=+48.364+1.818*t
Параметры моделей
Модель	a1	a2
Y(t)=+48.364+1.818*t	48,364	1,818
Таблица остатков
номер	Факт	Расчет	Ошибка абс.	Ошибка относит.
1	51,000	50,182	0,818	1,604
2	53,000	52,000	1,000	1,887
3	52,000	53,818	-1,818	-3,497
4	54,000	55,636	-1,636	-3,030
5	57,000	57,455	-0,455	-0,797
6	60,000	59,273	0,727	1,212
7	62,000	61,091	0,909	1,466
8	64,000	62,909	1,091	1,705
9	66,000	64,727	1,273	1,928
10	65,000	66,545	-1,545	-2,378
11	68,000	68,364	-0,364	-0,535
Характеристики остатков
Характеристика	Значение
Среднее значение	0,000
Дисперсия	1,322
Приведенная дисперсия	1,616
Средний модуль остатков	1,058
Относительная ошибка	1,822
Критерий Дарбина-Уотсона	1,391
Коэффициент детерминации	1,000
F - значение ( n1 = 1, n2 = 9)	24137,100
Критерий адекватности	50,396
Критерий точности	84,914
Критерий качества	76,284
Уравнение значимо с вероятностью 0.95
Таблица прогнозов (p = 80%)
Упреждение	Прогноз	Нижняя граница	Верхняя граница
1	70,182	69,042	71,321
2	72,000	70,709	73,291

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R		0,98
R-квадрат		0,96
Нормированный R-квадрат		0,96
Стандартная ошибка		1,27
Наблюдения		11,00
Дисперсионный анализ
			df	SS	MS	F	Значимость F
Регрессия			1,00	363,64	363,64	225,00	0,00
Остаток			9,00	14,55	1,62
Итого			10,00	378,18
			Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение			48,36	0,82	58,83	0,00	46,50	50,22	46,50	50,22
t			1,82	0,12	15,00	0,00	1,54	2,09	1,54	2,09
ВЫВОД ОСТАТКА
Наблюдение			Предсказанное Y	Остатки
1,00			50,18	0,82
2,00			52,00	1,00
3,00			53,82	-1,82
4,00			55,64	-1,64
5,00			57,45	-0,45
6,00			59,27	0,73
7,00			61,09	0,91
8,00			62,91	1,09
9,00			64,73	1,27
10,00			66,55	-1,55
11,00			68,36	-0,36