КР. Контрольная работа 1 по дисциплине Методы принятия управленческих решений Вариант 26, 12 Содержание
 Скачать 1.53 Mb.
|
2.3. Задание по теме 4. Управленческие решения в задачах логистики и массового обслуживания.Вариант 12. В прачечной самообслуживания установлены четыре стиральные машины. По статистике, в прачечную в течение часа заходят в среднем три клиента. Если клиент приходит в тот момент, когда все стиральные машины заняты, то он уходит, не дожидаясь обслуживания, поскольку стирка занимает два часа. Вычислить основные характеристики работы прачечной как СМО с отказами. Предложите управленческое решение для оптимизации работы прачечной. Решение: Интенсивность потока обслуживания: 1. Интенсивность нагрузки. ρ = λ • tобс = 3 • 2 = 6 Интенсивность нагрузки ρ=6 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 0.87% в течение часа канал будет не занят, время простоя равно tпр = 0.5 мин. Вероятность того, что обслуживанием: занят 1 канал: p1 = ρ1/1! p0 = 61/1! • 0.0087 = 0.0522 заняты 2 канала: p2 = ρ2/2! p0 = 62/2! • 0.0087 = 0.16 заняты 3 канала: p3 = ρ3/3! p0 = 63/3! • 0.0087 = 0.31 заняты 4 канала: p4 = ρ4/4! p0 = 64/4! • 0.0087 = 0.47 3. Доля заявок, получивших отказ. Значит, 47% из числа поступивших заявок не принимаются к обслуживанию. 4. Вероятность обслуживания поступающих заявок. В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: pотк + pобс = 1 Относительная пропускная способность: Q = pобс. pобс = 1 - pотк = 1 - 0.47 = 0.53 Следовательно, 53% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 5. Среднее число каналов, занятых обслуживанием. nз = ρ • pобс = 6 • 0.53 = 3.18 канала. 6. Среднее число простаивающих каналов. nпр = n - nз = 4 - 3.18 = 0.8 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 80% занята обслуживанием. 8. Абсолютная пропускная способность. A = pобс • λ = 0.53 • 3 = 1.59 заявок/час. 9. Среднее время простоя СМО. tпр = pотк • tобс = 0.47 • 2 = 0.94 час. 10. Среднее число обслуживаемых заявок. Lобс = ρ • Q = 6 • 0.53 = 3.18 ед. Число заявок, получивших отказ в течение часа: λ • p1 = 1.41 заявок в час. Номинальная производительность СМО: 4 / 2 = 2 заявок в час. Фактическая производительность СМО: 1.59 / 2 = 80% от номинальной производительности. 2.4. Задание по теме 5. Метод экспертных оценок.Вариант 12. Десять экспертов оценили прогноз качества поршневых насосов
Методом статистической обработки результатов экспертных оценок найти точечный и интервальные прогнозы качества (в баллах). Решение: Расположив результаты оценок в порядке возрастания, получу следующий ряд:
Нахожу медиану. В общем виде при наличии n значений медиана отвечает  - му порядковому номеру.В последовательности из 10 данных значений медиана будет отвечать  - му порядковому номеру (т.е. номеру, который находится посередине между 5-м и 6-м значениями). Таким образом, медиана равна  Определю значение первого и третьего квартиля: Нижний (первый) квартиль Q1 = 3,7+0,75*(4,4-3,7) = 4,225; Верхний (третий) квартиль Q3 = 5,3+0,25*(5,9-5,3) = 5,45.
В качестве точечной оценки принимаю среднее значение прогнозируемой величины: 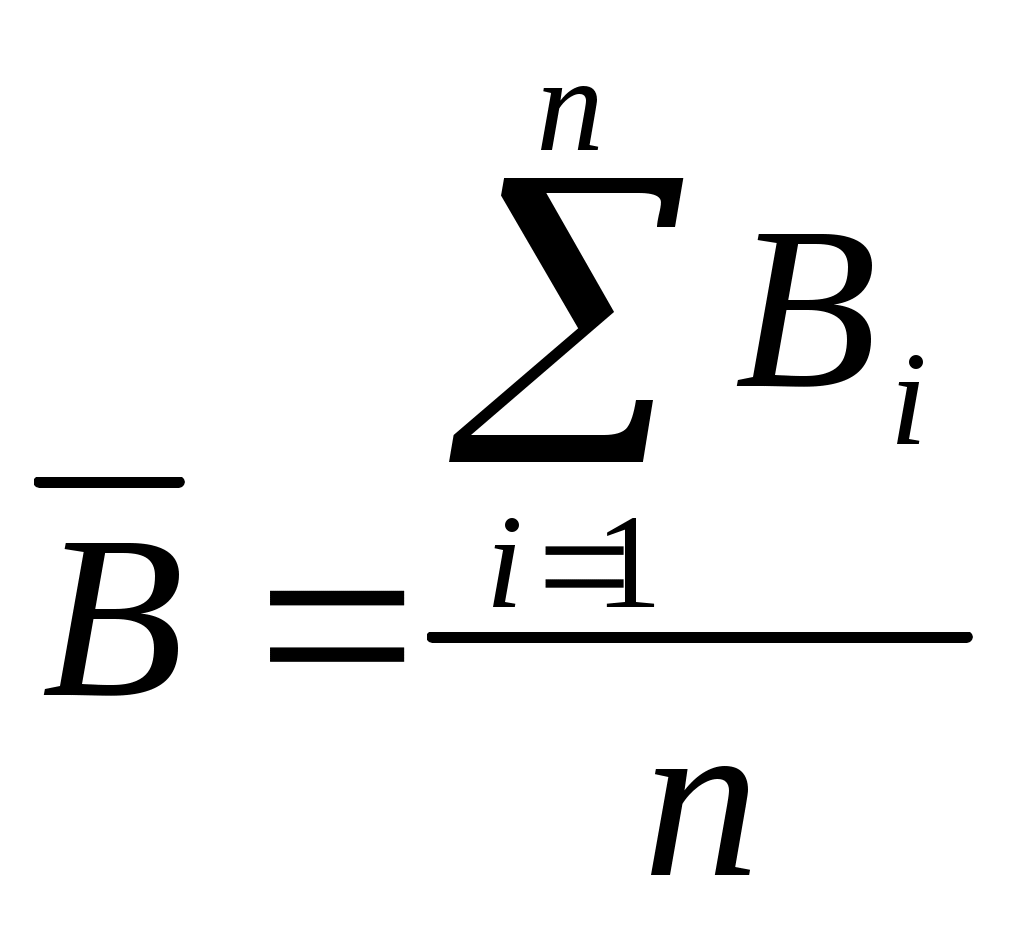  Для нахождения дисперсии D и оценки j для доверительного интервала используются графы 3 и 4 таб. 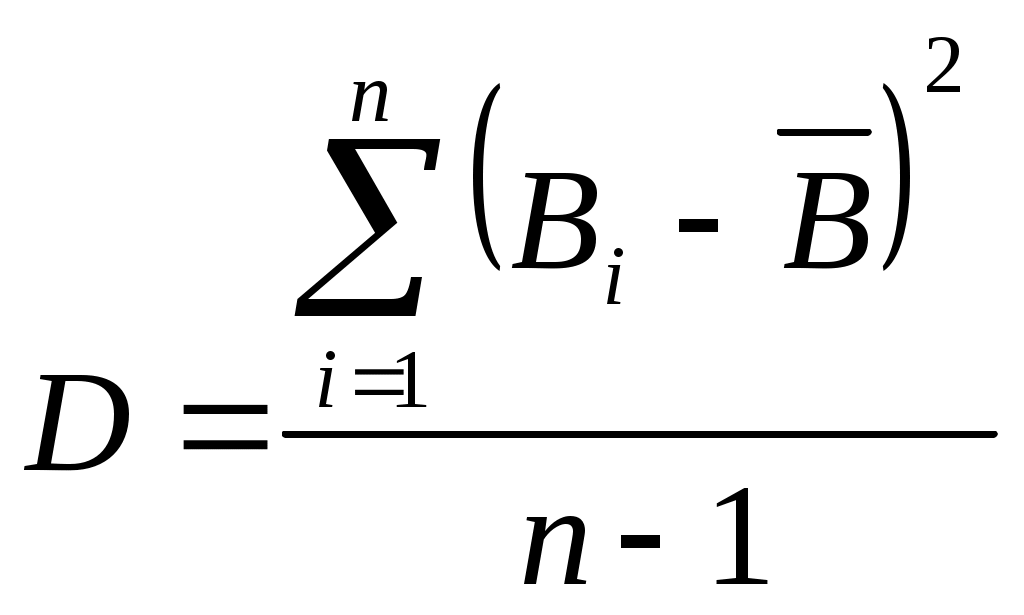    Верхняя граница доверительного интервала  нижняя граница  Список литературы Гармаш А.Н., Орлова И.В. Математические методы в управлении: Учебное пособие. – М.: Вузовский учебник: ИНФРА-М, 2012. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учебное пособие. – 3-е изд., перераб. и доп. – М.: Вузовский учебник: ИНФРА-М, 2012. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач – 2-е изд., испр. и доп. М.: Вузовский учебник: ИНФРА-М, 2012. http://edu.nstu.ru/courses/simulation_system/part32.htm#text24 |
