максим. Контрольная работа 1 по дисциплине Строительная механика наименование дисциплины в соответствии с учебным планом

• Название: Контрольная работа 1 по дисциплине Строительная механика наименование дисциплины в соответствии с учебным планом
• Дата: 30.05.2022
• Размер: 2.22 Mb.
• Имя файла: максим.docx
• Тип: Контрольная работа; #558127

СМК Ф 7.5.0-01-02

МИНОБРНАУКИ РОССИИ

федеральное государственное бюджетное

образовательное учреждение высшего образования

«Череповецкий государственный университет»

Инженерно-технический институт

наименование института (факультета)

строительства

наименование кафедры

Контрольная работа № 1

по дисциплине Строительная механика

наименование дисциплины в соответствии с учебным планом

студента (студентки) Палагин Евгений Сергеевич

фамилия, имя, отчество

Специальность 0.8.03.01

Группа 3СТб-01-1зп-19

Вариант №

121

Шифр зачетной книжки

190803010121

Проверил	Медведева Н.В.
	ФИО преподавателя

Оценка	…………………
Количество баллов
Подпись		………………

Дата ______________

Тема
1. Задание

Для многопролетной шарнирно-консольной балкитребуется:

1) вычертить схему балки и указать на ней все размеры и нагрузки в соответствии с заданием (рис. 1,а);

2) провести анализ статической определимости и геометрической неизменяемости системы;

3) построить эпюры M и Q (аналитически);

4) построить линии влияния опорных реакций (по выбору студента), а также линии влиянияM и Q в сечении (по заданию);

5) определить по линиям влияния значения опорных реакций, изгибающих моментов и поперечных сил от заданной нагрузки;

6) определить прогиб и угол поворота сечения (по заданию).
2. Проверка статической определимости и геометрической неизменяемости системы

2.1. Для обеспечения статической определимости многопролётной шарнирно-консольной балки число шарниров Ш, введённых в пролёты, должно удовлетворять условию
Ш = С_оп – 3, (1)

где С_оп – число опорных стержней; 3 – число уравнений статики для плоской системы произвольно расположенных сил.

В рассматриваемом варианте имеем: Ш = 2 (в точках В и D), С_оп = 5 (три в точке А и по одному в точках С и Е); тогда Ш = 5 – 3 = 2. Следовательно, условие (1) выполняется, система статически определима и может быть геометрически неизменяемой.

2.2. Для доказательства геометрической неизменяемости системы выполним анализ её геометрической структуры.

Исходные данные: а=2 м, M₁=5 кНм, M₂=0 кНм, q₁=0 кН/м, q₂=5 кН/м, F₁=0 кН, F₂=4 кН, схема №1, сечение – m, перемещение - ∆_m (Поменять на ваши)

Исходная схема с заданными нагрузками и размерами:

(перерисовать исходную схему №7 с заданными нагрузкими)



Заданная многопролетная балка образована из трех простых балок:

а) Балка АB с тремя опорными стержнями, которые не параллельны и не пересекаются в одной точке.

б) Балка BСD присоединена к балке АС шарниром B и к “земле” стержнем C, осевая линия которого не проходит через шарнир С.

в) Балка DE присоединена к геометрически неизменяемой системе шарниром D и опорным стержнем E, осевая линия которого не проходит через шарнир Е.

Следовательно, система геометрически неизменяема.

Построение эпюр M и Q

2.2.1. Первой рассчитываем самую «верхнюю» балку DE.

1. 
   Начинаем с определения реакций опор, используя три уравнения статики для плоской системы: ∑М_D = 0; ∑М_E = 0; ∑F_Y = 0.
   

∑М_E=–8,8∙R_D+q₁∙4,4∙4,4/2–M₂=0; R_D=23,4/8,8=2,66 кН;

∑М_D = 8,8∙R_E+q₁∙4,4∙13,2/2–M₂=0; R_E=170,2/8,8=19,34 кН.

Проверяем условие:

∑F_Y= R_E+R_D–q₁∙4,4=2,66+19,34–22=0 (верно).

2. 
   Строим для данной балки DE эпюры поперечных сил и изгибающих моментов
   

Участок 1: 0≤x₁≤4,4

Q= R_D; М= R_D∙x₁;

При х₁=0: Q=2,66 кН, M=0 кНм

При х₁=4,4: Q=2,66 кН, M= 11,7 кНм

Участок 2: 4,4≤x₂≤6,6

Q= R_D–q₁∙(x₂–4,4); М= R_D∙x₂–q₁∙(x₂–4,4)²/2;

При х₂=4,4: Q= 2,66 кН, M= 11,7 кНм

При х₂=6,6: Q=–8,34; кН, M= 5,45 кНм

Экстремум на эпюре М: Q₀ = dM /dх = R_D – q₂∙(x₄-4,4)=0  x₄=4,93 м.

M_max=14,41 кНм

Участок 3: 6,6≤x₃≤8,8

Q= R_D–q₁∙(х₃–4,4); М= R_D∙x₃–q₁∙(х₃–4,2)²/2 + M₂;

При х₃=4: Q= –8,34 кН, M= 30,45 кНм

При х₃=6: Q=–19,34 кН, M=0 кНм

2.2.2. Переходим к балке ВС

К нагрузке F₁, действующей на балку, добавим R^_D = 2,66 кН – силу взаимодействия с вышележащей балкой DE.

1. 
   Начинаем с определения реакций опор, используя три уравнения статики для плоской системы: ∑М_B = 0; ∑М_C = 0; ∑F_Y = 0.
   

∑М_C= –R_B∙4,4+F₁∙2,2–R^_D∙2,2=0; R_B=2,98/4,4= 0,67 кН.

∑М_B= R_C∙4,4 – F₁∙2,2 – R^_D∙6,6=0; R_С=26,36/4,4= 5,99 кН.

Проверяем условие:

∑F_Y= R_С + R_B – F₁–R^_D = 0,67+5,99–4–2,66 = 0 (верно).

2. 
   Строим для балки ВС эпюры поперечных сил и изгибающих моментов
   

Участок 1: 0≤x₄≤2,2

Q= R_В; М= R_В∙x₄;

При х₄=0: Q=0,67 кН, M=0 кНм

При х₄=2,2: Q=0,67 кН, M=1,47 кНм

Участок 2: 2,2≤x₅≤4,4

Q= R_В– F₁; М= R_В∙x₅– F₁(x₅– 2,2);

При х₅=2,2: Q= –3,33 кН, M= 1,47 кНм

При х₅=4,4: Q= –3,33 кН, M= –5,85 кНм

Участок 3: 4,4≤x₆≤6,6

Q= R_С+ R_В–F₁; М= R_B∙x₆+ R_C∙(х₆–4,4) –F₁∙(х₆–2,2);

При х₆=4,4: Q=2,66 кН, M= –5,85 кНм

При х₆=6,6: Q=2,66 кН, M=0 кНм

2.2.3. Строим для балки АВ эпюры поперечных сил и изгибающих моментов

На балку АВ действует сила R^_В=0,67 кН от вышележащей балки СD.

1. 
   Начинаем с определения реакций опор, используя три уравнения статики для плоской системы: ∑М_А = 0; ∑М_В = 0; ∑F_Y = 0.
   

∑М_А= – R^_В∙4,4 – М_А=0; М_А=–2,95 кН;

∑F_Y= R_А–R^_B=0; R_А=0,67 кН.

Проверяем условие:

∑М_В= – М_А – R_А∙4,4+ R^_B ∙0=2,95–0,67∙4,4=0 (верно).

3. 
   Строим для балки АВ эпюры поперечных сил и изгибающих моментов
   

Участок 1: 0≤x₇≤4,4

Q= R_А; М= М_А+R_А∙x₇;

При х₇=0: Q= 0,67 кН, M=–2,95 кНм

При х₇=4,4: Q= 0,67 кН, M=0 кНм

2.3. Построение окончательных эпюр внутренних усилий и их проверка

Выполним статическую проверку для всей многопролетной балки (сумма заданных сил и реакций опор должна быть равна нулю):

∑F_Y= R_А+R_C+R_E–F₁–q₁∙4,4=0,67+5,99+19,34-4-5∙4,4=0 (верно)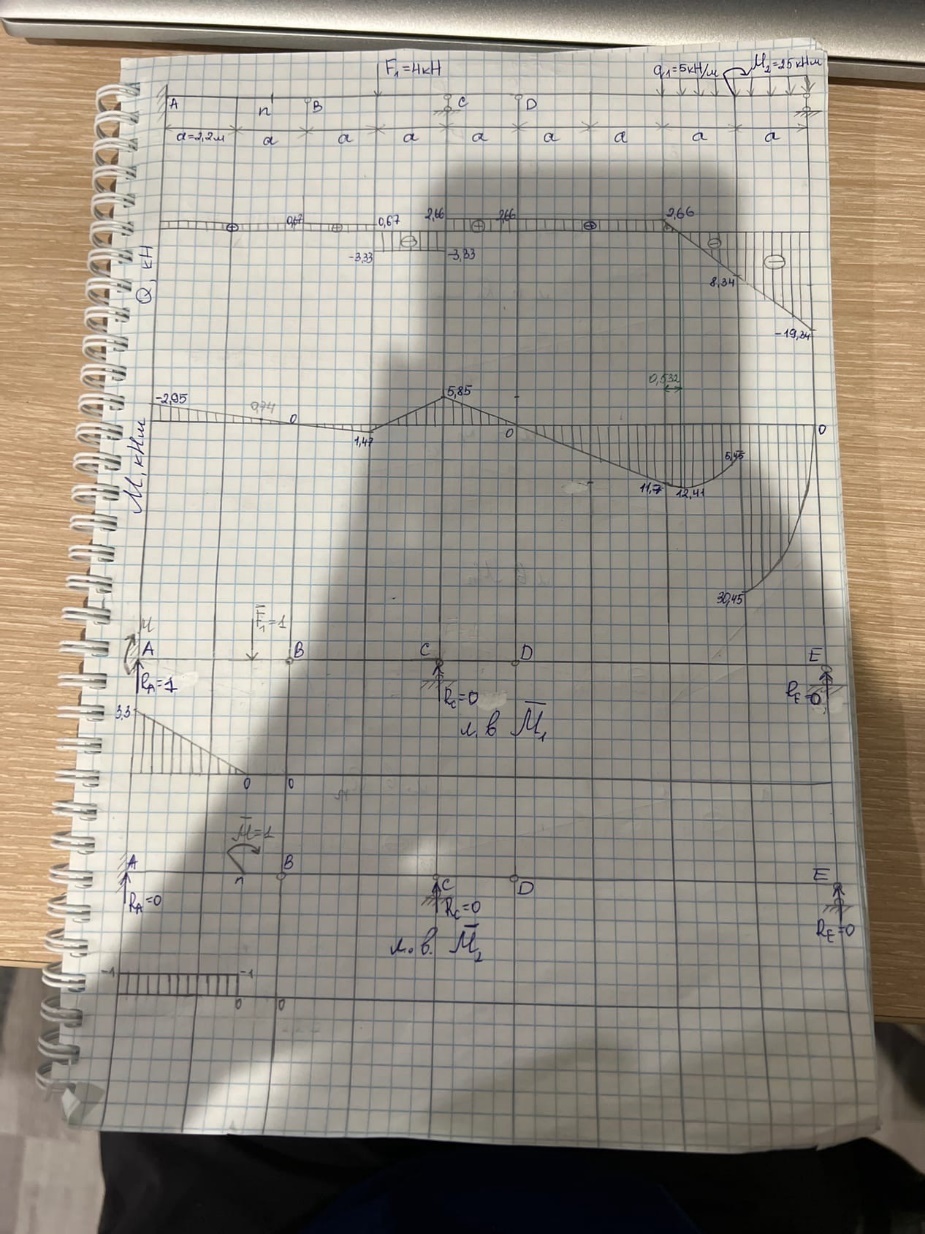



Это половина вот этой фотки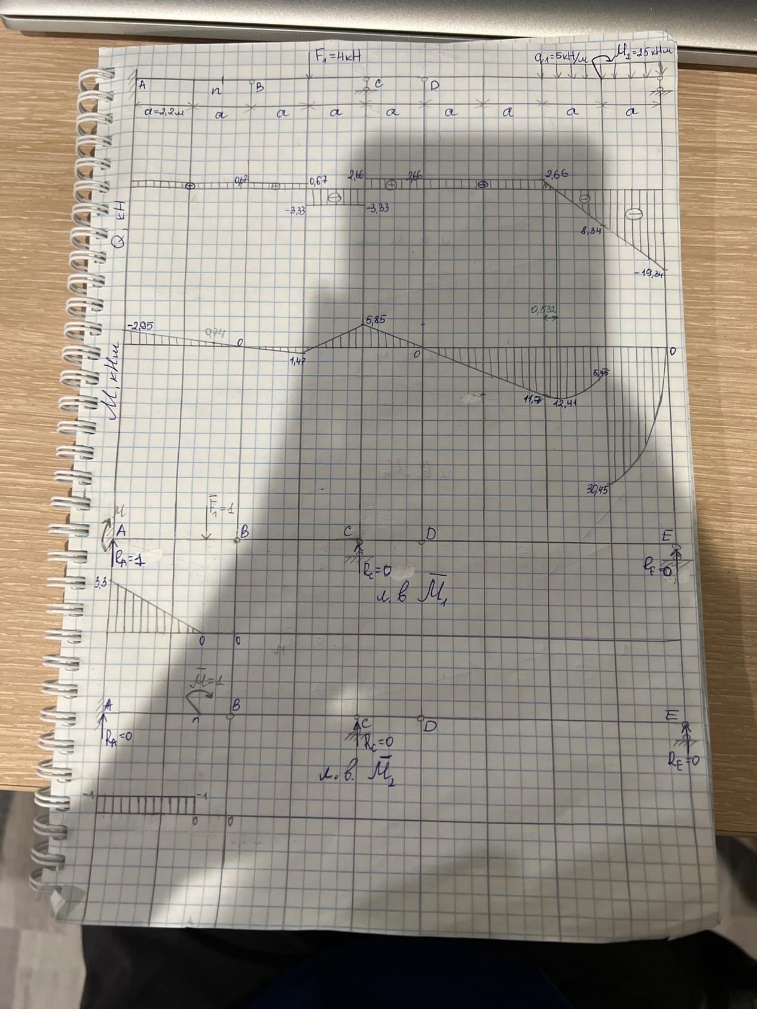

2.4. Построение ЛВ опорных реакций

1. 
   Линия влияния опорной реакции R_А.
   

Построение начинаем с балки АВ, которой принадлежит рассматриваемая опора А. Груз F 1 движется по балке АВ с жестким закреплением. Тогда участок AВ линии влияния R_A имеет тот же вид, что и линия влияния реакции R_A отдельно стоящей простой балки. При положении груза F 1 в точке А имеем: R_А = 1

При движении груза F 1 по балке BCD на балку АВ в точке D передается усилие R^_В. Так как значение опорной реакции R_B при движении груза F 1 по балке BСD меняется по линейному закону, то и реакция R_А при этом будет меняться по закону прямой, соединяющей узловые ординаты (рис. 5, д):

– при положении груза F 1 в точке B: R_A = 1;

– при положении груза F 1 в точке D: R_A = – 0.5.

При движении груза F 1 по балке DЕ на балку BСD, а следовательно, и на балку АВ передается в точке D усилие R^_D. Так как значение опорной реакции R_D при движении груза F 1 по балке DE меняется по линейному закону, то и реакция R_А при этом будет меняться по закону прямой, соединяющей узловые ординаты:

– при положении груза F 1 в точке D: R_A = –0.5;

– при положении груза F 1 в точке E: R_A = 0.

1. 
   Линия влияния опорной реакции R_C.
   

Рассмотрим вначале движение груза F 1 по балке BCD, которой принадлежит опора C. При положении груза F 1 в точке D значение R_C = (4+2)/4 = 1,5.

При движении груза F 1 по балке DE на балку BCD в точке D передается усилие R^_D. Поскольку значение реакции R_E от единичной силы, приложенной в точке D, составляет 1,5, то реакция от силы R^_D будет равна R_E=1,5R_D.

Значение R_D как опорной реакции изменяется по линейному закону. Следовательно, и R_С при движении груза F 1 по балке BСD меняется по закону прямой, соединяющей узловые ординаты:

– при положении груза F 1 в точке B: R_C = 0;

– при положении груза F 1 в точке D: R_C = 1,5.

При движении груза F 1 по основной балке АВ усилие на вышележащую балку BСD не передается. При движении груза по участку АВ все усилия в балке BCD равны нулю и R_C = 0. Соответствующий участок АВ линии влияния совпадает с осью абсцисс.

2.5. Построение ЛВ внутренних усилий в сечении n балки:

Вначале рассмотрим передвижение груза F 1 по балке AB, которой принадлежит сечение n. Сечение n находится в пролёте AB, следовательно, при построении используем линии влияния для балки с жестким закреплением: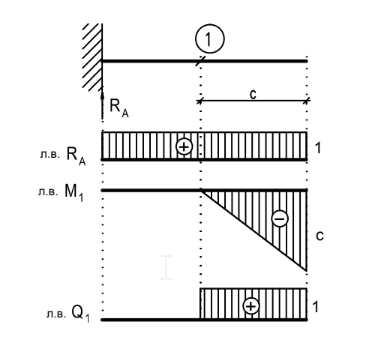



При движении F 1 по вспомогательной балке BCD усилие R_C, передаваемое на балку ABC, меняется по линейному закону, изгибающий момент M_n линейно изменяется от –1,1 (сила F 1 в точке В) до 0,55 (сила F 1 в точке D), что и отражает участок ВD линии влияния M_n.

При движении F 1 по вспомогательной балке DE усилие R_D, передаваемое на балку ABC, меняется по линейному закону, изгибающий момент M_n линейно изменяется от 0,55 (сила F 1 в точке В) до 0(сила F 1 в точке D), что и отражает участок DE линии влияния M_n.

2. Линия влияния поперечной силы Q_n в сечении n.

Аналогично, строим линию влияния Q_n.

Результат:


2.6. Определение усилий от заданной нагрузки по линиям влияния

1. 
   Опорная реакция R_A. Вычисляем:
   

– площадь участка линии влияния R_А, находящегося под распределенной нагрузкой ω₁= –(0,254,4/2)= –0,55м²;

– ордината линии влияния под силой F₁: y₁  0,5;

– тангенс угла наклона участка линии влияния R_A в точке приложения сосредоточенного момента: tg φ₁ = 0,25/8,8= 0,057;

Тогда, согласно формуле, имеем:

R_А  F₁  0,5 – q  0,55 + M  0,057  4  0,5 – 50,55+25 0,057  0,67 кН, что соответствует результату расчёта, приведённого в п. 2.2.1.

2. 
   Опорная реакция R_C.
   

Вычисляем:

– площадь участка линии влияния R_С, находящегося под распределенной нагрузкой: ω₁=0,754,4/2=1,65м²;

– тангенс угла наклона участка линии влияния R_С в точке приложения сосредоточенного момента: tg φ₂ = –1,5/8,8 = –0,17;

– ордината линии влияния под силой F₁: y₁  0,5;

Тогда, согласно формуле, имеем:

R_C  М  (–0,17) + q 1,65 + F₁0,5 2 + 8,25 – 4,26 = 5,99 кН, что соответствует результату расчёта, приведённого в п. 2.2.1 данного пособия.

2.6.2 Определяем внутренние усилия

1. 
   Изгибающий момент М_n.
   

– Площадь участка линии влияния М_n, находящегося под распределенной нагрузкой: ω=0,2754,4/2=0,605м² .

– Ордината линии влияния под силой F₁: y₁  –0,55.

– тангенс угла наклона участка линии влияния М_n в точке приложения сосредоточенного момента: tg φ = –0,55/8,8= –0,0625;

Согласно формуле получаем: M_n=0,605 q – F₁0,55 + М  (–0,0625)=0,74 кНм, что соответствует результату аналитического расчёта.

б) Поперечная сила Q_n в сечении n.

Площади участков линии влияния Q_n под распределённой нагрузкой равны: ω₁= –0,254,4/2= –0,55

– Ордината линии влияния под силой F₁: y₁  0,5.

– тангенс угла наклона участка линии влияния Q_n в точке приложения сосредоточенного момента: tg φ = 0,5/8,8= 0,057;

Подставляя в формулу указанные выше значения, получаем:

Q_n= М  0,057 + q (–0,55) + F₁0,5 = 0,675 кН, что соответствует результату аналитического расчёта.

2.6.3. Сравним результаты, полученные по линиям влияния, со значениями, найденными при построении эпюр (см. табл. 2). Расхождения результатов расчётов не превышают 0,17 %. Допускаются расхождения не более 0,5–1 %.

Наименование усилия	Значение, полученное по линиям влияния	Значение, полученное при построении эпюр	Расхождение, %
RA	0,67 кН	0,67 кН	0
RC	5,99 кН	5,99 кН	0
Mn	0,74 кНм	0,74 кНм	0
Qn	0,675 кН	0,67 кН	0,8

2.7. Определение прогиба _n и угла поворота _n сечения n.

2.7.1 Рассмотрим определение вертикального перемещения (прогиба) сечения n.

1. 
   Строим единичную эпюру без использования «поэтажной» схемы
   

Для определения опорных реакций помимо уравнений статики составляем дополнительные уравнения, выражающие равенство нулю изгибающего момента в шарнирах.

∑М_D^прав= 8,8R_Е=0; R_Е=0;

∑М_В^прав= 4.4R_С +15,4R_Е =0; R_С=0

∑М_D^лев= 2,2R_С+7,7F11R_AM=0; M=2,2R_С-7,7F+11R_A;

∑М_В^лев= 1,1F4,4R_AM=0;

Подставляя M во второе уравнение получаем:

6,66,6R_A=0;R_А=1

M=0-7,7+11=3,3

Для проверки составляем уравнение:

∑F_Y= R_АF= 11=0(верно).

Следовательно, реакции опор определены верно.

2. 
   Для построения единичной эпюры изгибающих моментов вычисляем значения изгибающих моментов в сечениях, соответствующих точкам приложения сосредоточенных активных и реактивных сил:
   

M_A =3,3 ;

M_n= R_A·3,3  M_A =3,33,3=0

При построении эпюр учитываем, что изгибающие моменты в шарнирах B и D равны нулю.

2.7.3. Для определения угла поворота сечения n выбираем новое единичное состояние – снимаем с балки нагрузку и прикладываем единичный момент M₂ 1. Строим единичную эпюру M₂, предварительно вычисляя реакции опор с использованием «поэтажной» схемы балки.

Первой рассчитываем балку DE.

Внешние нагрузки представлены только сосредоточенными силами, приложенными к опорным точкам D и E. Такое нагружение не вызывает никаких внутренних силовых факторов, а только реакции опор.

Рассчитываем балку BCD.

Внешние нагрузки представлены только сосредоточенными силами, приложенными к опорным точкам B и C. Такое нагружение не вызывает никаких внутренних силовых факторов, а только реакции опор.

Рассчитываем балку AB.

∑M_A = –M_A –M₁ = –M_A – 1 = 0 ⇒M_A = –1 кНм

∑Y = R_A = 0 ⇒ R_A = 0

Для проверки вычислим сумму моментов всех сил относительно точки B:

∑M_B = –M_A – 4,4R_A –M₁ = 1 + 0·4.4–1 =1 + 0 – 1 = 0 (верно)

Участок 1 (0 ≤ х₁ ≤ 3.3):

Q= R_A ; М= R_A ∙x₄+М₁;

При х₁=0: Q=0 кН, M= –1 кНм

При х₁=2: Q=0 кН, M= –1 кНм

Участок 2 (3.3 ≤ х₂ ≤ 4.4):

Q= R_A ; М= R_A ∙x₄+М₁+М_А;

При х₂=0: Q=0 кН, M= 0 кНм

При х₂=2: Q=0 кН, M= 0 кНм

Построение окончательных эпюр внутренних усилий и их проверка

Выполним статическую проверку для всей многопролетной балки (сумма заданных сил и реакций опор должна быть равна нулю):

∑F_Y= R_А+R_С+R_Е=0 (верно)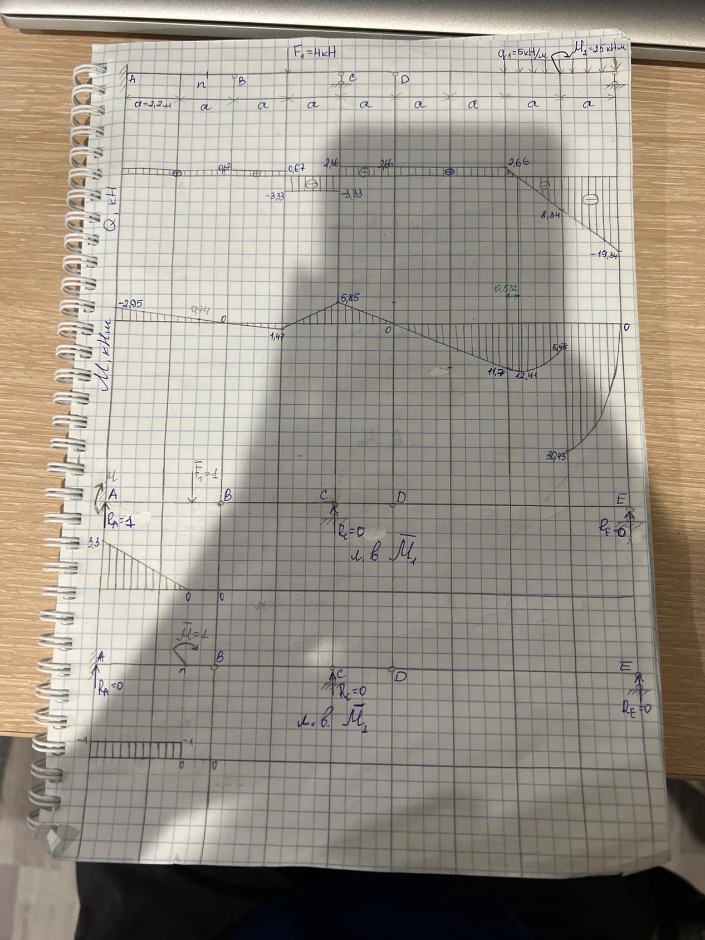



2.8. Изображение характера изогнутой оси балки

Построение изображения изогнутой оси балки



СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. 
   А.В. Дарков, Н.Н. Шапошников Строительная механика. - М.: Высшая школа, 1986. - 607 с.
   
2. 
   Н.А. Бачурина, Т.С. Камыгина СТРОИТЕЛЬНАЯ МЕХАНИКА. Расчет многопролетной статически определимой балки. Методические рекомендации. Учебно-методическое пособие . - г. Череповец: 2015. - 49 с.