Главная страница
Навигация по странице:

  • Межрегиональный учебный центр переподготовки специалистов Контрольная работа № 1

  • Выполнил

  • Ответ

    		•

    Контрольная работа 1. Контрольная работа №1. Контрольная работа 1 по дисциплине Теория вероятностей и математическая статистика Выполнил Федоров Александр Валерьевич


    Скачать 24.84 Kb.
    НазваниеКонтрольная работа 1 по дисциплине Теория вероятностей и математическая статистика Выполнил Федоров Александр Валерьевич
    АнкорКонтрольная работа 1
    Дата11.07.2022
    Размер24.84 Kb.
    Формат файлаdocx
    Имя файлаКонтрольная работа №1.docx
    ТипКонтрольная работа
    #628618

    Министерство цифрового развития, связи и
    массовых коммуникаций Российской Федерации

    Сибирский государственный университет телекоммуникаций и информатики

    (СибГУТИ)
    Межрегиональный учебный центр переподготовки специалистов


    Контрольная работа №1

    по дисциплине: Теория вероятностей и математическая статистика


    Выполнил: Федоров Александр Валерьевич

    Группа: ПБТ-11

    Семестр: 3

    Вариант: 5

    Проверил: Храмова Татьяна Викторовна

    Новосибирск, 2022

    Задание 1

    Сколько 5-ти буквенных слов можно составить из букв слова

    Х О Д О Р?

    Решение. Переставить буквы в слове можно5! способами (формула числа перестановок из n элементов: 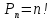). При этом в слове одна одинаковая буква О – две буквы.


    Всего 5!, “копий” из за буквы О-2!

    Ответ: 60.
    Задание 2

    Цель, по которой ведётся стрельба, может находится на первом участке с вероятностью 0,4, на втором участке с вероятностью 0,6. Цель, находящуюся на первом участке, поражают с вероятностью 0,8, на втором – с вероятностью 0,6. Найти вероятность поражения цели.

    Решение.

    А – событие цель поражена

    B – событие цель не поражена

    - Вероятность нахождения цели на первом участке

    - Вероятность нахождения цели на втором участке
    Согласно статистическому определению вероятности P ( ) = 0.4, P ( ) = 0.6. Вероятность события А известны P ( )=0.8, P (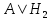 )=0.6.
    Вычисляем по формуле полной вероятности:

    P(A) = P( )P(A| ) + P( )P(A| ) = 0.4×0.8+0.6×0.6 = 0.32+0.36 = 0.68

    Ответ: 0.68

    Задание 3

    Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной рядом распределения.


    ξ
    -3
    -1
    1
    3

    p
    0,1
    0,1
    0,7
    0,1


    Решение: запишем формулу для вычисления математического ожидания и подставим в неё данные задачи:


    Запишем формулу для вычисления дисперсии и подставим в неё данные задачи: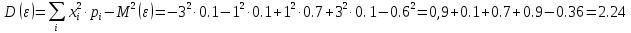



    Среднее квадратическое отклонение вычисляется по формуле: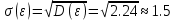

    Ответ: , , .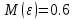
    Задание 4

    Случайная величина распределена по нормальным закону с параметрами, а, б. Найдите вероятность того, что случайная величина принимает значения из интервала [к1; к2]

    a = 10, σ = 3, k1 = 7, k2 = 13
    Решение: Вероятность попадания нормально распределённой величины в интервал вычисляется по формуле

    Согласно условиям задачи, имеем: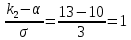



    По таблице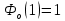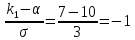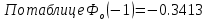



    В результате:

    Ответ: 0.6826

    написать администратору сайта