Лабораторная работа 2 по теории вероятности. Лабораторная работа 2 Задание 1
 Скачать 128.47 Kb. Скачать 128.47 Kb.
|
|
Лабораторная работа №2 Задание 1. Получить с использованием Пакета анализа выборку объема n=40 из генеральной совокупности, в которой ζ распределена по нормальному закону с параметрами m=4 и σ=0,5. Найти точечные оценки математического ожидания, дисперсии, стандартного отклонения, а также стандартную ошибку математического ожидания: а) по данным малой выборки (n=20); б) по данным большой выборки (n=40); Задание 2. 2.1. Найти доверительные интервалы, соответствующие доверительные вероятности 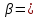 0,95, для оценок математического ожидания, полученных в задании 1.2, без использования MS Excel. 0,95, для оценок математического ожидания, полученных в задании 1.2, без использования MS Excel.2.2. Выполнить задание 2.1. с использованием MS Excel. 2.3. Построить с использованием инструмента Описательная статистика Пакета анализа статистический отчет для выборки малого объема. Задание 3. 3.1. Смоделировать с использованием Пакета анализа выборку случайной величины ζ, распределенной по нормальному закону с параметрами m и σ. Значения параметров и объема выборки n следует выбрать в соответствии с последней цифрой шифра из таблицы 1 (случайное рассеивание возьмите равным предпоследней цифре шифра). Таблица 1.
3.2. Выполнить с использованием MS Excel точечное и интервальное оценивание математического ожидания генеральной совокупности по данным выборки, полученной в п. 3.1. Значение доверительной вероятности возьмите равным 0,90. Задание 4. По результатам выполнения заданий 1 и 2 сформулировать и обосновать выводы о том, как изменяется точность найденных параметров в зависимости от объема выборки. Выполнение задания 1.1. Инструмент Генерация случайных чисел Пакета анализа предназначен для проведения статистического моделирования. Для моделирования выборки заданного закона распределения выполните следующие действия: Выберите команду Данные, выберите вкладку Анализ данных. Отроется окно диалога «Анализ данных» (рис. 1). 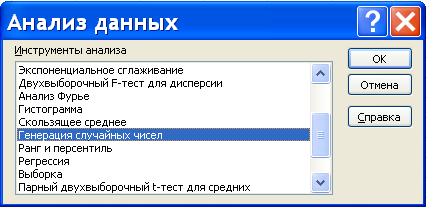 Рис. 1 Окно диалога «Анализ данных» Из списка инструментов анализа выберите Генерация случайных чисел и нажмите кнопку ОК. На экране появится окно диалога «Генерация случайных чисел» (рис. 2). 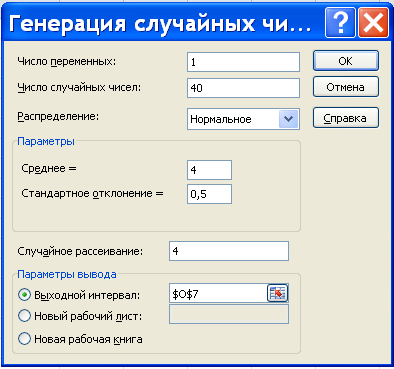 Рис. 2. Окно диалога «Генерация случайный чисел» Введите в поле Число переменных 1 (поскольку требуется смоделировать один закон распределения), а в поле Число случайных чисел – 40 (объём выборки). Закон распределения моделируемой случайной величины задается параметром Распределение: выберите из списка Нормальное. Откроется окно диалога для вводов параметров нормального распределения. Введите в поле Среднее число 4, в поле ввода Стандартное отклонение - 0,5, а в поле Случайное рассеивание – число 4. В разделе «Параметры вывода» установите переключатель Выходной интервал. В одноименном поле укажите ячейку $A$6, начиная с которой будут выводиться на экран выборочные значения. Нажмите кнопку ОК. В столбце А, начиная с ячейки А:, появятся генерируемые значения выборки. Значения ячеек А26:А45 перенесите в ячейки В6:В25 для удобства дальнейшей обработки. Создаваемая электронная таблица представлена в таблице 2 в режиме вычислений и в таблице 3 в режиме формул. Завершая выполнение первого задания, оформите таблицу как указано ниже:
Назовите ярлык рабочего листа Оценки. Выполнение задания 1.2. Для нахождения значений точечных оценок воспользуемся функциями, которые содержатся в категории Статистические. Функция СРЗНАЧ возвращает значение оценки математического ожидания, вычисленное по формуле  , функции ДИСПР и СТАНДОТКЛОНП - значения выборочных дисперсии и стандартного отклонения , функции ДИСПР и СТАНДОТКЛОНП - значения выборочных дисперсии и стандартного отклонения(формулы:  , ,  ). ).Для вычисления значений несмещенной оценки дисперсии и оценки стандартного отклонения по формулам ( 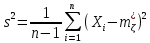 , , 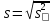 ) воспользуемся функциями ДИСП и СТАНДОТКЛОН соответственно. ) воспользуемся функциями ДИСП и СТАНДОТКЛОН соответственно.Введете формулы для вычисления значений точечных оценок параметров закона распределения для малой выборки в строку 8 (ячейки D8:H8), для большой выборки – в строку 9 (ячейки D9:H9).
Чтобы электронная таблица была удобной для анализа результатов вычислений, введите следующие поясняющие заголовки:
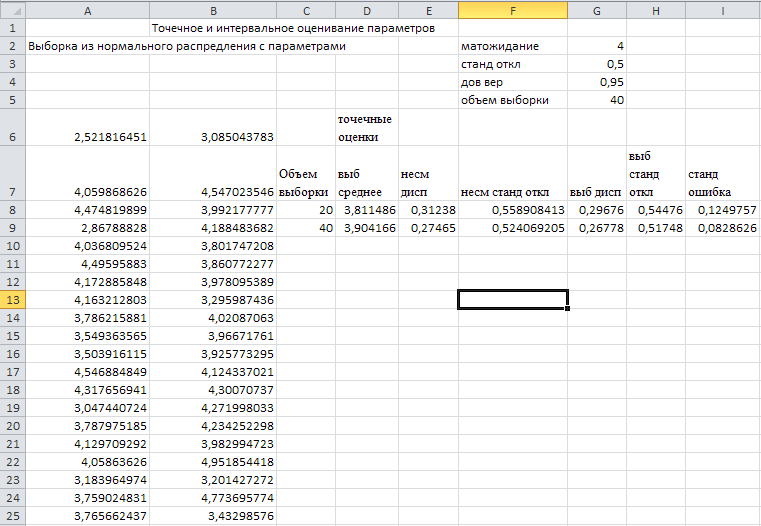 Выполнение задания 2.1. Задача о нахождении доверительного интервала для математического ожидания была решена на практическом занятии. В расчетах следует использовать вычисленные при выполнении задания 1 значения точечных оценок математического ожидания и дисперсии. Выполнение задания 2.2. Доверительный интервал для математического ожидания в случае малой выборки определяется по формуле 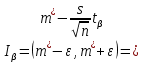 , ,  ). Расчет выполним в ячейках C13:G13. ). Расчет выполним в ячейках C13:G13.Введите значения объемов малой и большой выборок (20 и 40) в ячейки С13 иС14 соответственно. Функция СТЬЮДРАСПОБР возвращает квантиль порядка 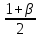 распределения Стьюдента с n-1 степенью свободы распределения Стьюдента с n-1 степенью свободы 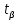 . В качестве аргументов функции следует указать уровень значимости . В качестве аргументов функции следует указать уровень значимости 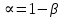 и число степеней свободы. Введите в ячейку D13 формулу =СТЬЮДРАСПОБР(1-$G$4;C13-1). и число степеней свободы. Введите в ячейку D13 формулу =СТЬЮДРАСПОБР(1-$G$4;C13-1).Для вычисления предельной ошибки 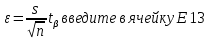 формулу =D3*F8/КОРЕНЬ(С13). формулу =D3*F8/КОРЕНЬ(С13).Нижнюю и верхнюю границы доверительного интервала вычислите в ячейкахF13 и G13.
Расчет границ доверительного интервала для математического ожидания большой выборки по формуле 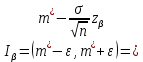 , , 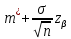 ) выполните в ячейках D14:G14. Для нахождения квантили нормального стандартного распределения порядка ) выполните в ячейках D14:G14. Для нахождения квантили нормального стандартного распределения порядка 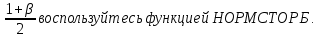 Введите следующие формулы: Введите следующие формулы:
Введите комментарий так, как указано ниже.
Функция ДОВЕРИТ возвращает предельную ошибку для заданной доверительной вероятности. Аргументами этой функции являются уровень значимости, несмещенное стандартное отклонение и объем выборки. Введите в ячейку E15 формулу =ДОВЕРИТ(1-$G$4;F9;C14). Убедитесь в том, что значения ячеек E14 и E15 совпадают. Выполнение задания 2.3. Инструмент Описательная статистика позволяет построит статистический отчет для входных данных (заданной выборки). Выходная таблица содержит два столбца: левый столбец содержит названия статистических данных, правый – статистические данные. Для получения результатов обработки выборки в выходной таблице выполните следующие действия: Выберите команду Данные – Анализ данных – Описательная статистика. В открывшемся окне диалога «Описательная статистика» задайте параметры (рис. 3). Введете входной интервал $A$6:$A$25. Для параметра Группирование установите переключатель по столбцам. Установите флажки Итоговая статистика, Уровень надежности, в одноименное поле введите 95%. В разделе Параметры вывода установите переключатель Выходной интервал и в поле Выходной интервал введите адрес ячейки $D$17. Параметры окна диалога «Описательная статистика» установлены. Нажмите кнопку ОК. На экране появится таблица, созданная инструментом Описательная статистика для заданной выборки. Проделайте тоже самое для объема n=40. Рассмотрите внимательно эту таблицу. Сравните приведенные в ней значения для среднего, дисперсии и стандартного отклонения малой выборки, а также стандартной ошибки с результатами расчетов тех же величин с использованием формул (со значениями в ячейках D8, E8, F8, I8). Уровнем надежности в таблице названа предельная ошибка. В таблице приведены и другие характеристики выборки. Медианой называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Интервалом названа разность между наибольшим и наименьшим значениями выборки. Максимум – это наибольший элемент выборки, а сумма и счет - это сумма значений элементов выборки и ее объем. 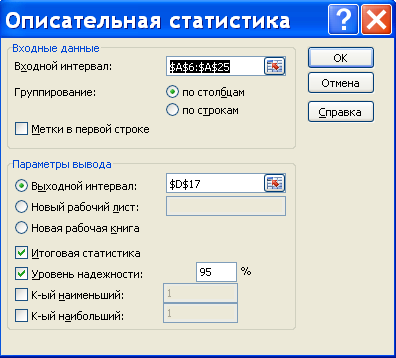 Рис. 3. Диалоговое окно «Описательная статистика» Содержание отчета. Название работы и задание. Результаты ручного счета по заданию 2.1. Две распечатки таблицы, созданной при выполнении задания 3 (одна содержит результаты вычислений, другая – сами формулы). Результаты анализа данных по заданию 4. |
