Контрольная работа 1 по теме Тригонометрические функции
 Скачать 107.11 Kb.
|
|
Контрольные работы по алгебре и началам анализа в 11 классе Контрольная работа № 1 по теме «Тригонометрические функции» Вариант 1  Найдите область определения и множество значений функции у = 2 cos x.Выясните, является ли функция у = sin x – tg x четной или нечетной. Изобразите схематически график функции у = sin x + 1 на отрезке  . Найдите наибольшее и наименьшее значения функции у = 3sin x ∙cos x + 1. Постройте график функции у = 0,5 cos x – 2. При каких значениях х функция возрастает? Убывает?Контрольная работа № 1 по теме «Тригонометрические функции» Вариант 2 Найдите область определения и множество значений функции у = 0,5 cos x.Выясните, является ли функция у = cos x – x2 четной или нечетной. Изобразите схематически график функции у = cos x - 1 на отрезке . Найдите наибольшее и наименьшее значения функции у =  + 1. Постройте график функции у = 2 sin x + 1. При каких значениях х функция возрастает? Убывает?Контрольная работа № 2 по теме «Производная и ее геометрический смысл» Вариант 1 Найдите производную функции: а) 3х2 -  б)  в)  г)  Найдите значение производной функции f(x) =  в точке х0 = 8.Запишите уравнение касательной к графику функции f(x) = sin x – 3x + 2 в точке х0 = 0. Найдите значения х, при которых значения производной функции f(x) =  положительны. Найдите точки графика функции f(x)= х3 – 3х2, в которых касательная к нему параллельна оси абсцисс. Найдите производную функции f(x) =  .Контрольная работа № 2 по теме «Производная и ее геометрический смысл» Вариант 2 Найдите производную функции: а) 2х3 -  б)  в)  г)  Найдите значение производной функции f(x) =  в точке х0 =  .Запишите уравнение касательной к графику функции f(x) = 4x - sin x + 1 в точке х0 = 0. Найдите значения х, при которых значения производной функции f(x) =  отрицательны. Найдите точки графика функции f(x)= х3 + 3х2, в которых касательная к нему параллельна оси абсцисс. Найдите производную функции f(x) = cos  .Контрольная работа № 3 по теме «Применение производной к исследованию функций» Вариант 1 Найдите стационарные точки функции f(x) = х3- 2х2 +х +3.Найдите экстремумы функции: а) f(x) =х3 – 2х2 + х + 3; б) f(x) =  .Найдите интервалы возрастания и убывания функции f(x) = х3- 2х2 +х +3. Постройте график функции f(x) = х3- 2х2 +х +3 на отрезке  . Найдите наибольшее и наименьшее значения функции f(x) = х3- 2х2 +х +3 на отрезке  . Среди прямоугольников, сумма длин трех сторон которых равна 20, найдите прямоугольник наибольшей площади.Контрольная работа № 3 по теме «Применение производной к исследованию функций» Вариант 2 Найдите стационарные точки функции f(x) = х3- х2 - х +2.Найдите экстремумы функции: а) f(x) = х3- х2 - х +2; б) f(x) =  .Найдите интервалы возрастания и убывания функции f(x) = х3- х2 - х +2. Постройте график функции f(x) = х3- х2 - х +2 на отрезке . Найдите наибольшее и наименьшее значения функции f(x) = х3- х2 - х +2 на отрезке . Найдите ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.Контрольная работа № 4 по теме «Интеграл» Вариант 1 Докажите, что функция F(x) = 3х + sin x – e2xявляется первообразной функции f (x) = 3 + cos x – 2e2x на всей числовой оси.Найдите первообразную F функции f (x) = 2  , график которой проходит через точку А(0;  ).Вычислите площадь фигуры, изображенной на рисунке. 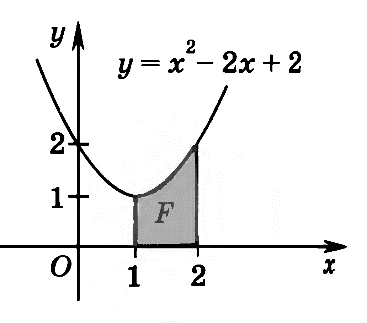 Вычислить интеграл: а)  dx; б)  . Найдите площадь фигуры, ограниченной прямой у = 1 – 2х и графиком функции у = х2 – 5х – 3.Контрольная работа № 4 по теме «Интеграл» Вариант 2 Докажите, что функция F(x) = х + cos x + e3xявляется первообразной функции f (x) = 1 - sin x + 3e3x на всей числовой оси.Найдите первообразную F функции f (x) = - 3  , график которой проходит через точку А(0;  ).Вычислите площадь фигуры, изображенной на рисунке. 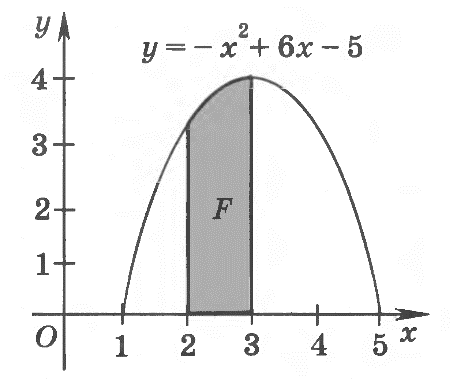 Вычислить интеграл: а)  dx; б)  . Найдите площадь фигуры, ограниченной прямой у = 3 – 2х и графиком функции у = х2 + 3х – 3. |