Контрольная работа по геометрии. Контрольная работа 1 Вариант 1 Задает ли указанное правило функцию в случае положительного ответа
 Скачать 89.03 Kb.
|
|
Контрольная работа № 1 Вариант 1 1. Задает ли указанное правило функцию 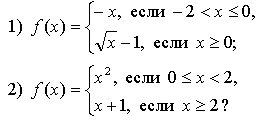  В случае положительного ответа: а) найдите область определения функции; б) вычислите значения функции в точках 0, 1, 3, –1; в) постройте график функции; г) найдите промежутки монотонности функции. 2. Исследуйте функцию  на четность.3. На числовой окружности взяты точки  Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.4. Задайте аналитически и постройте график функции  у которой  5. Найдите функцию, обратную функции  Постройте на одном чертеже графики этих взаимно обратных функций.Вариант 2 1. Задает ли указанное правило функцию 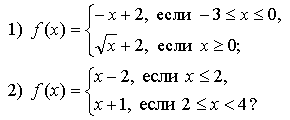 В случае положительного ответа: а) найдите область определения функции; б) вычислите значения функции в точках –4, –2, 0, 4; в) постройте график функции; г) найдите промежутки монотонности функции. 2. Исследуйте функцию  на четность.3. На числовой окружности взяты точки  Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.4. Задайте аналитически и постройте график функции у которой  5. Найдите функцию, обратную функции  Постройте на одном чертеже графики этих взаимно обратных функций.Решение контрольной работы Вариант 1 1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции. В случае 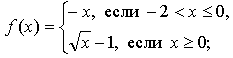 условия не соблюдаются: f(0) = 0 и f(0) = –1. 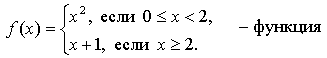  б) 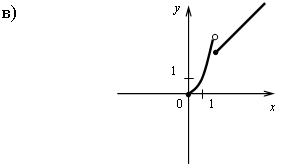 – не определено; г) на [0; 2) и на [2; +) функция возрастает, в точке х = 2 функция имеет разрыв. 2. 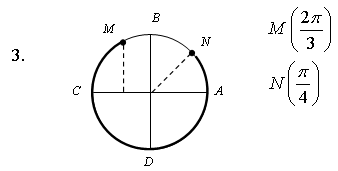 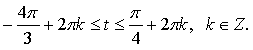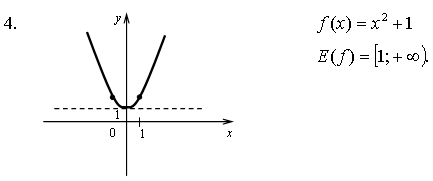– симметрична относительно начала координат. значит, функция f(х) – нечетная.   5. у = 2 – х2 Квадратичная функция определена и убывает при х 0, значит, существует обратная функция: у = 2 – х2;  Функция 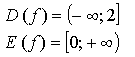 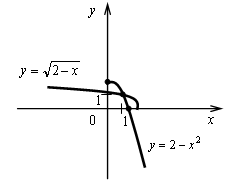  Вариант 2 1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции. В случае 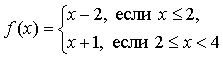 условия не соблюдаются: f(2) = 0 и f(2) = 3. 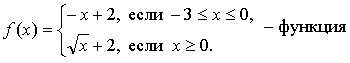  б) f(–4) – не определено; 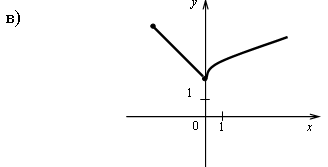   г) на 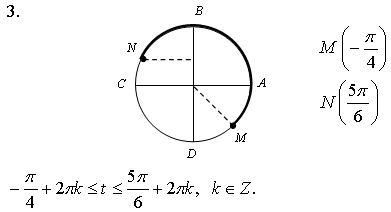 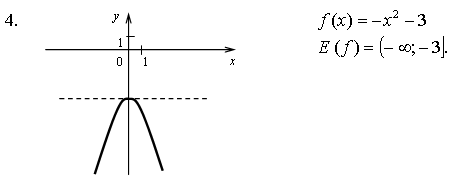функция убывает; на  функция возрастает.2.  – не симметрична относительно начала ординат, значит, функция ни четная, ни нечетная.  5. у = х2 + 7. Квадратичная функция определена и возрастает при х 0, значит, существует обратная функция: у = х2 + 7;  Функция 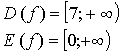 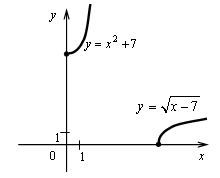  |