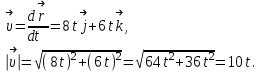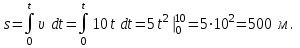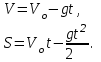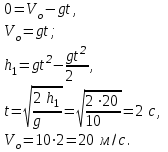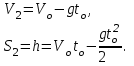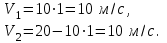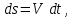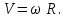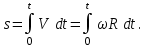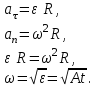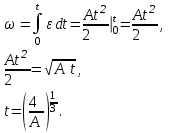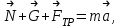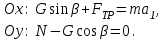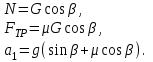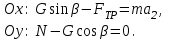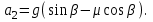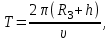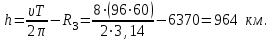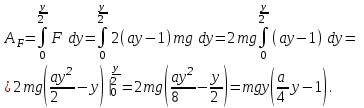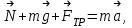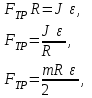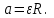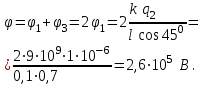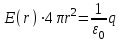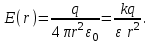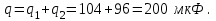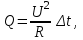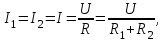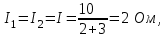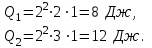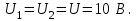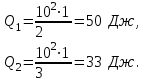контрольная работа по физике. Контрольная работа 1 вариант 2. Задачи 102 112 122 132 142 152 162 172 182. Задача 102

• Название: Контрольная работа 1 вариант 2. Задачи 102 112 122 132 142 152 162 172 182. Задача 102
• Анкор: контрольная работа по физике
• Дата: 09.12.2020
• Размер: 197.95 Kb.
• Имя файла: Physics_002.docx
• Тип: Контрольная работа; #158970

Контрольная работа №1 вариант №2.

Задачи: 102; 112; 122; 132; 142; 152; 162; 172; 182.
Задача №102.
Радиус-вектор частицы определяется выражением 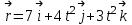. Найти: а) модуль перемещения тела за первые t = 10 с после начала перемещения; б) путь S, пройденный телом за это время.
Решение:
а) определяем модуль перемещения


б) определяем модуль скорости частицы


Определяем путь, пройденный телом за это время


Ответ: а) |r| = 500 м; s = 500 м.


Задача №112.

Тело брошено вертикально вверх с начальной скоростью V_o и достигло высшей точки подъема h₁ = 20 м над поверхностью Земли. В этот момент с той же точки вертикально вверх брошено второе тело с той же начальной скоростью. Найти: а) величину начальной скорости V_o; б) высоту h, на которой тела встретятся; в) время встречи t_o; г) скорости тел V₁ и V₂ в момент встречи.
Решение:
а) запишем выражения для определения перемещения и скорости тела, брошенного вертикально вверх (a = -g)

(1) (2)

где t – время движения тела, с;

g = 10 м/с² – ускорение свободного падения.
Решая систему уравнений (1)-(2) для высшей точки подъема (S = h₁), определим начальную скорость V_o. В высшей точке подъема V₁ = 0, поэтому


б-г) первое и второе тела встретятся на некоторой высоте h. При этом для первого тела, падающего с высоты h₁, уравнения (1) и (2) примут вид

(3) (4)

Откуда

(5)

Для второго тела, брошенного вверх с начальной скоростью V_o

(6) (7)

Приравнивая правые части уравнений (5) и (7), получаем


Определяем скорости тел в момент их встречи t_o по выражениям (3) и (6)



Ответ: а) V_o = 20 м/с; б) h = 15 м; в) t_о = 1 с; г) V₁ = 10 м/с, V₂ = 10 м/с.


Задача №122.

Материальная точка начинает двигаться по окружности радиусом R = 6 м с угловым ускорением ε = Аt, где А – постоянная. Найти путь S, пройденный точкой к моменту времени, когда ее тангенциальное и нормальное ускорение станут равными друг другу.
Решение:
Путь, пройденный точкой, определяется выражением

(1)

где V - линейная скорость точки, м/с,

где ω - угловая скорость точки, с^-1.
Интегрируя обе части уравнения (1), получим

(3)

Так как a_τ = a_n, то

(4)

Определяем момент времени t, когда a_τ = a_n

(5)

Решаем интегральное уравнение (3)


Ответ: s = 8 м.

Задача №132.

Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол β = 15^о с горизонтом. Время подъема тела оказалось в два раза меньше времени спуска. Найти коэффициент трения тела о плоскость. Принять tg 15^o = 0,268. Ответ округлить до сотых.
Решение:

Р 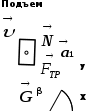асчетная схема выглядит следующим образом

Условие равновесия для тела при подъеме и спуске

где N – нормальная реакция опоры, Н;

G - сила тяжести бруска, Н;

F_тр – сила трения, Н.
Проецируя действующие силы на оси выбранной системы координат, для подъема получим

(1) (2)

Сила трения выражается через реакцию опоры

(3)

Решая совместно систему уравнений (1)-(3), определяем a₁

(4)

Проецируя действующие силы на оси выбранной системы координат, для спуска получим

(5) (6)

Решая совместно систему уравнений (3), (5) и (6), определяем a₂

(7)

Перемещение тела при подъеме s₁ и s₂ определяется выражениями

(8) (9)

где t₁ и t₂=2t₁ – время подъема и спуска соответственно.
Решаем систему уравнений (4), (7), (8) и (9) относительно µ при условии s₁ = s₂


Ответ: µ = 0,16.

Задача №142.

Первый искусственный спутник Земли, запущенный в 1957 году в СССР, имел скорость 8 км/с и период обращения Т = 96 мин. Найти высоту подъема спутника, полагая его орбиту круговой. Радиус Земли R₃ = 6370 км.
Решение:

Период обращения спутника определяем по уравнению

(1)

где h – высота подъема спутика, м.
Решаем уравнение (1) относительно h


Ответ: h =964 км.

Задача №152.

Тело массой m начинают поднимать с поверхности Земли, приложив к нему силу F, которую изменяют с высотой подъема y по закону F = 2(ay-1)mg, где a - положительная постоянная. Найти работу этой силы на первой половине пути подъема.
Решение:

Работа силы определяется выражением

(1)

В нашем случае



Ответ: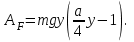


Задача №162.

В момент, когда скорость свободно падающего тела составила V = 2 м/с, оно разорвалось на два одинаковых осколка. Один из осколков полетел в горизонтальном направлении со скоростью V₁ = 3 м/с. Найти скорость V₂ второго осколка сразу после взрыва.
Решение:

Запишем закон сохранения импульса для данной задачи

(1)

где m, m₁ и m₂ - массы соответственно тела до разрыва и первого и второго осколков после разрыва, кг.
Так как m₁ = m₂ = 0,5m, то


Ответ: V₂ = 1 м/с.


Задача №172.

Однородный диск радиусом R скатывается без скольжения по наклонной поверхности, составляющей угол α с горизонтом. Найти угловое ускорение диска.
Решение: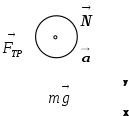




Условие равновесия для диска

где N – нормальная реакция опоры, Н;

G - сила тяжести диска, Н;

F_тр – сила трения, Н.
Проецируя действующие силы на оси выбранной системы координат, получаем

(1)

Определим силу трения, используя закон сохранения энергии для движущегося диска

(2)

где J = mR²/2 - момент инерции сплошного диска, кг·м²;

ε - угловое ускорение диска, с^-2.
Линейное ускорение диска

(3)

Решаем систему уравнений (1)-(3) относительно ε

Ответ:

Задача №182.

Однородный тонкий стержень массой m₁ = 2 кг и длиной l = 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через середину стержня. В нижний конец стержня попадает пластилиновый шарик, летящий горизонтально перпендикулярно стержню со скоростью V = 10 м/с. Масса шарика равна m₂ = 10 г. Найти угловую скорость стержня сразу после попадания шарика.
Решение:
Расчетная схема для решения задачи приведена ниже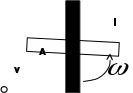


Запишем закон сохранения импульса для данной системы

(1)

где V₁ – скорость стержня с пулей, м/с,

где ω – угловая скорость стержня с пулей, рад/с.
Решаем уравнение (1) относительно ω



Ответ: ω = 0,1 с^-2.

Контрольная работа №3 вариант №2.

Задачи: 302; 312; 322; 332; 342; 352; 362; 372.
Задача №302.

На линии, соединяющей два положительных точечных заряда величинами q₁ = 2q и q₂ = q, расположен положительный заряд q₃ = q. Найти расстояние х от заряда q₁, на котором третий заряд будет находиться в положении равновесия. Расстояние между крайними зарядами r = 10 см .
Решение:

По условию задачи заряд q₃ находится в положении равновесия, то есть

(1)

где F₁₃ и F₂₃ - соответственно силы взаимодействия зарядов q₁ и q₃ и зарядов q₂ и q₃

		(2)
		(3)

Решаем систему уравнений (1)-(3) относительно х


Ответ:

Задача №312.

Четыре точечных заряда расположены в вершинах квадрата со сторонами l. Найти напряженность Е и потенциал φ электрического поля в центре квадрата, если q₁ = q₂ = q₃ = q, q₄ = - q. Заряд q = 1,0 мкКл, l = 10 см.
Решение:

Применяем принцип суперпозиции напряженностей, определяя векторную сумму напряженностей в центре квадрата. Так как заряды q₁ и q₃ расположены в вершинах квадрата на одной диагонали (то есть на равном расстоянии от его центра) и имеют одинаковые знаки, то они не влияют на напряженность в центре квадрата, компенсируя напряженности друг друга. Напротив, так как заряды q₂ и q₄ имеют разные знаки, то вектора их напряженностей направлены в одну сторону. Учитывая, что расстояние от вершины квадрата до его центра x = l·cos45⁰, определяем напряженность в центре квадрата


где k = 9·10⁹ Н·м²/Кл² - коэффициент пропорциональности.
Применяем принцип суперпозиции потенциалов, определяя алгебраическую сумму потенциалов в центре квадрата. Так как заряды q₂ и q₄ имеют разные знаки, то алгебраическая сумма их потенциалов равна нулю. Заряды q₁ и q₃ имеют одинаковые знаки. Определяем потенциал в центре квадрата


Ответ: Е = 3,6·10⁶ Н/м; φ = 2,6·10⁵ В.

Задача №322.

На поверхности тонкой сферы радиусом R равномерно распределен отрицательный заряд q₁ = -q. В центре сферы находится точечный положительный заряд q₂ = +q. Найти напряженность E(r) электрического поля как функцию расстояния r от центра сферы.
Решение:
Определим напряженность поля заряженной сферы по теореме Остроградского-Гаусса.

В случае со сферой поле будет центрально симметричным, то есть вектор Е в любой точке шара проходит через его центр, а величина напряженности является функцией расстояния от центра сферы.

В случае r ≥ R внутрь поверхности сферы радиуса r попадает весь заряд, распределенный по ее поверхности, тогда теорема Остроградского-Гаусса примет вид

где S = 4πr² - площадь поверхности сферы;

ε_о - электрическая постоянная;


Внутри сферы (r < R) не содержится электрический заряд, поэтому Е = 0.

График зависимости E(r) для сферы будет выглядеть следующим образом:


Задача №332.

Три конденсатора соединены последовательно и присоединены к источнику напряжения. Найти заряд и напряжение на третьем конденсаторе.
Решение:
Схема цепи приведена ниже



При последовательном соединении конденсаторов:

- общее напряжение батареи

(1)

- заряд батареи


Учитывая, что U=q/C, решаем уравнение (1) относительно q


Соответственно заряд на третьем конденсаторе равен q₃ = q = 120 Кл.
Напряжение на третьем конденсаторе будет равно


Ответ: q₃ = 120 Кл; U₃ = 40 В.

Задача №342.

Конденсатор емкостью С₁ = 4 мкФ, заряженный до напряжения U₁ = 26 В, соединяют параллельно с конденсатором емкостью С₂ = 6 мкФ, заряженным до напряжения U₂ = 16 В, обкладками, имеющими одинаковые по знаку заряды. Определить напряжение на конденсаторах после их соединения.
Решение:
Определяем величины зарядов на обкладках конденсаторов до их соединения


Определяем емкость и заряд батареи после соединения конденсаторов


При последовательном соединении


Ответ: U₁ = U₂ = 20 В.

Задача №352.
Ток в проводнике за 2с изменился от 8 А до 2 А. Найти заряд, прошедший за это время через поперечное сечение проводника.
Решение:


Ответ: q = 12 Кл.


Задача №362.

Три источника тока с ЭДС ε₁ = 11 В, ε₂ = 4 В, ε₃ = 6 В и три реостата с сопротивлением R₁ = 5 Ом, R₂ = 10 Ом и R₃ = 2 Ом соединены, как показано на схеме. Определить с помощью правила Киргхофа силу тока I₃ через сопротивление R₃. Внутреннее сопротивление источников тока пренебрежимо мало.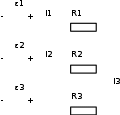




Решение:

По правилам Киргхофа

(1) (2) (3)

Подставляя числовые значения в формулы (2) и (3), получаем

(4) (5)

Решаем уравнение (5) относительно I₁ и далее уравнение (4) относительно I₂

Последовательно находим значения I₁ и I₃


Ответ: I₃ = 0,5 А.

Задача №372.

Имеются два проводника с сопротивлением R₁= 2 Ом и R₂ = 3 Ом. К проводникам подключено внешнее напряжение U = 10 В. Найти количество теплоты Q, выделяющееся в каждом проводнике за время t = 1 с, если проводники соединены: а) последовательно; б) параллельно.
Решение:
Количество тепла, выделяющееся в проводнике определяем по закону Джоуля-Ленца. Используем этот закон:

- для последовательного соединения в виде формулы

(1)

- для параллельного соединения в виде формулы

(2)

где I – сила тока, проходящего через проводник, А.
а) последовательное соединение

При последовательном соединении сила тока, проходящего через проводник, равна

где R = R₁ + R₂ = 2 + 3 = 5 Ом – сопротивление цепи;


а) параллельное соединение

При параллельном соединении напряжения на проводниках одинаковы


Ответ: а) Q₁ = 8 Дж, Q₂ = 12 Дж; б) Q₁ = 50 Дж, Q₂ = 33 Дж.