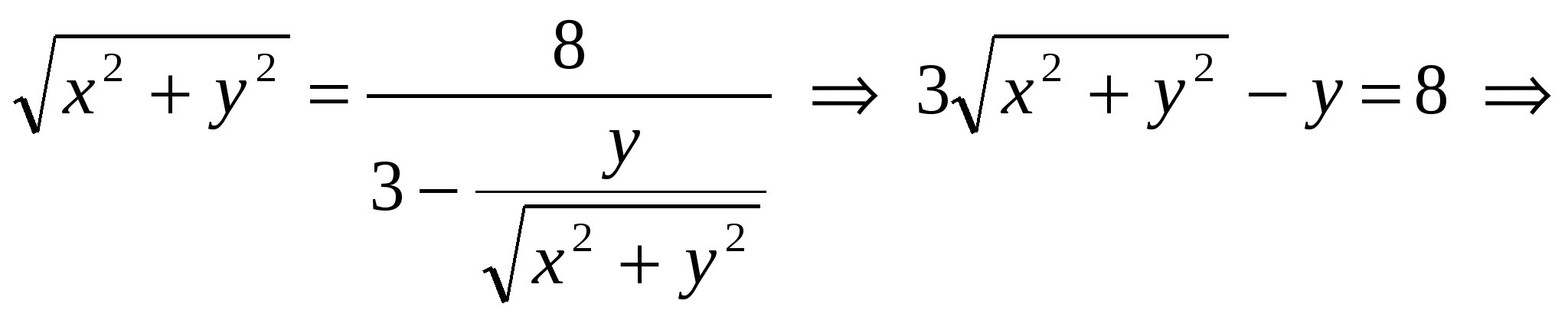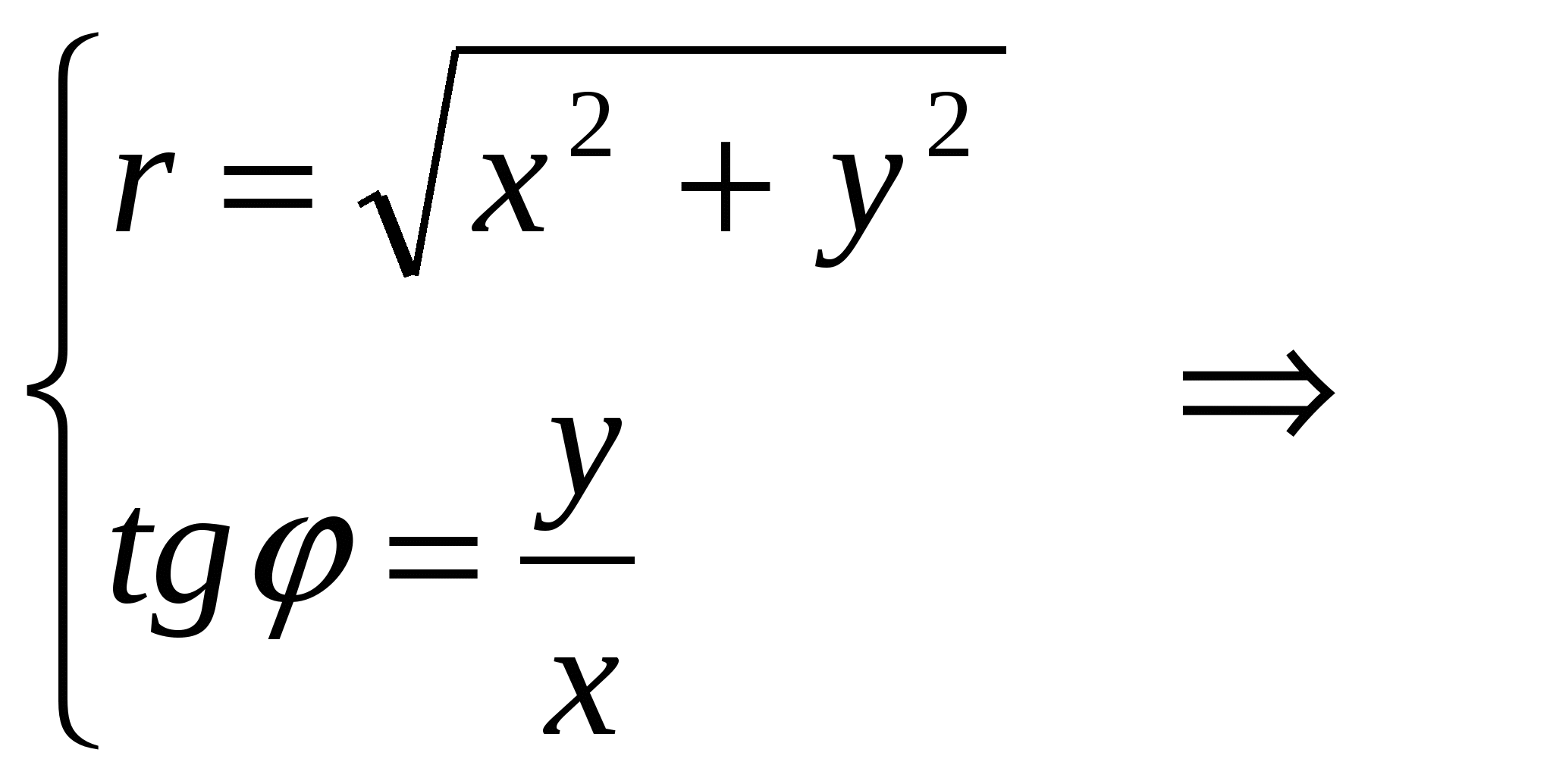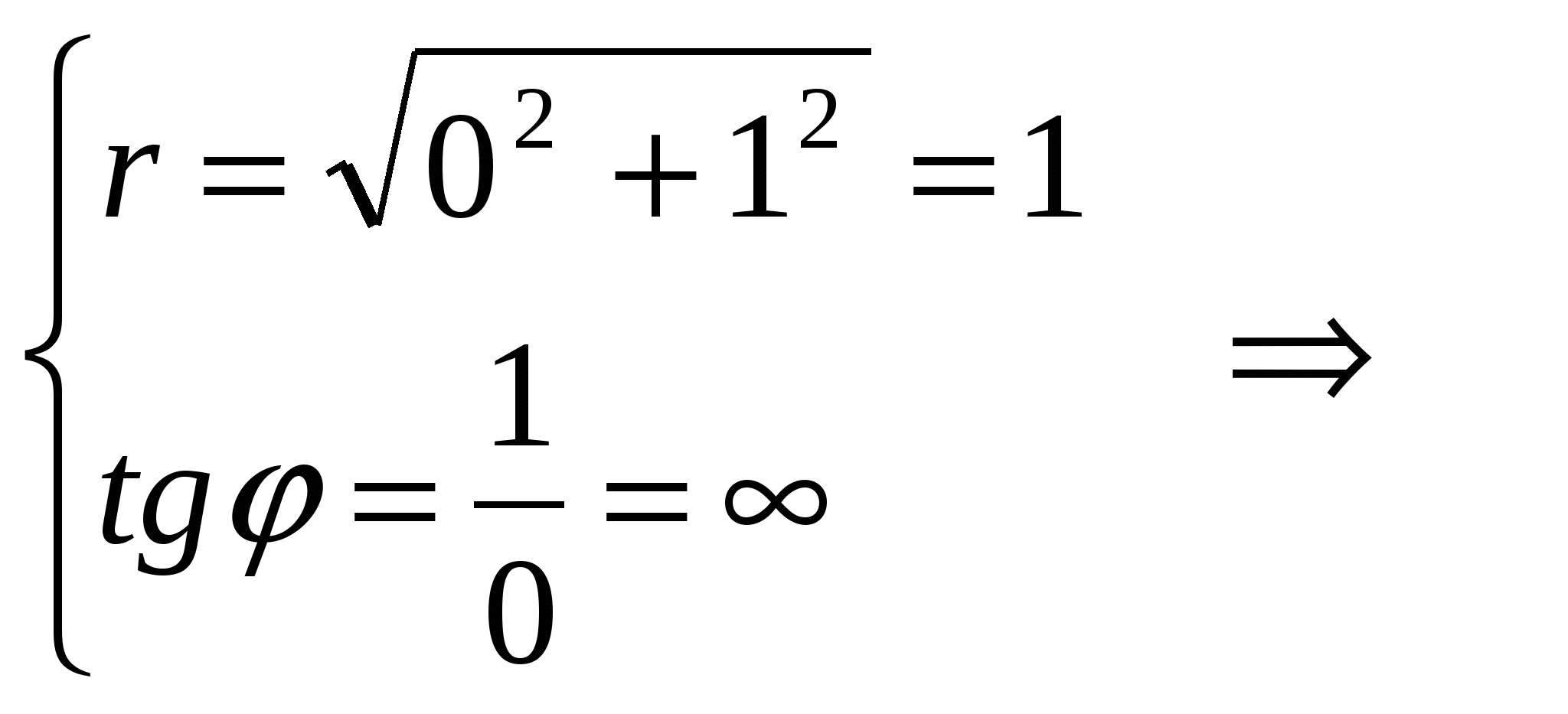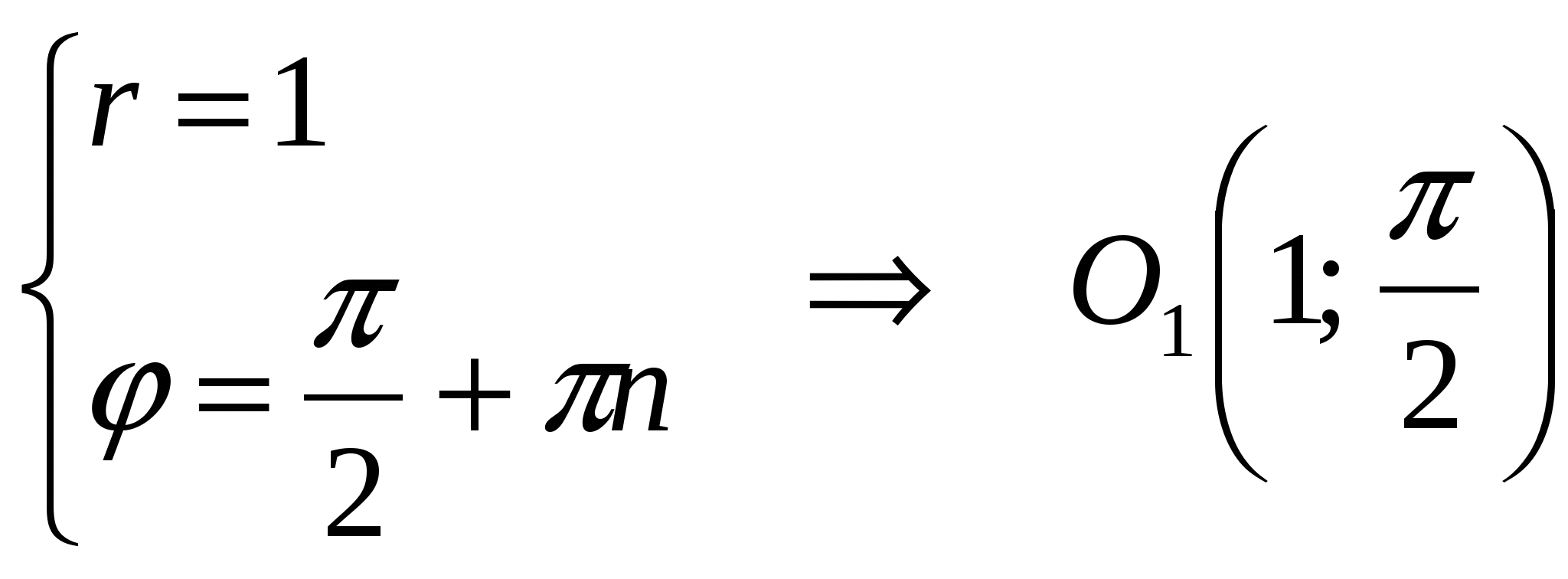Контрольная работа №1
Вариант 8
Задача 1. Даны координаты вершин треугольника 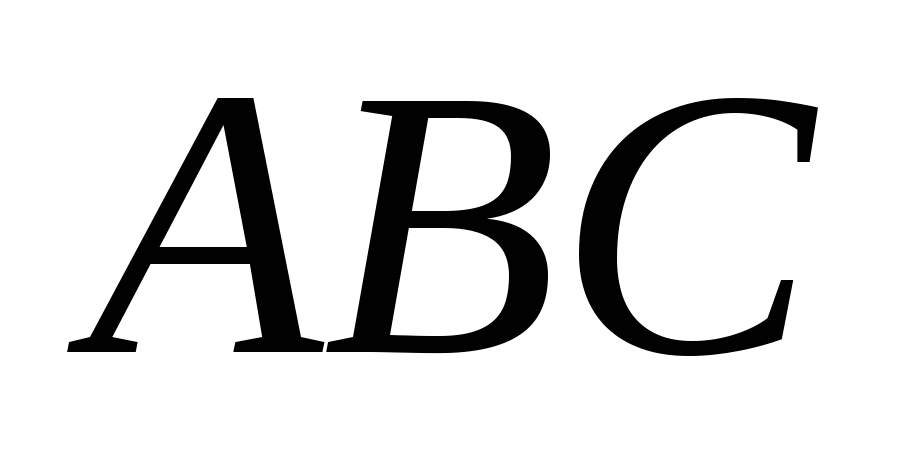 : : 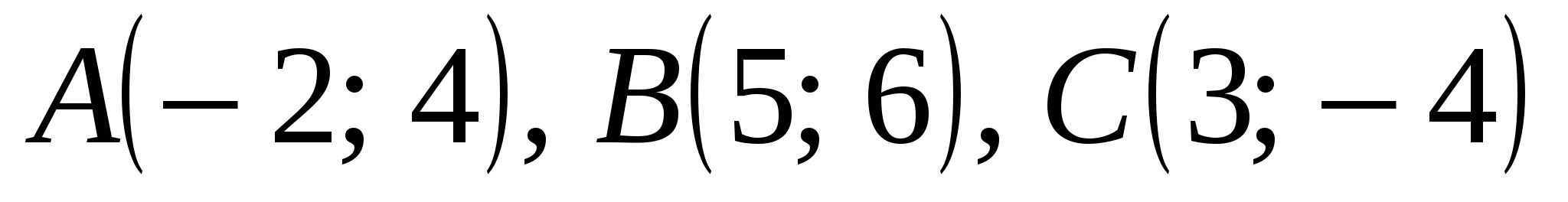 . Требуется: . Требуется:
1) вычислить длину стороны  ; ;
2) составить уравнение стороны  ; ;
3) найти внутренний угол треугольника при вершине 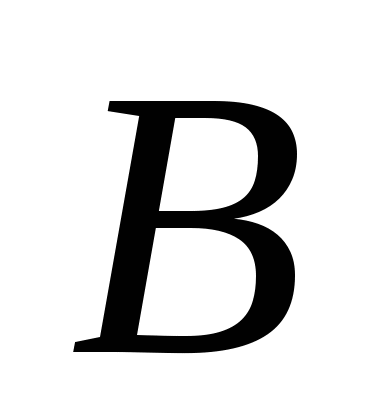 ; ;
4) составить уравнение высоты 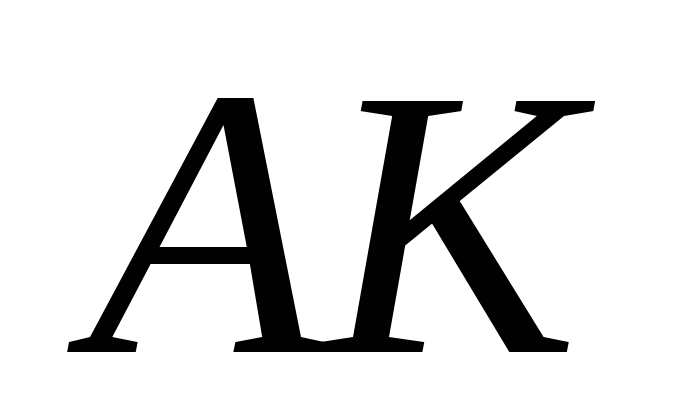 , проведенной из вершины , проведенной из вершины  ; ;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Решение
1) Вычислим длину стороны 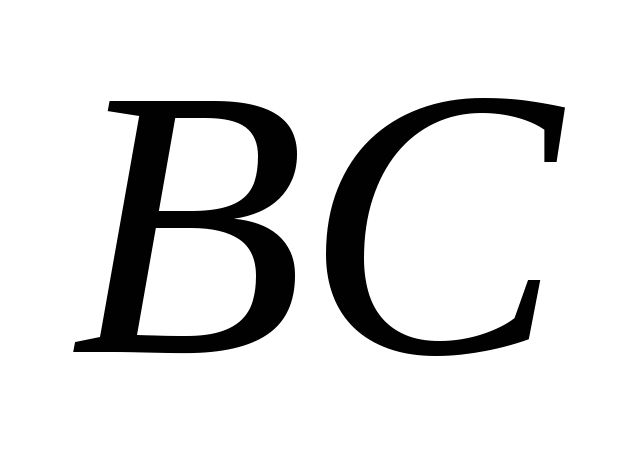 по формуле : по формуле :
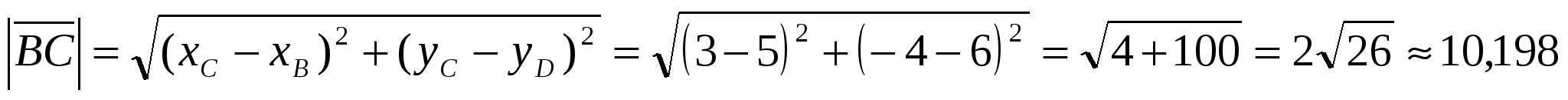
2) Составим уравнение стороны  , использую формулу: , использую формулу:
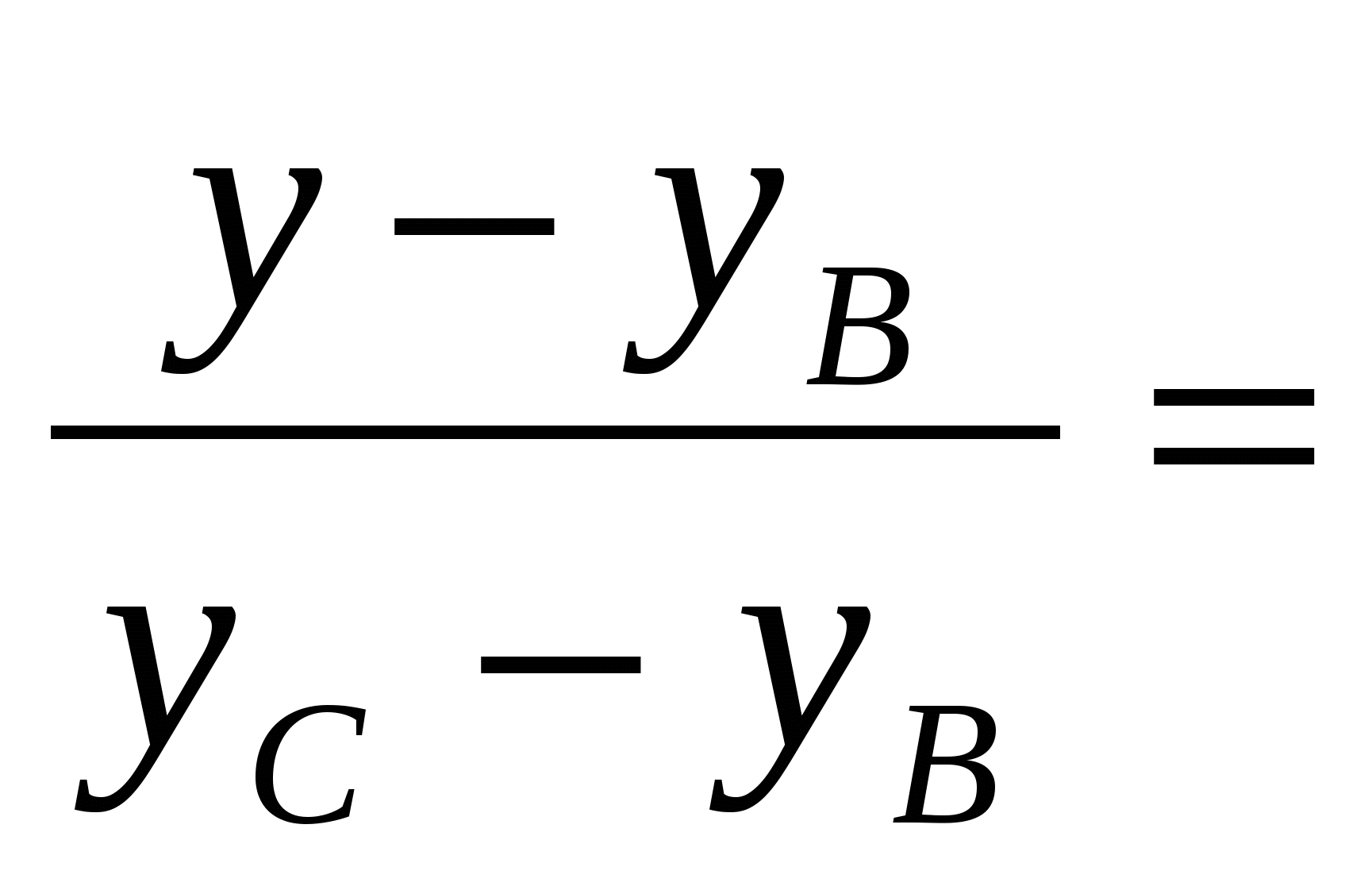 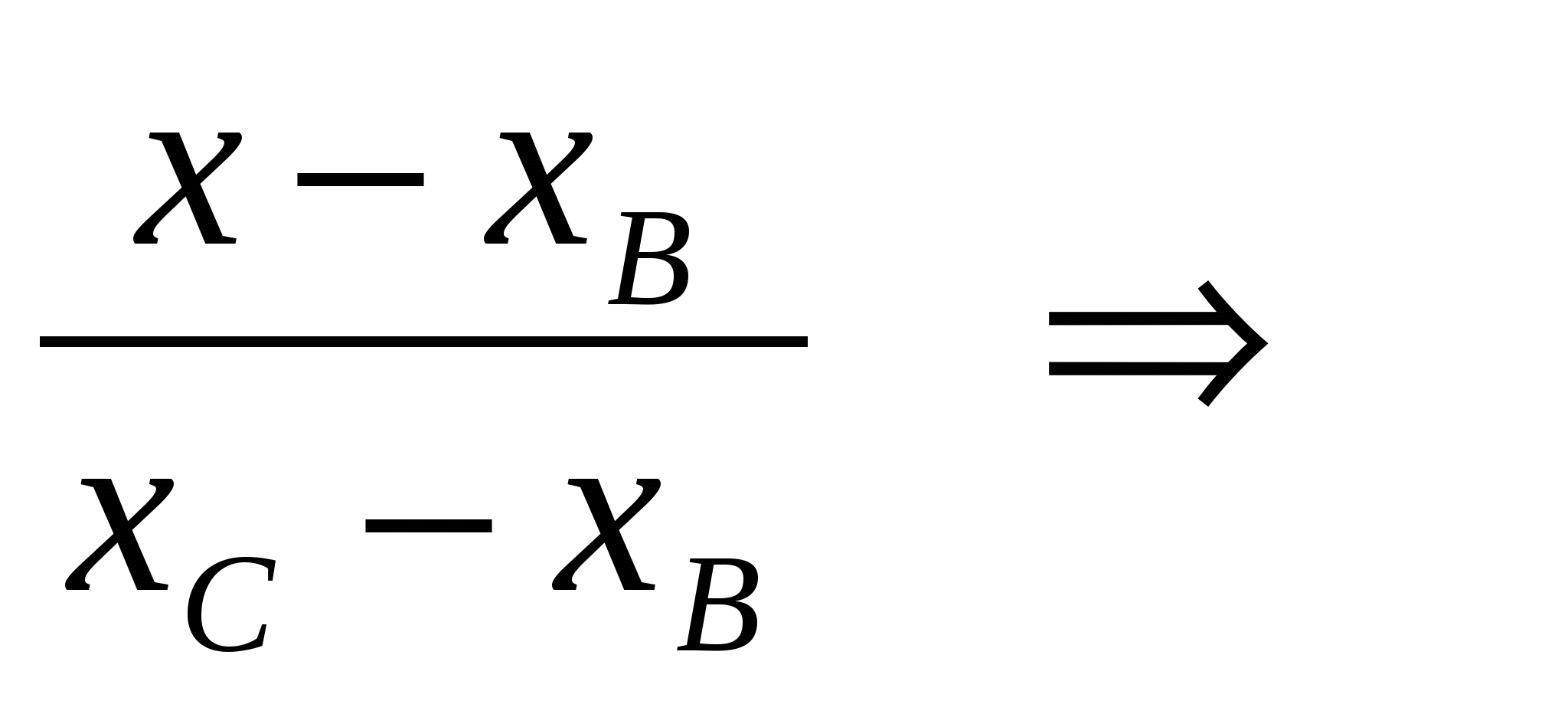 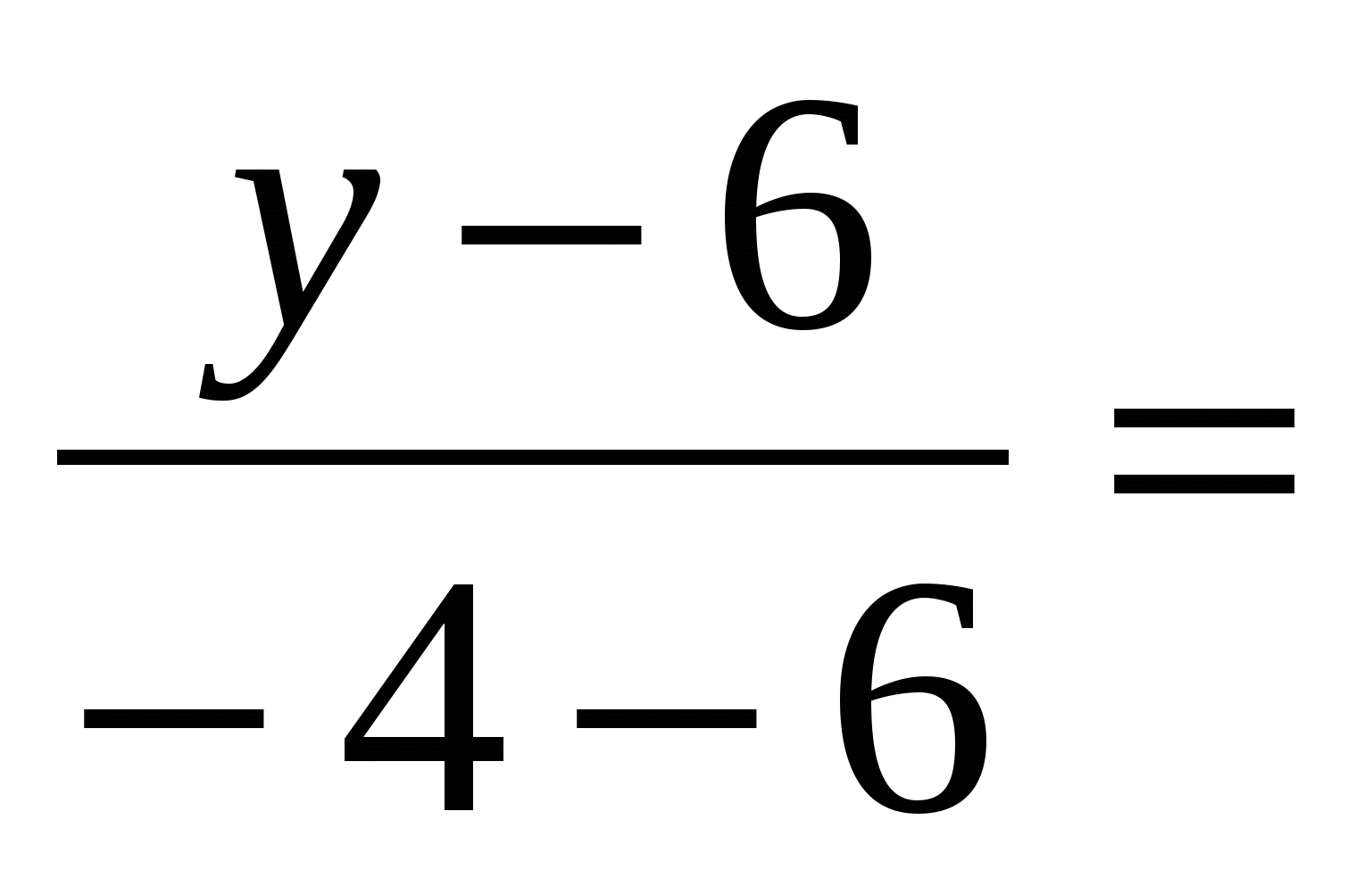 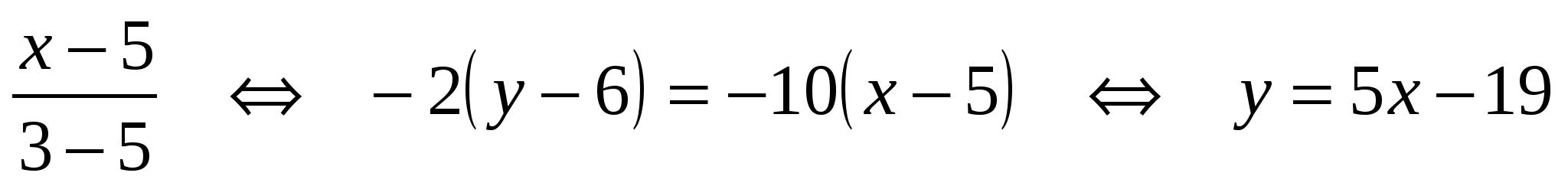 - уравнение - уравнение 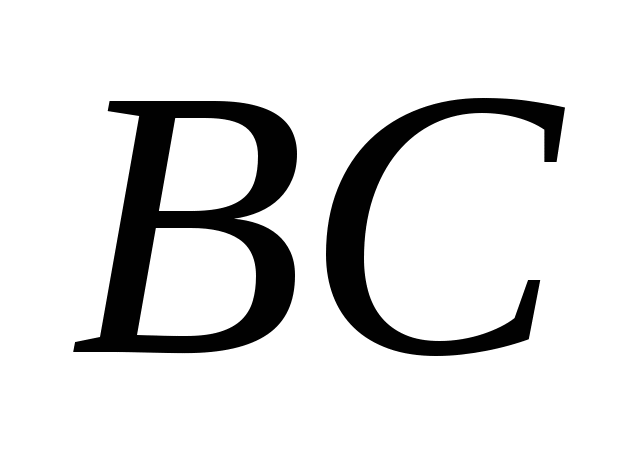
3) Внутренний угол треугольника при вершине 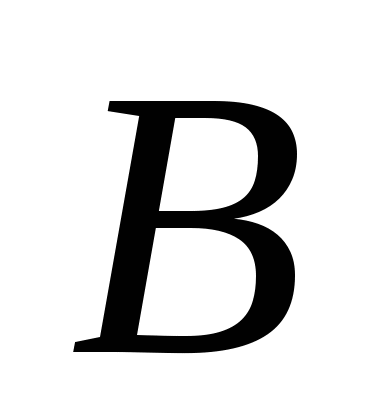 найдем как угол между прямыми найдем как угол между прямыми 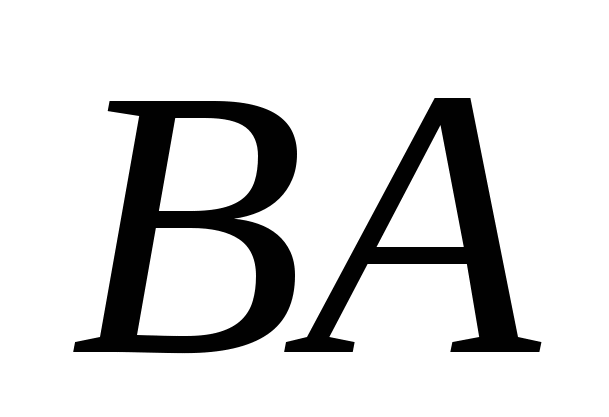 и и 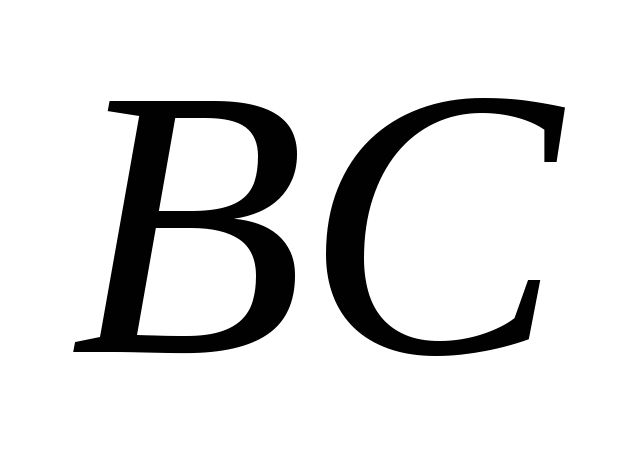 . Для чего сначала вычислим угловой коэффициент . Для чего сначала вычислим угловой коэффициент 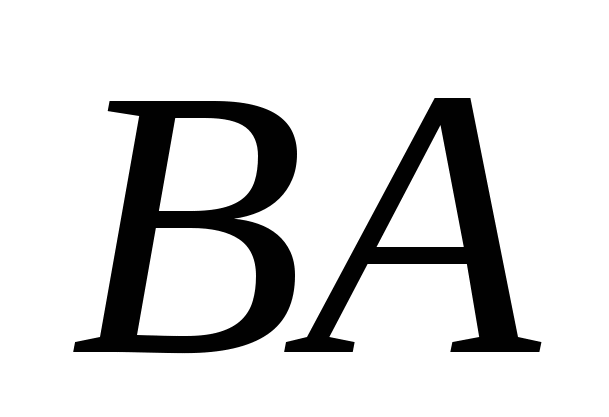 по формуле: по формуле:
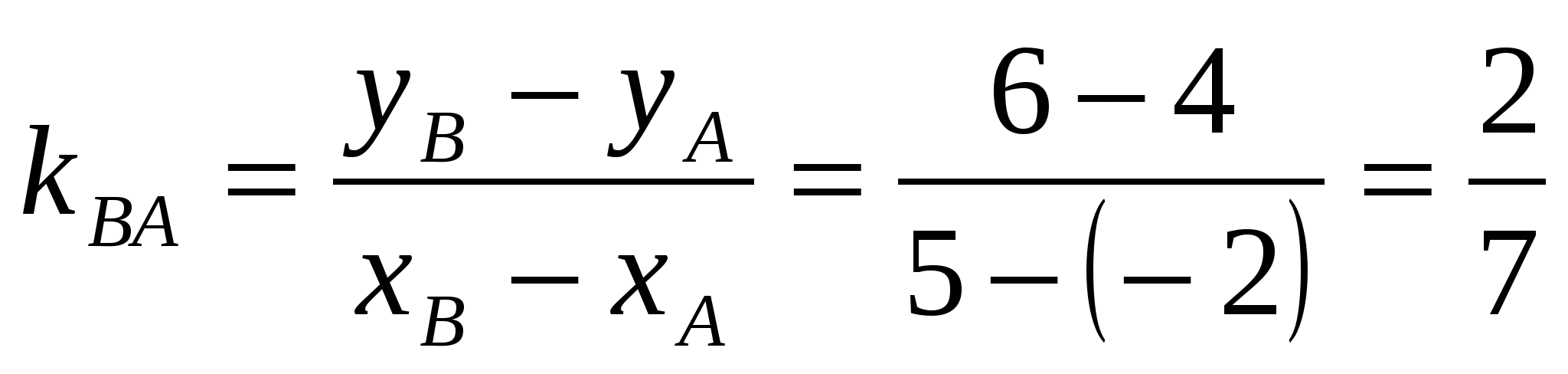
и возьмем из уравнения 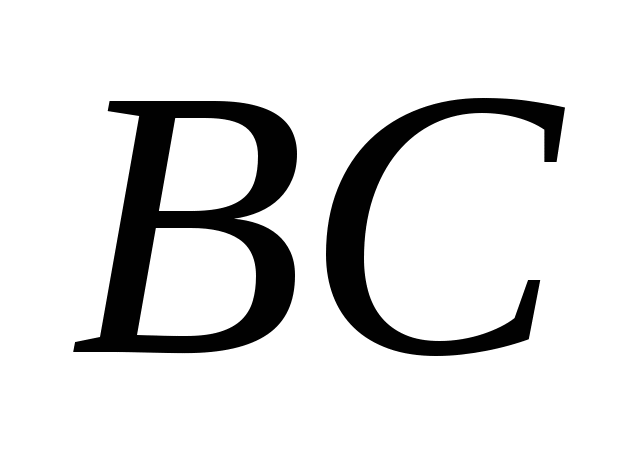 угловой коэффициент прямой угловой коэффициент прямой 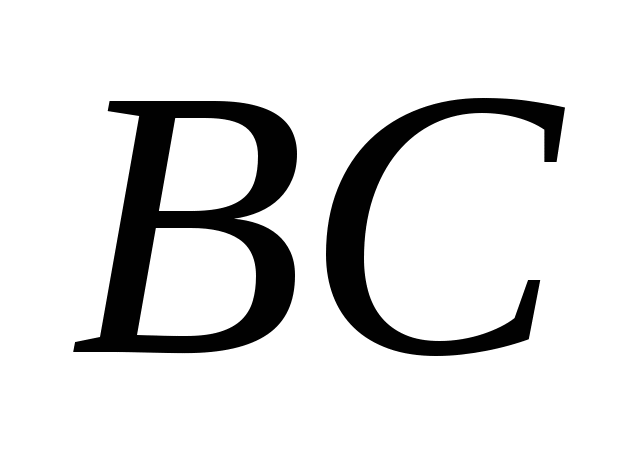 : : 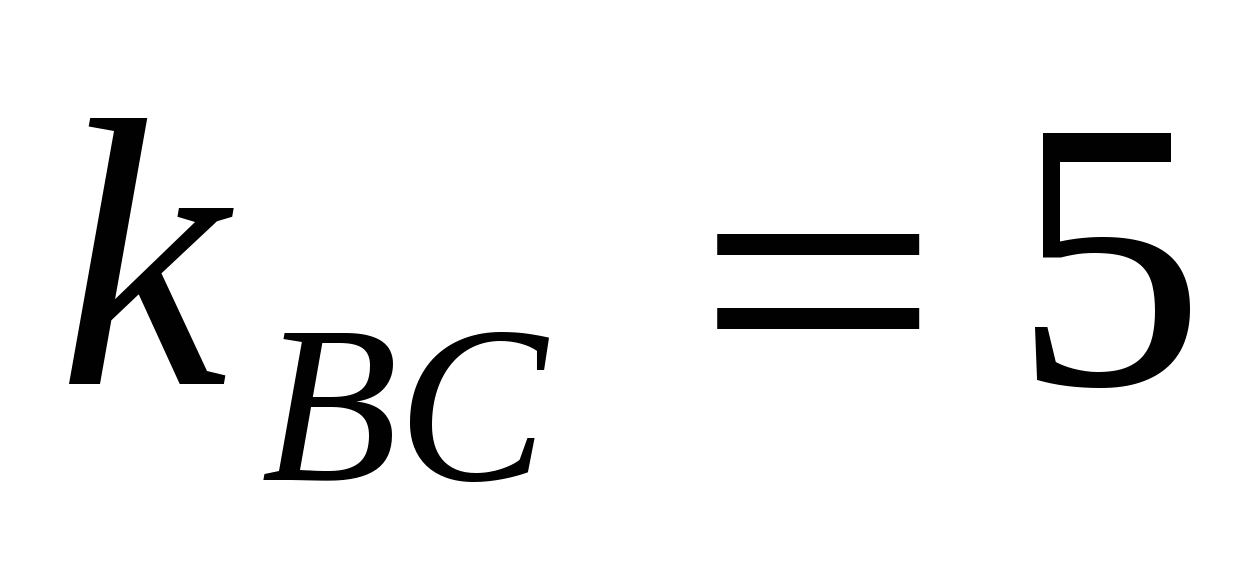
Из расположения точек 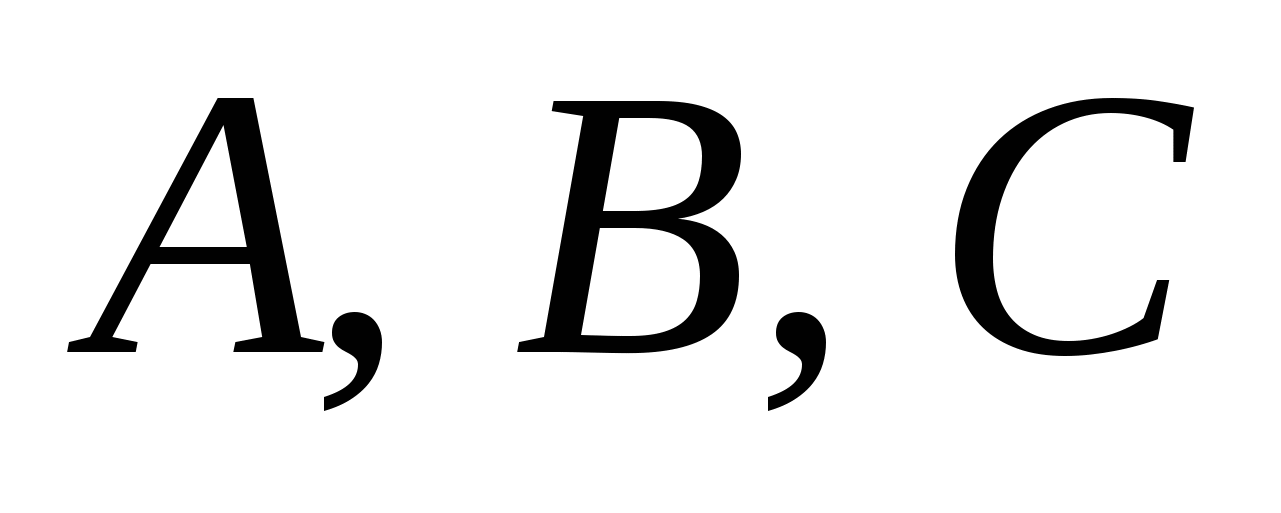 на координатной плоскости видно, что угол на координатной плоскости видно, что угол 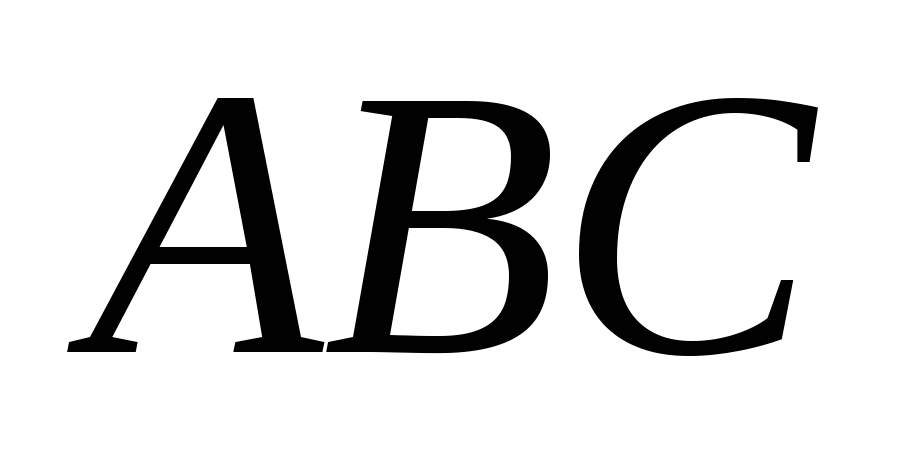 - острый, поэтому вычислим по формуле: - острый, поэтому вычислим по формуле:
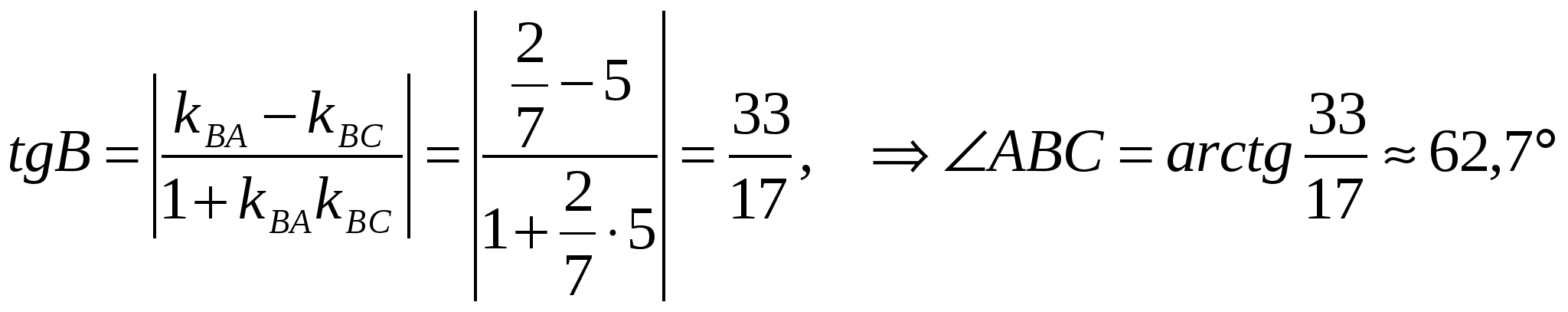
4) Для получения уравнения высоты 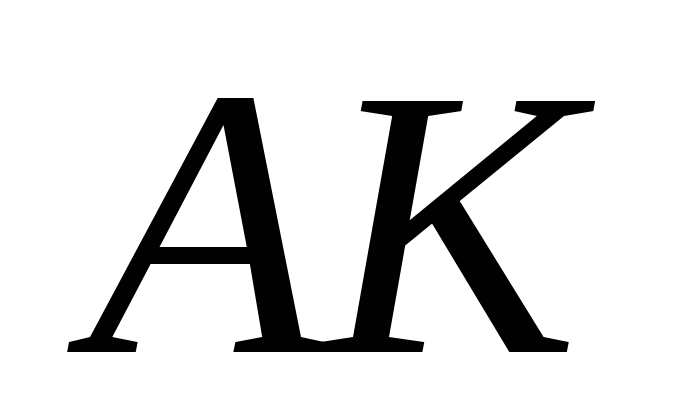 , проведенной из вершины , проведенной из вершины  , используем уравнение пучка прямых и условие перпендикулярности прямых. Сначала вычислим угловой коэффициент прямой , используем уравнение пучка прямых и условие перпендикулярности прямых. Сначала вычислим угловой коэффициент прямой 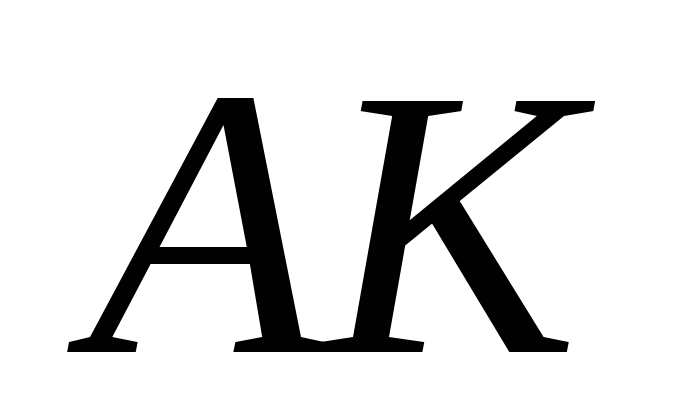 . Так как . Так как 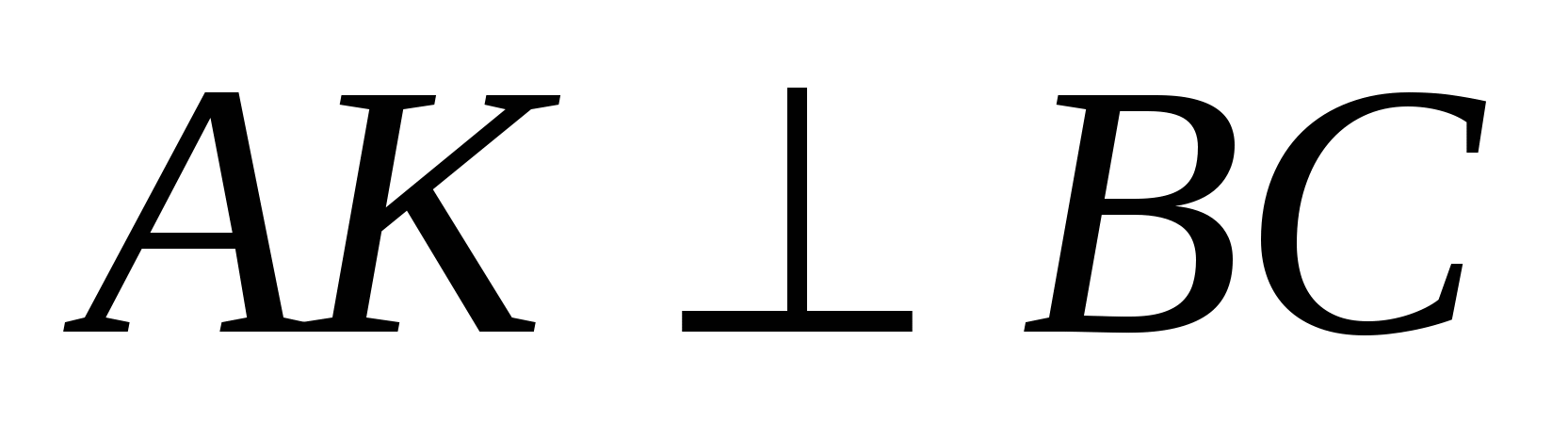 , то , то 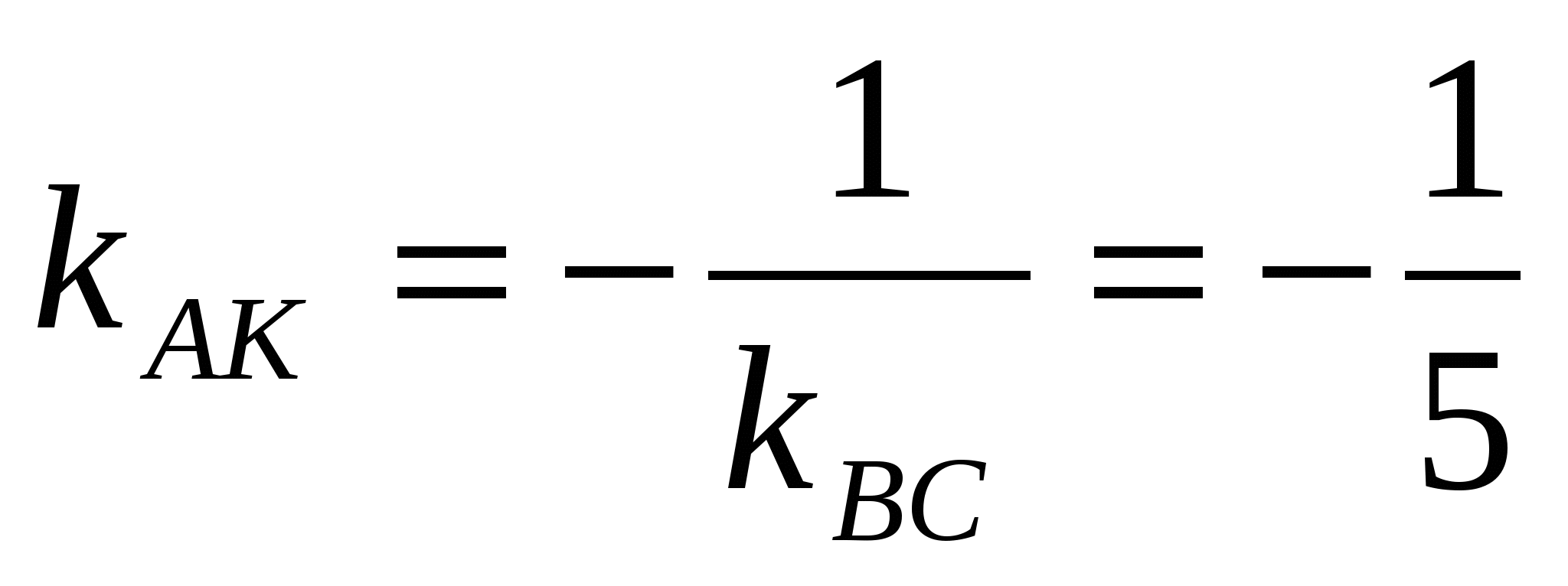
Уравнение 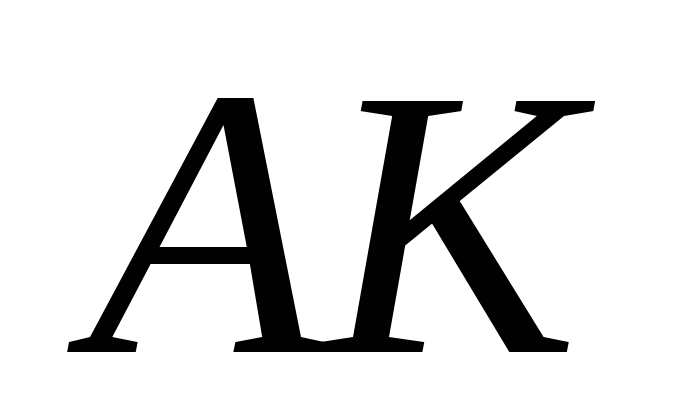 получим по формуле: получим по формуле:
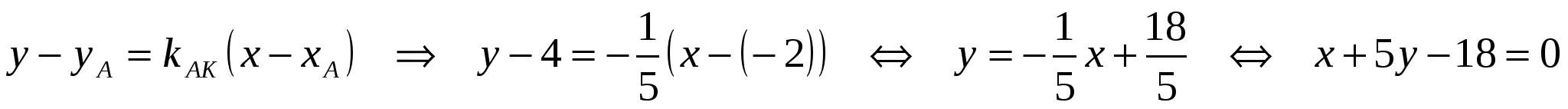 - уравнение - уравнение 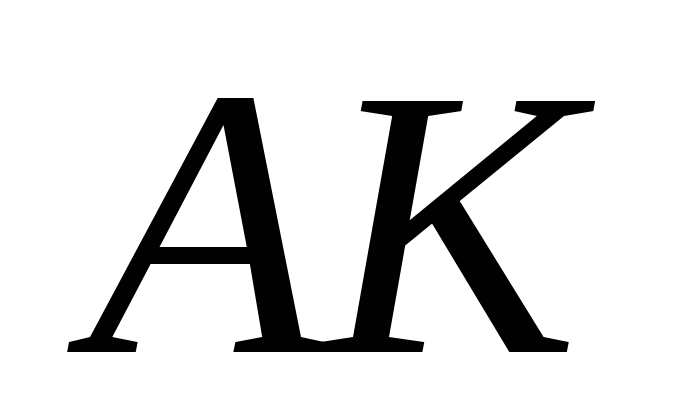
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если 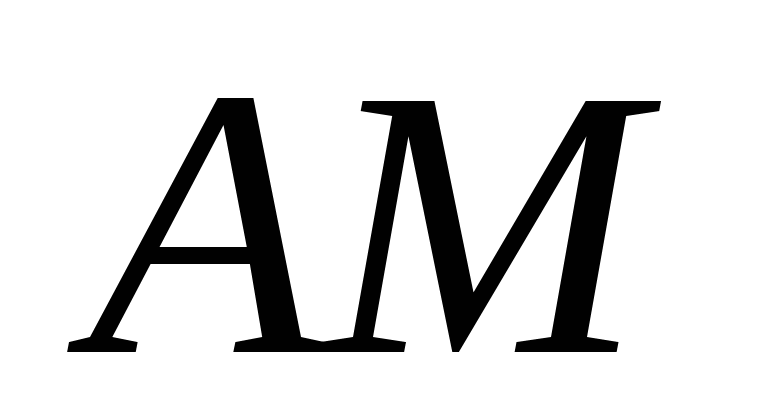 - медиана треугольника и - медиана треугольника и 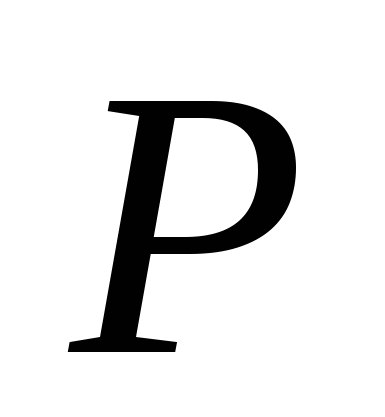 - точка пересечения медиан, то - точка пересечения медиан, то 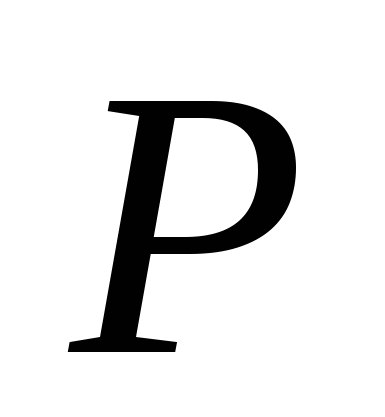 , делит , делит 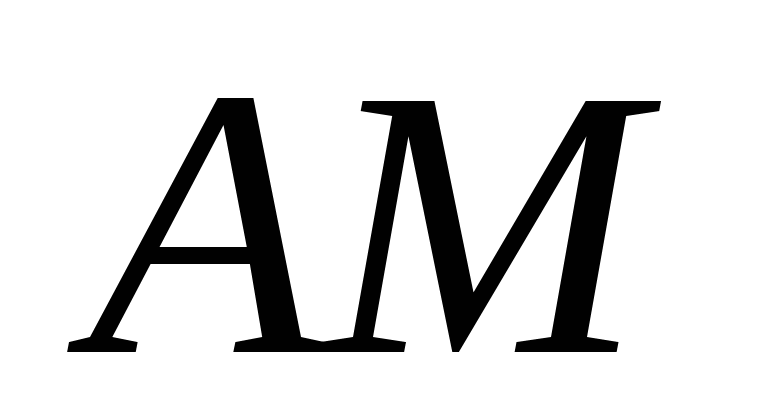 в отношении 2:1, начиная от точки в отношении 2:1, начиная от точки  , т.е. , т.е. 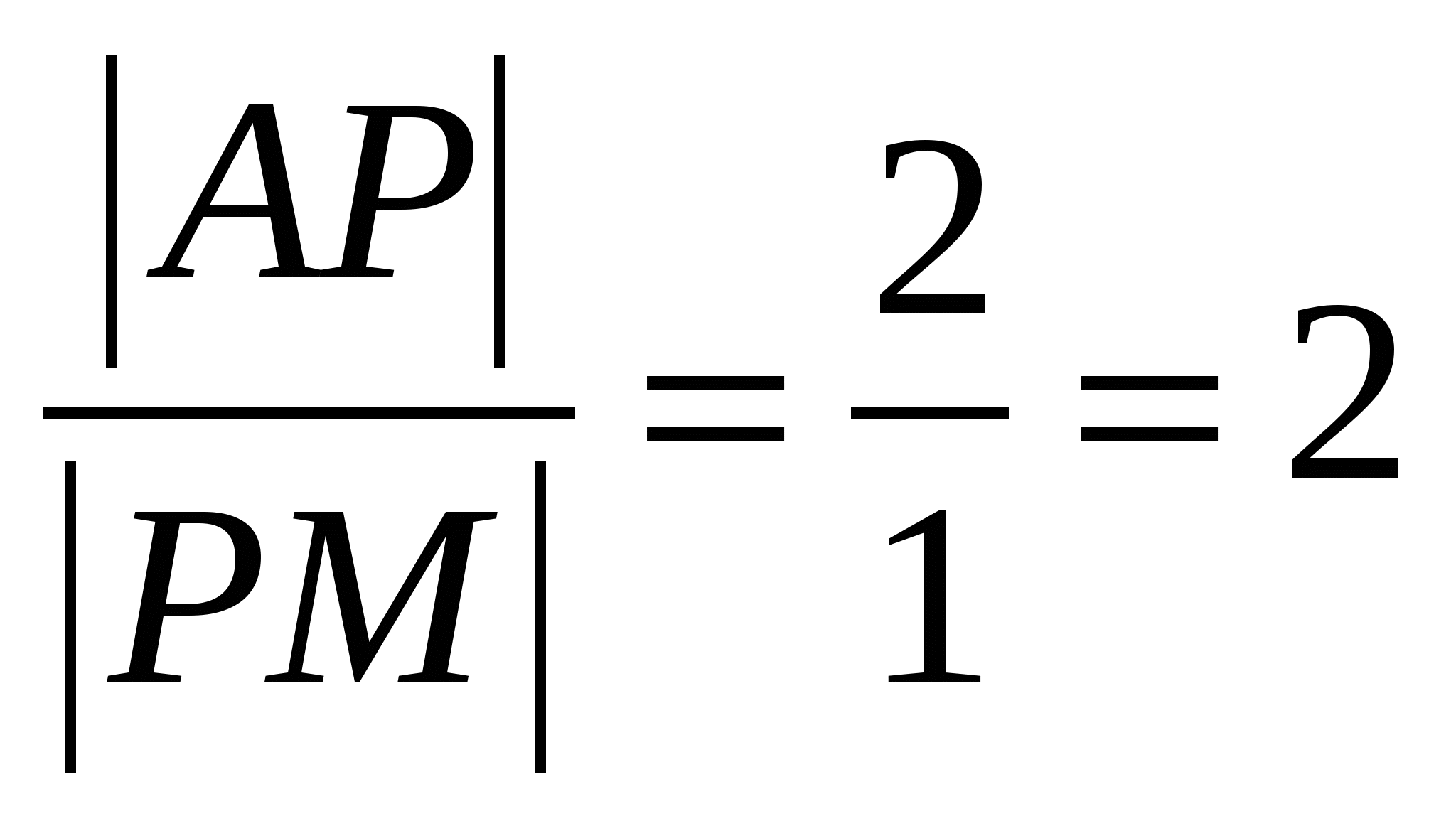
Основание медианы 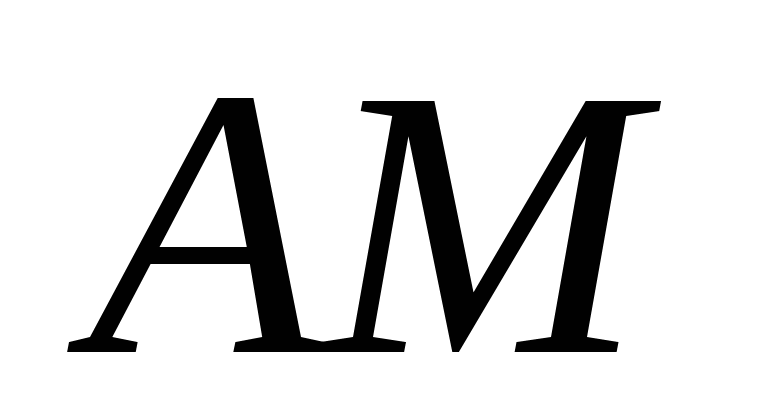 является серединой отрезка является серединой отрезка 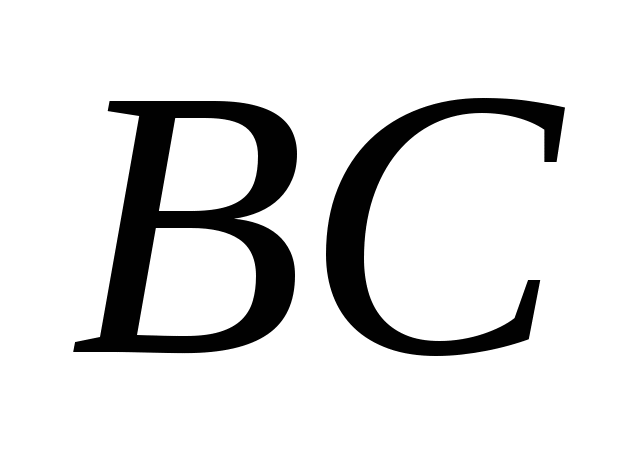 . Найдем координаты точки . Найдем координаты точки 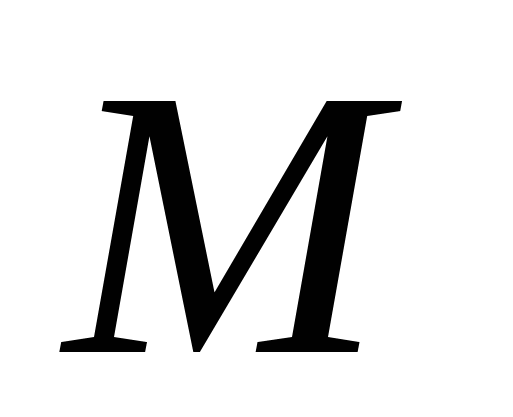 по формулам: по формулам:
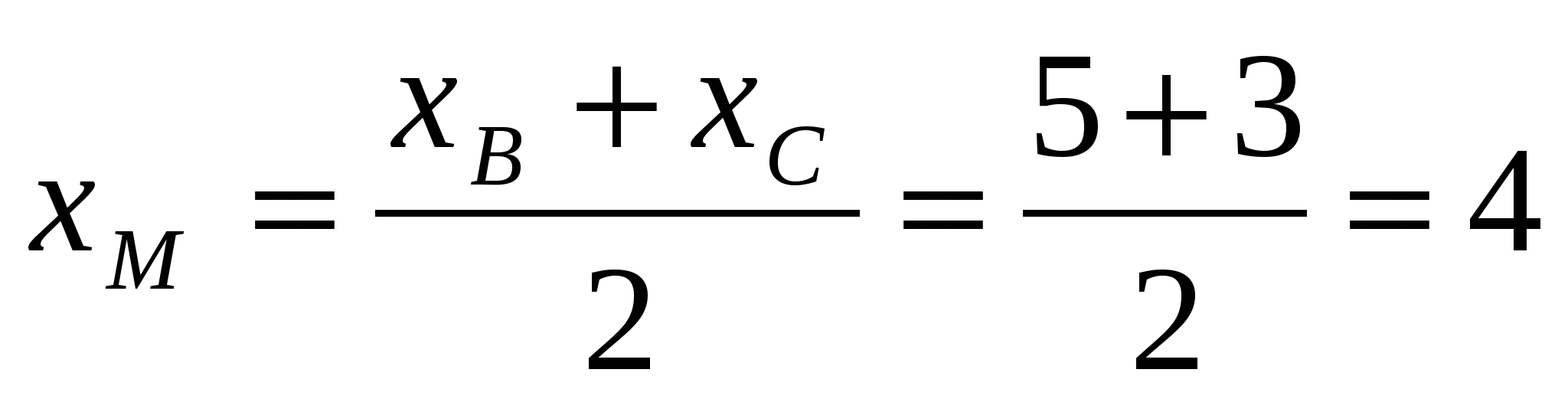 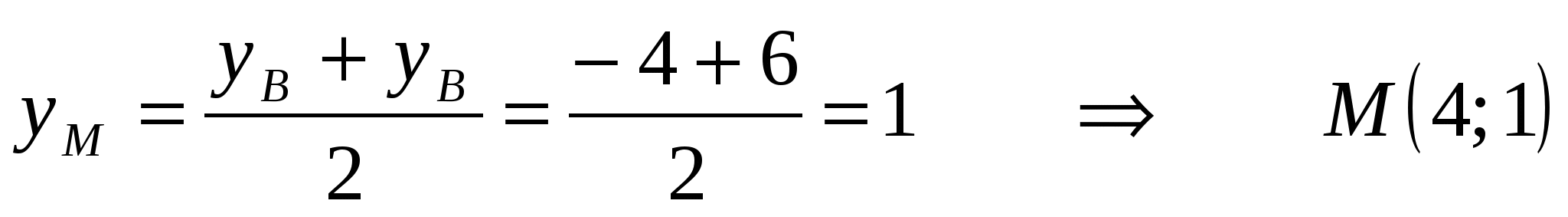
Теперь, когда координаты концов отрезка  известны, найдем координаты точки известны, найдем координаты точки  , которая делит , которая делит 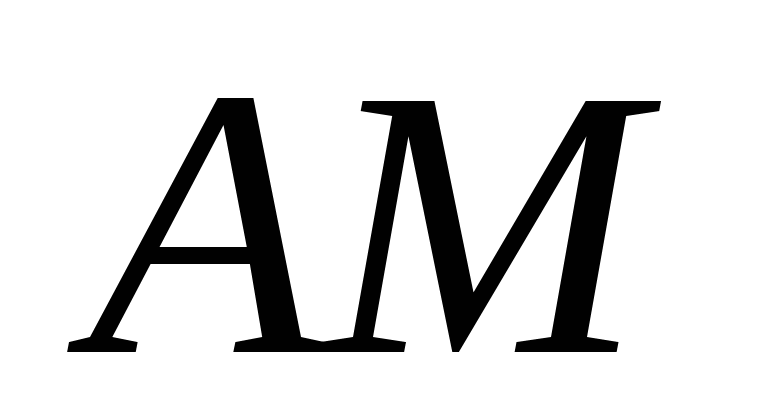 в отношении в отношении 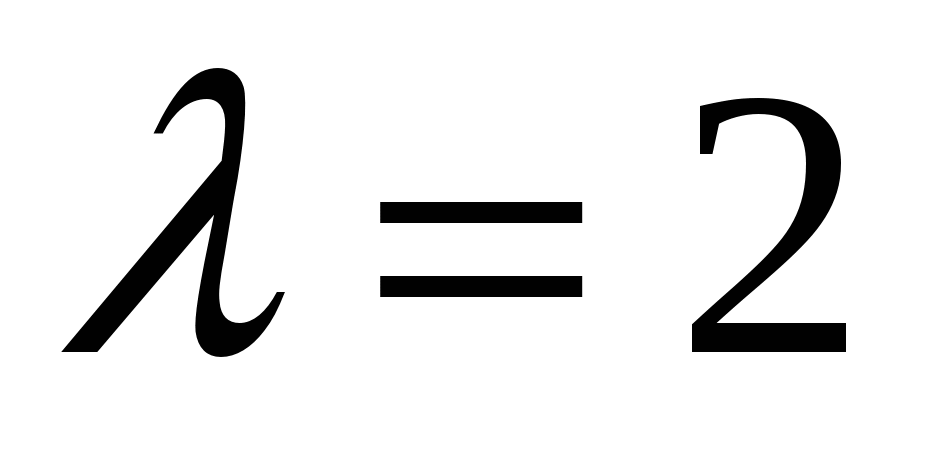 , начиная от точки , начиная от точки  , по формулам деления отрезка в заданном соотношении: , по формулам деления отрезка в заданном соотношении:
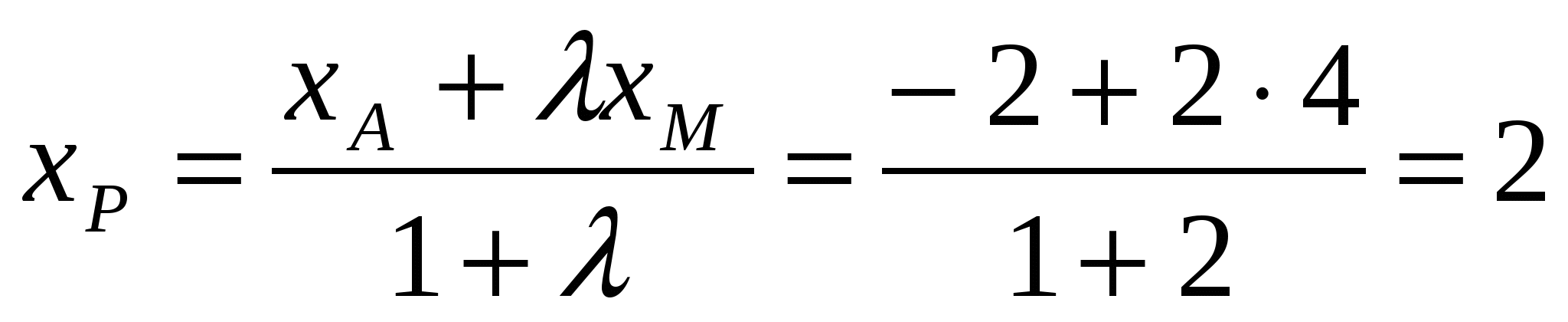 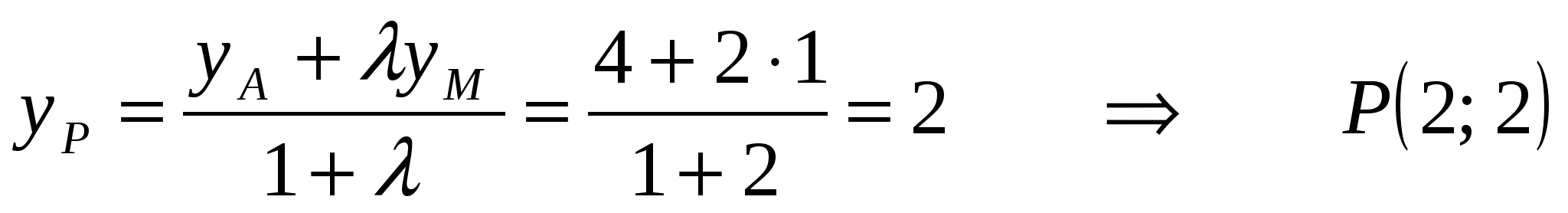 - центр тяжести треугольника - центр тяжести треугольника 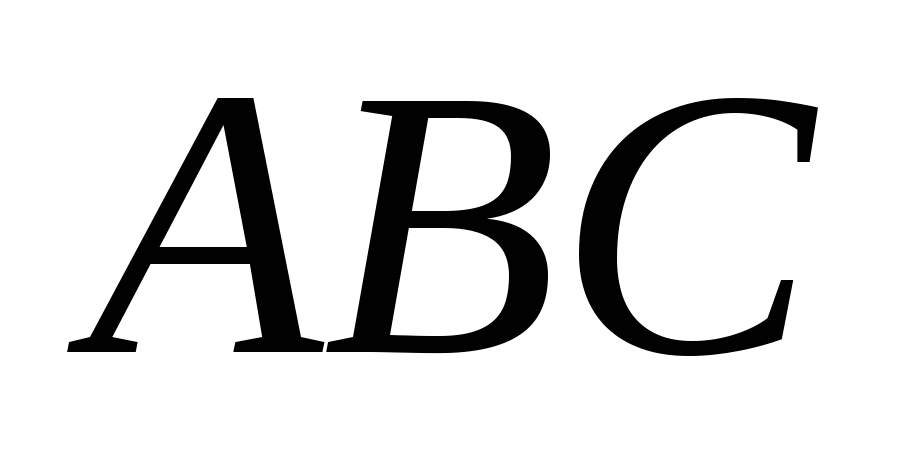 . .
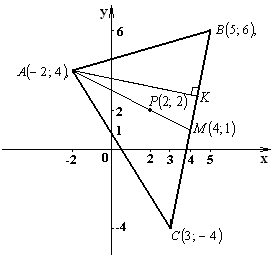
6) Построим чертеж к задаче в системе координат 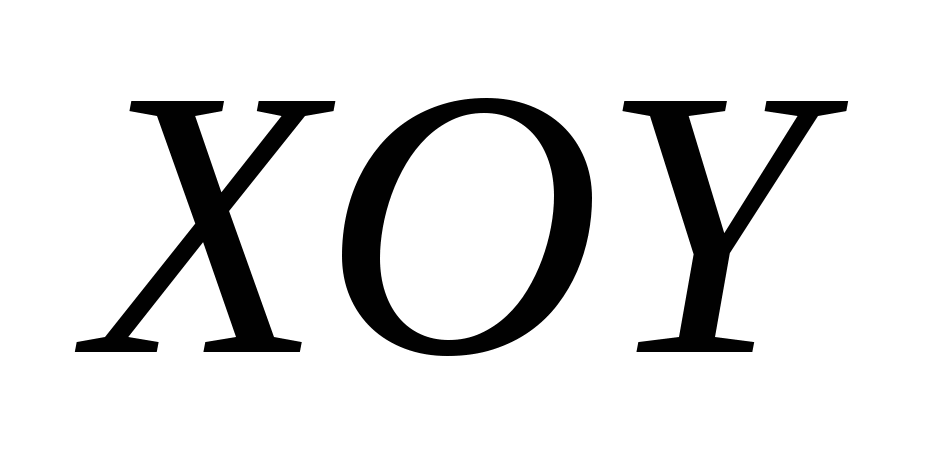 . Полученные при решении задачи результаты не противоречат чертежу. . Полученные при решении задачи результаты не противоречат чертежу.
Ответы:
длина стороны 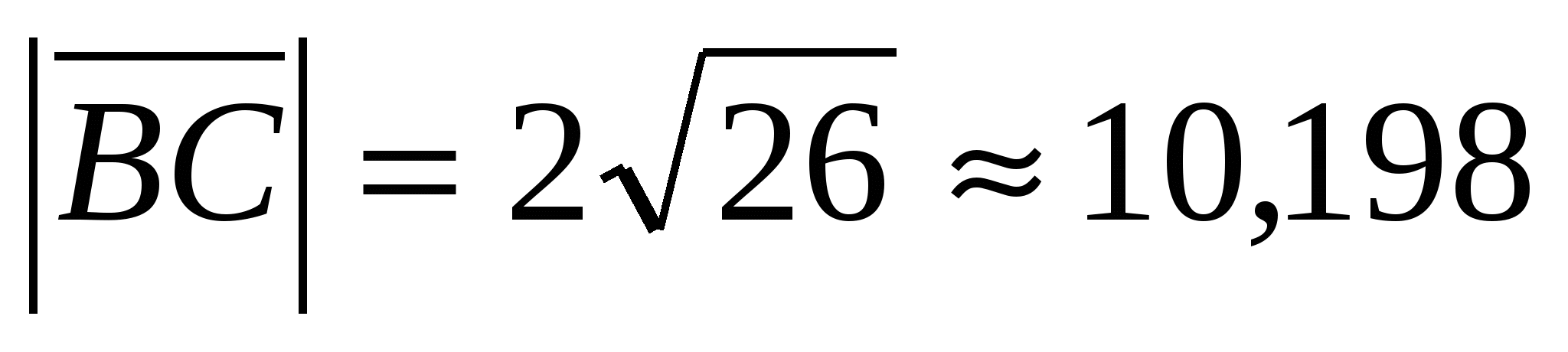 ; ;
уравнение стороны 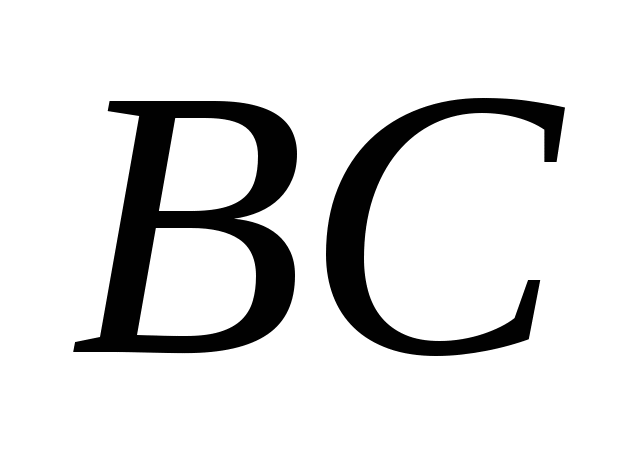 : : 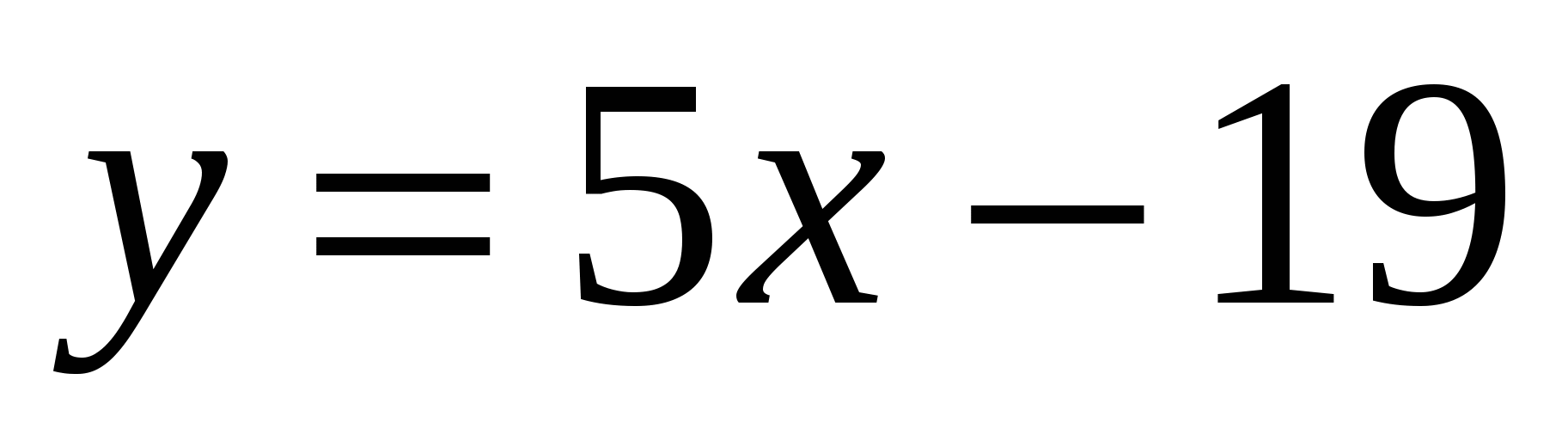 ; ;
угол при вершине 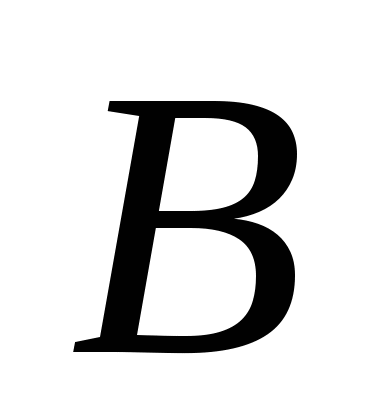 : : 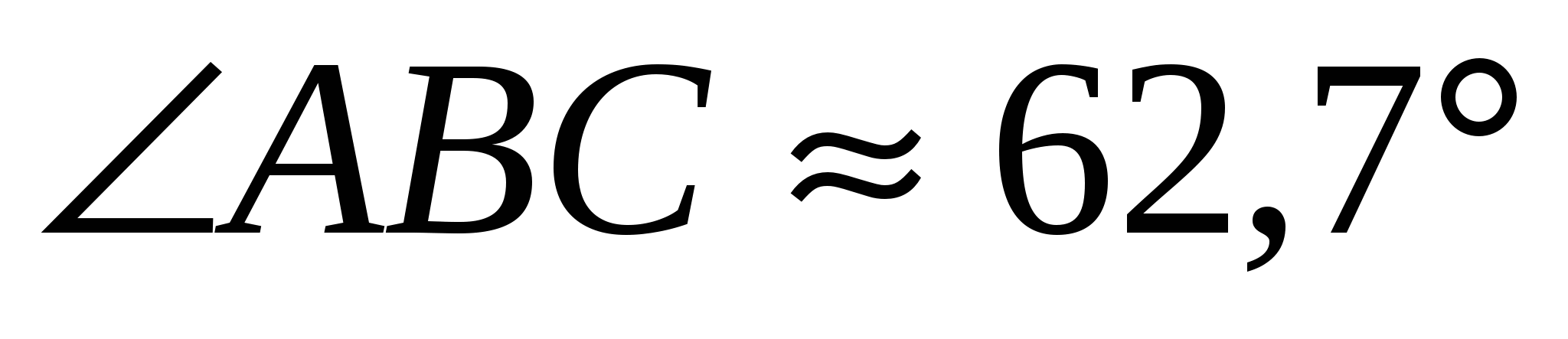 ; ;
уравнение высоты 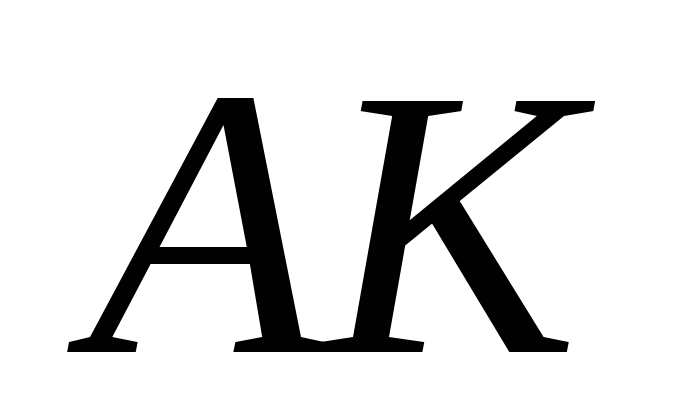 : : 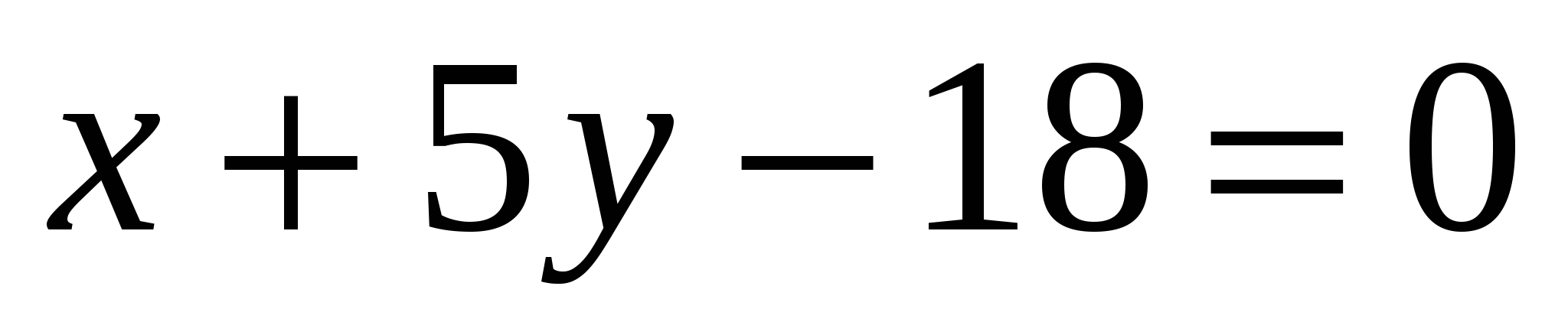 ; ;
координаты центра тяжести треугольника: 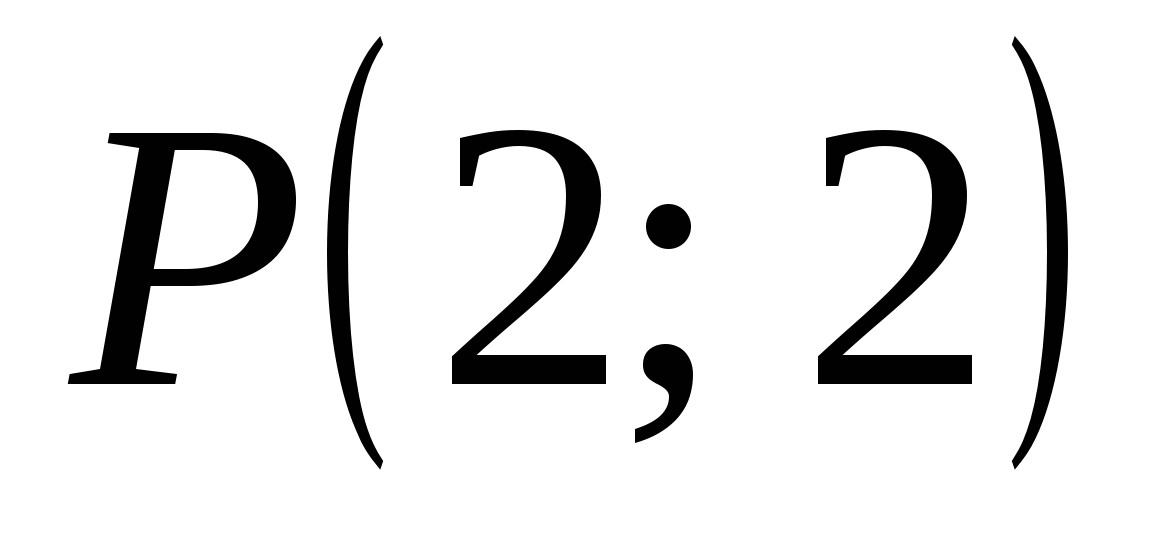 . .
Задача 2. Даны координаты точки 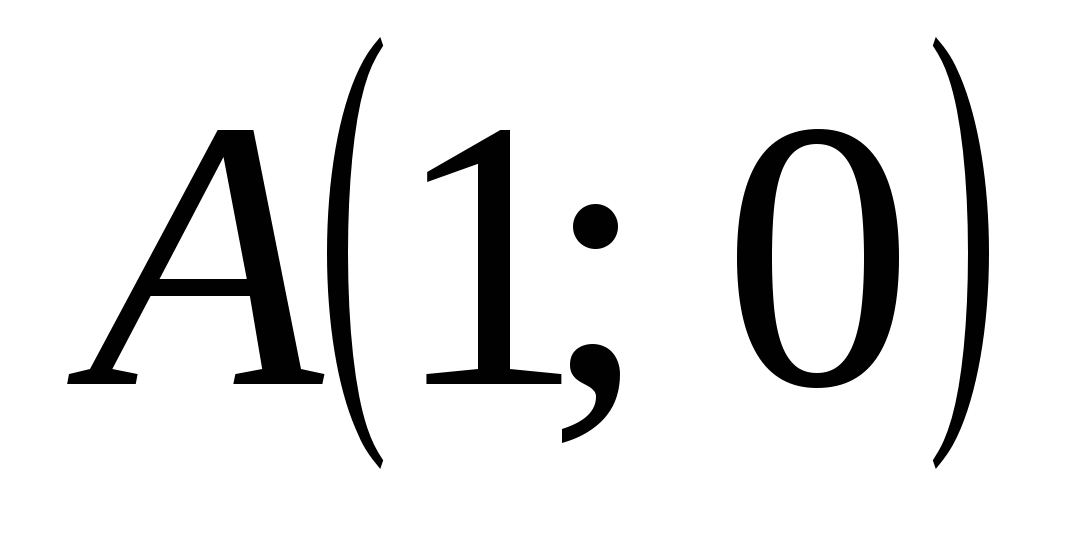 , уравнение прямой , уравнение прямой 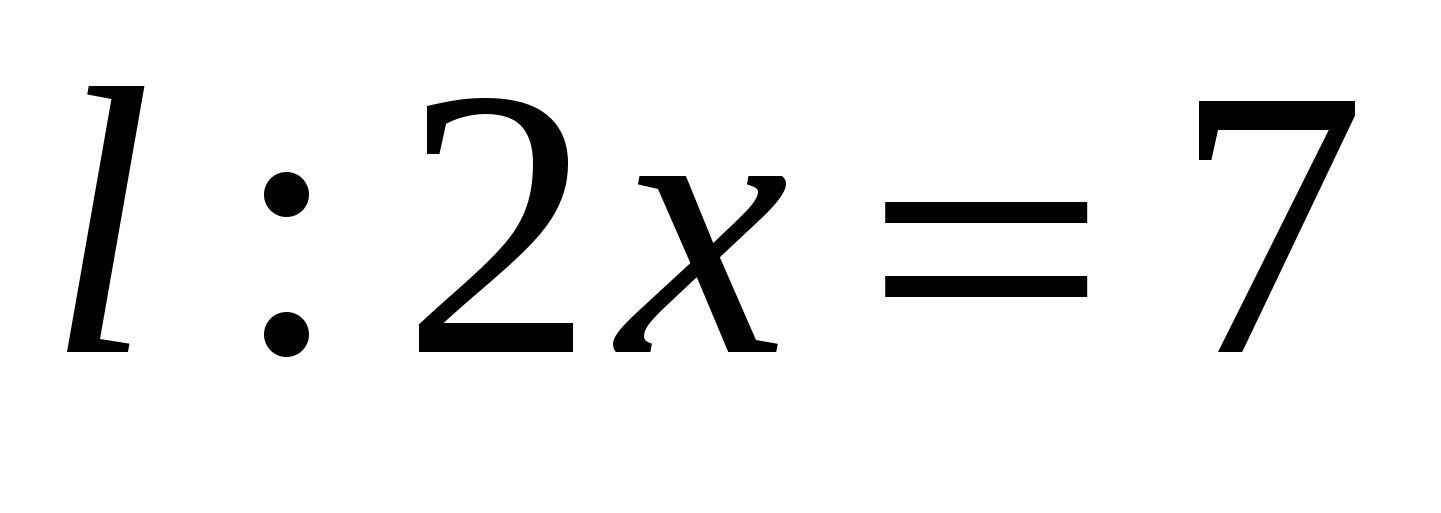 и число и число 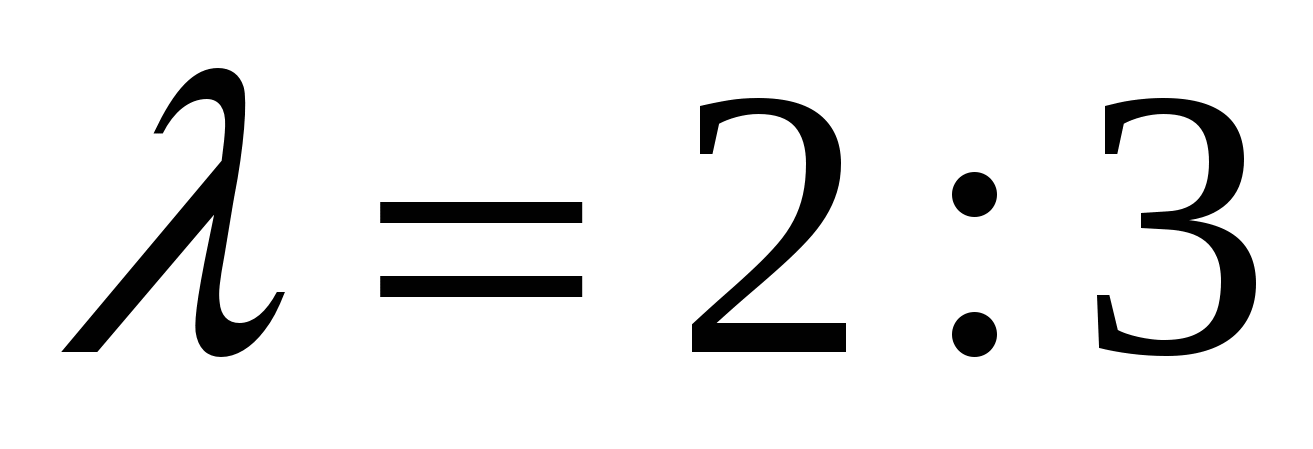 . Найти траекторию точки . Найти траекторию точки 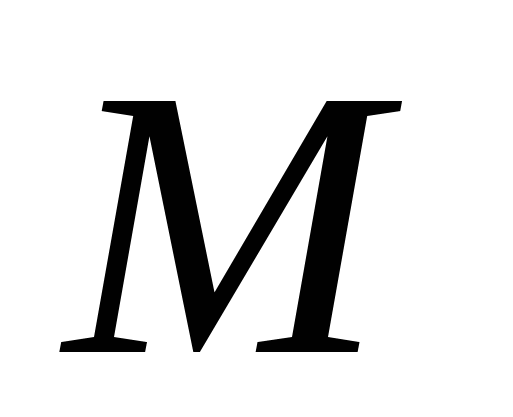 , которая движется в плоскости так, что отношение ее расстояния до точки А и до прямой , которая движется в плоскости так, что отношение ее расстояния до точки А и до прямой 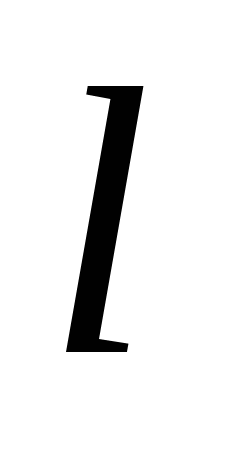 равно равно 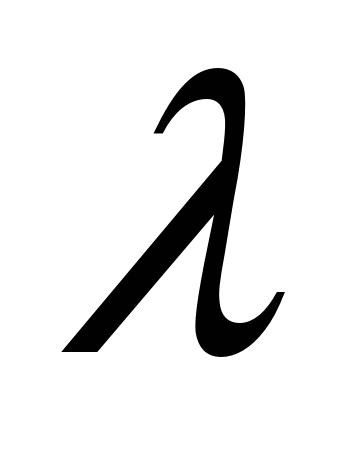 . Сделать чертеж в системе координат. . Сделать чертеж в системе координат.
Решение
Пусть 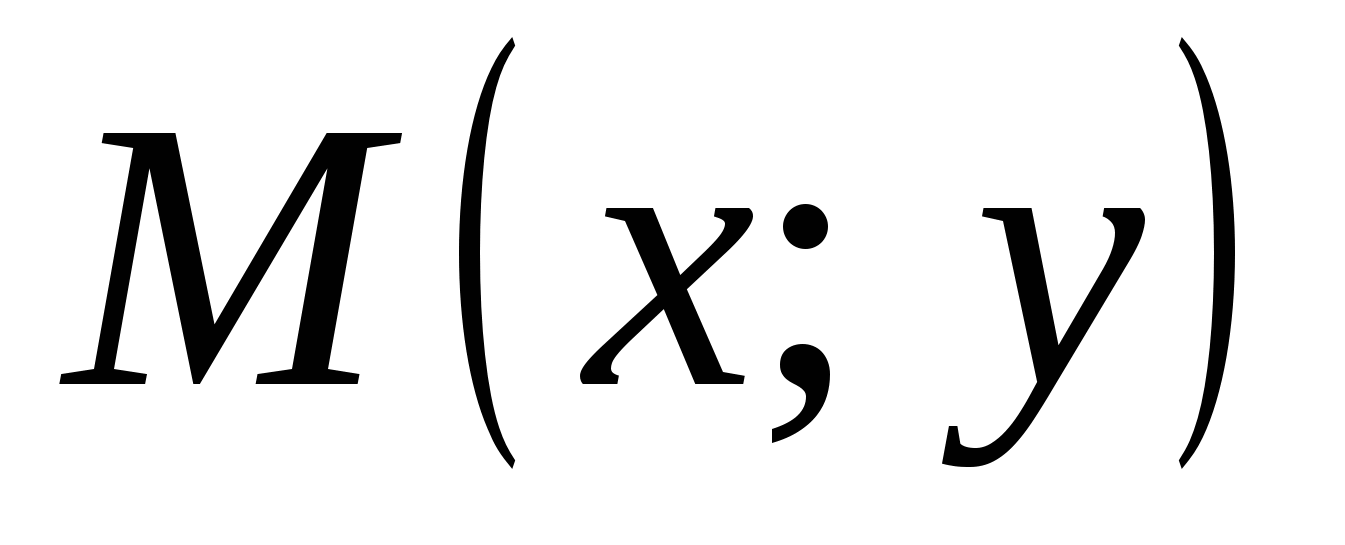 - произвольная точка на координатной плоскости, удовлетворяющая условию задачи, т.е. - произвольная точка на координатной плоскости, удовлетворяющая условию задачи, т.е. 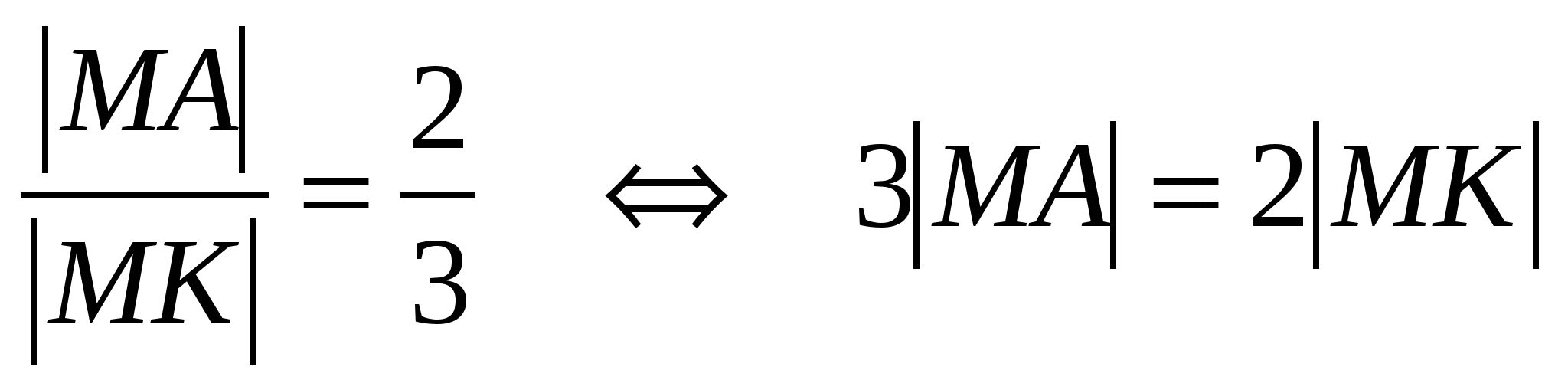 , где , где 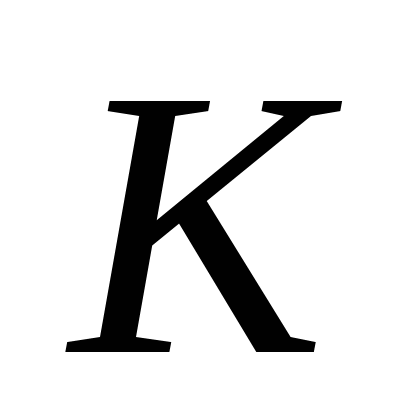 - основание перпендикуляра, опущенного из точки - основание перпендикуляра, опущенного из точки 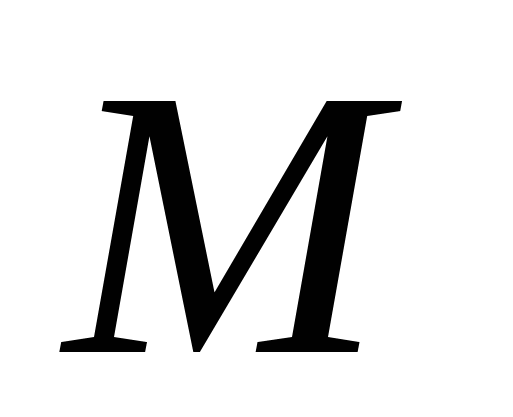 на прямую на прямую 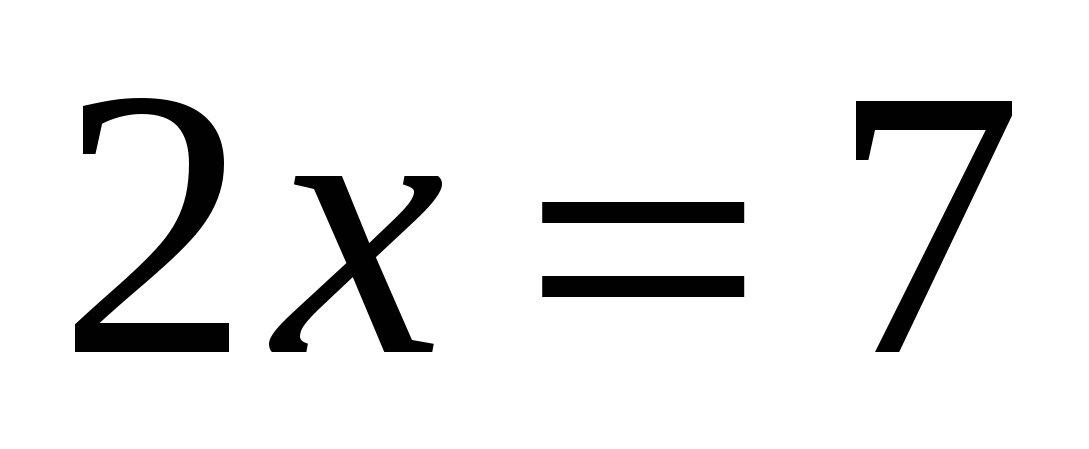 . Так как . Так как 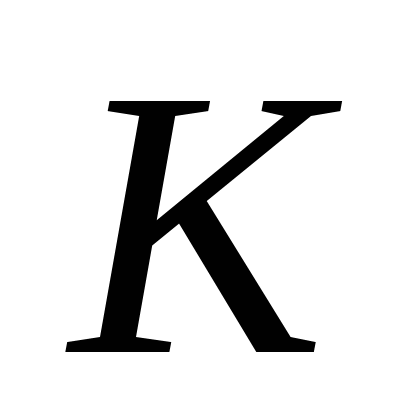 лежит на прямой лежит на прямой 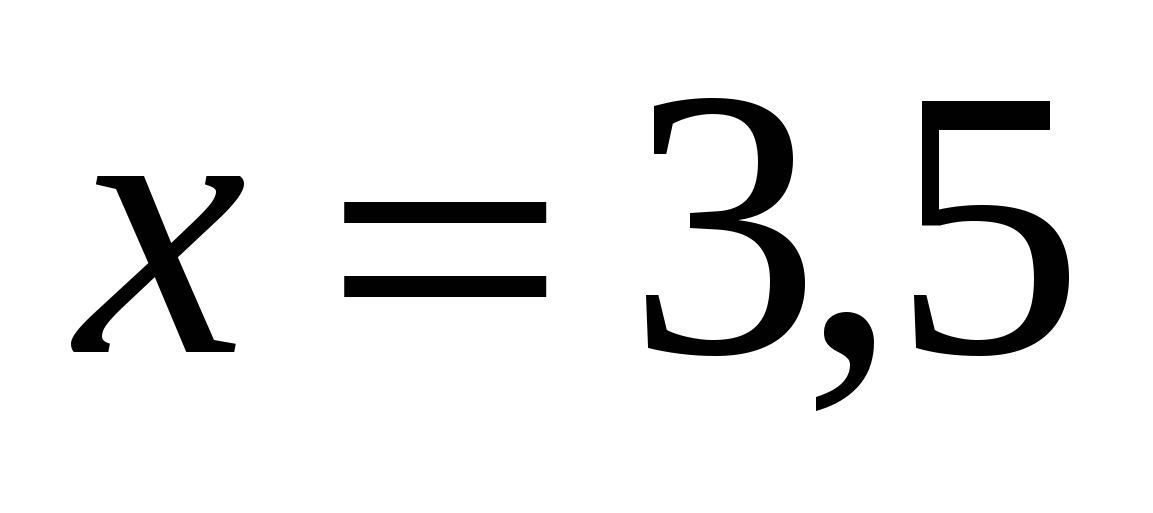 , то , то 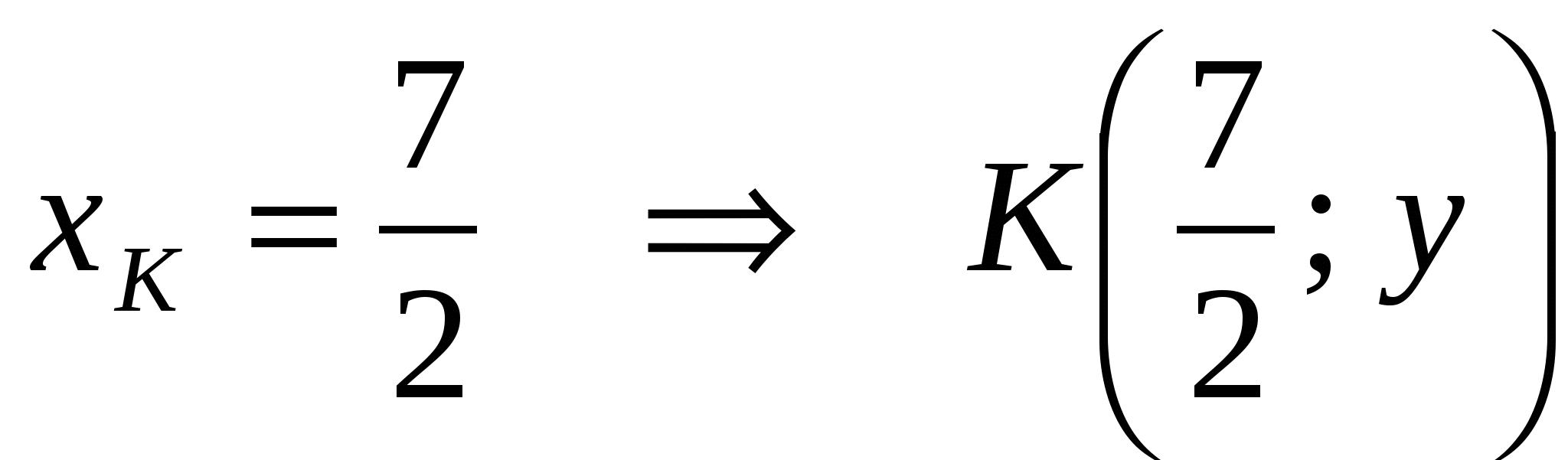 . .
Запишем условие 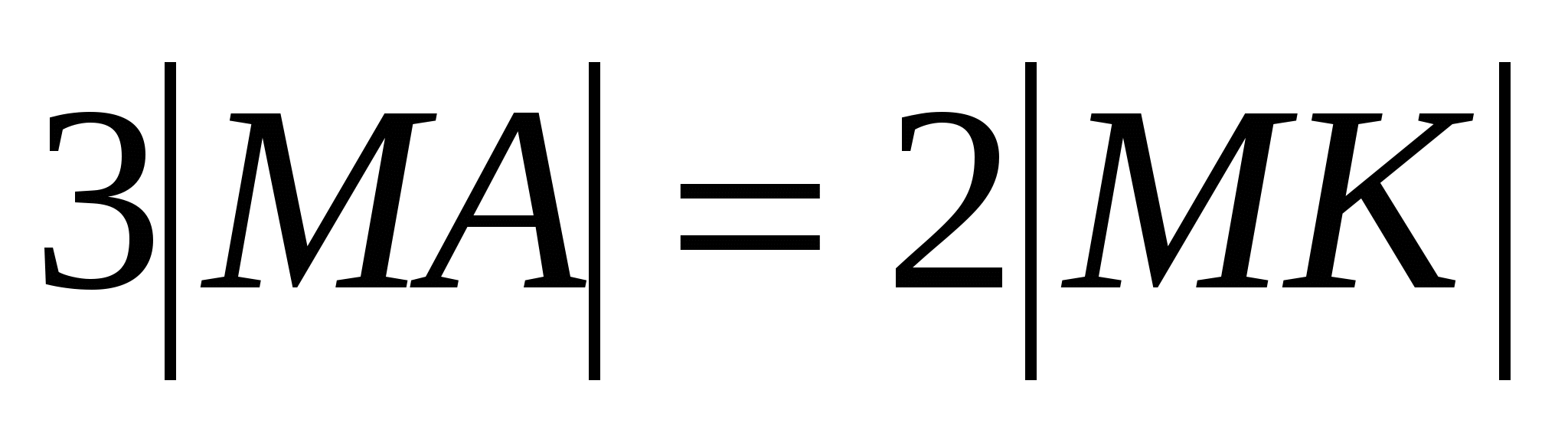 в координатной форме, используя формулу для длины отрезка: в координатной форме, используя формулу для длины отрезка:
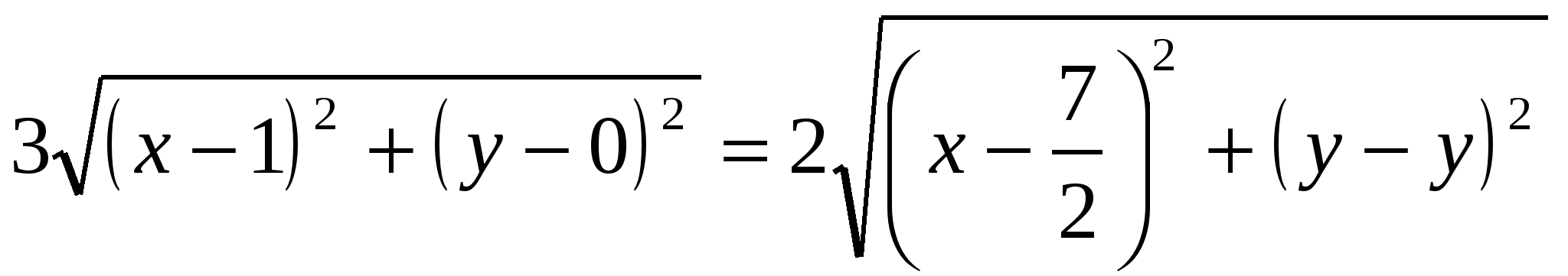
Это и есть уравнение искомой траектории, т.к. ему удовлетворяют координаты любой точки 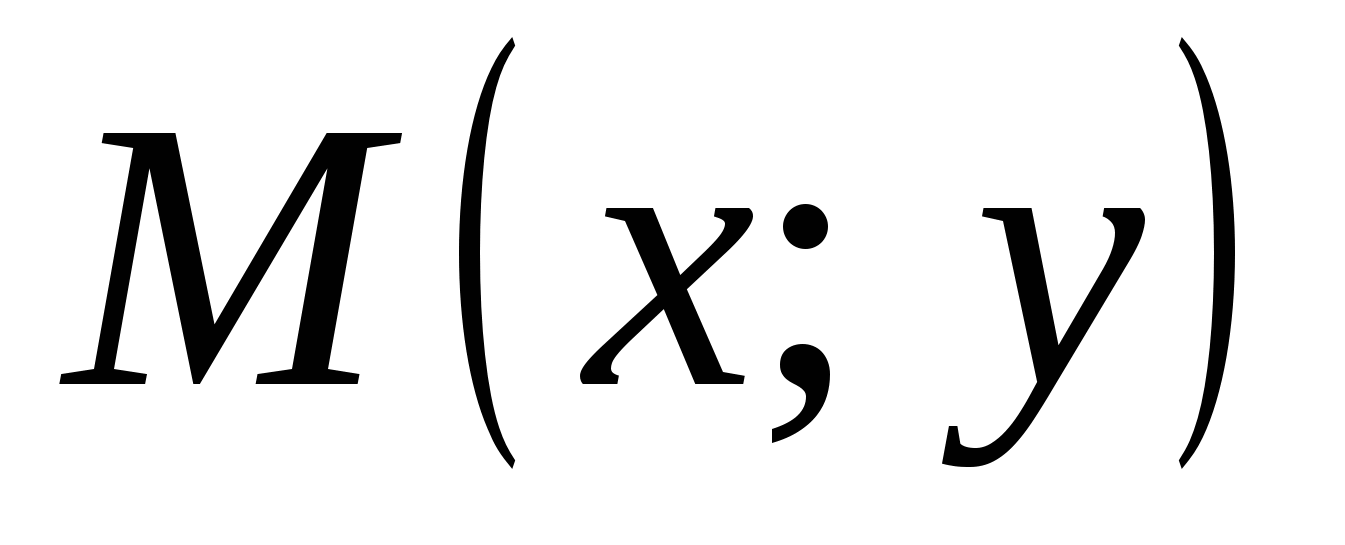 на этой траектории. на этой траектории.
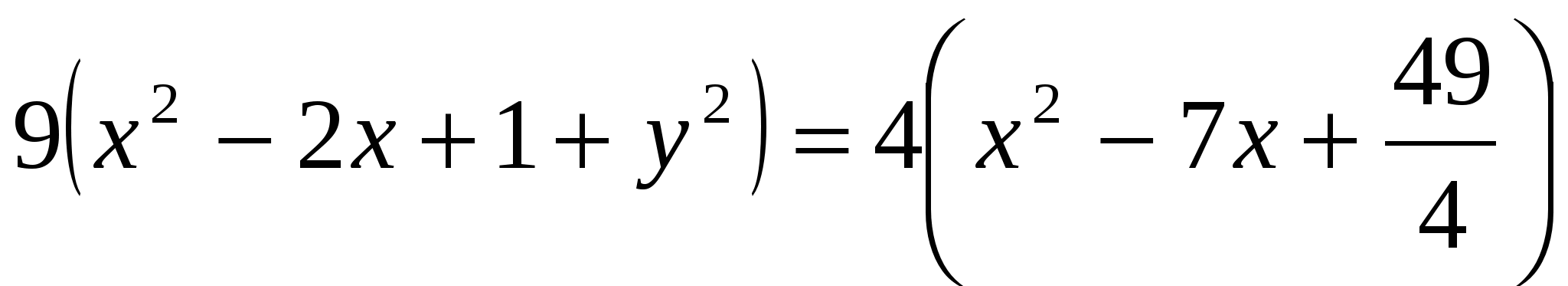
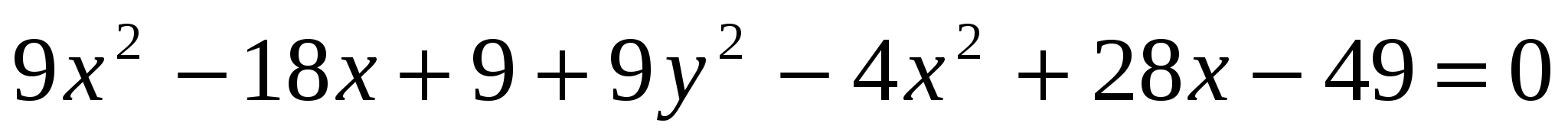
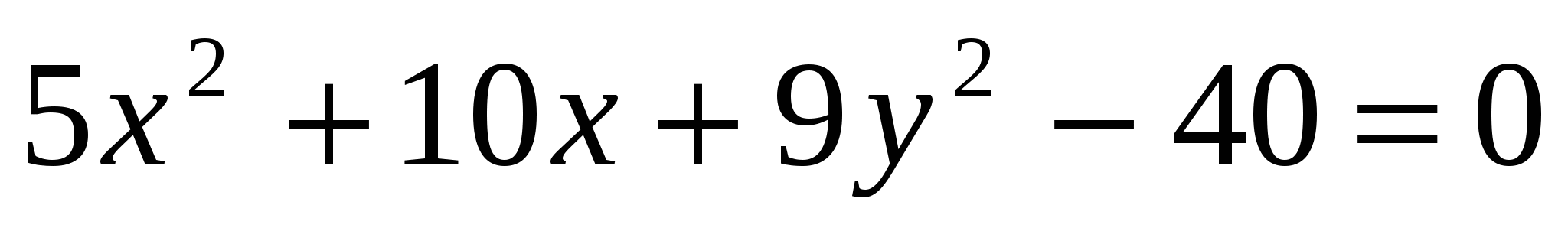
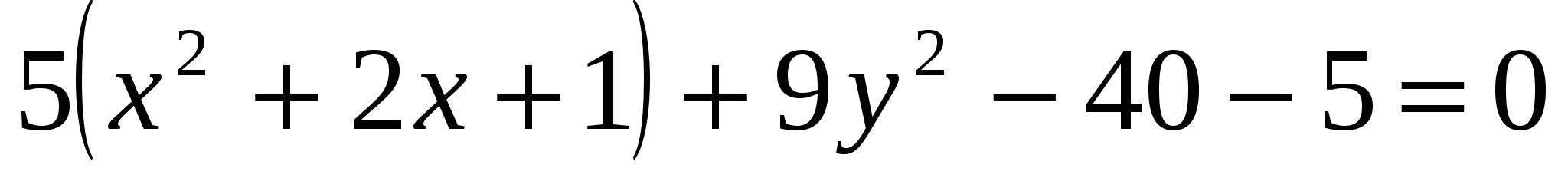
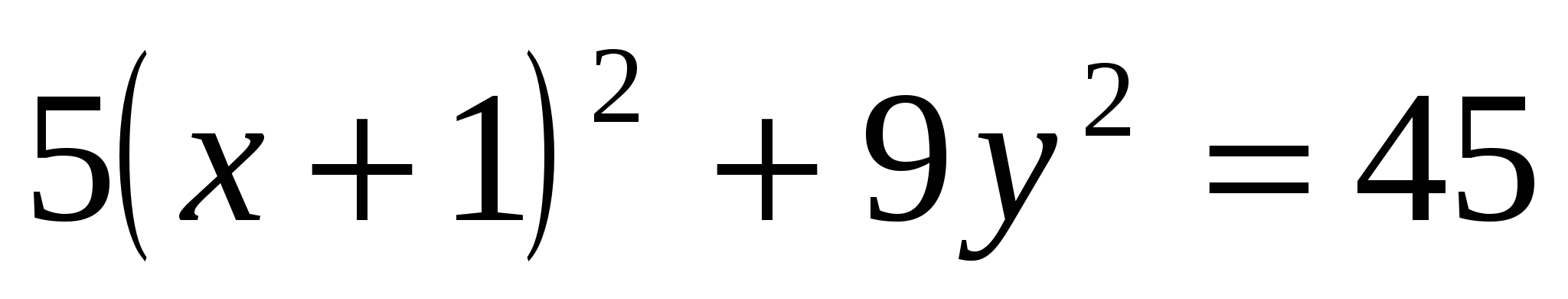
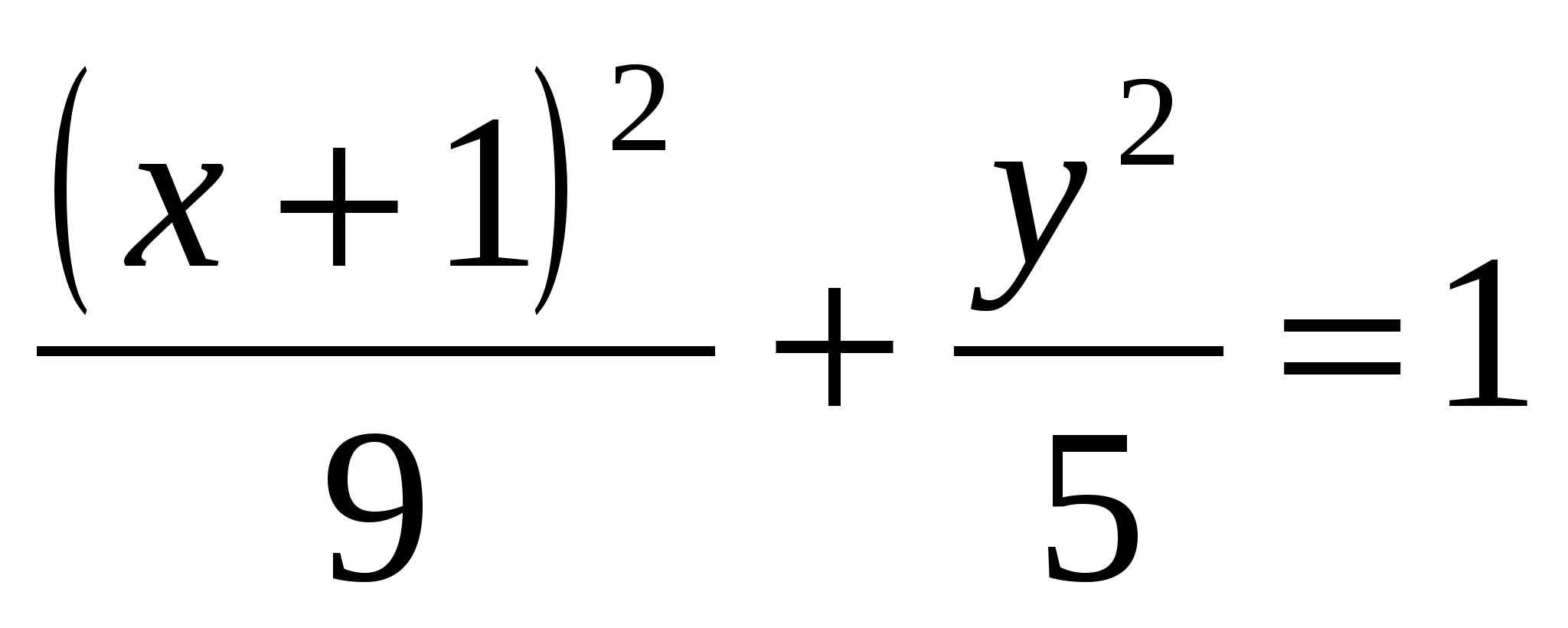
- уравнение эллипса с полуосями 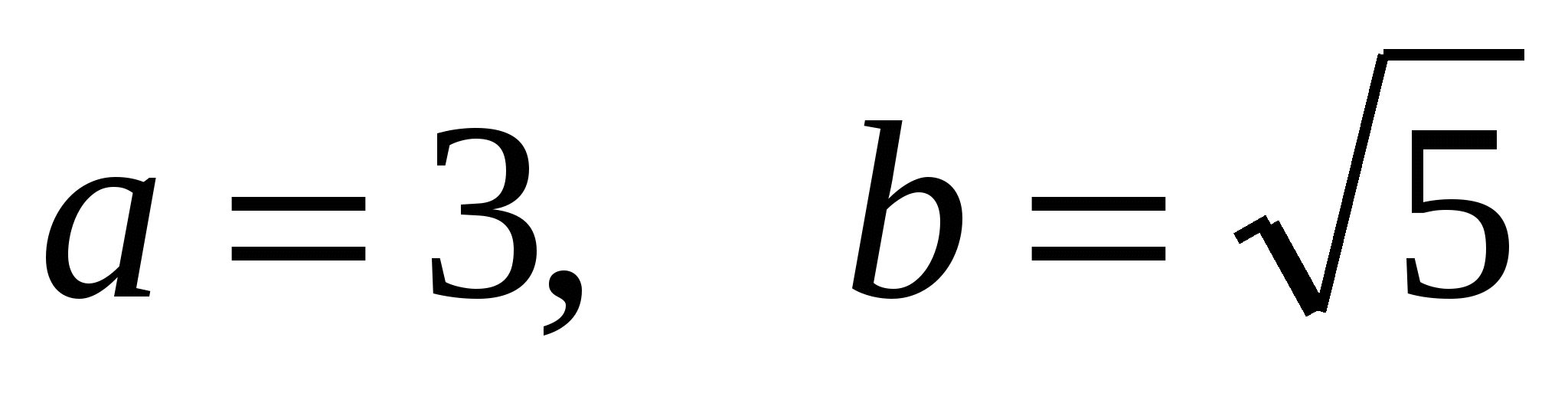 . Центр эллипса – точка . Центр эллипса – точка 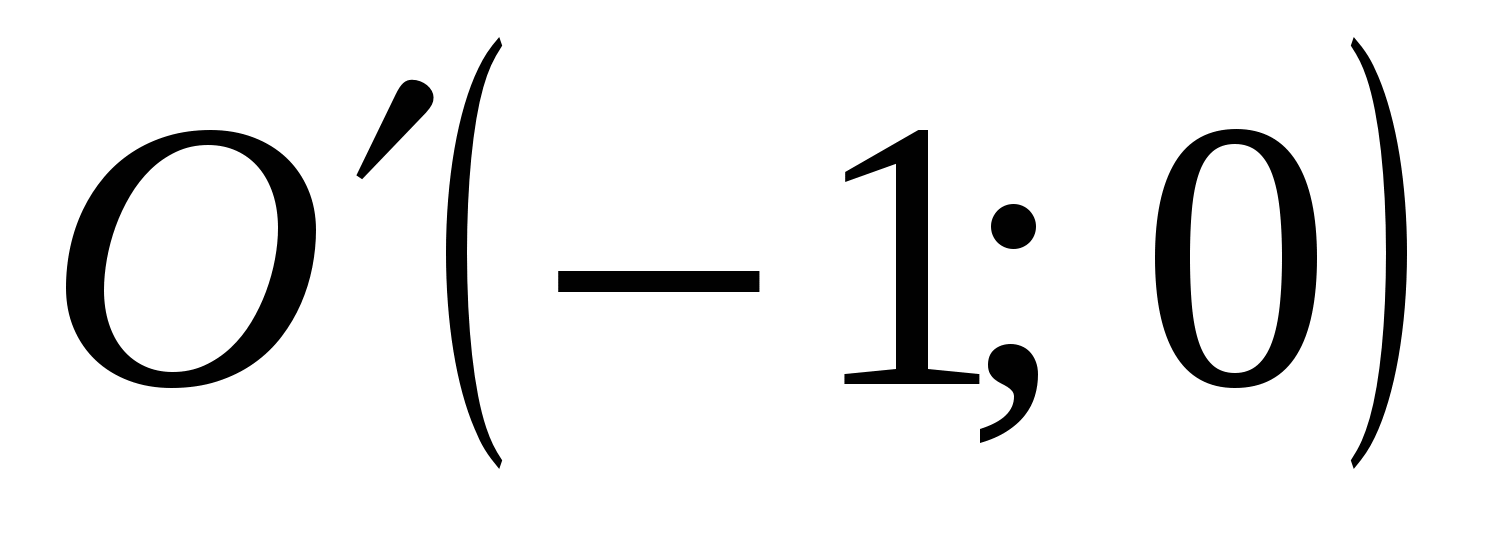 . .
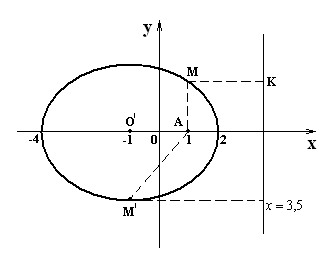
Ответ: 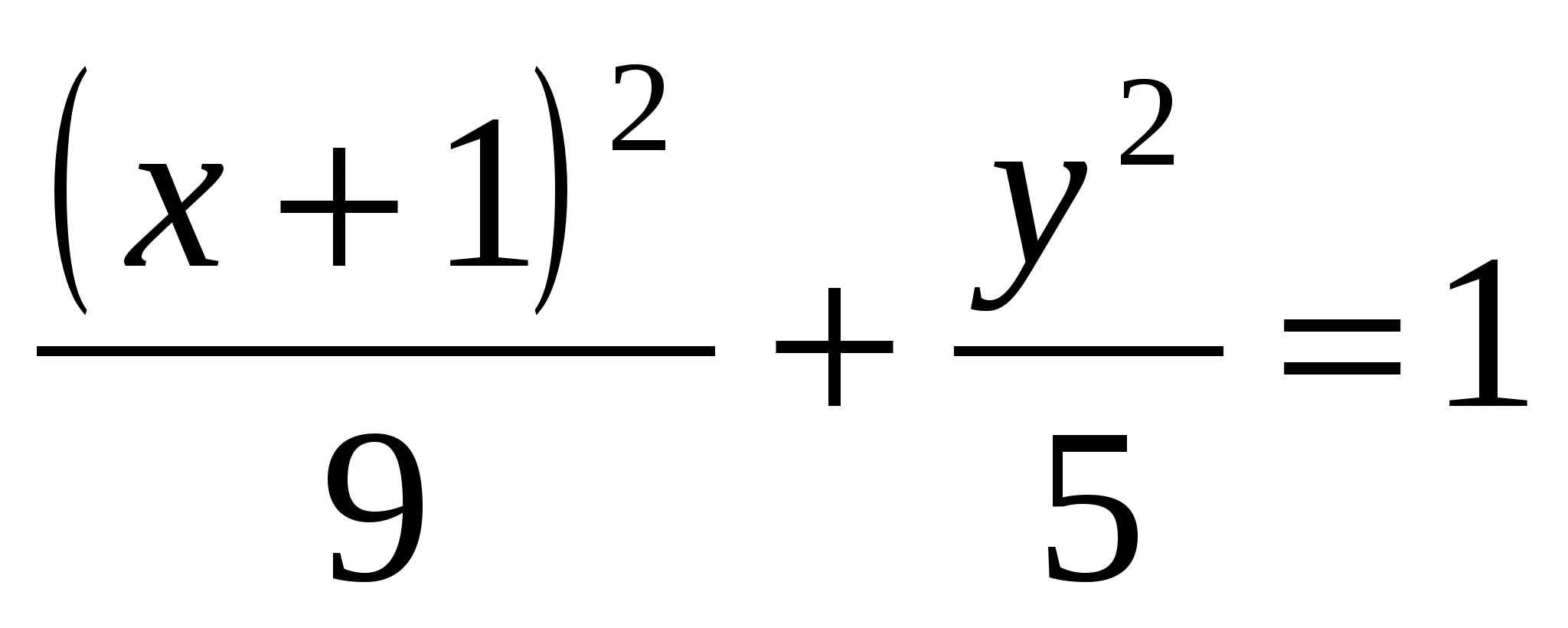 - уравнение траектории. - уравнение траектории.
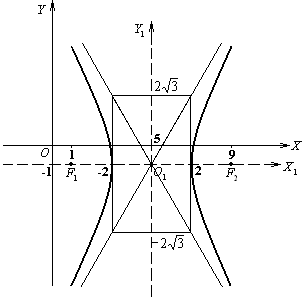
Задача 3. Дано уравнение второго порядка 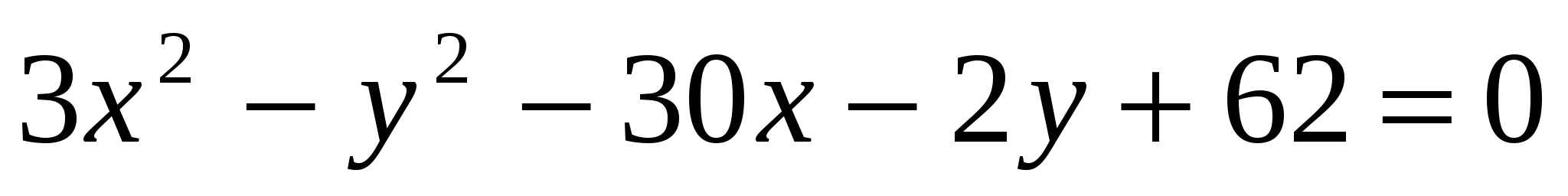 . Привести данное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение исходной кривой относительно обеих систем координат. . Привести данное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение исходной кривой относительно обеих систем координат.
Решение
Выделим в уравнении полные квадраты по переменным 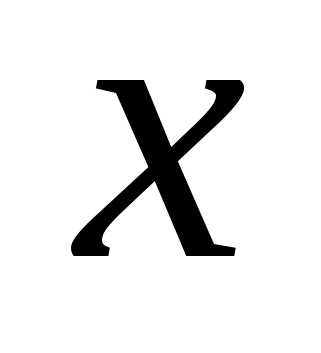 и и 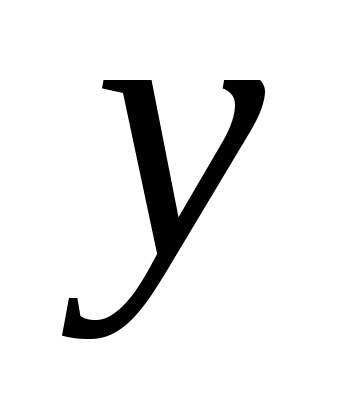 . .
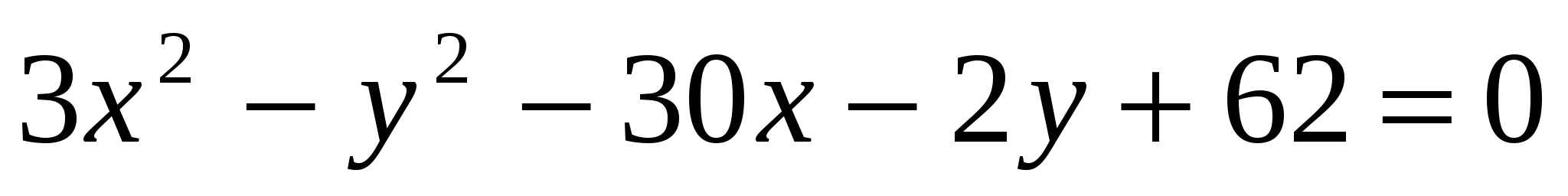
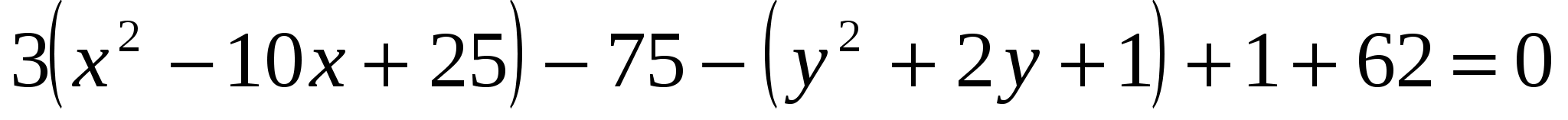
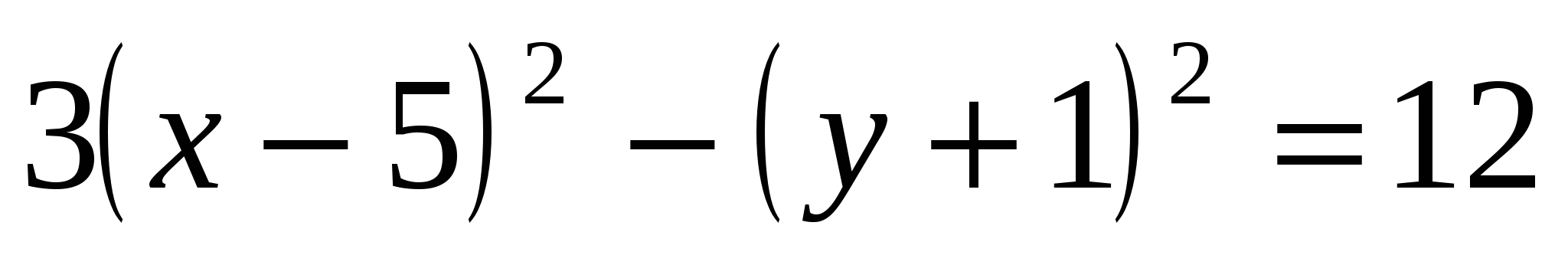
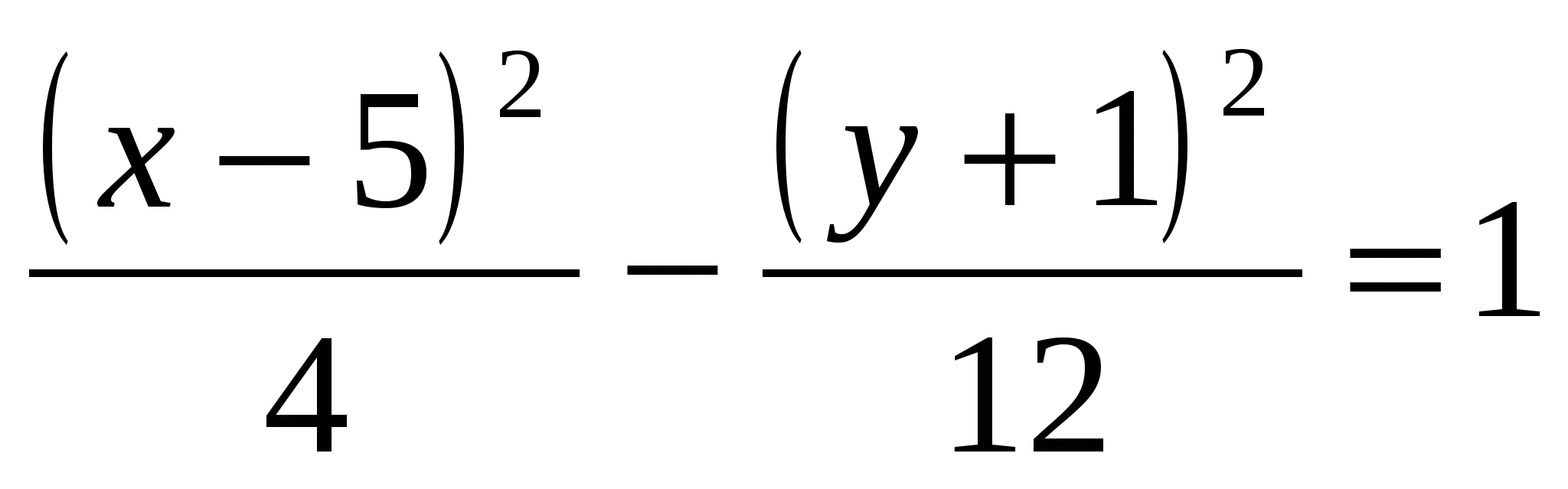
Получили уравнение гиперболы с центром в точке 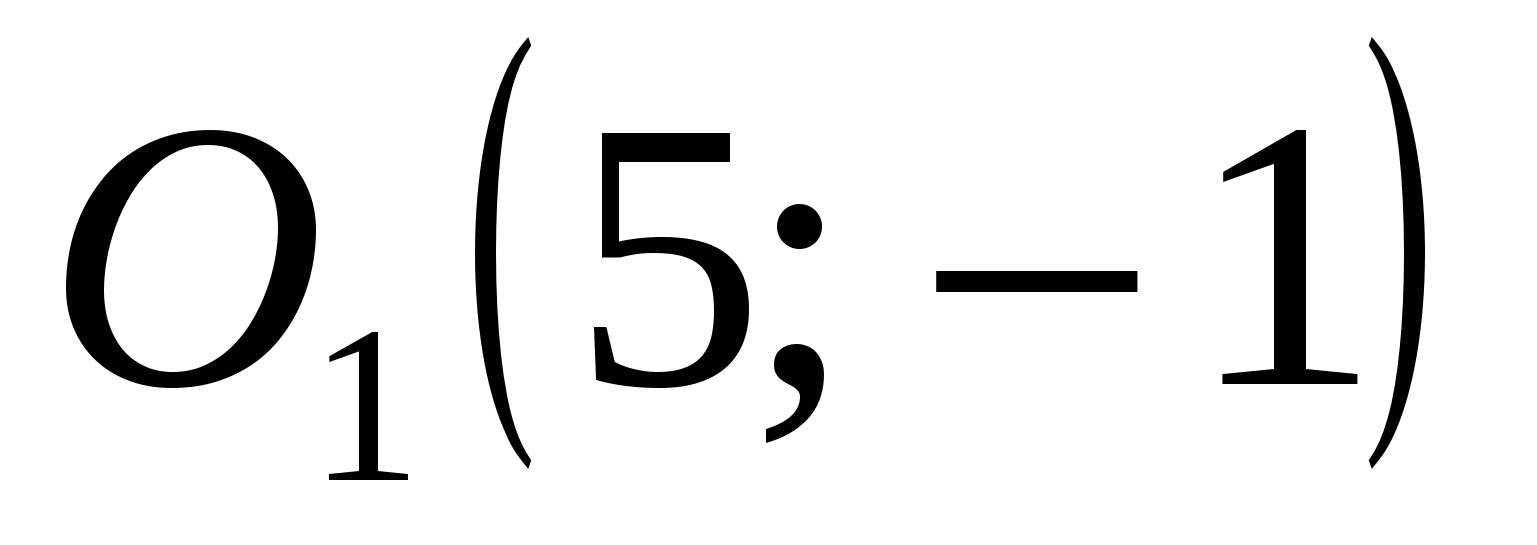 . .
Осуществив параллельный перенос осей координат в системе 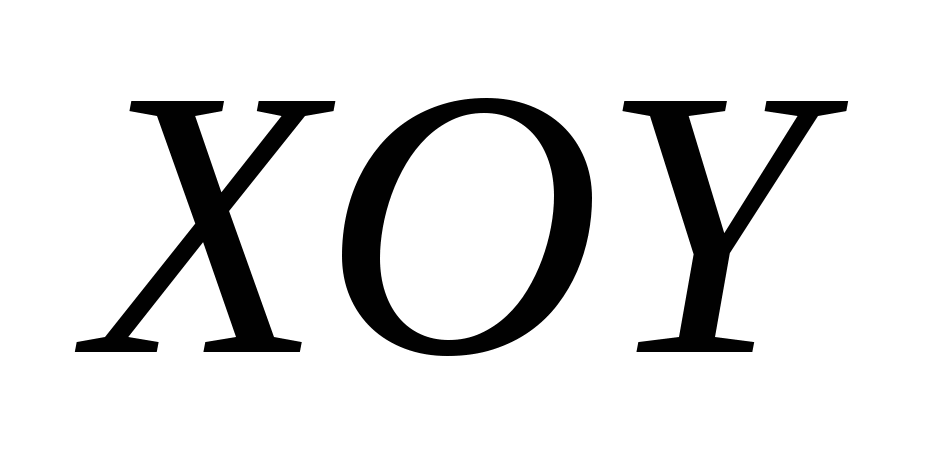 по формулам по формулам 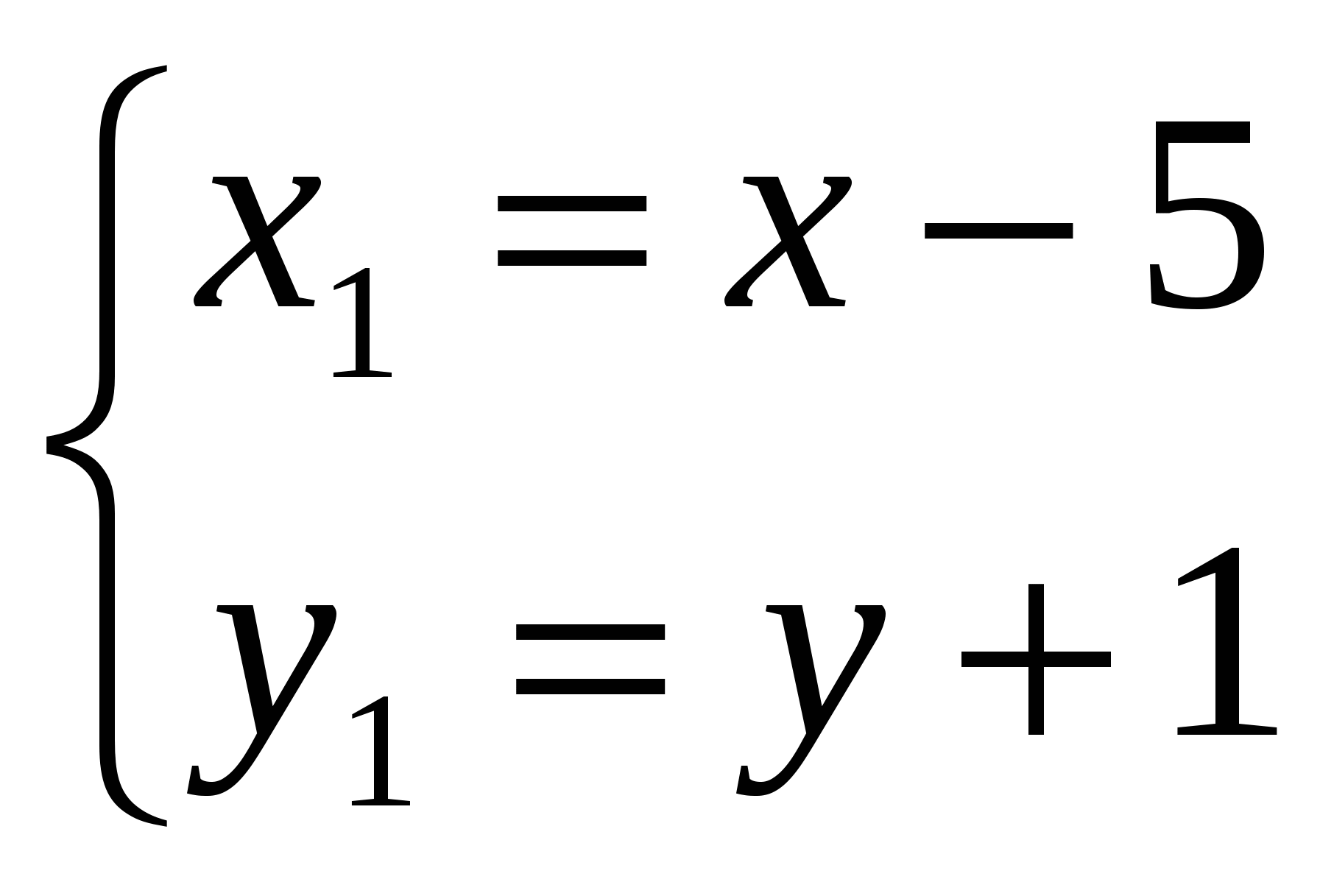 , получим каноническое уравнение гиперболы , получим каноническое уравнение гиперболы 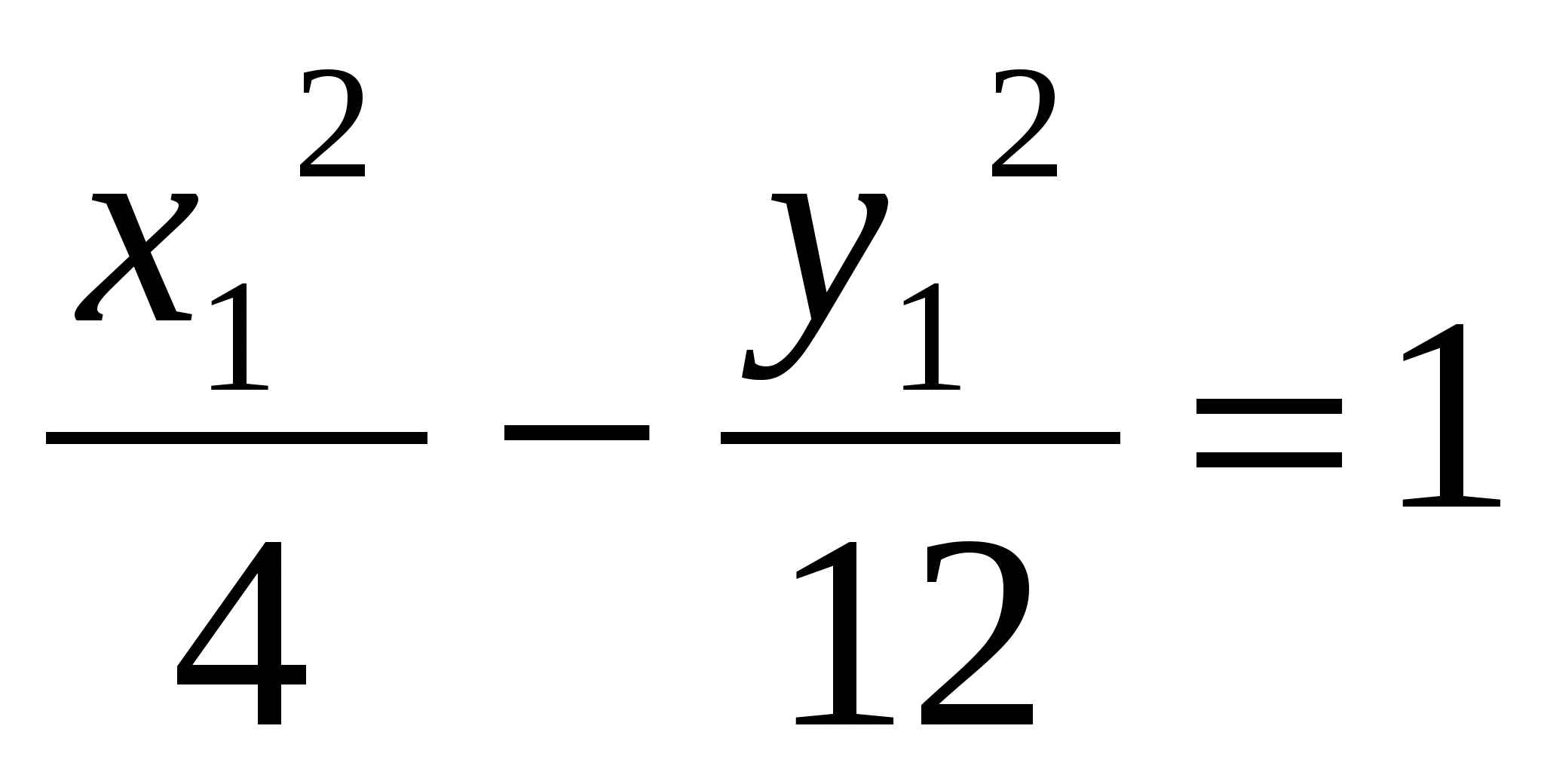 в системе координат в системе координат 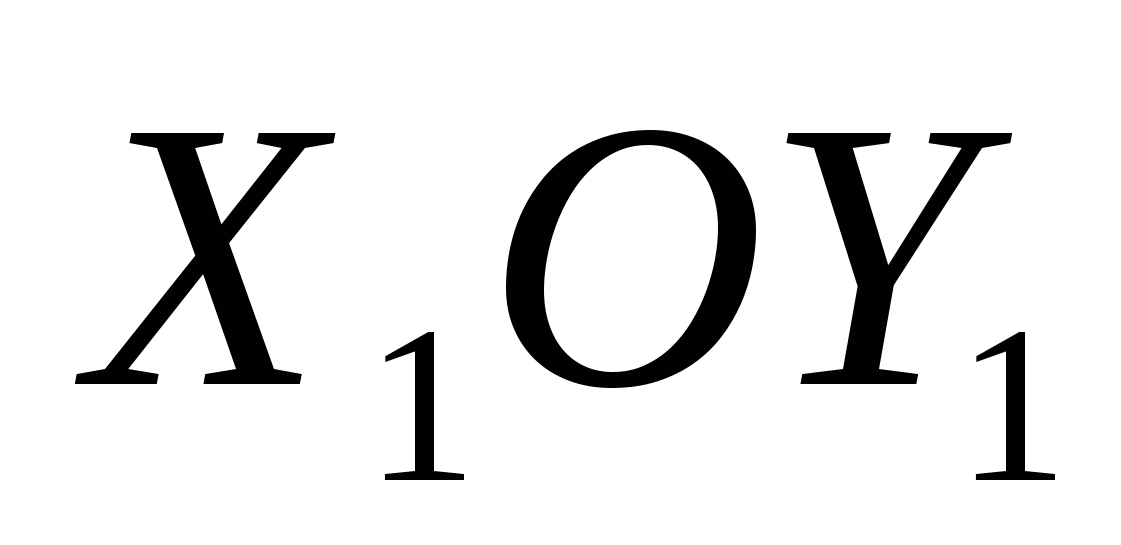 , где , где 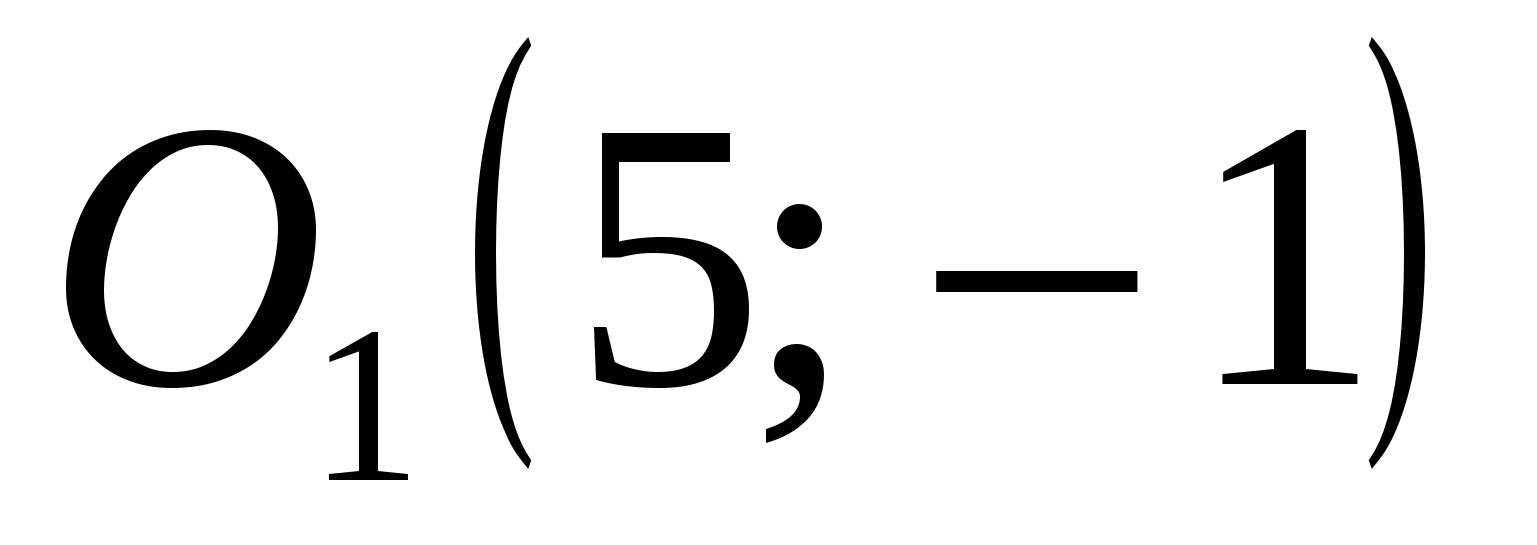 в системе в системе 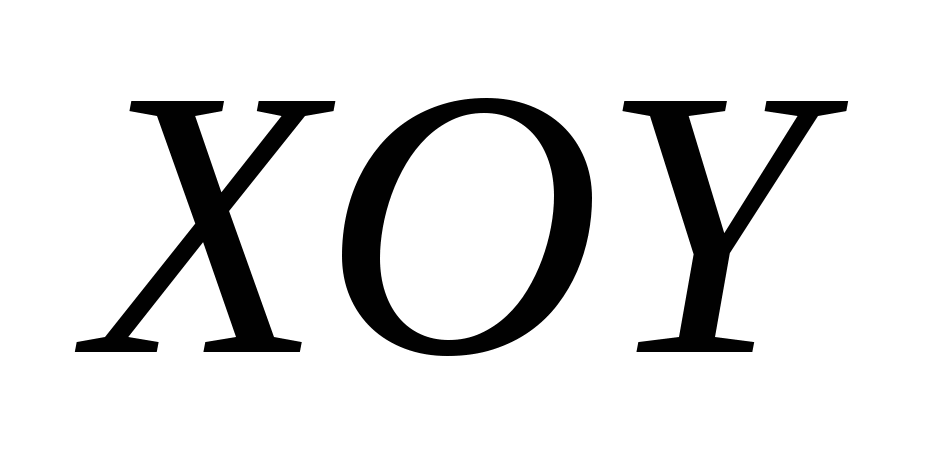 . .
Найдем характерные элементы гиперболы: 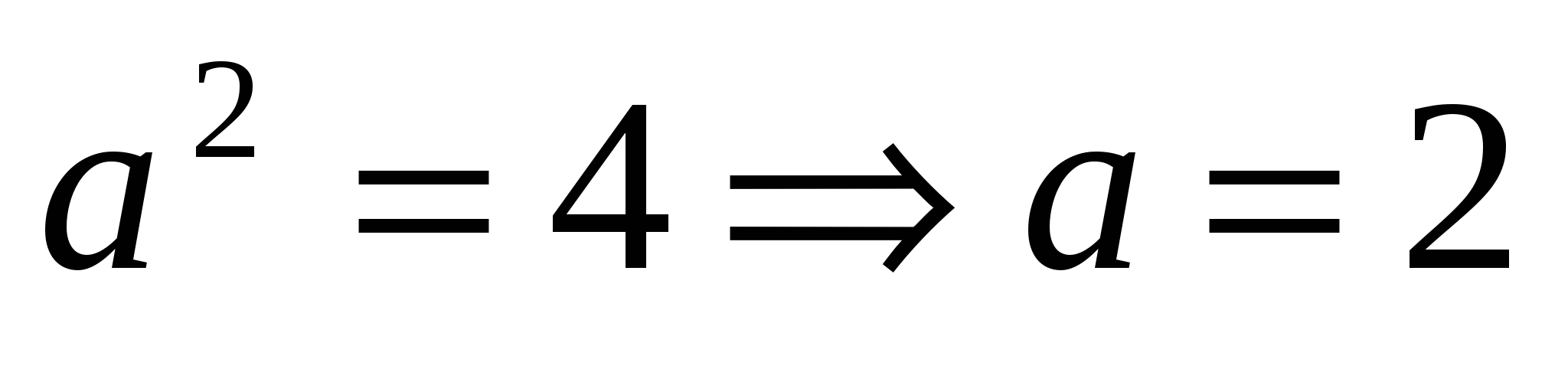 ; ; 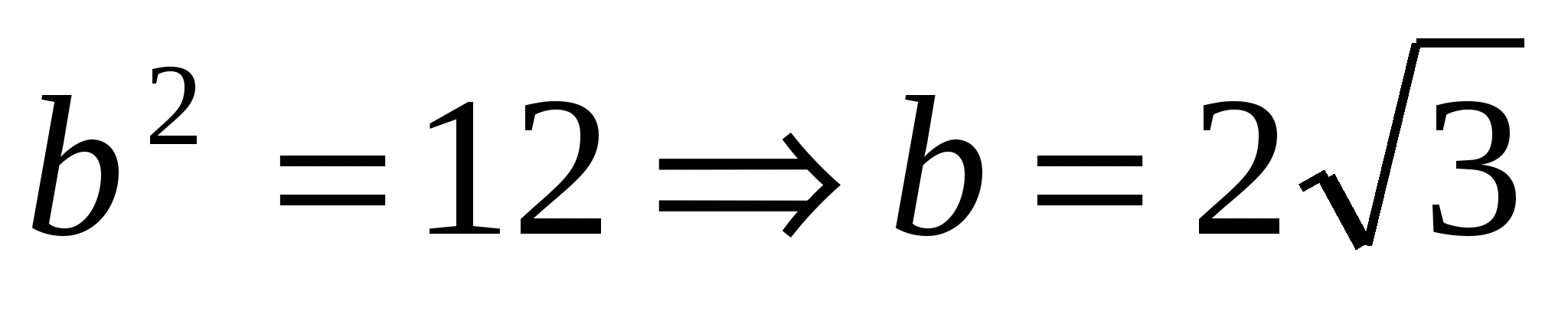 ; ; 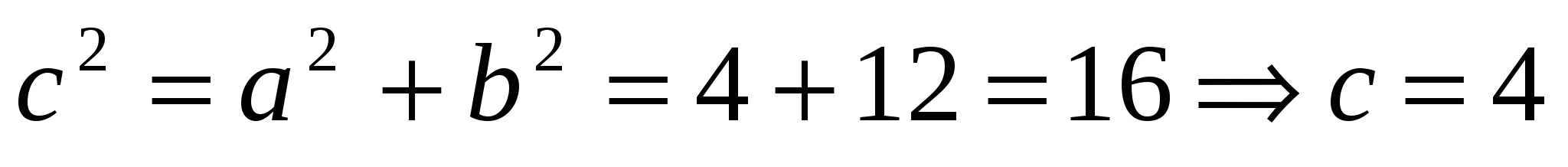 . .
Отсюда получаем: 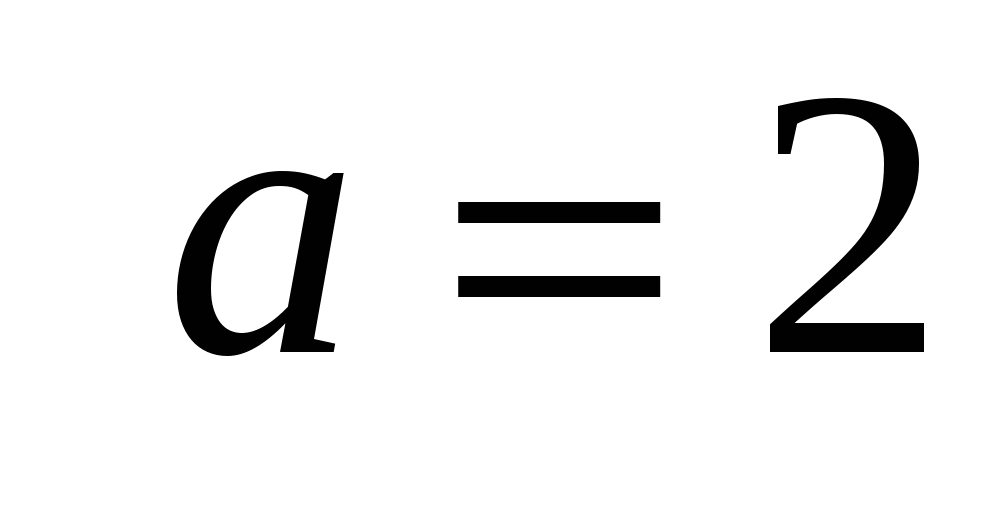 - вещественная полуось гиперболы; - вещественная полуось гиперболы; 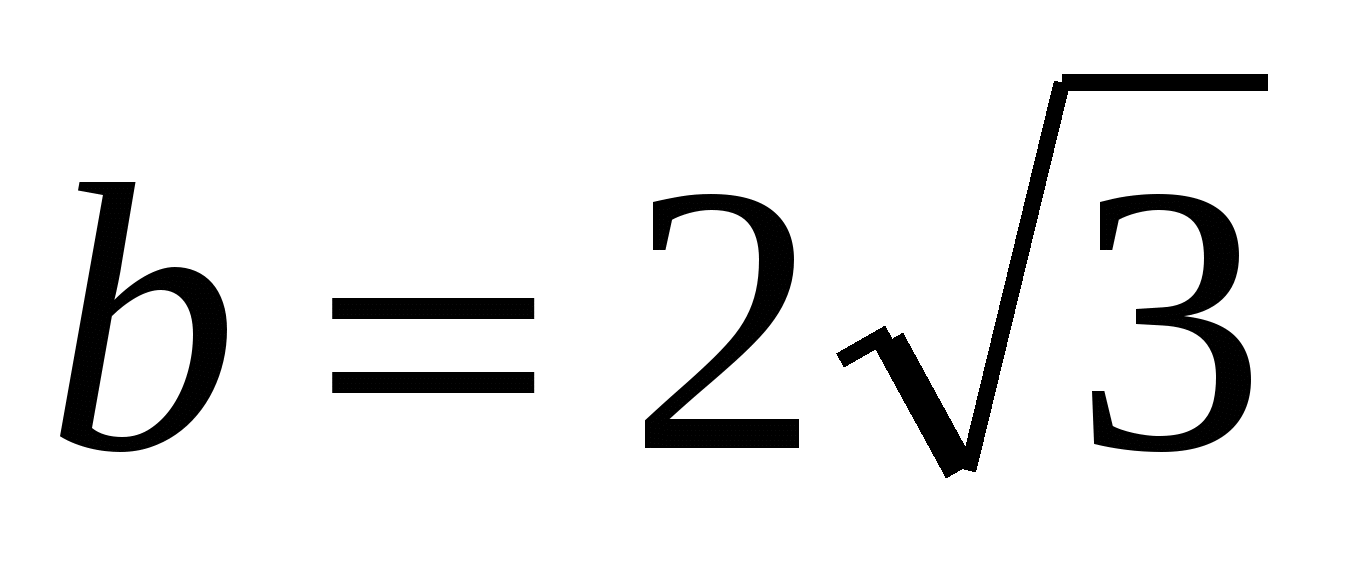 - мнимая полуось гиперболы; - мнимая полуось гиперболы; 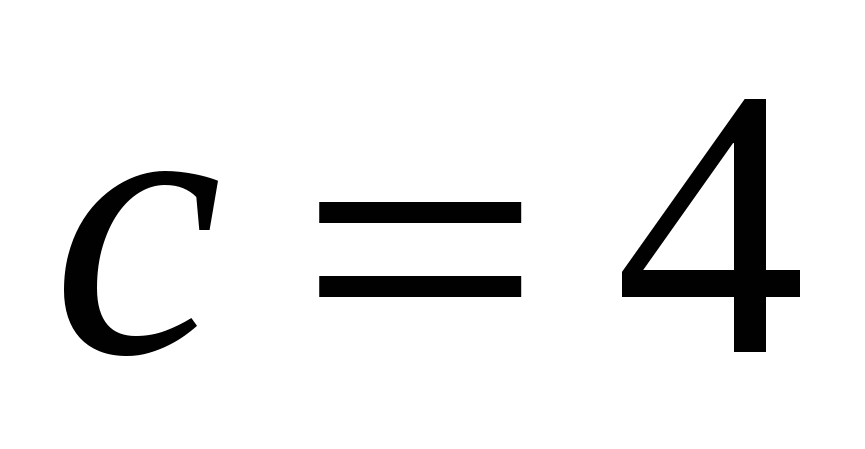 - фокусное расстояние. Координаты фокусов гиперболы в системе координат - фокусное расстояние. Координаты фокусов гиперболы в системе координат 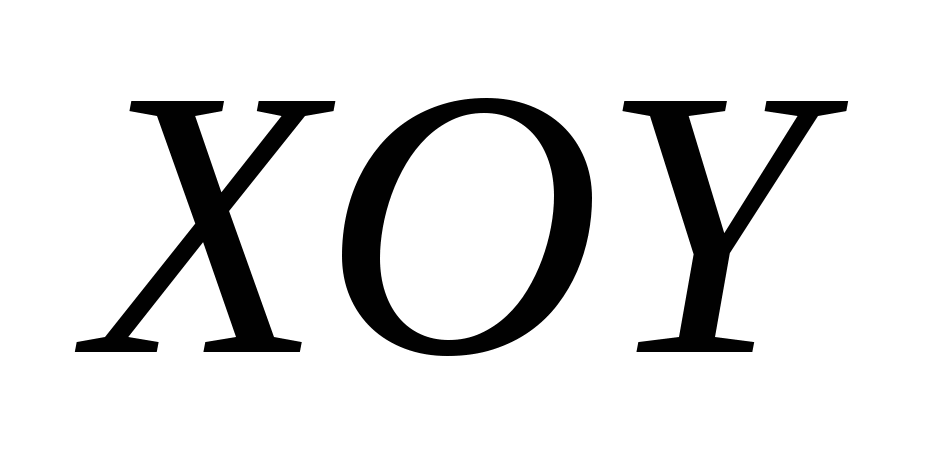 : : 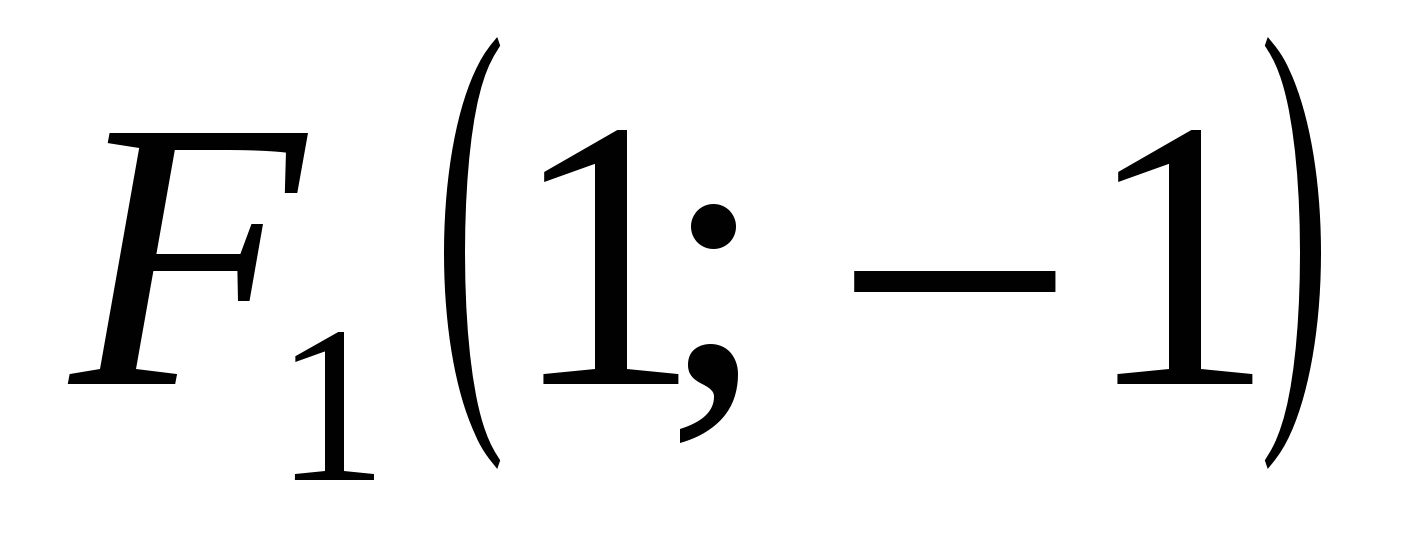 , , 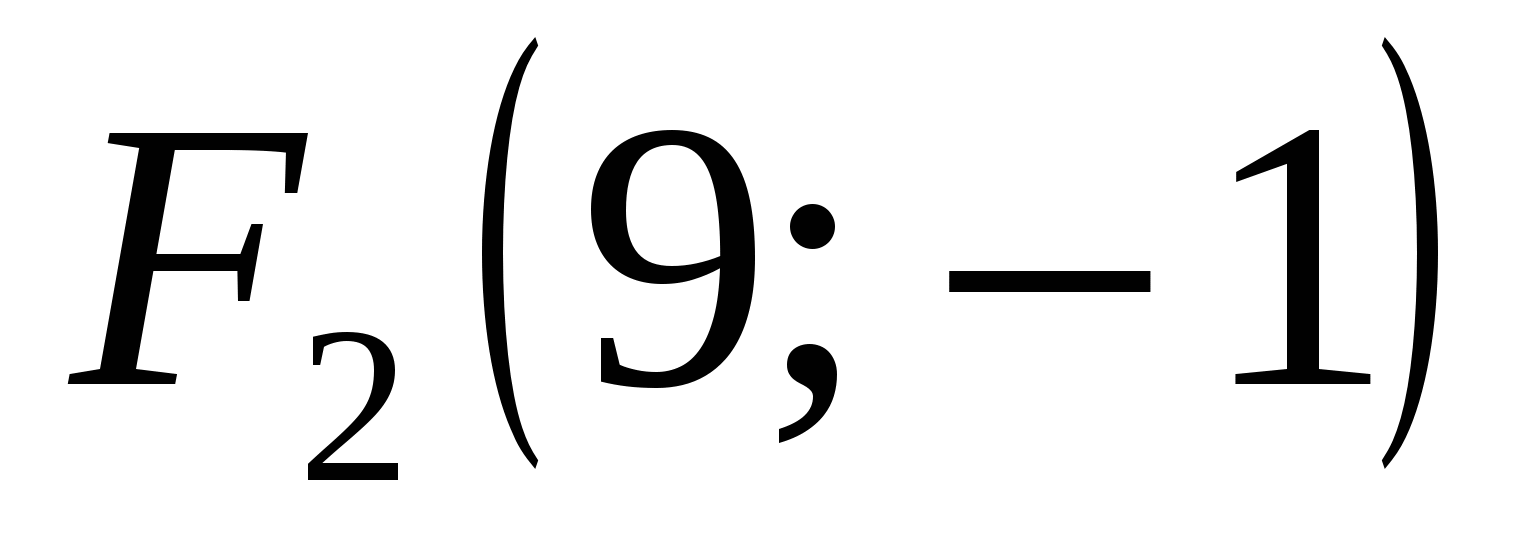 . .
Эксцентриситет гиперболы - 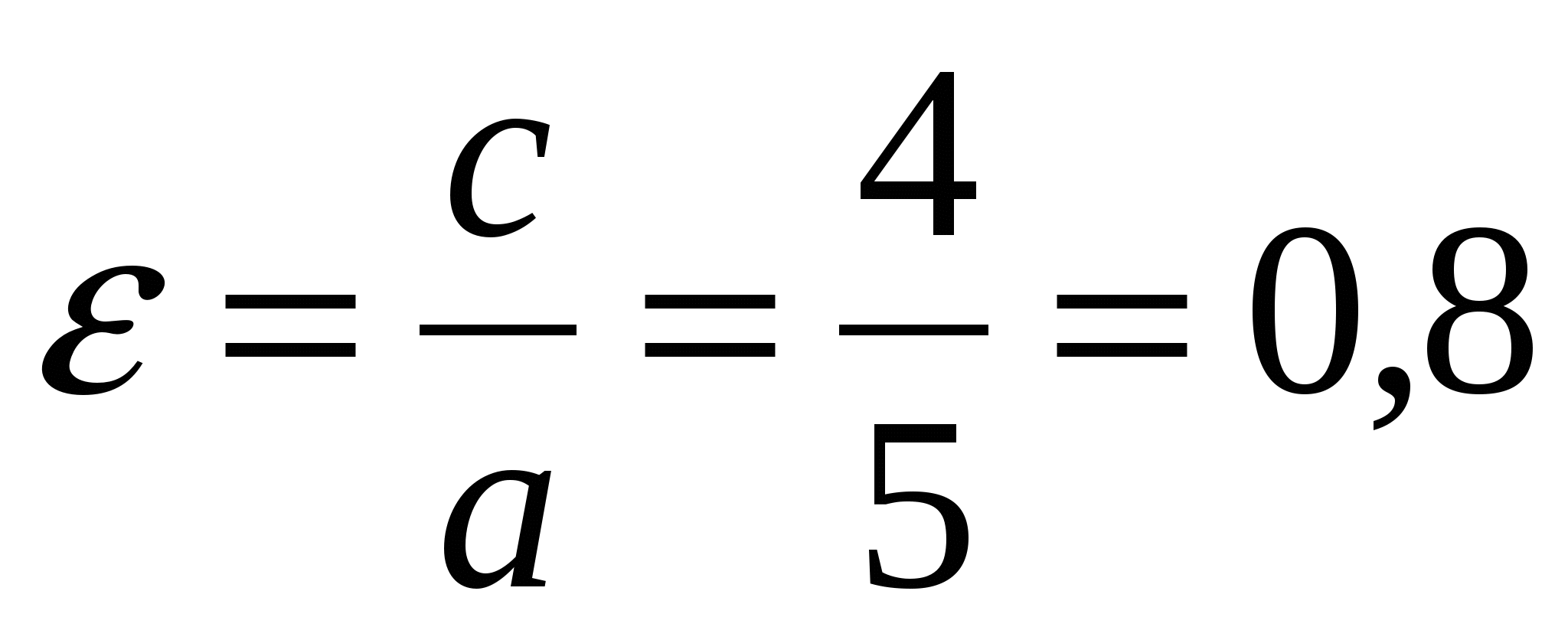
Ответ: 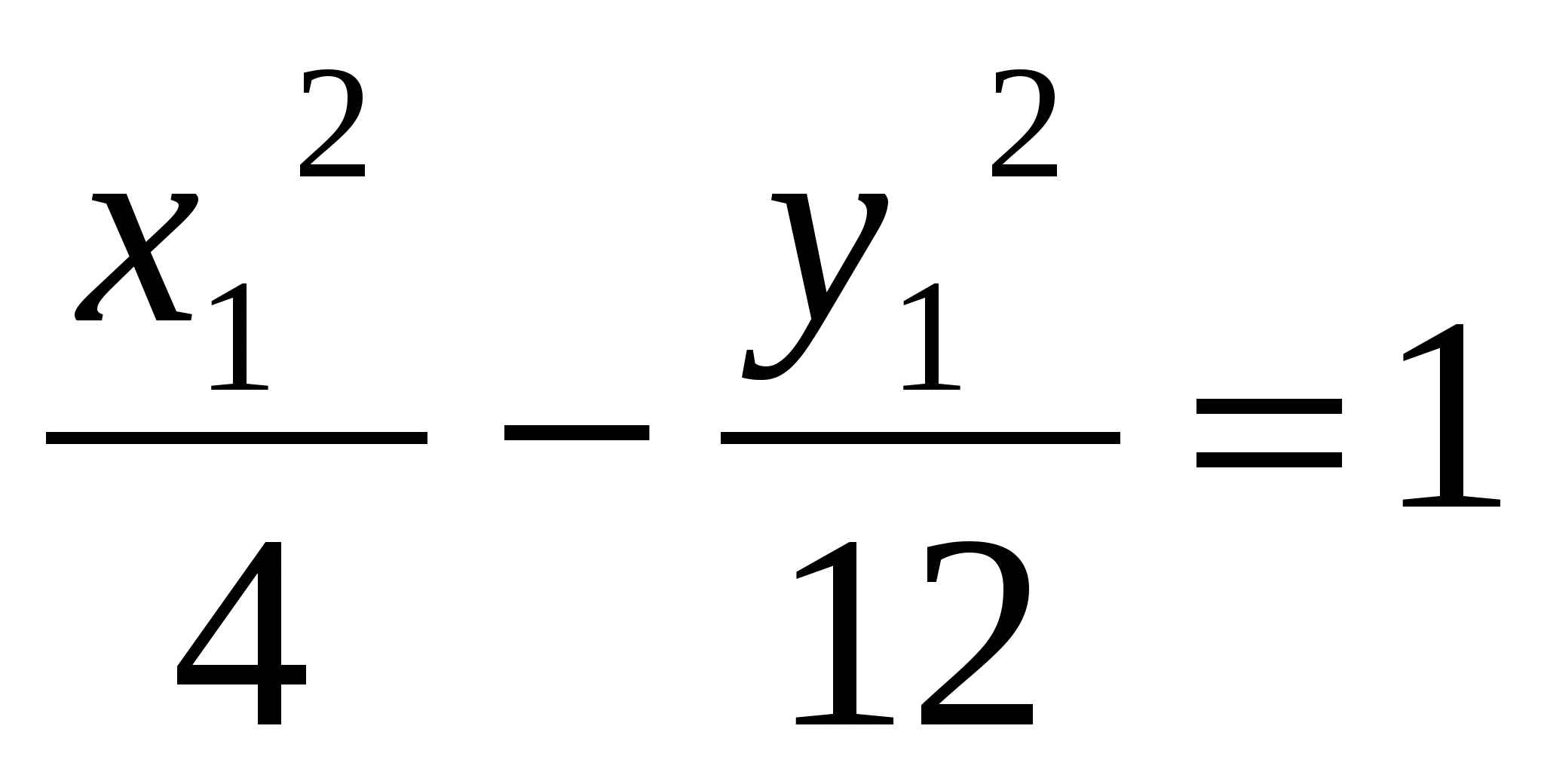 - каноническое уравнение гиперболы, где - каноническое уравнение гиперболы, где 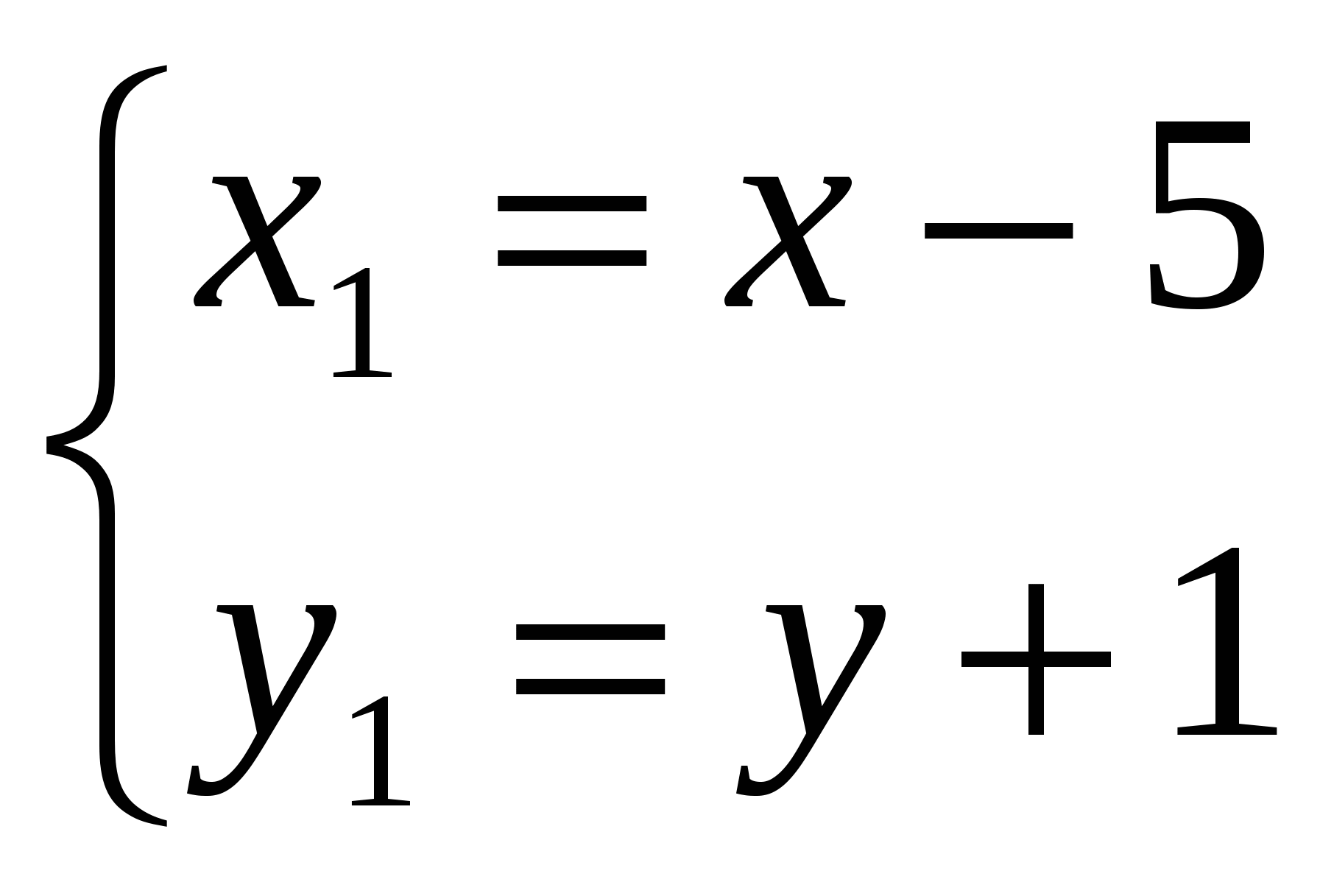 . Характерные элементы: . Характерные элементы:
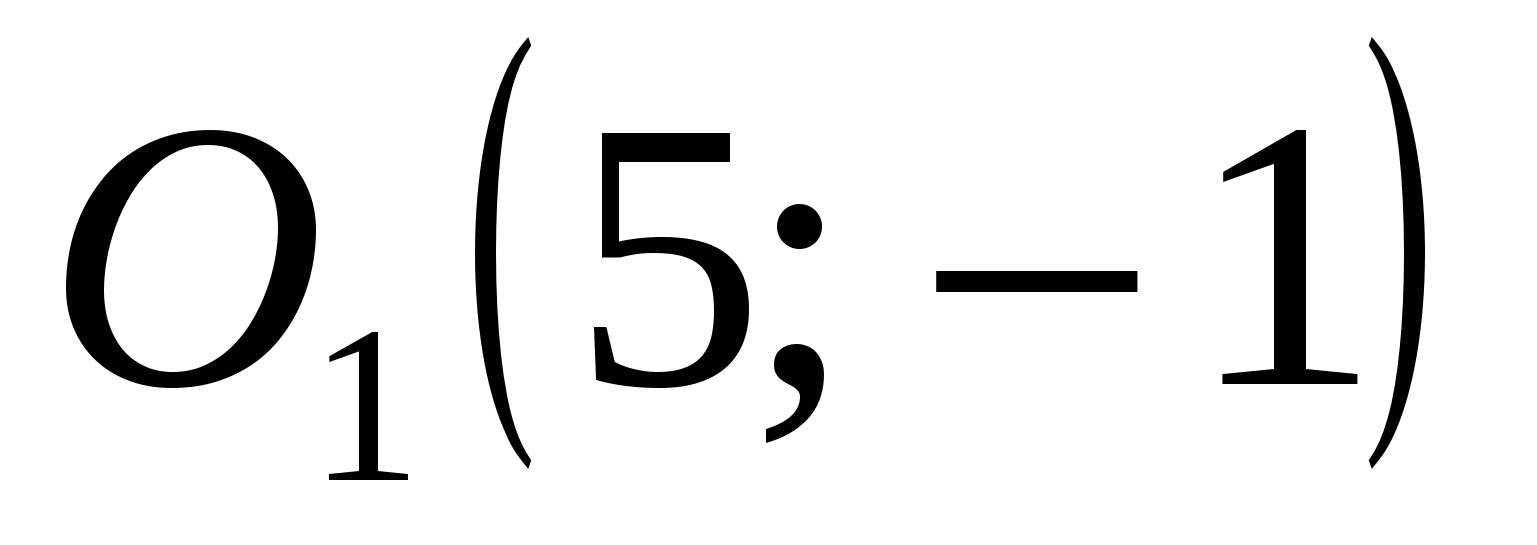 - центр гиперболы; - центр гиперболы;
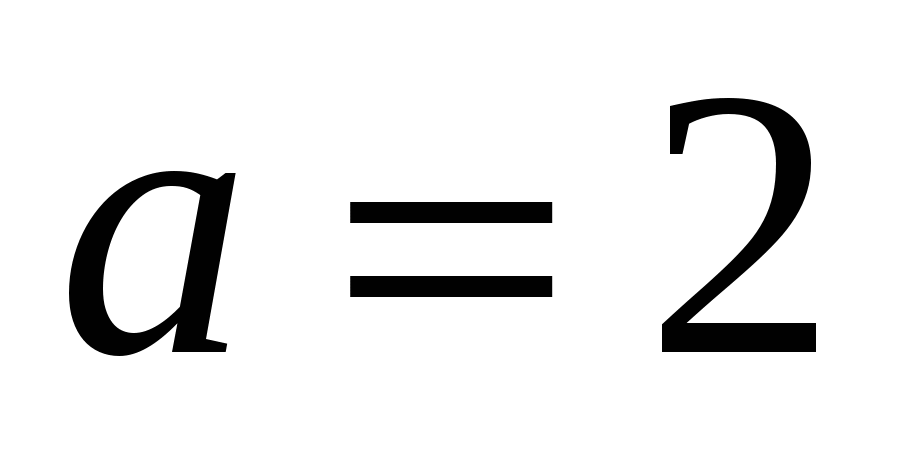 - вещественная полуось гиперболы; - вещественная полуось гиперболы;
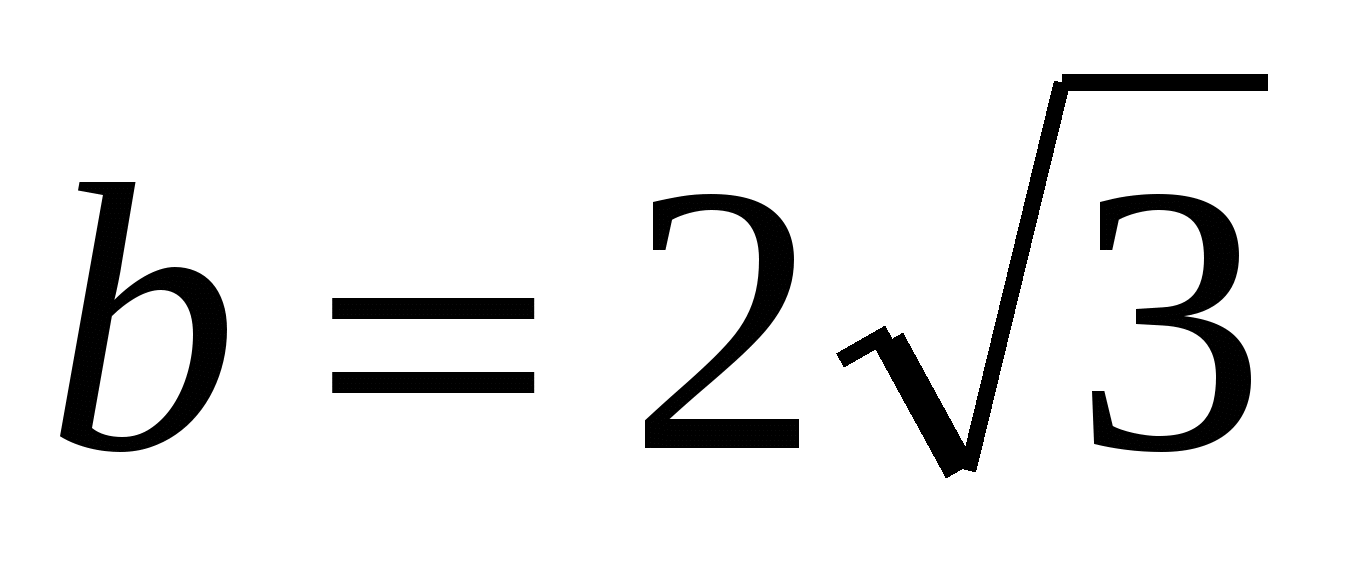 - мнимая полуось гиперболы; - мнимая полуось гиперболы;
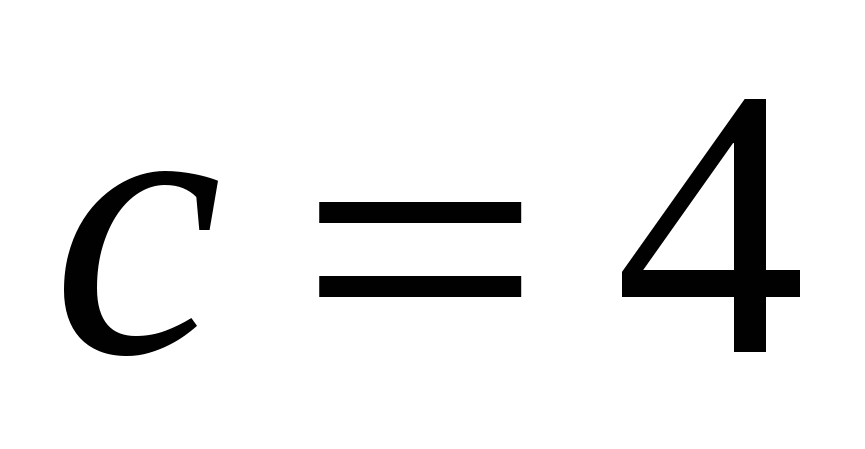 - фокусное расстояние; - фокусное расстояние;
координаты фокусов гиперболы в системе координат 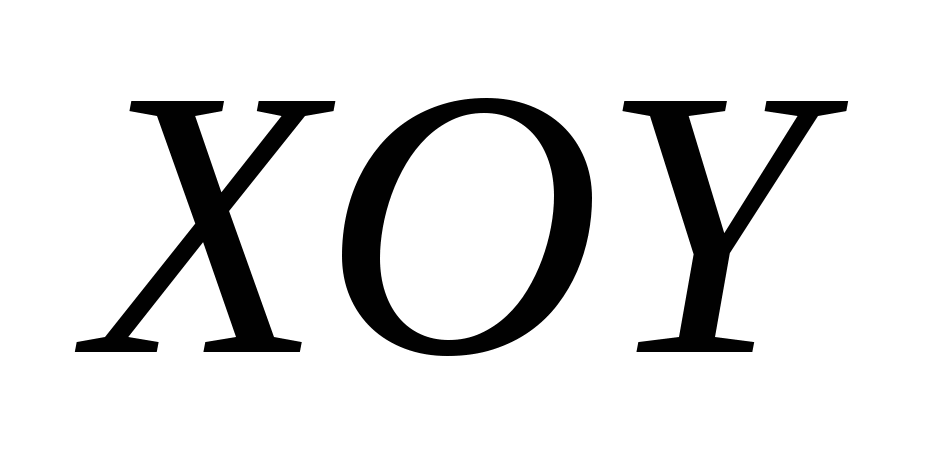 : : 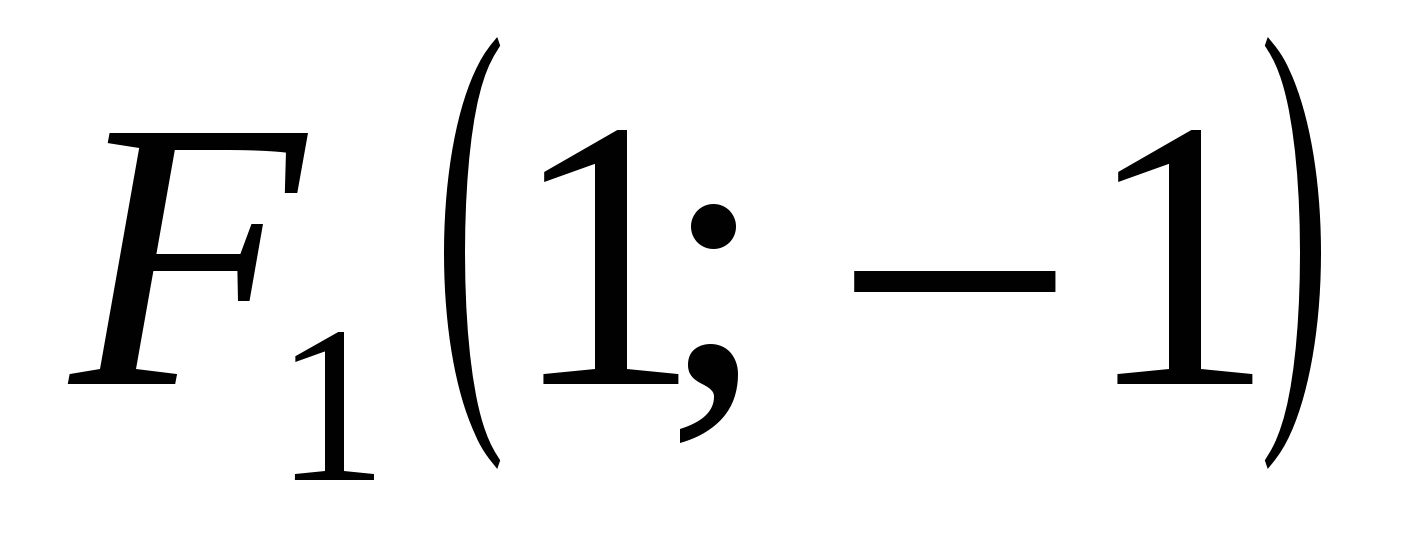 , , 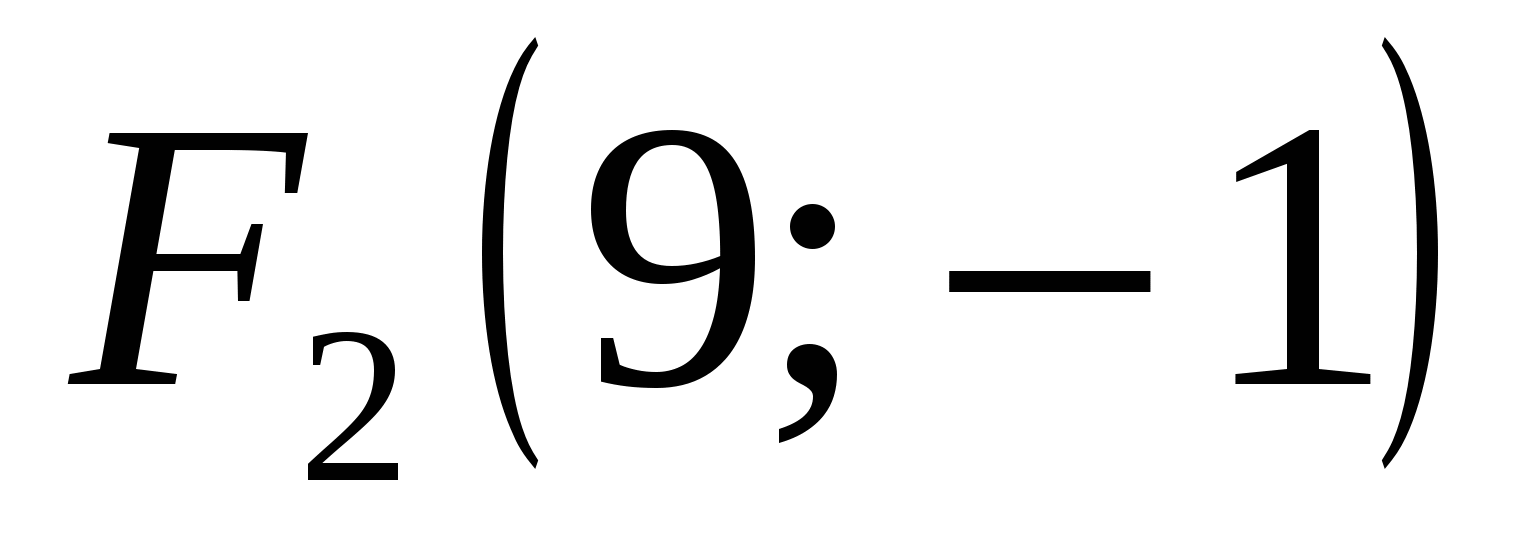 . .

Задача 4. Даны уравнение кривой второго порядка 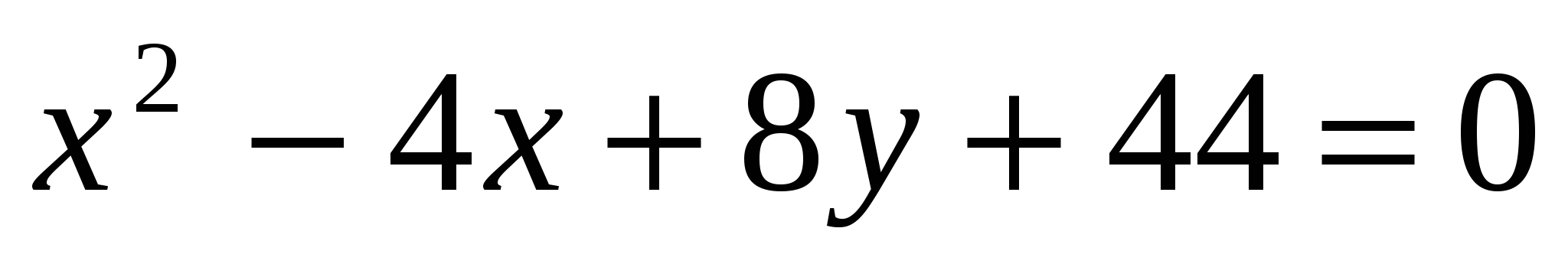 и уравнение прямой и уравнение прямой 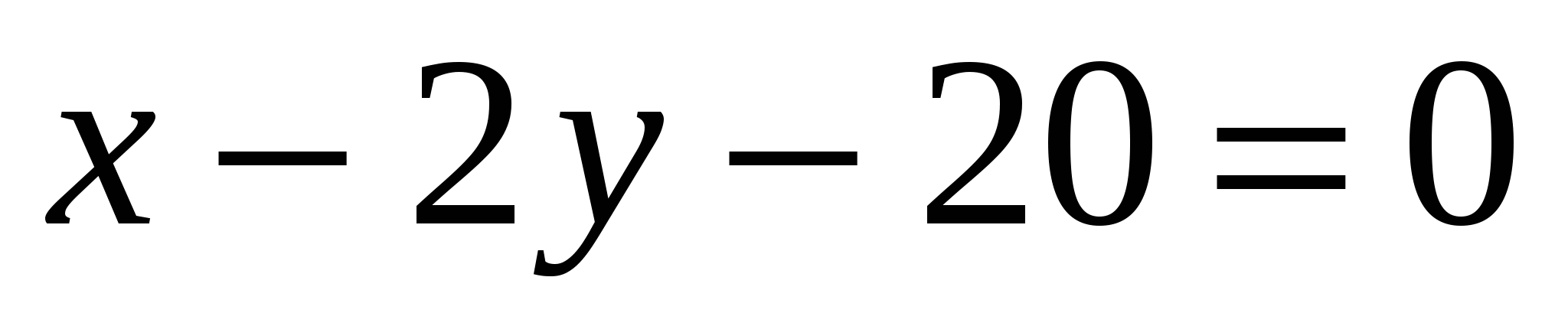 . Требуется: . Требуется:
привести заданное уравнение кривой второго порядка к каноническому виду;
найти точки пересечения кривой и заданной прямой;
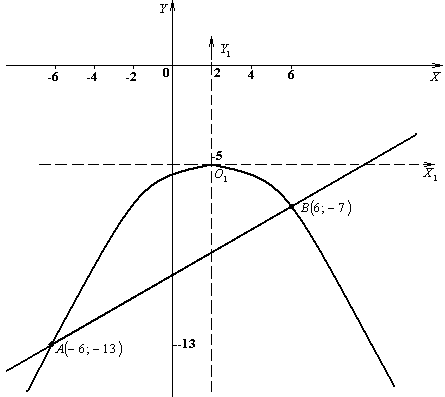
построить обе линии в исходной системе координат
Решение
1) Выделим в уравнении полный квадрат по переменной 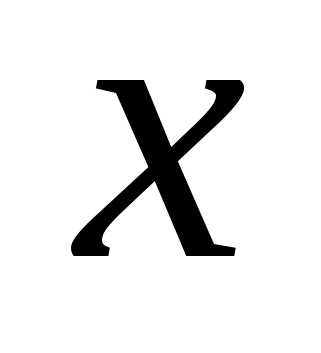 . .
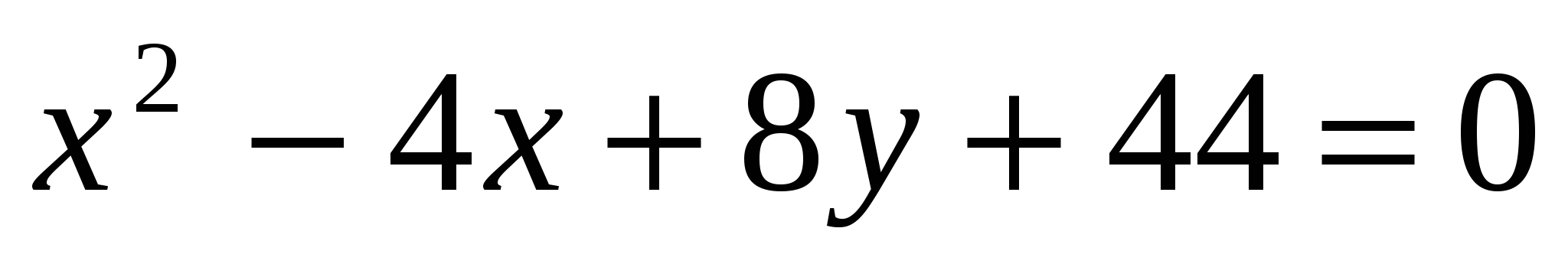
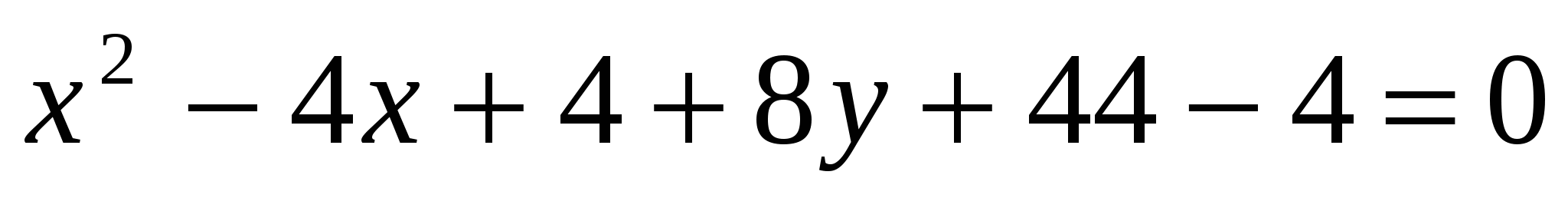
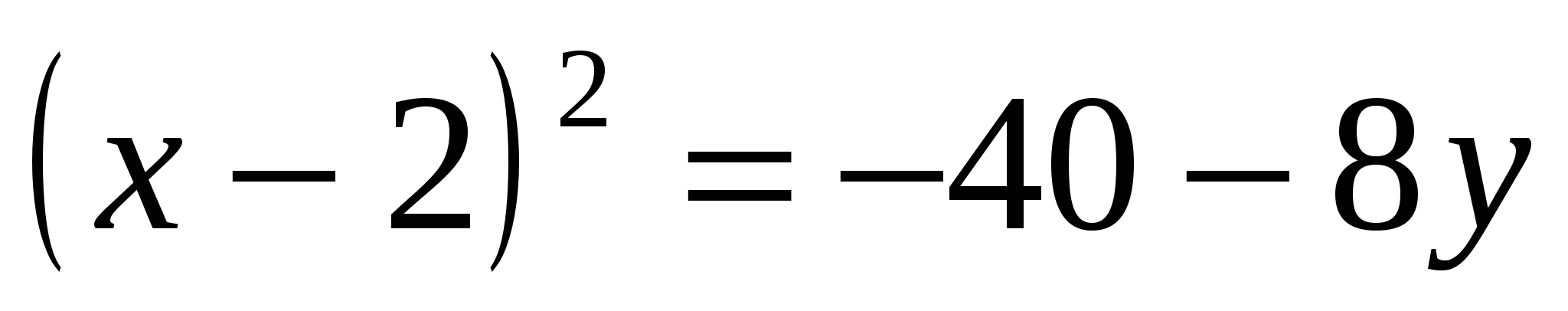
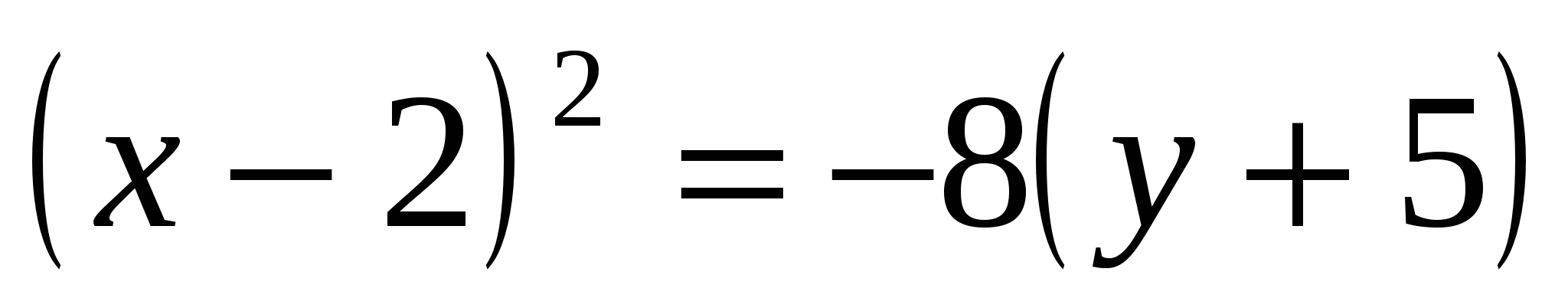
Получили уравнение параболы вида  с вершиной в точке с вершиной в точке 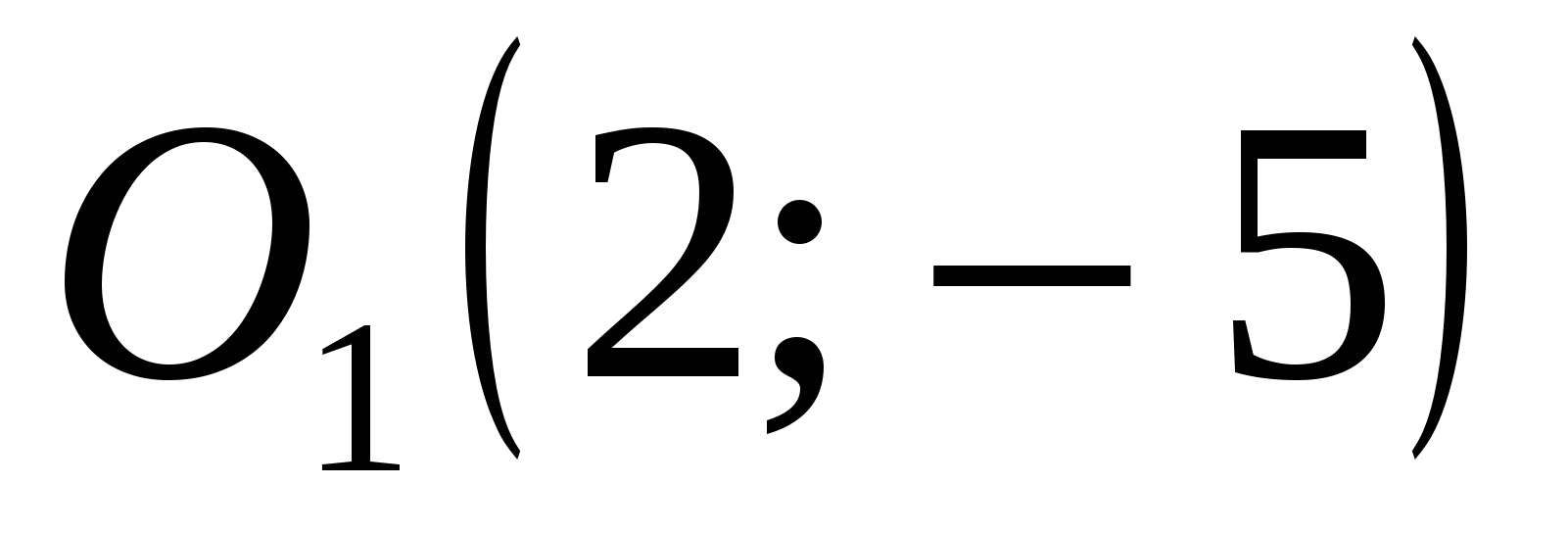 . Осуществив параллельный перенос осей координат в системе . Осуществив параллельный перенос осей координат в системе 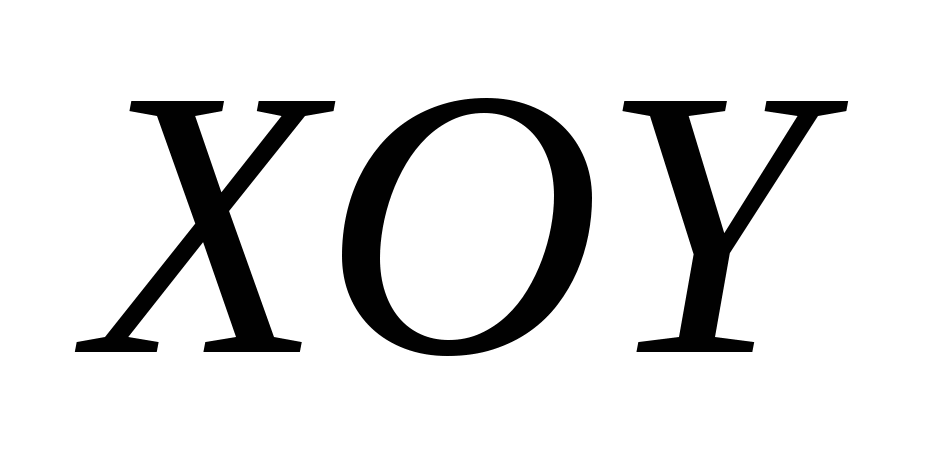 по формулам по формулам 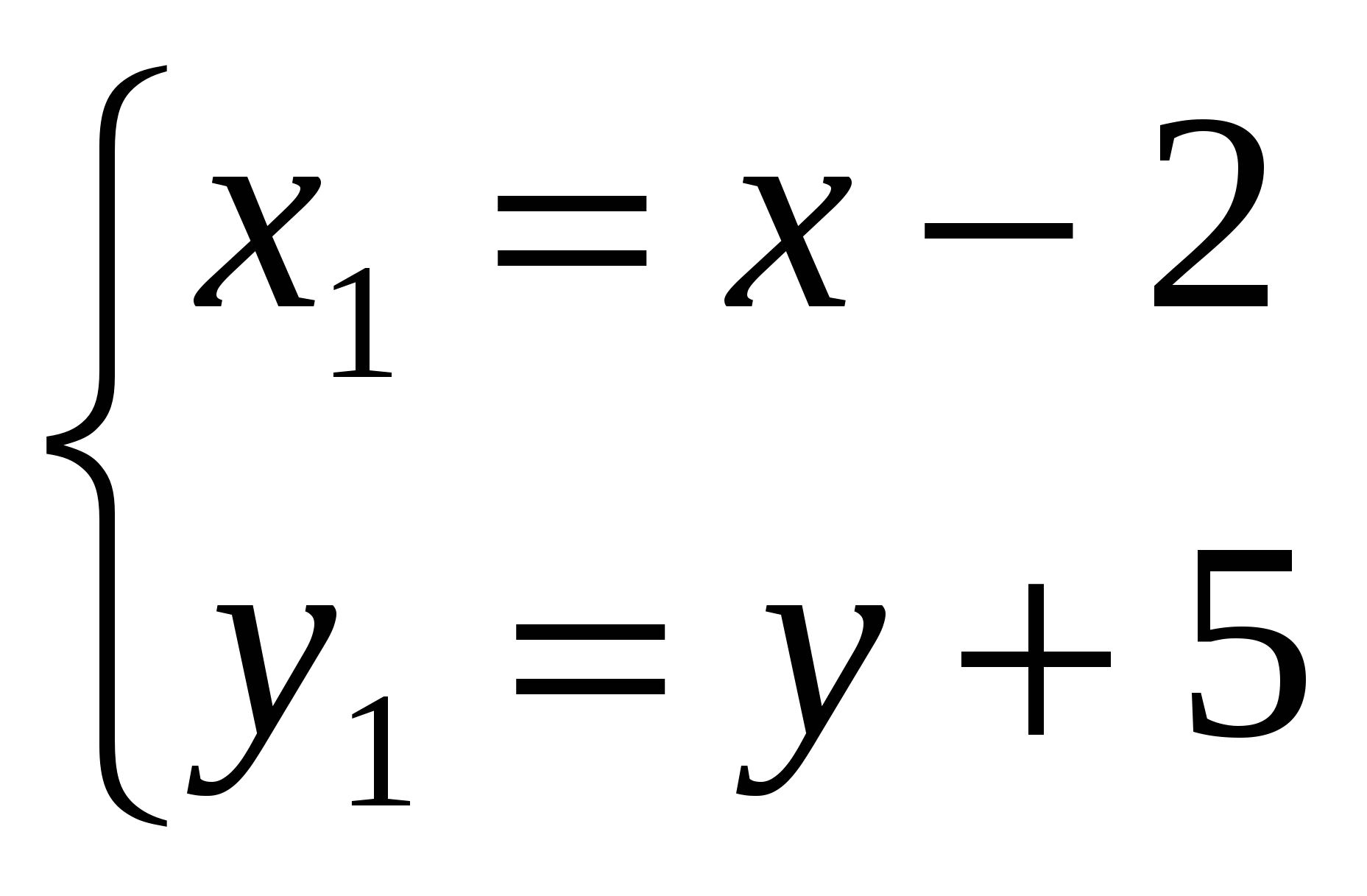 , получим каноническое уравнение гиперболы , получим каноническое уравнение гиперболы 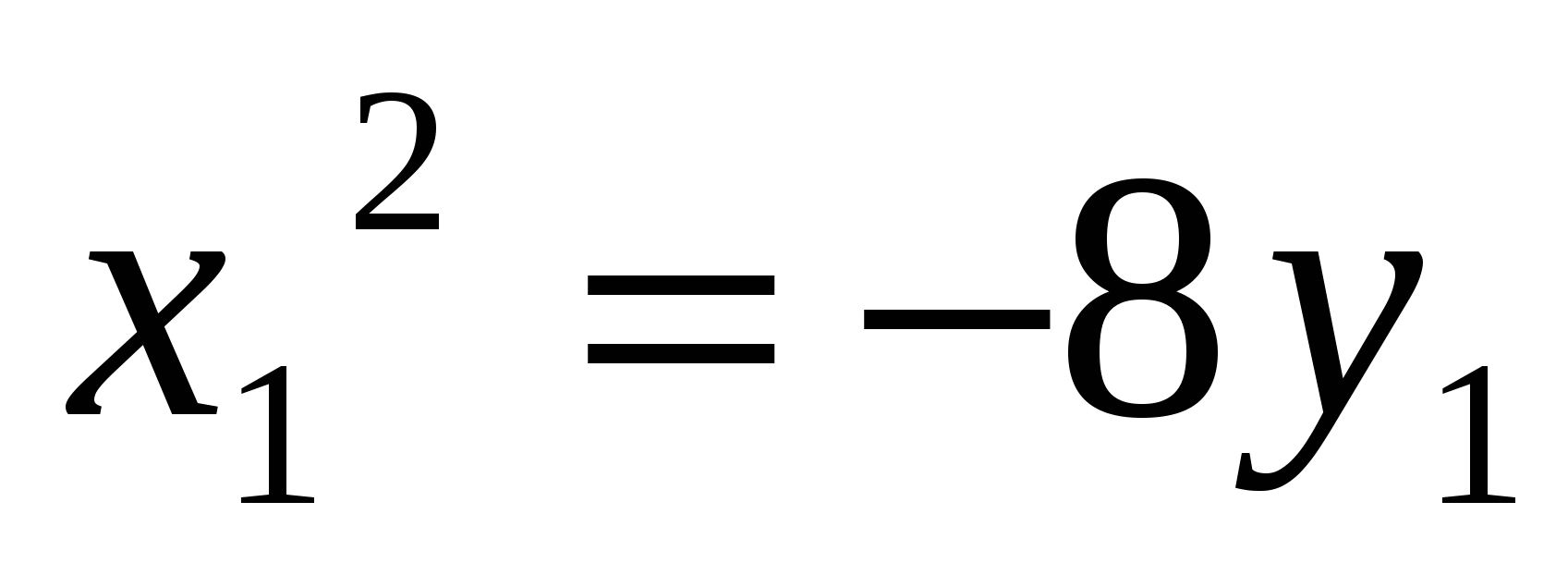 в системе координат в системе координат 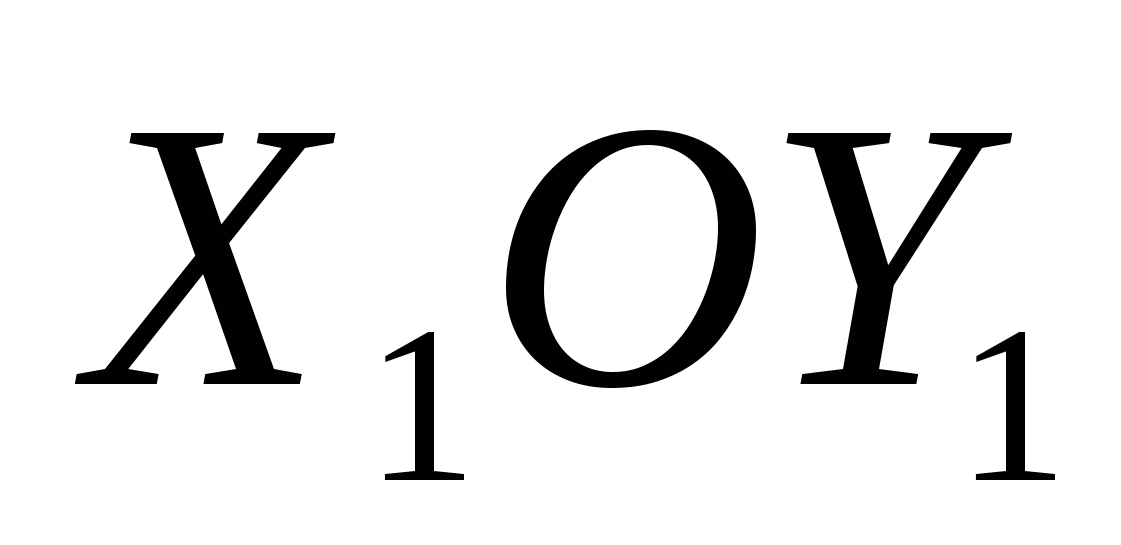 . .
2) Найдем точки пересечения параболы и заданной прямой в системе координат 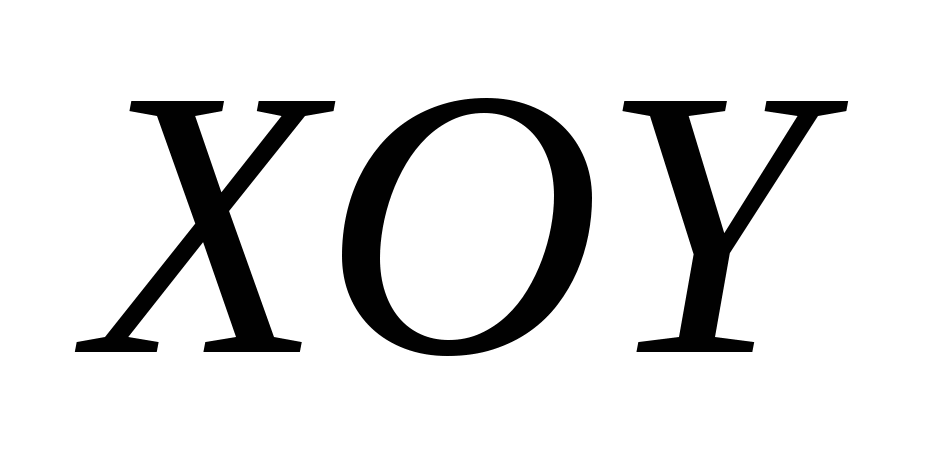 . Для этого решим систему уравнений: . Для этого решим систему уравнений:
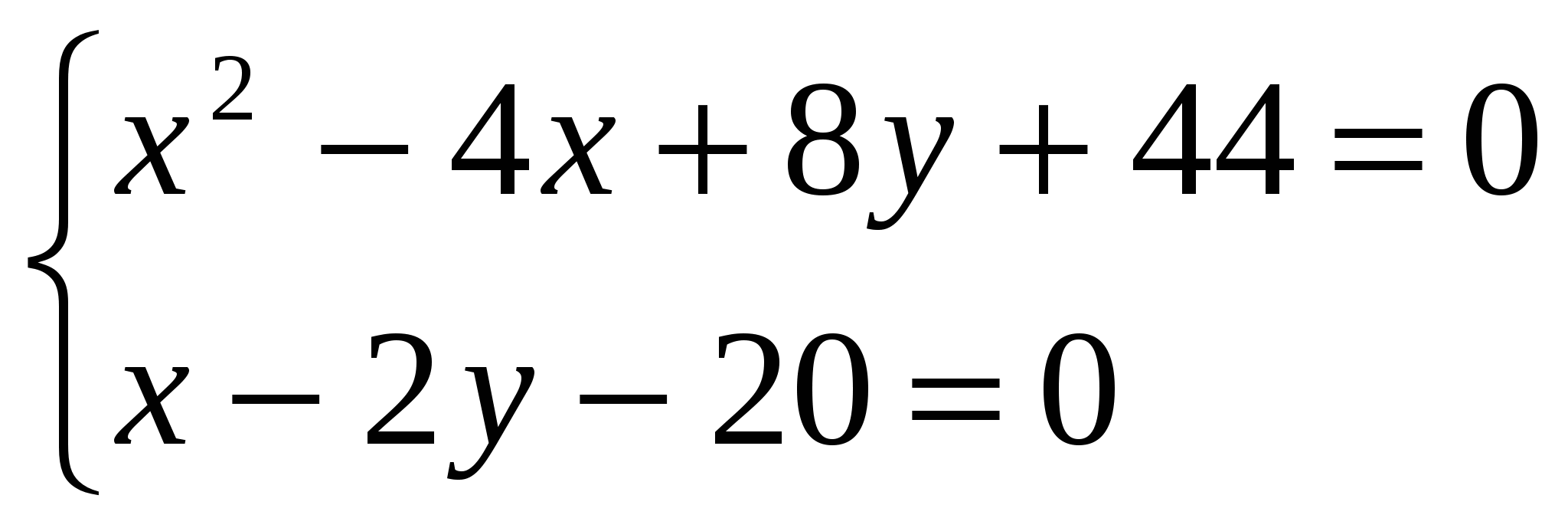 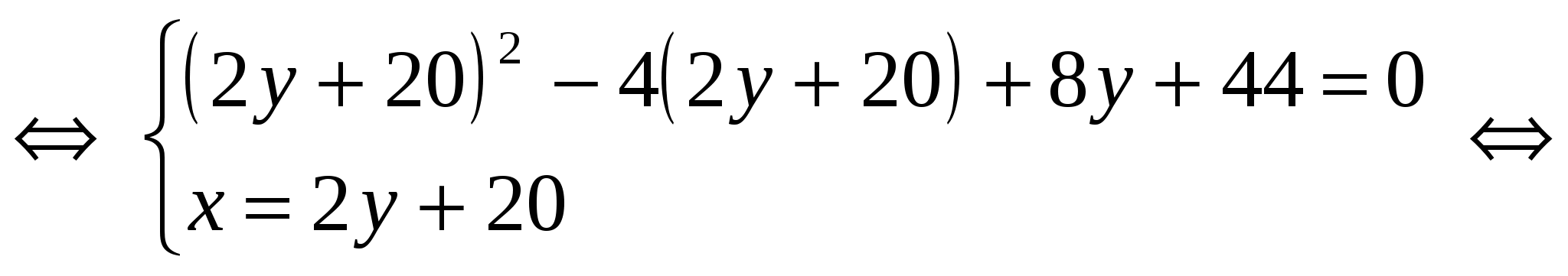
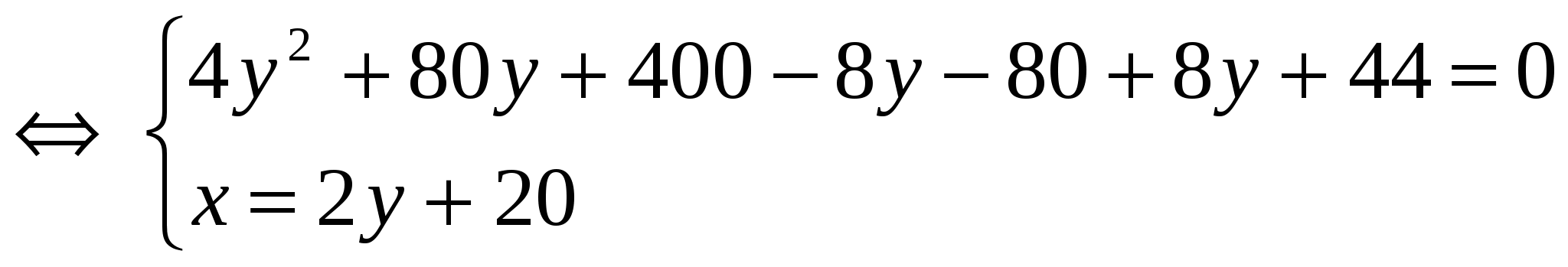 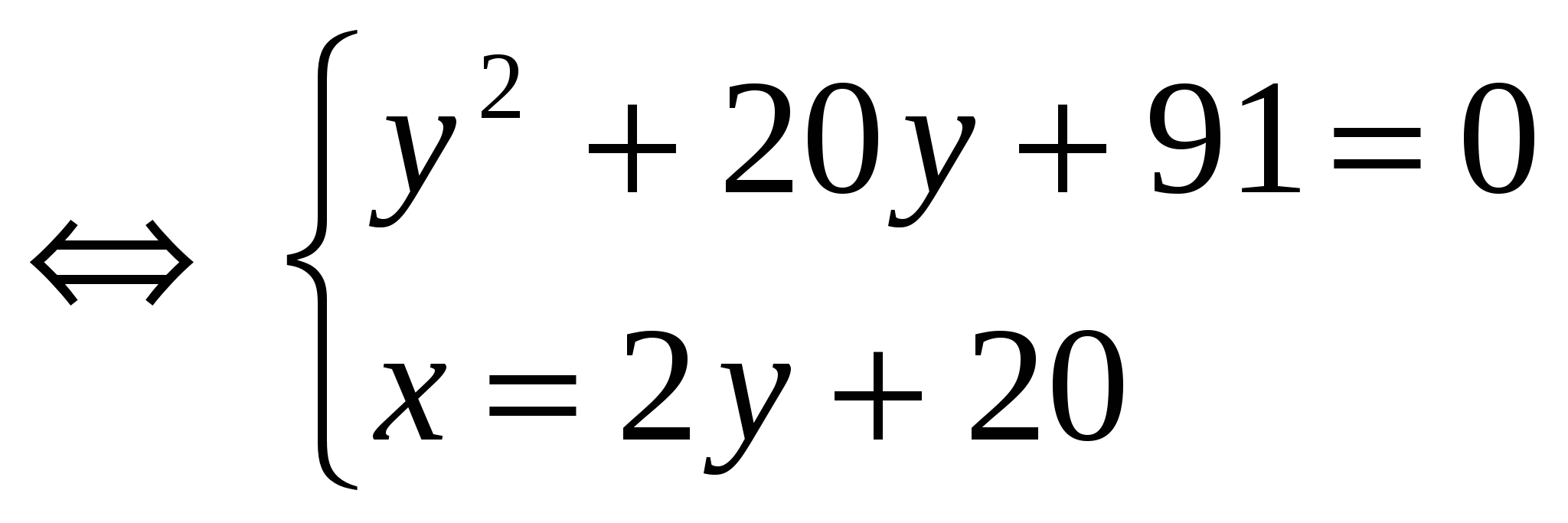
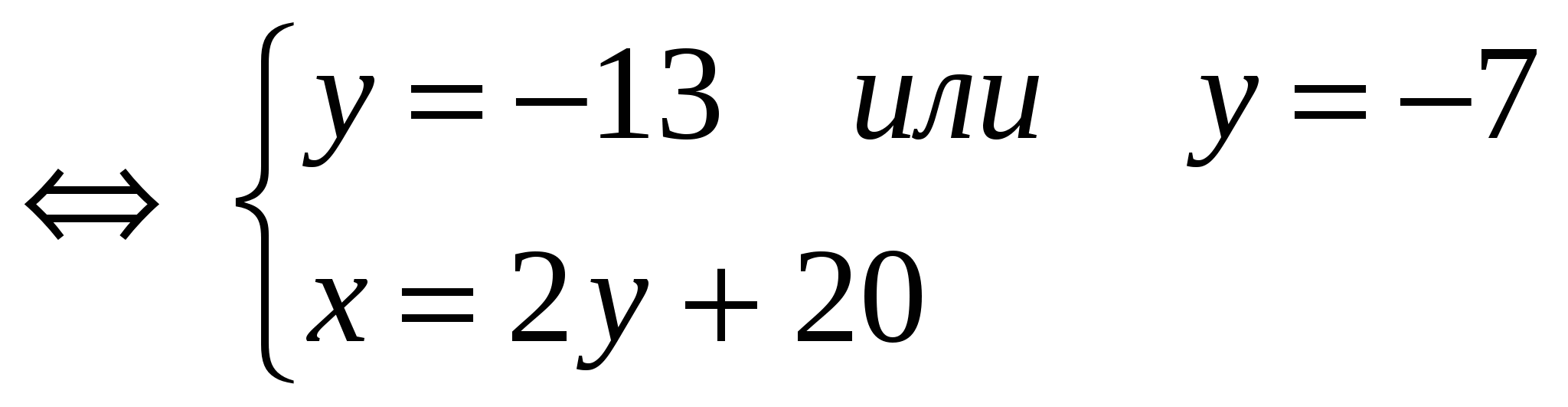 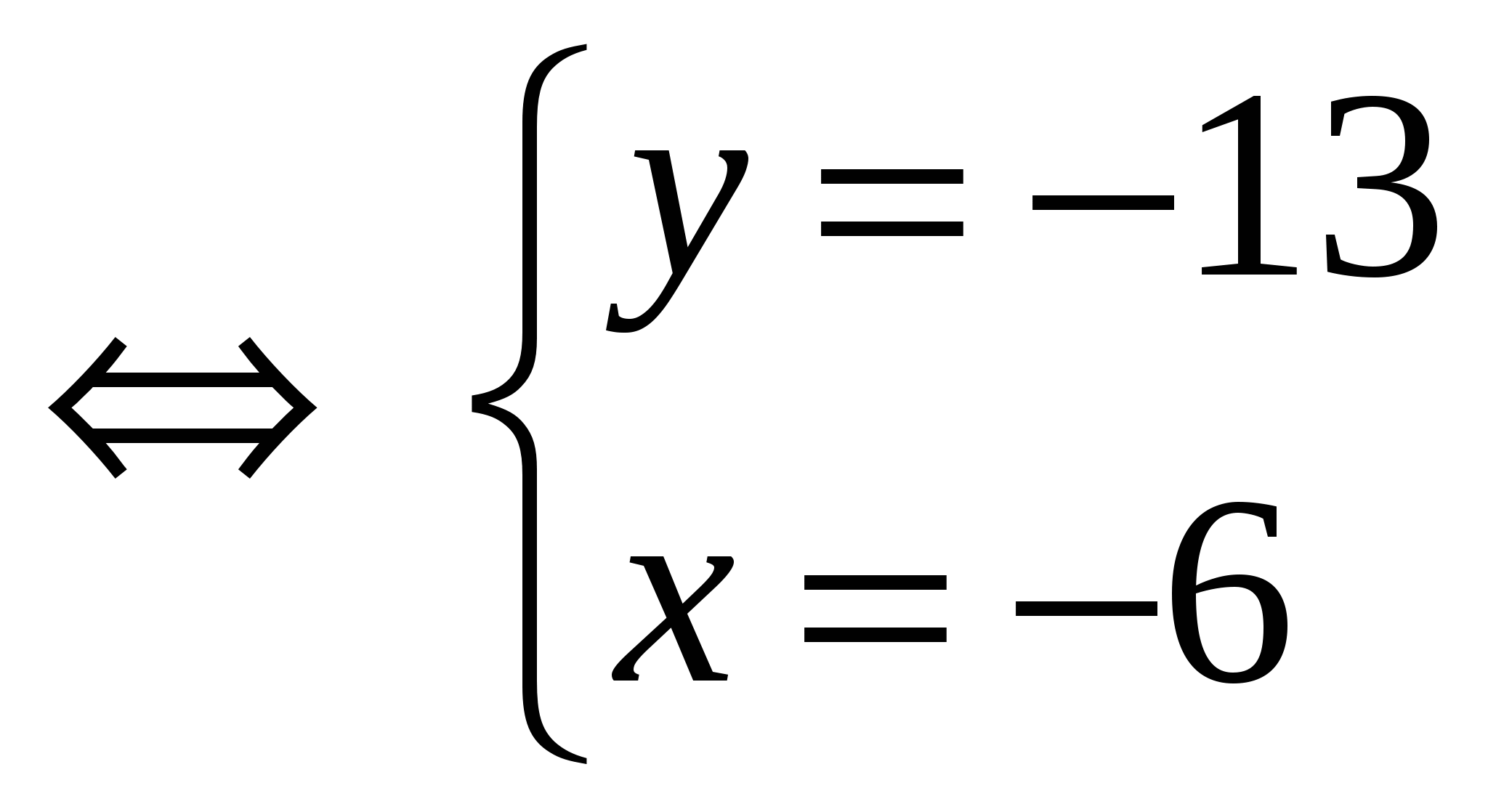 или или 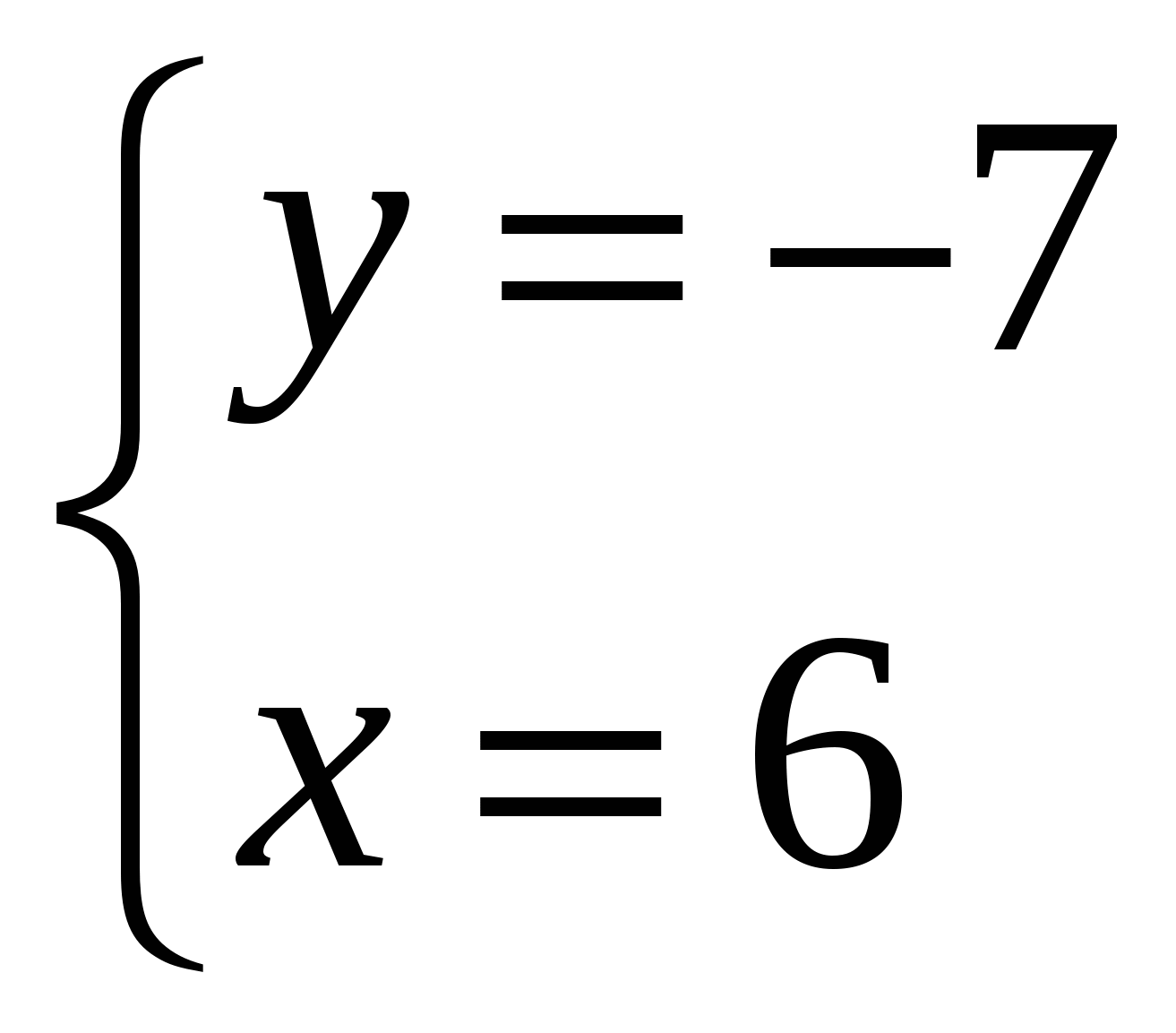
Таким образом, прямая и парабола пересекаются в точках 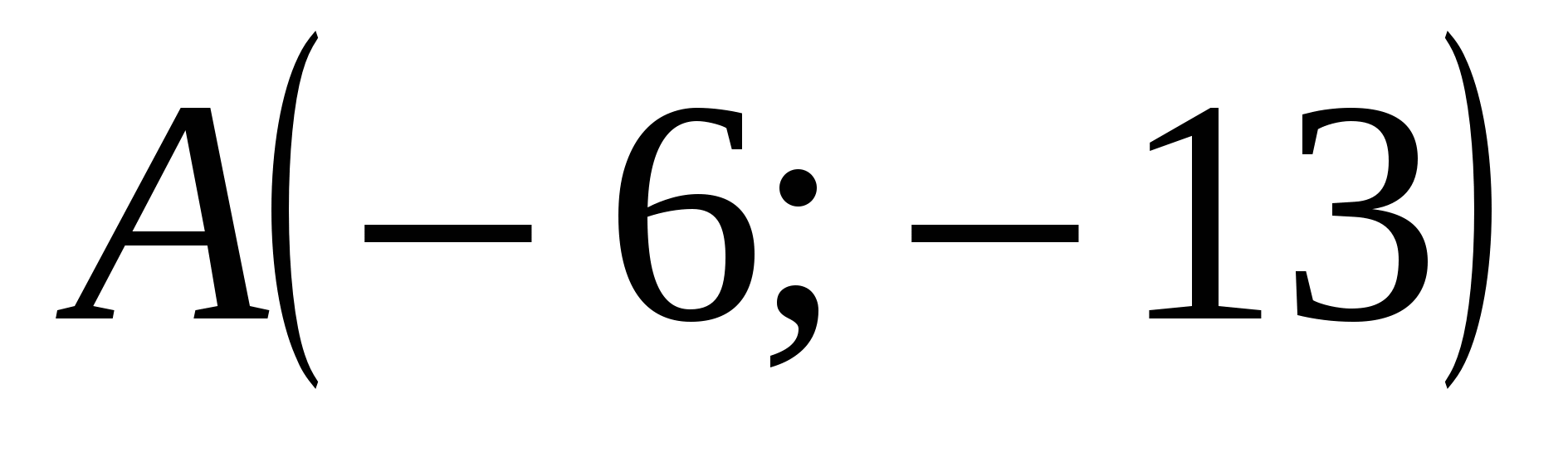 ; ; 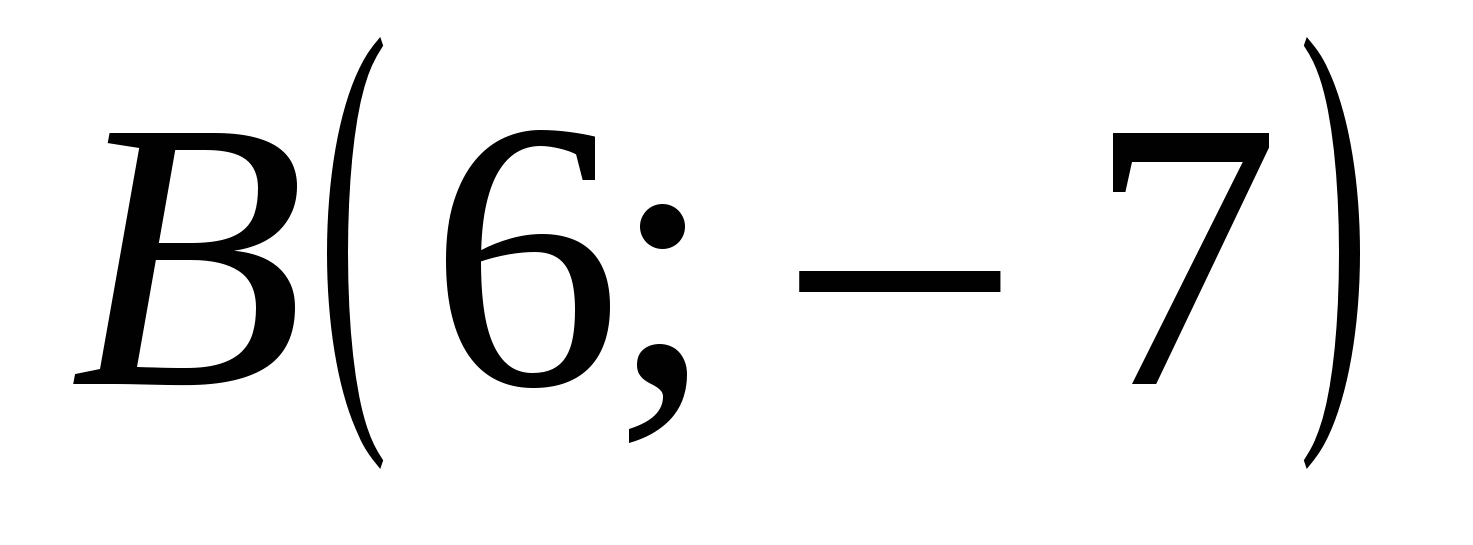 . .
3)
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК) 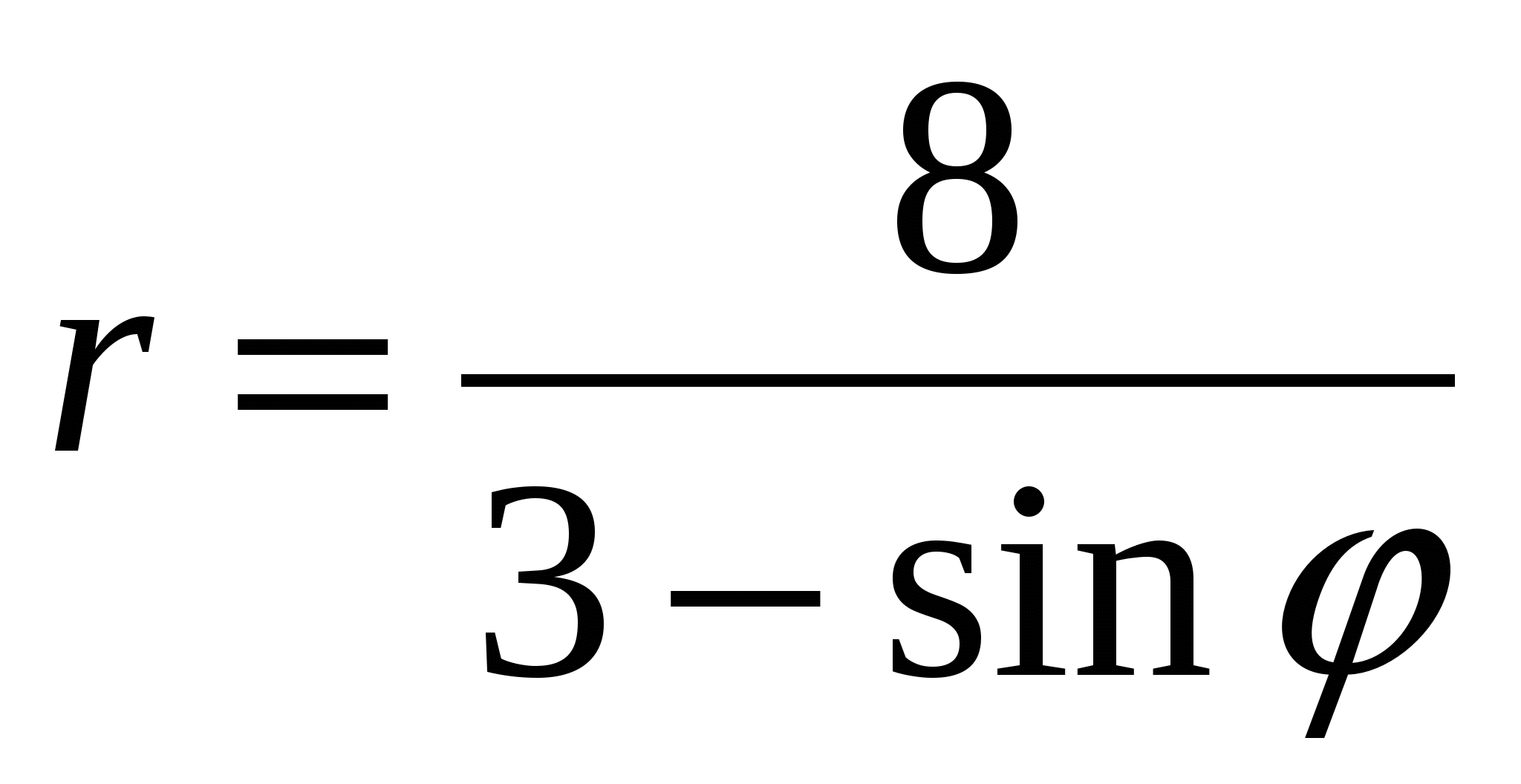 . .
Требуется:
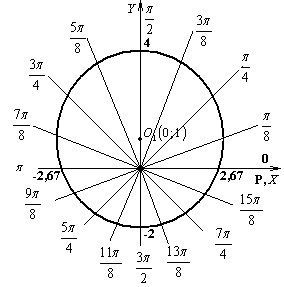
построить область определения функции 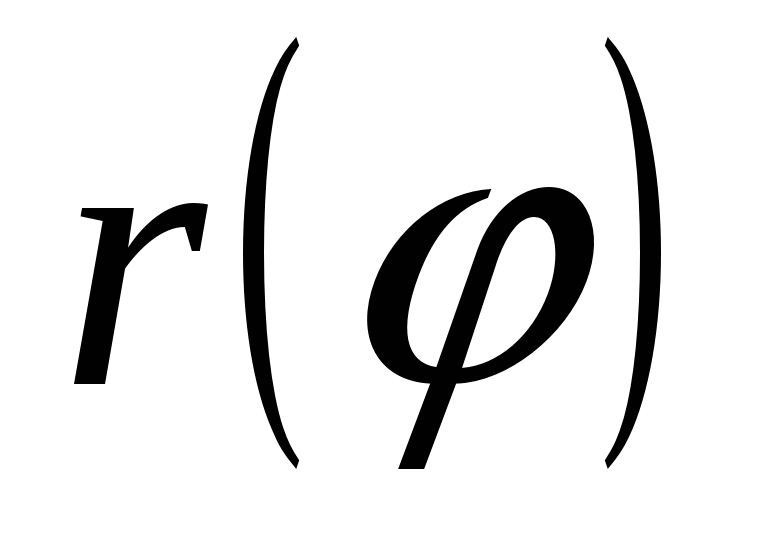 ; ;
построить кривую в ПСК, вычислив значения функции в точках 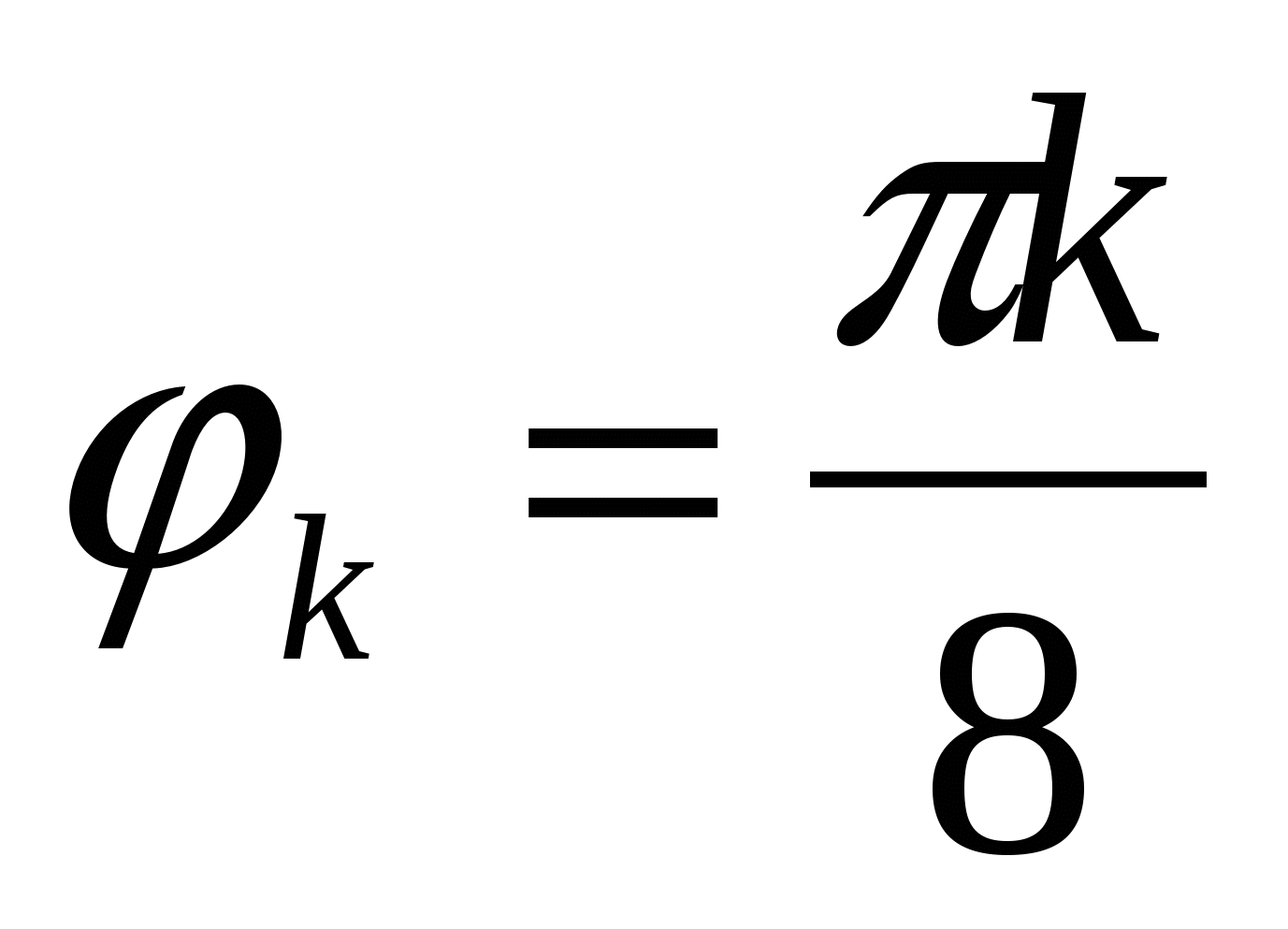 , , 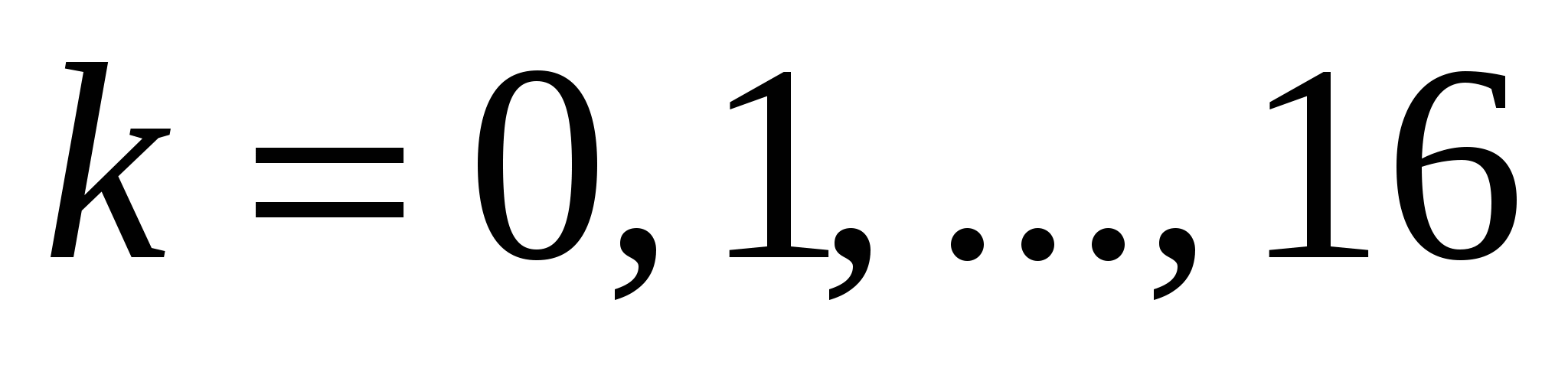 , принадлежащих области определения функции , принадлежащих области определения функции 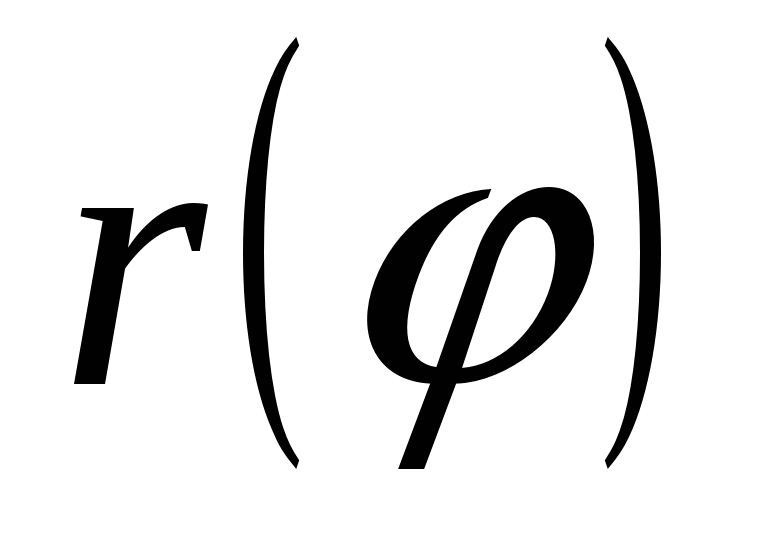 ; ;
найти уравнение данной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом в ПСК, а положительная полуось 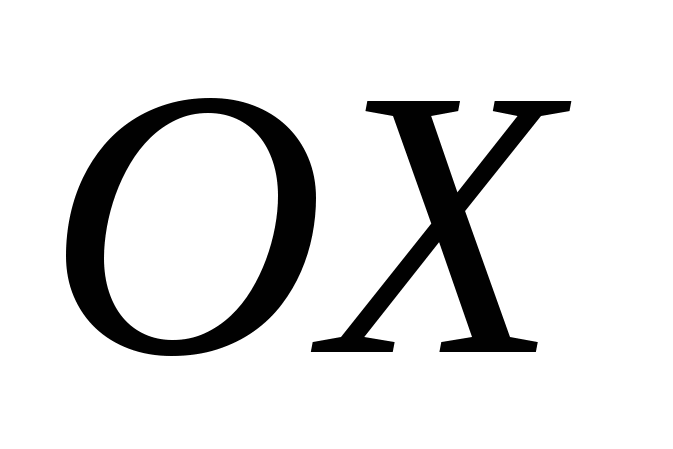 - с полярной осью - с полярной осью 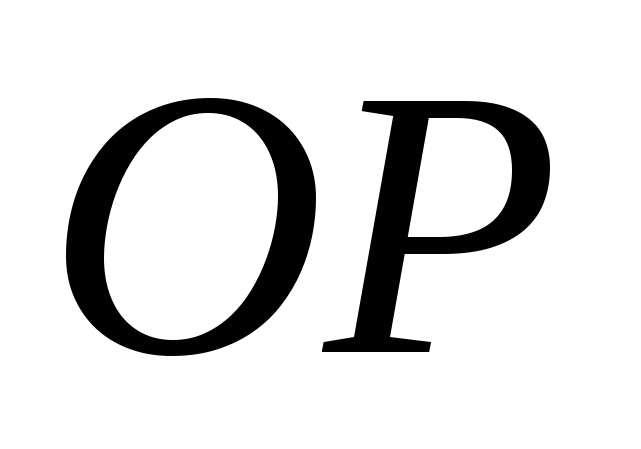 ; ;
определить тип кривой.
Решение
Область определения функции 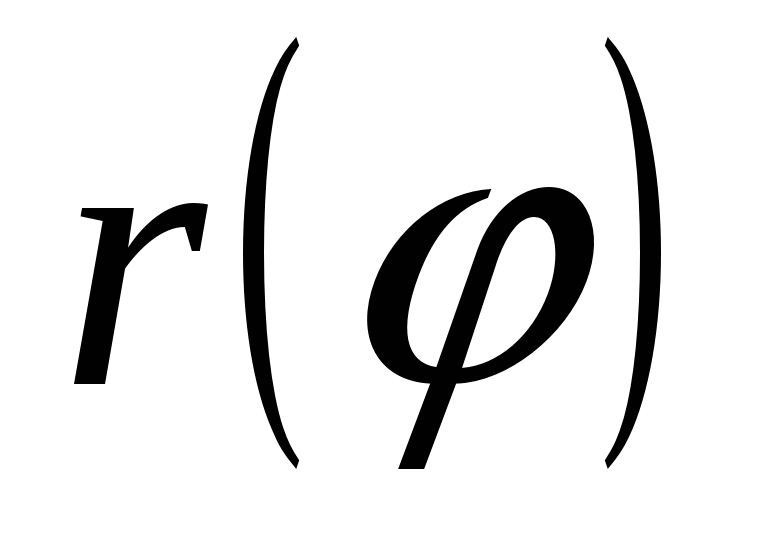 найдем из условия найдем из условия 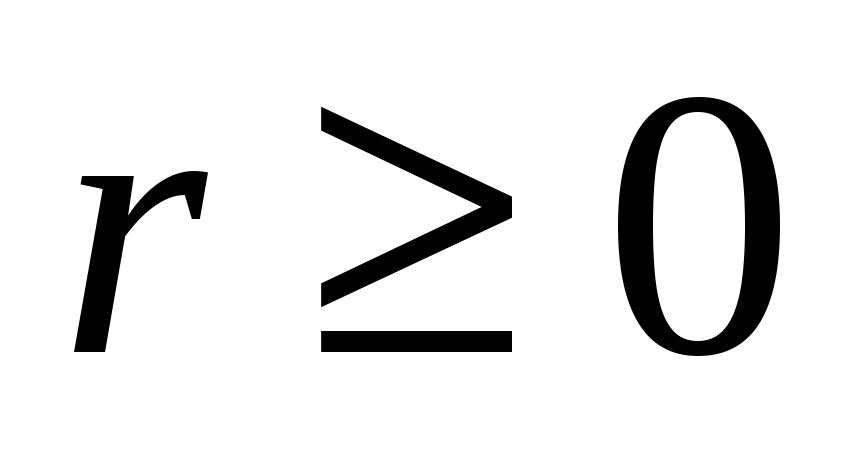 : :
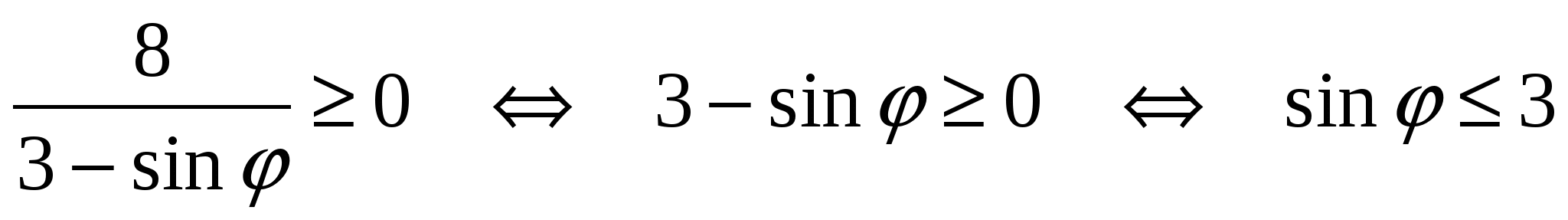
Последнее неравенство выполняется при любом  . Следовательно, область определения . Следовательно, область определения 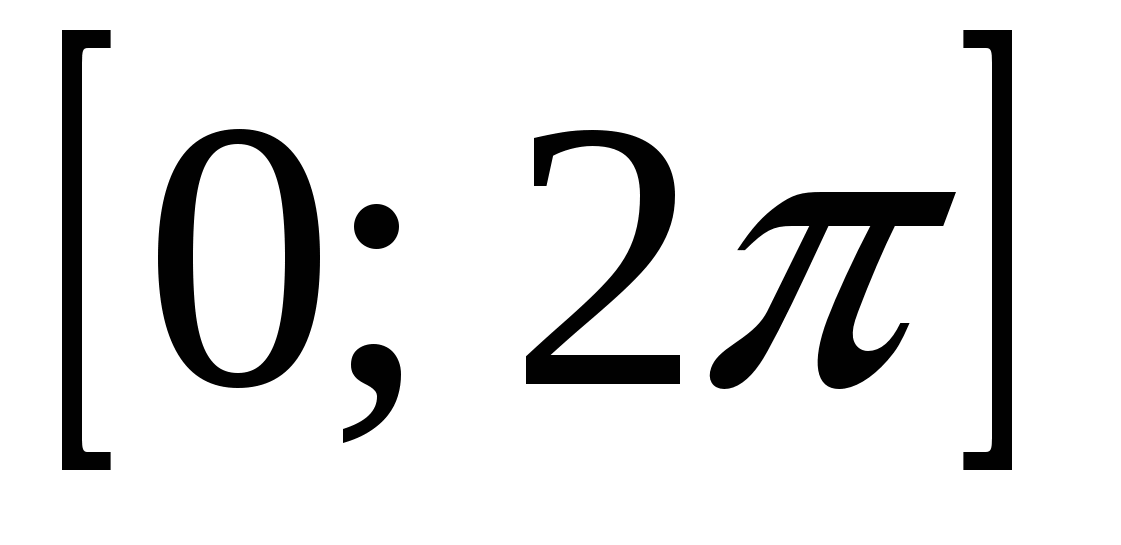
Для построения кривой в ПСК вычислим значения функции 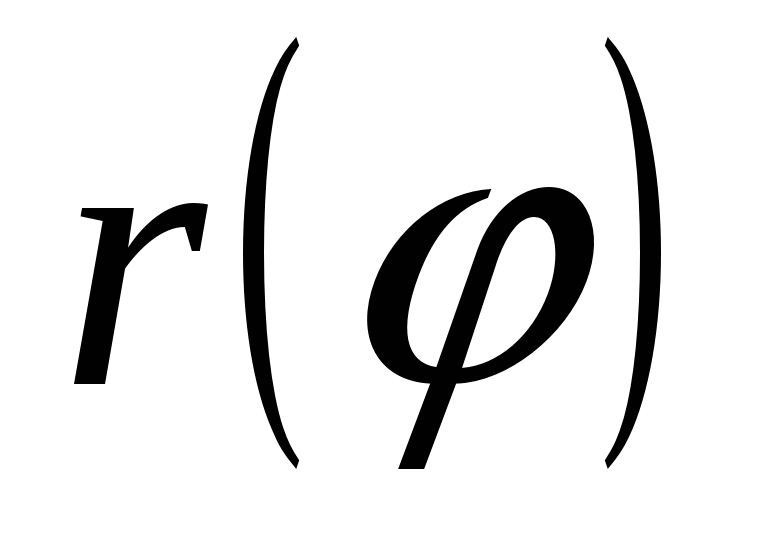 в точках в точках 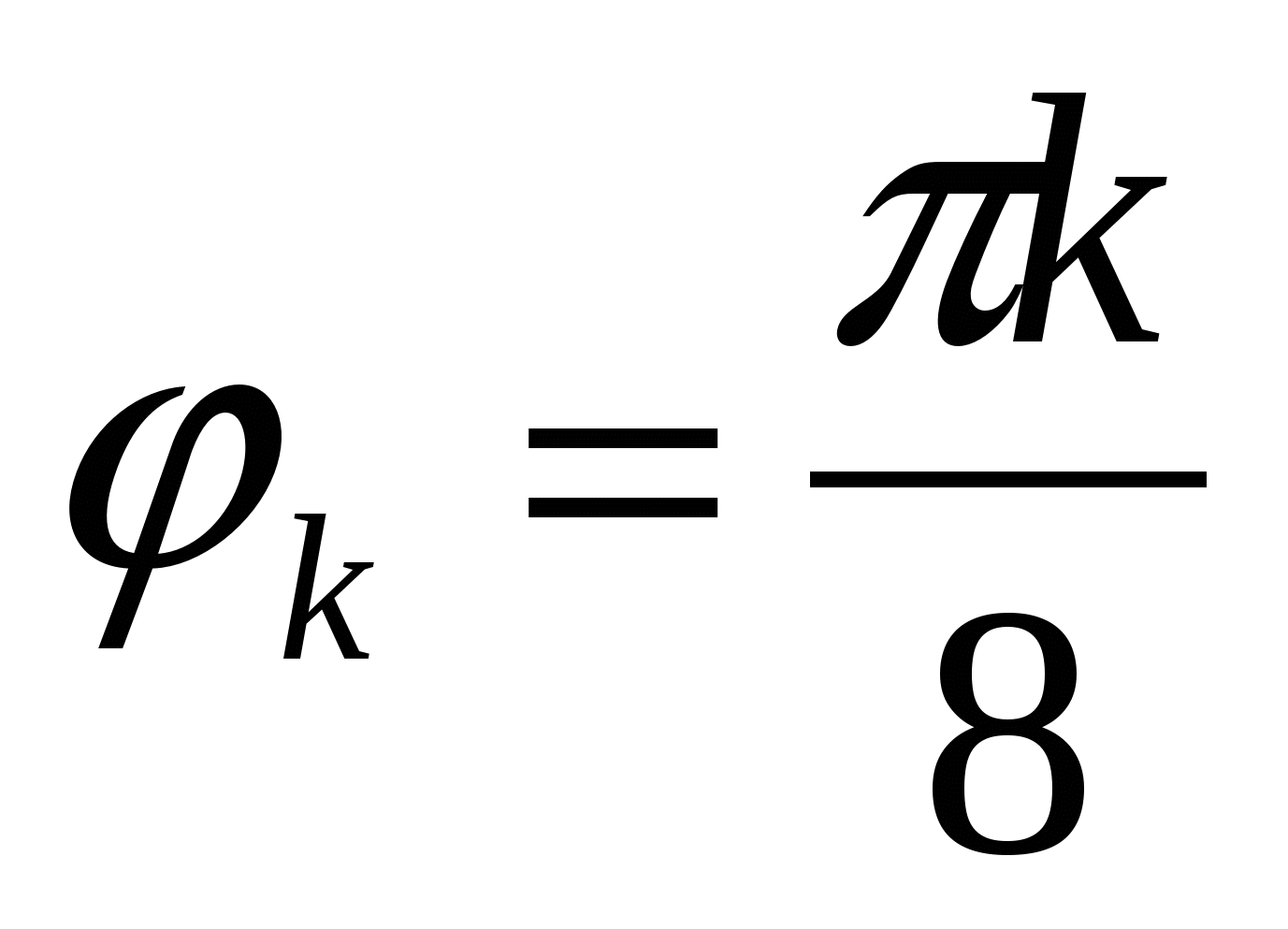 , , 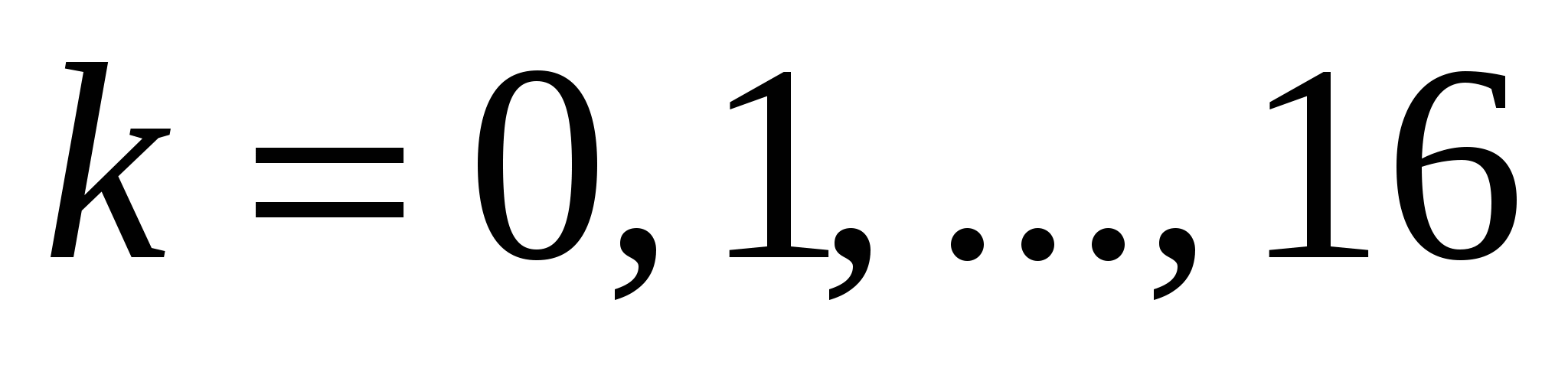 , входящих в область определения. , входящих в область определения.
-
|
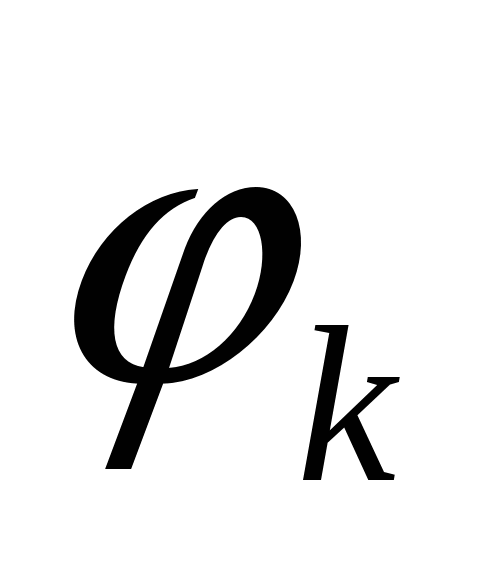
|
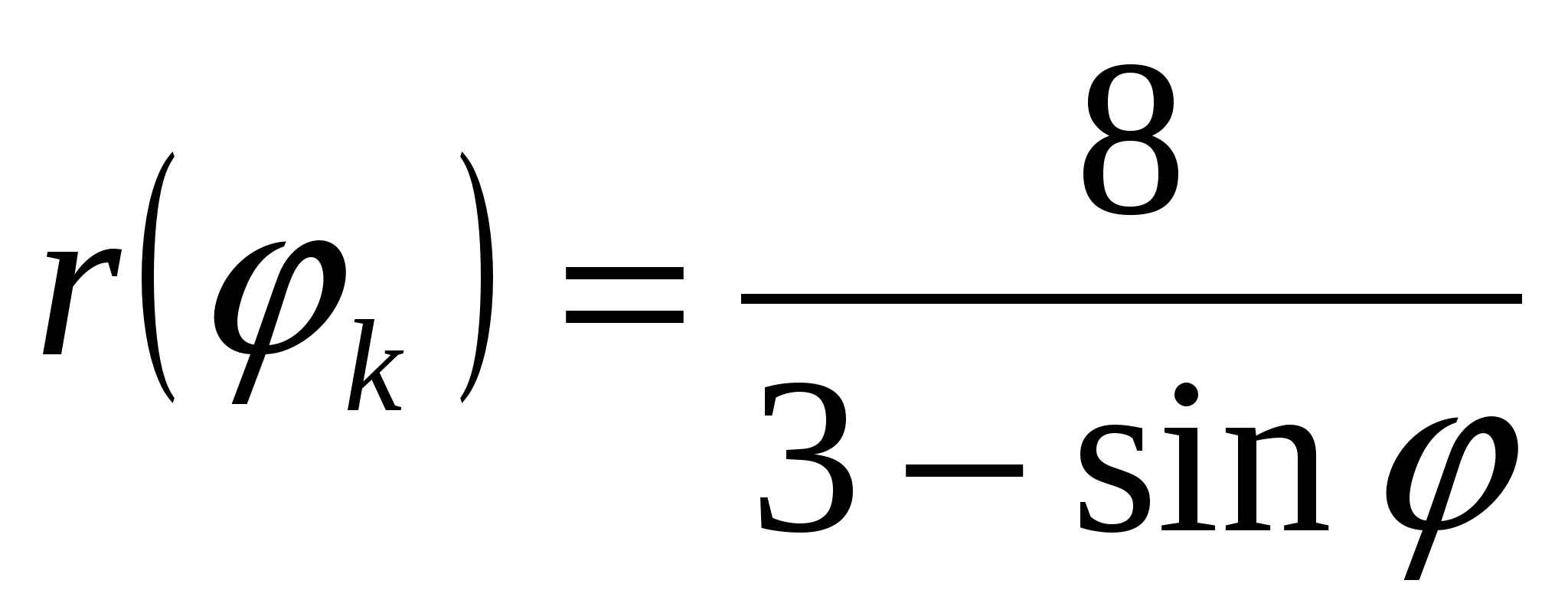
|
|
|
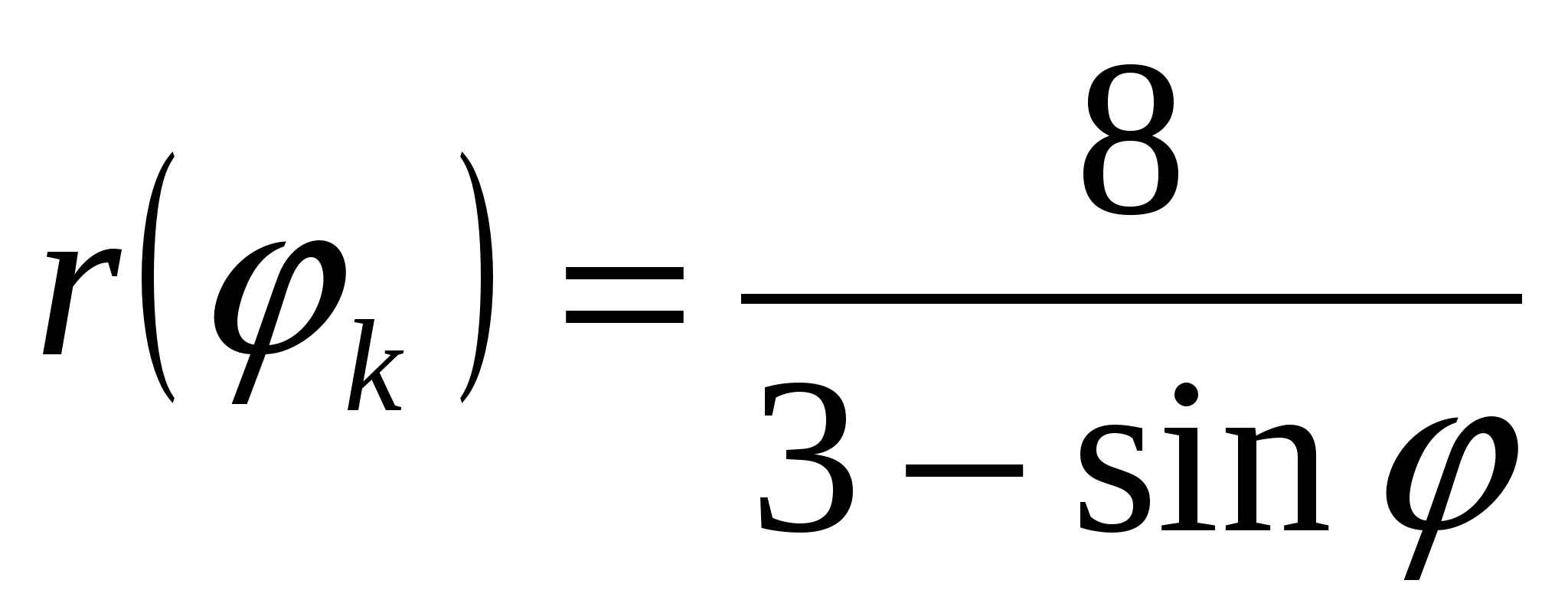
|
0
|
0
|
2,67
|
—
|
—
|
—
|
1
|
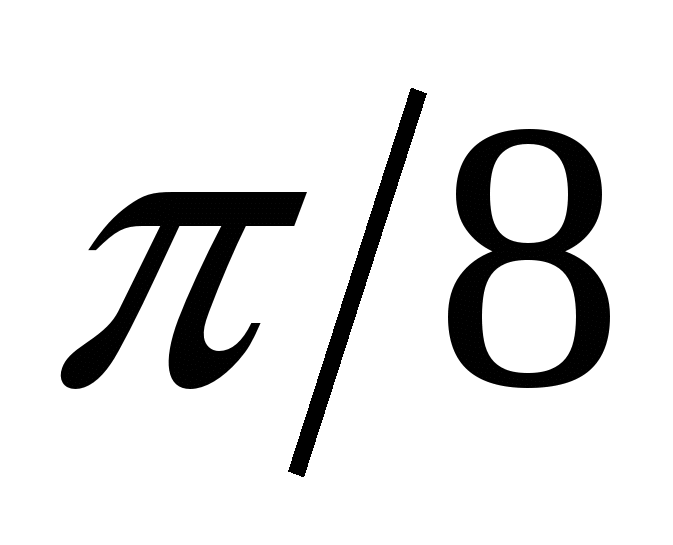
|
3,06
|
9
|
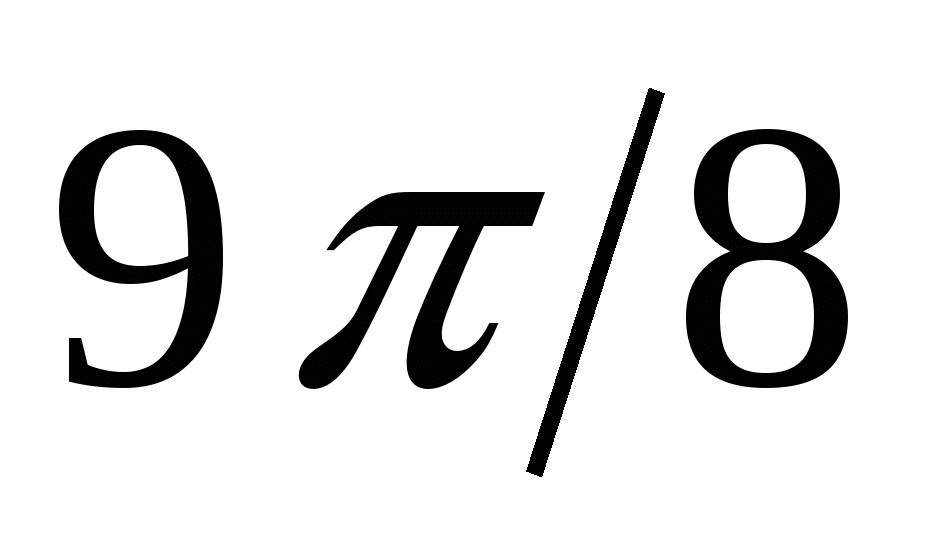
|
2,36
|
2
|

|
3,49
|
10
|
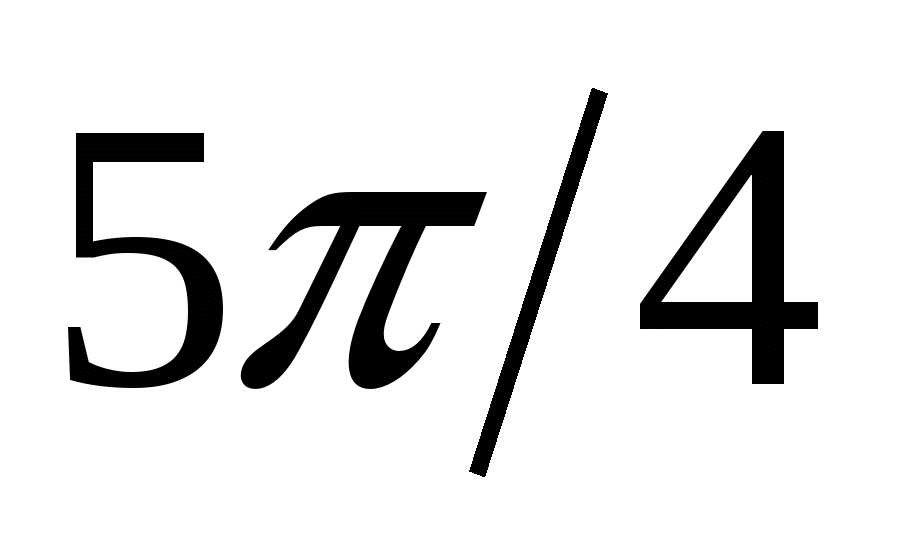
|
2,16
|
3
|
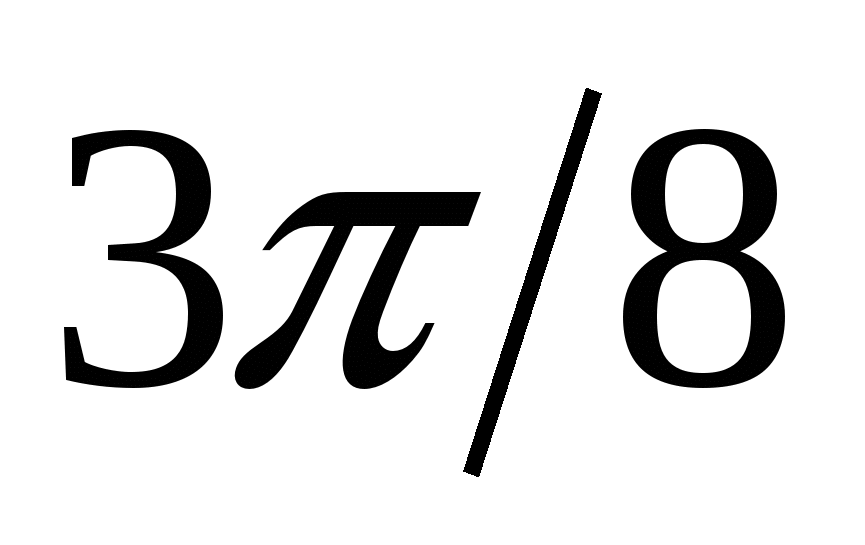
|
3,85
|
11
|
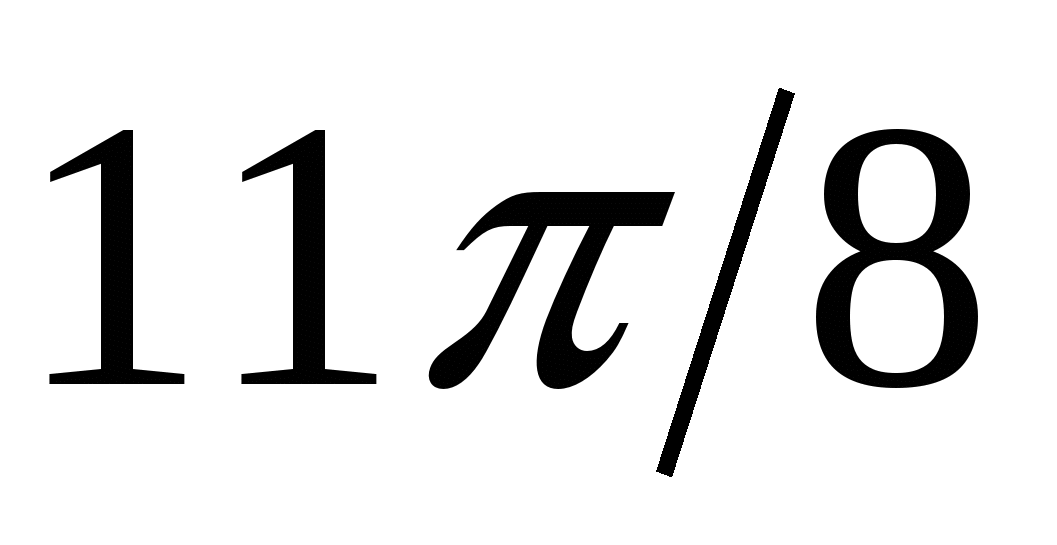
|
2,04
|
4
|
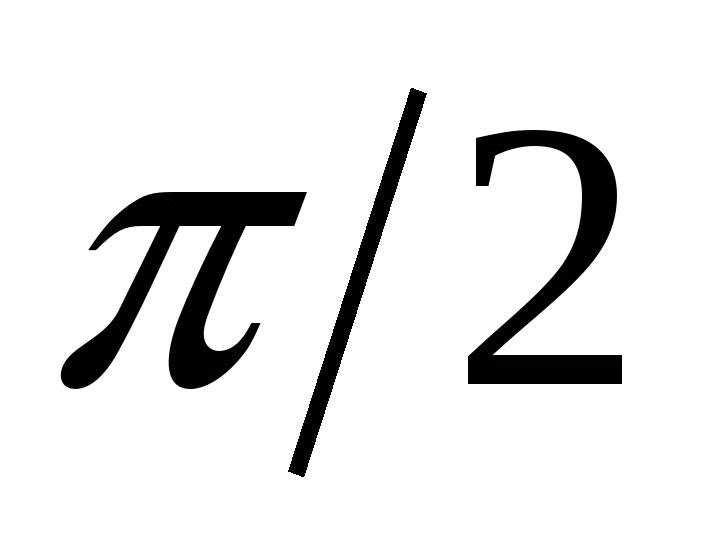
|
4,00
|
12
|
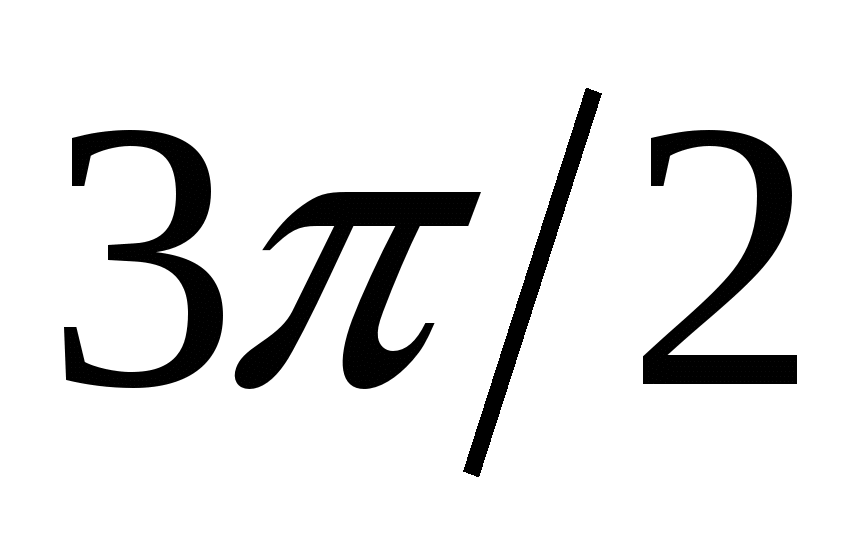
|
2,00
|
5
|
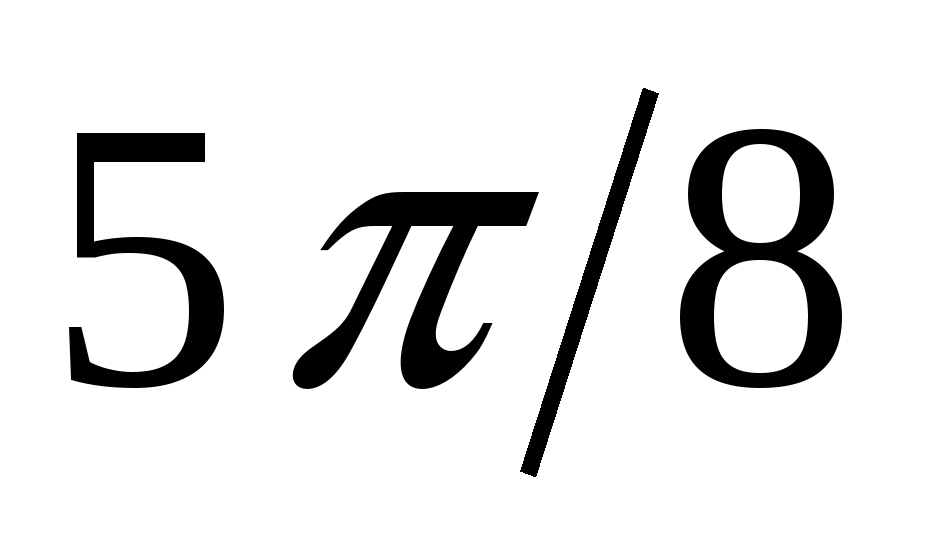
|
3,85
|
13
|

|
2,04
|
6
|
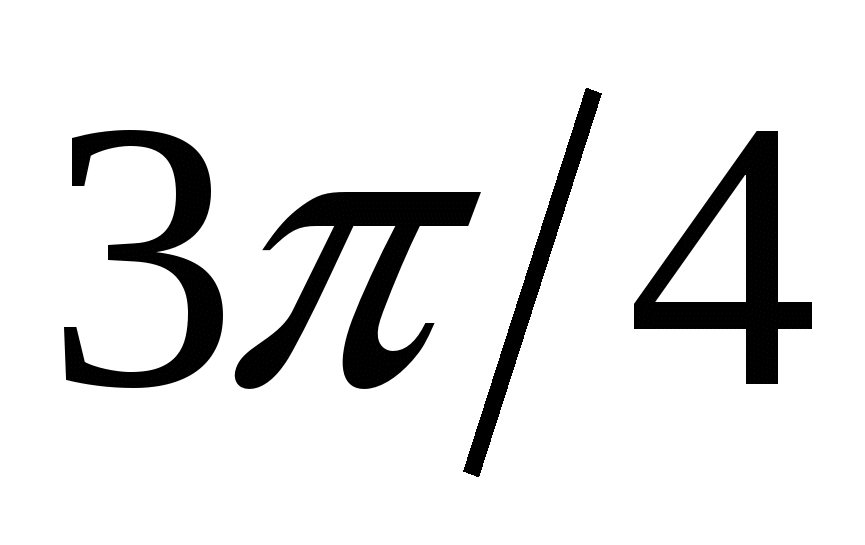
|
3,49
|
14
|
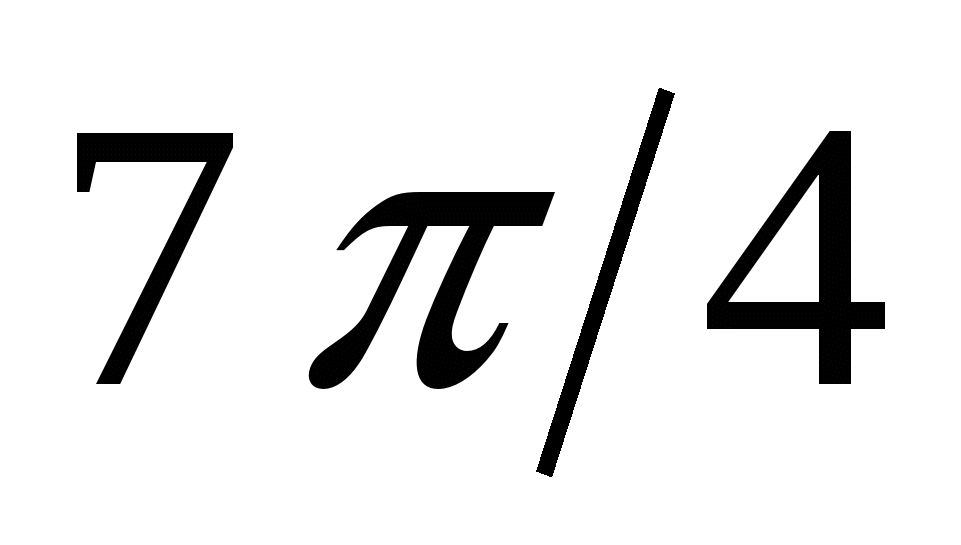
|
2,16
|
7
|
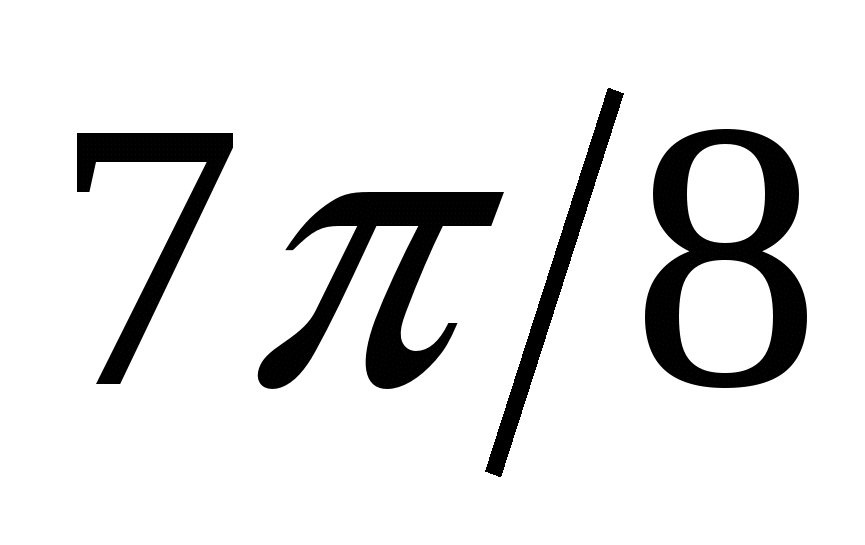
|
3,06
|
15
|
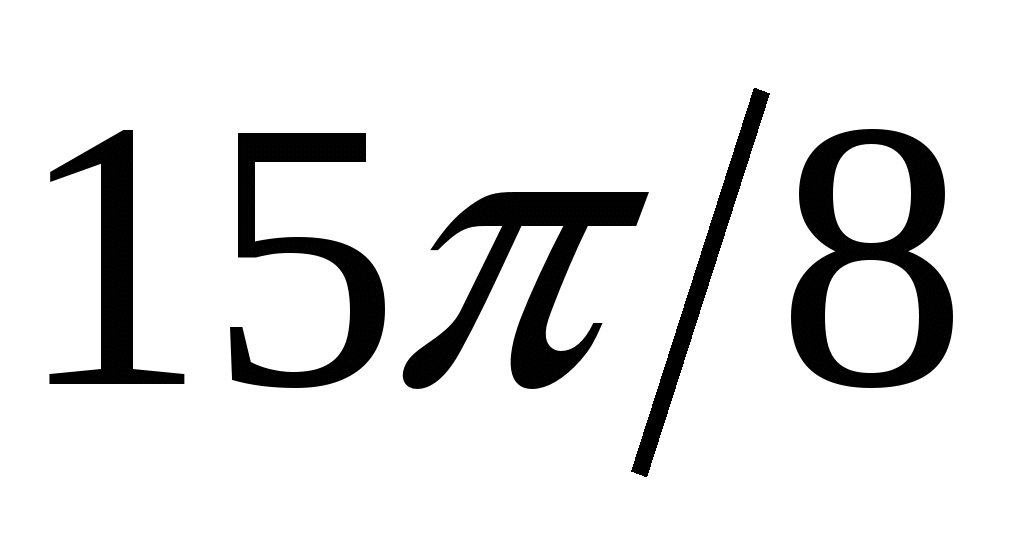
|
2,36
|
8
|

|
2,67
|
16
|
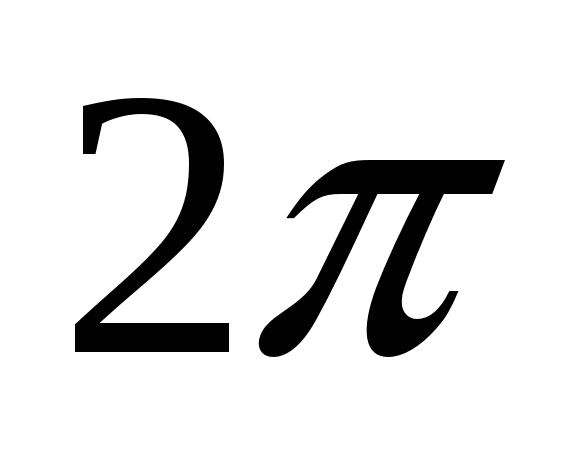
|
2,67
|
Найдем уравнение кривой, заданной в ПСК уравнением 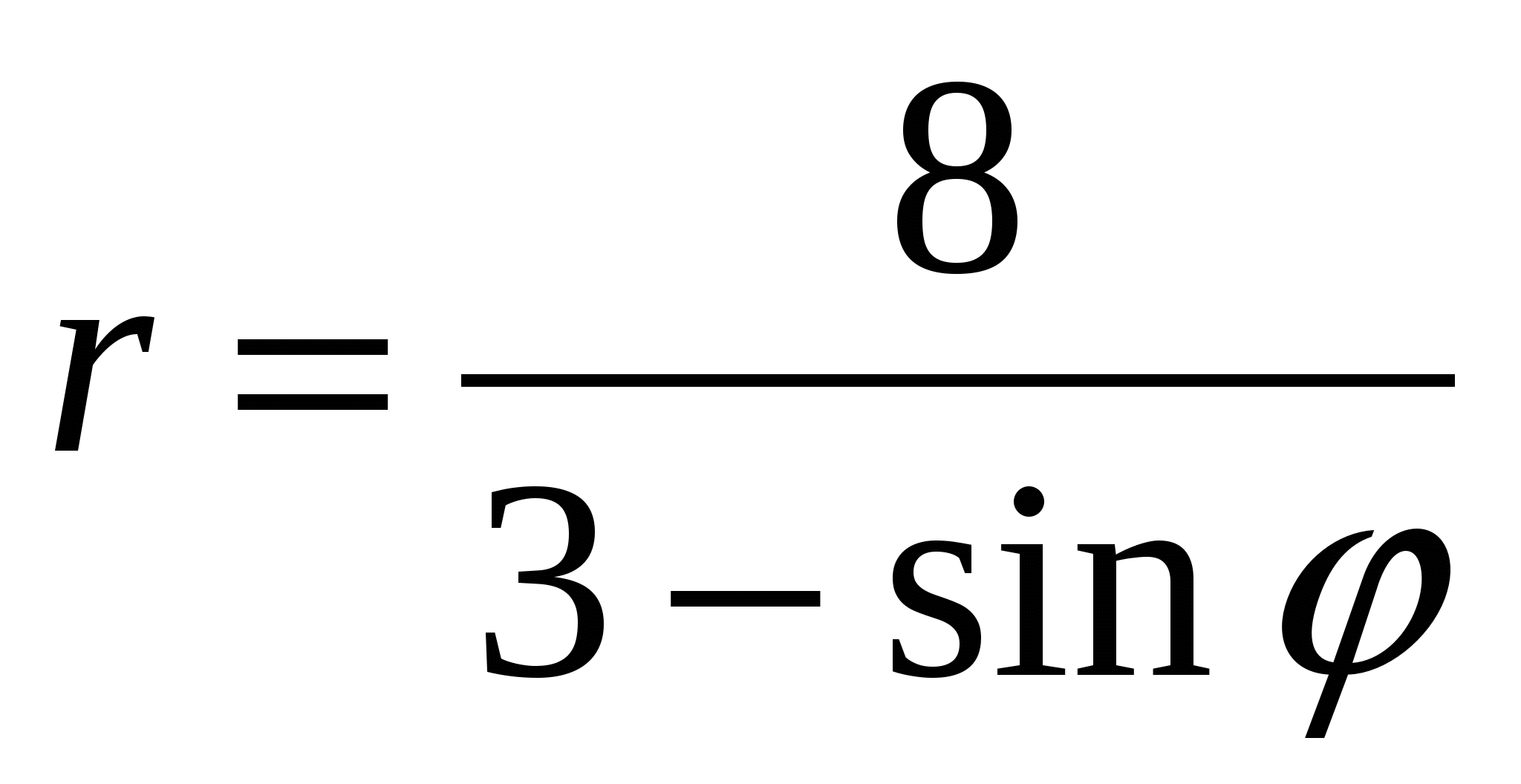 , в декартовой системе координат. , в декартовой системе координат.
Если совместить ПСК и ДСК так, чтобы полюс совпал с началом координат ДСК, а ось  совпадала с положительной полуосью совпадала с положительной полуосью 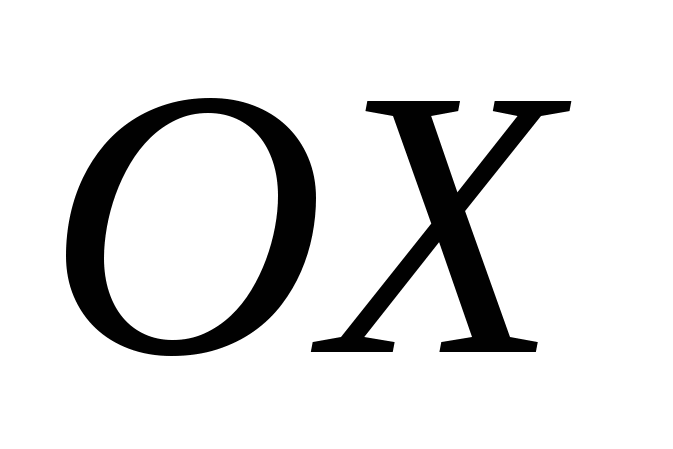 , то, используя формулы связи между декартовыми и полярными координатами точки , то, используя формулы связи между декартовыми и полярными координатами точки
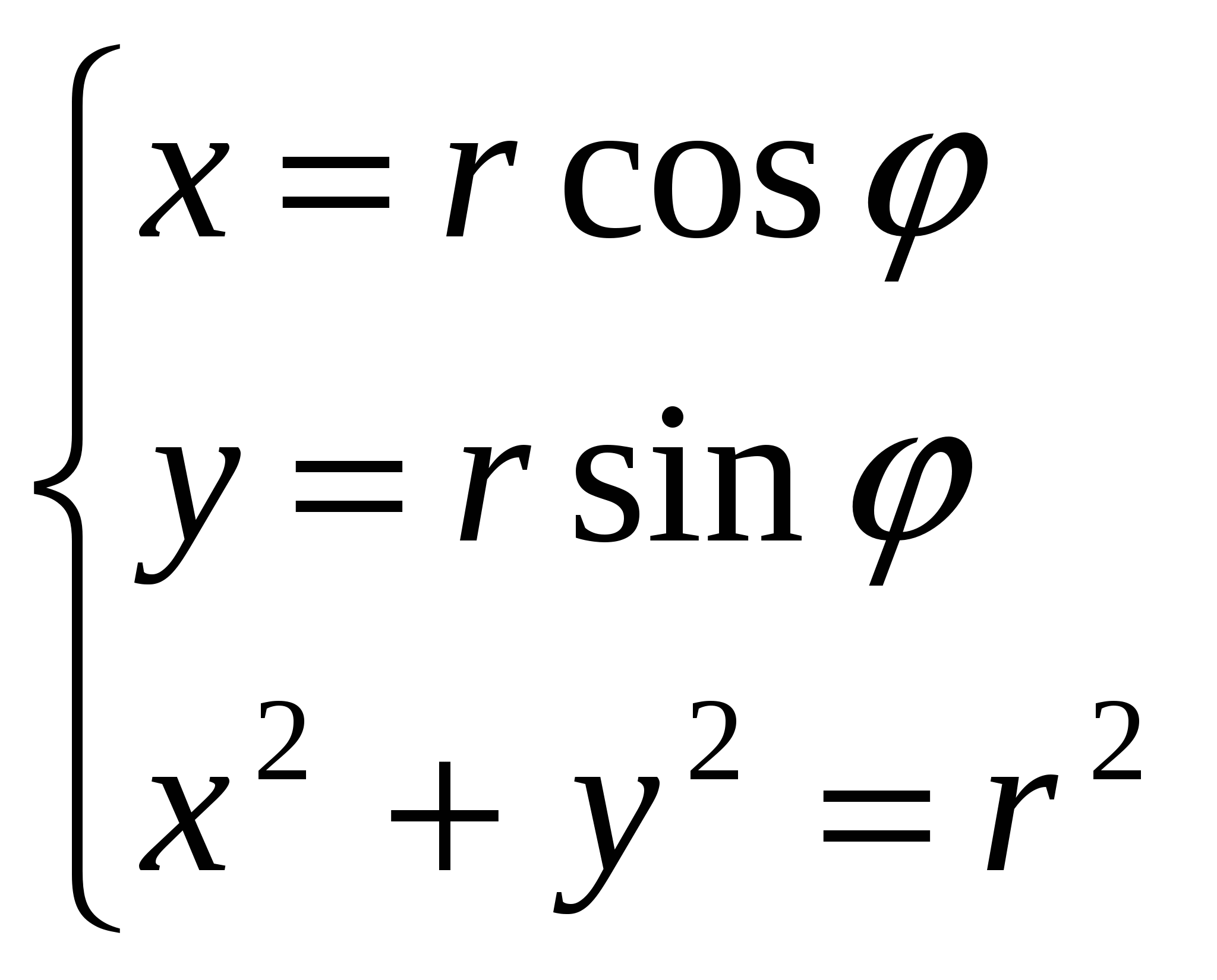 получим получим 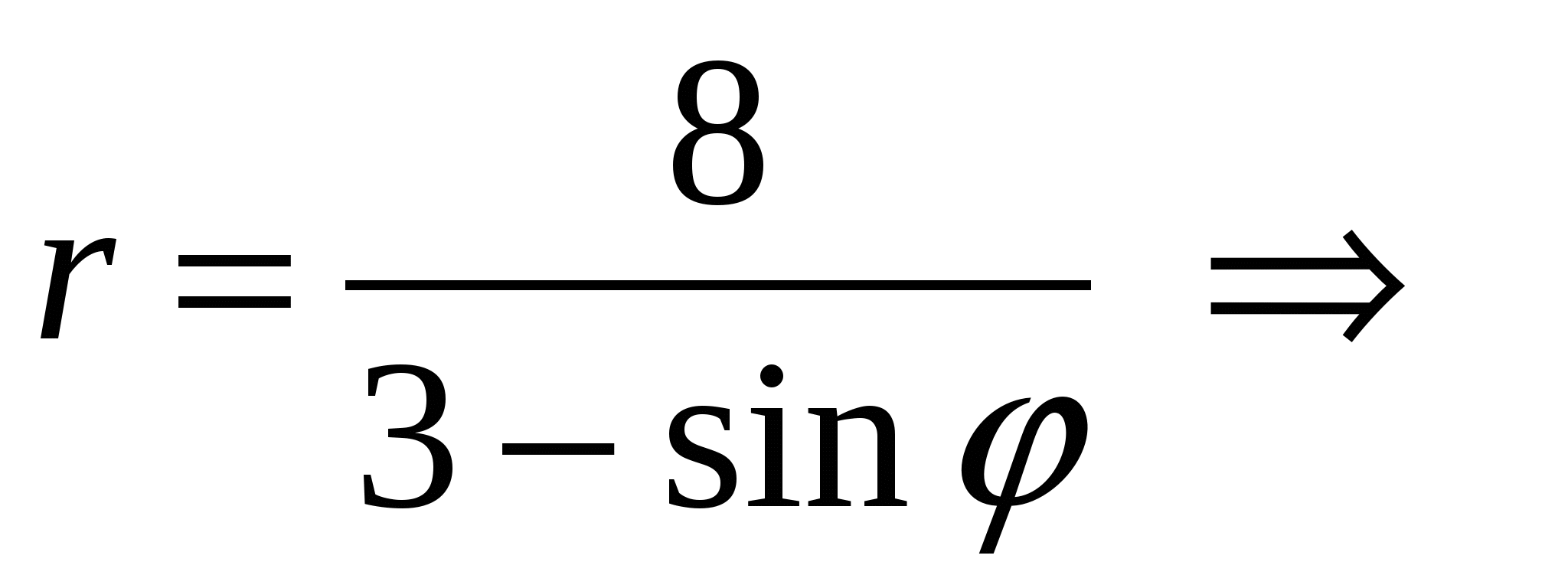 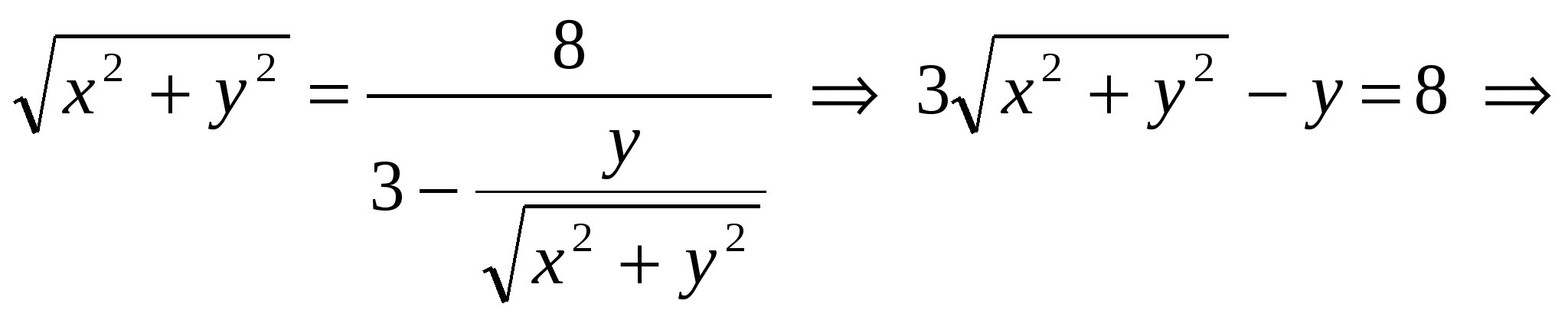
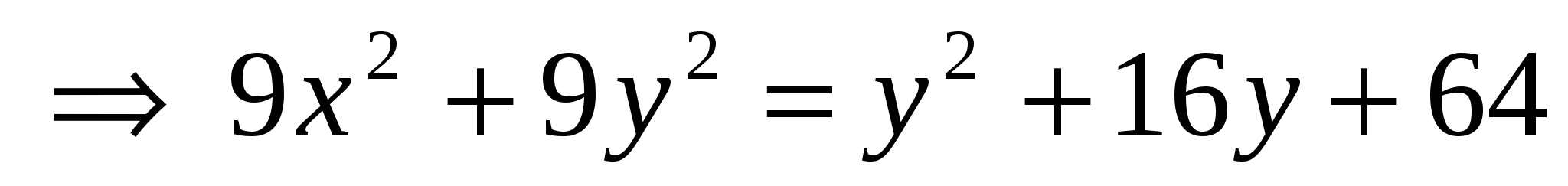 , ,
следовательно, уравнение кривой 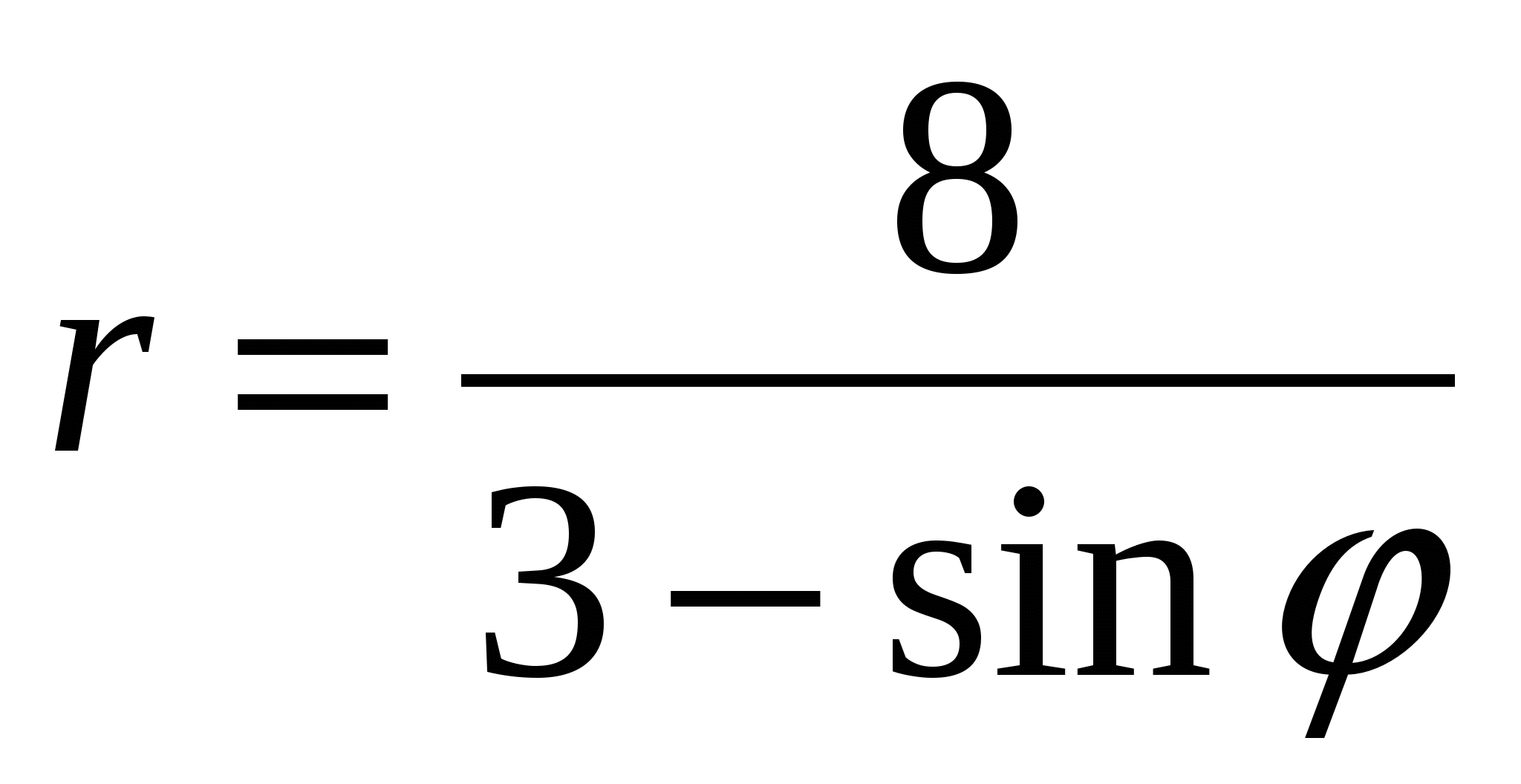 в ДСК имеет вид уравнения кривой второго порядка: в ДСК имеет вид уравнения кривой второго порядка: 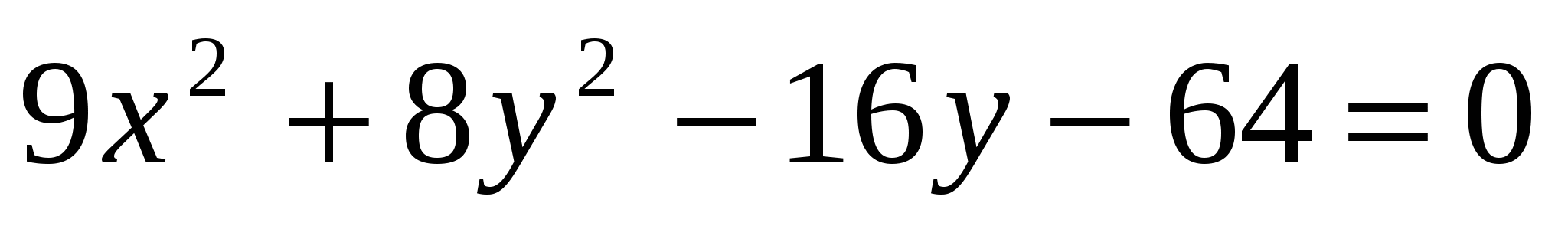
4) Для определения типа кривой выделим в уравнении полный квадрат по переменной 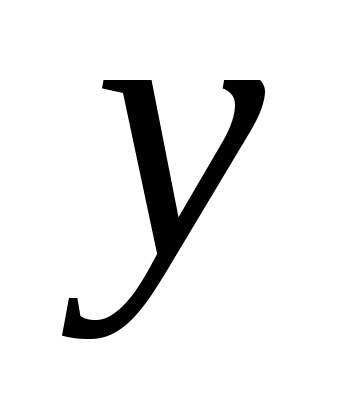 : :
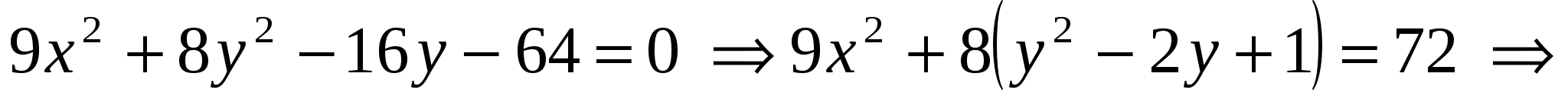 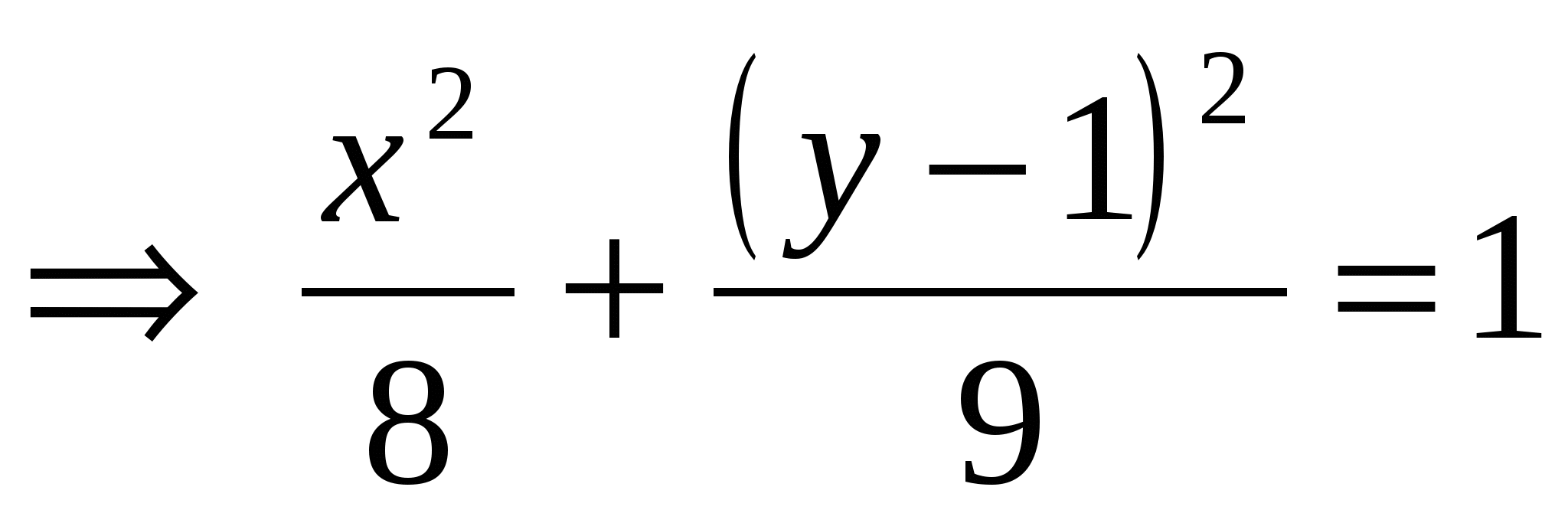
Это уравнение задает эллипс с центром в точке 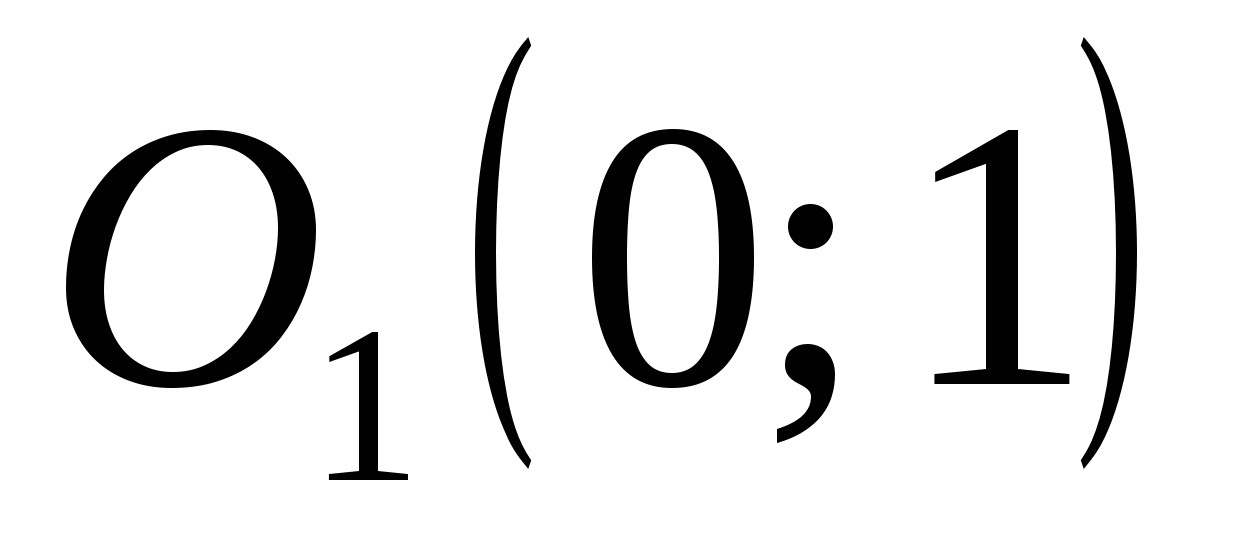 , с полуосями , с полуосями 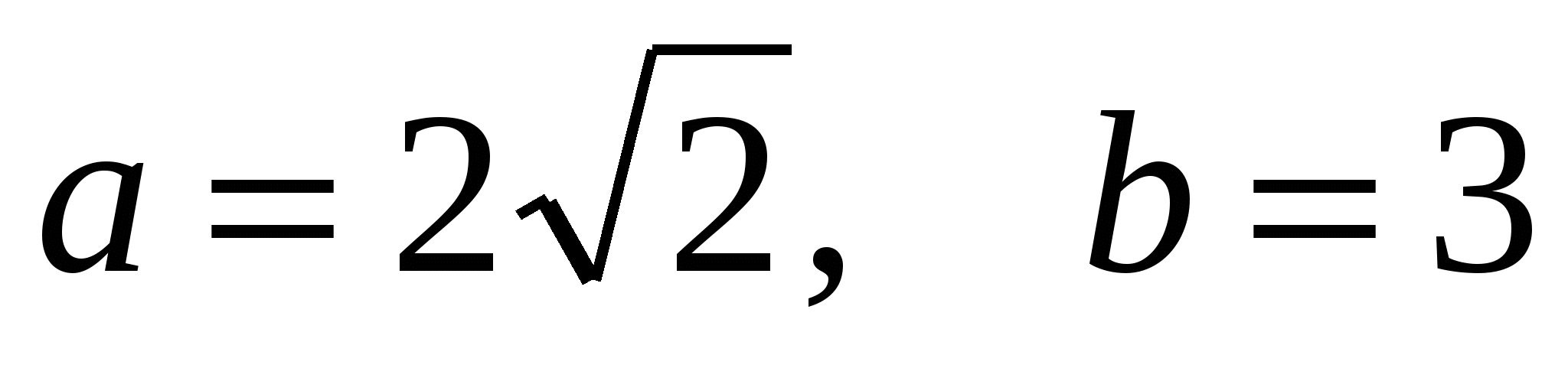 . Найдем координаты точки . Найдем координаты точки 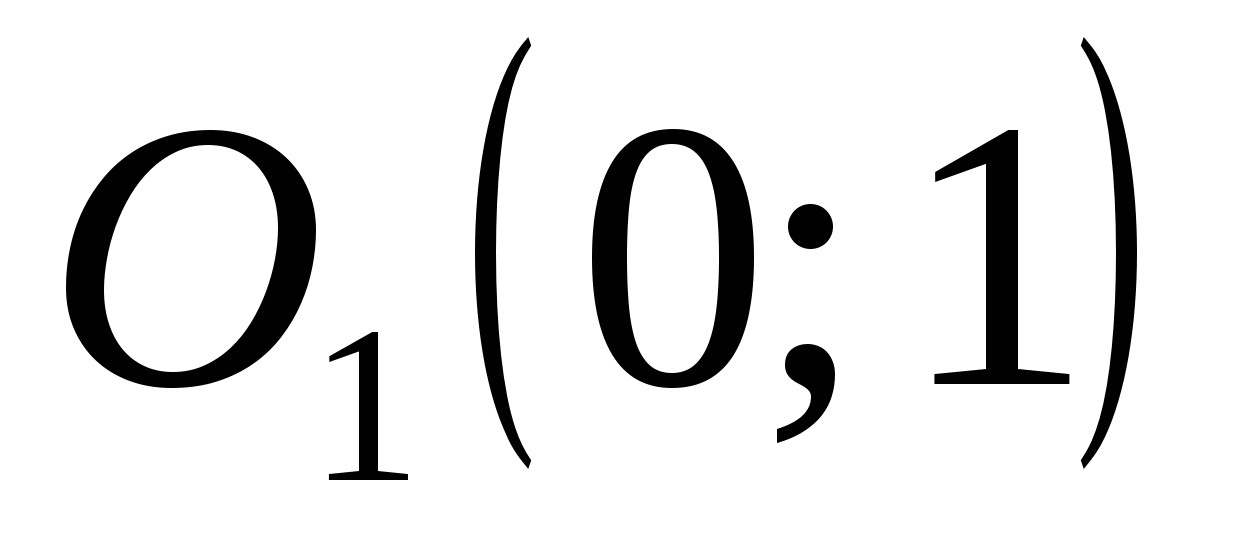 в ПСК: в ПСК:
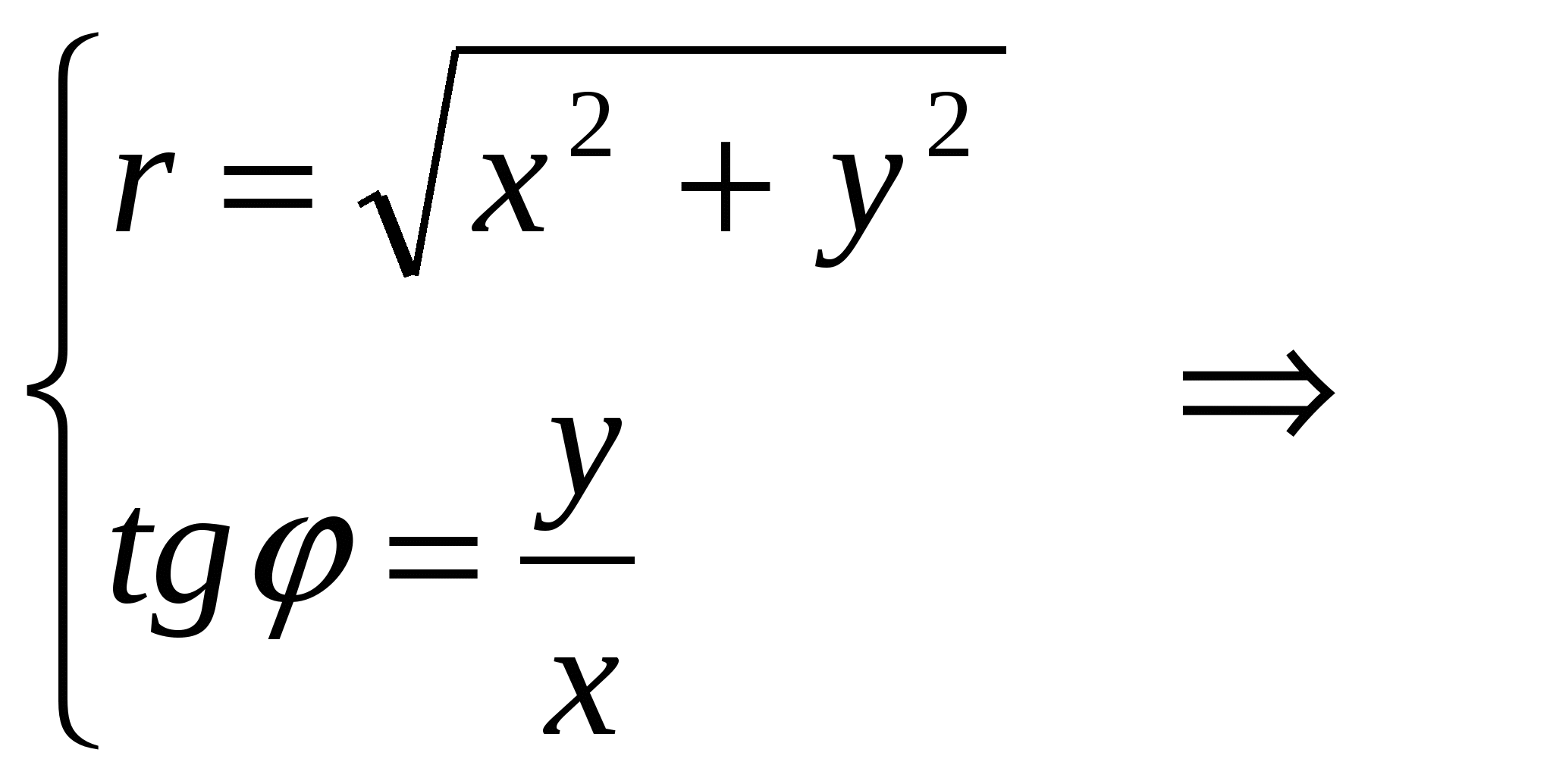 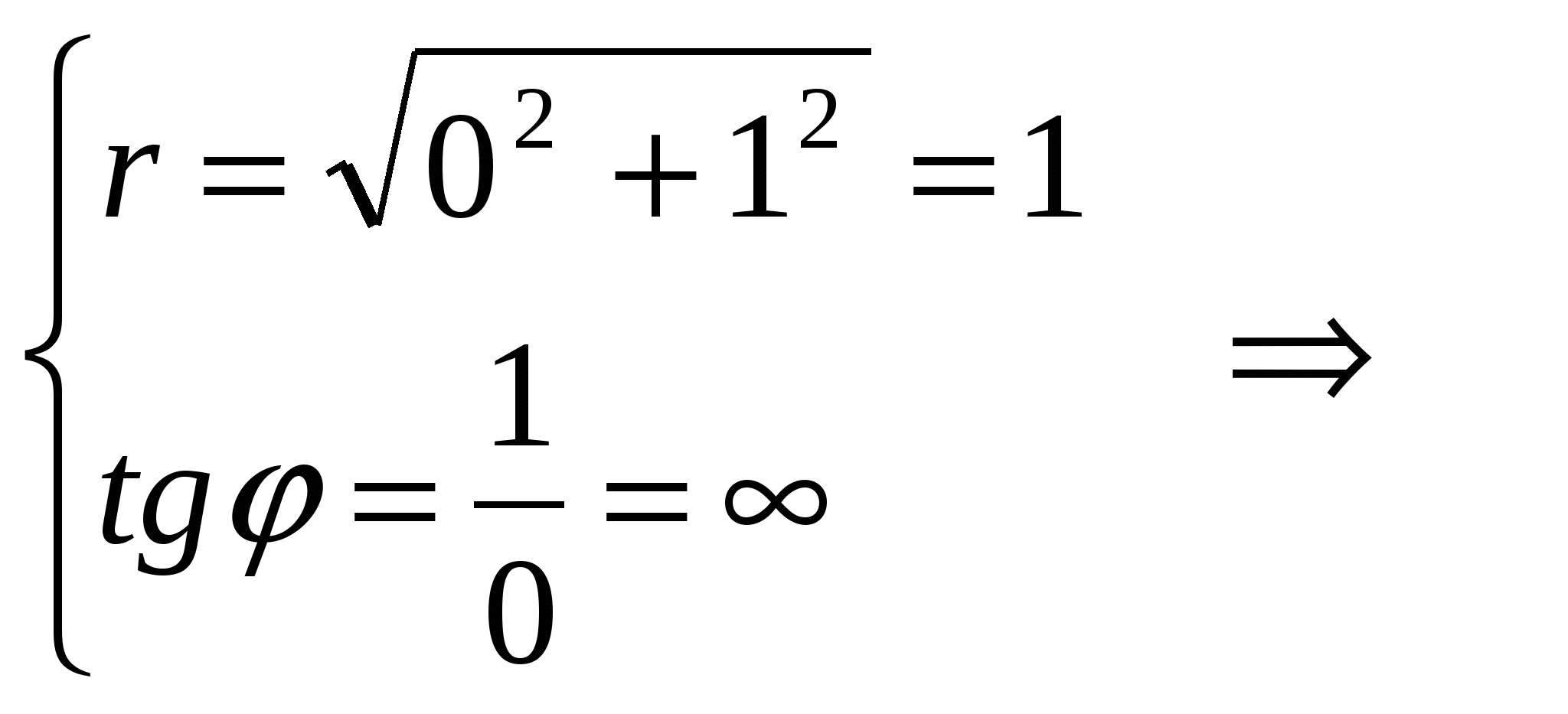 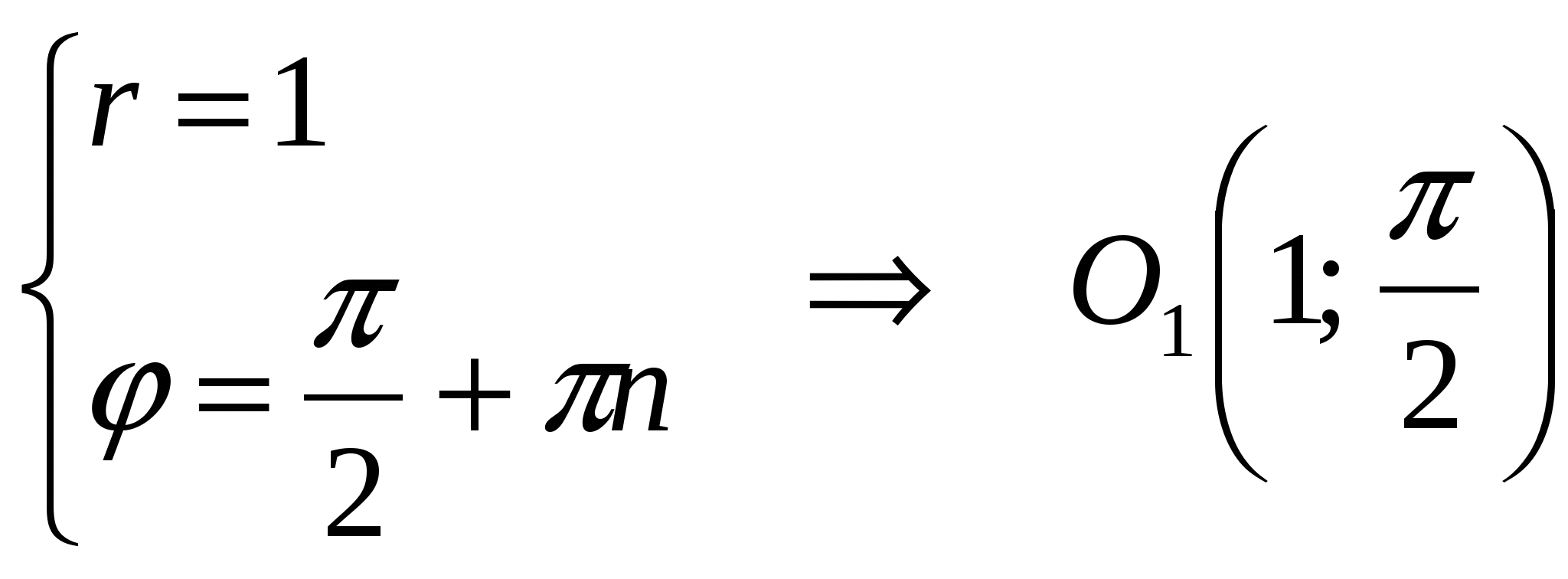
Ответы:
область определения: 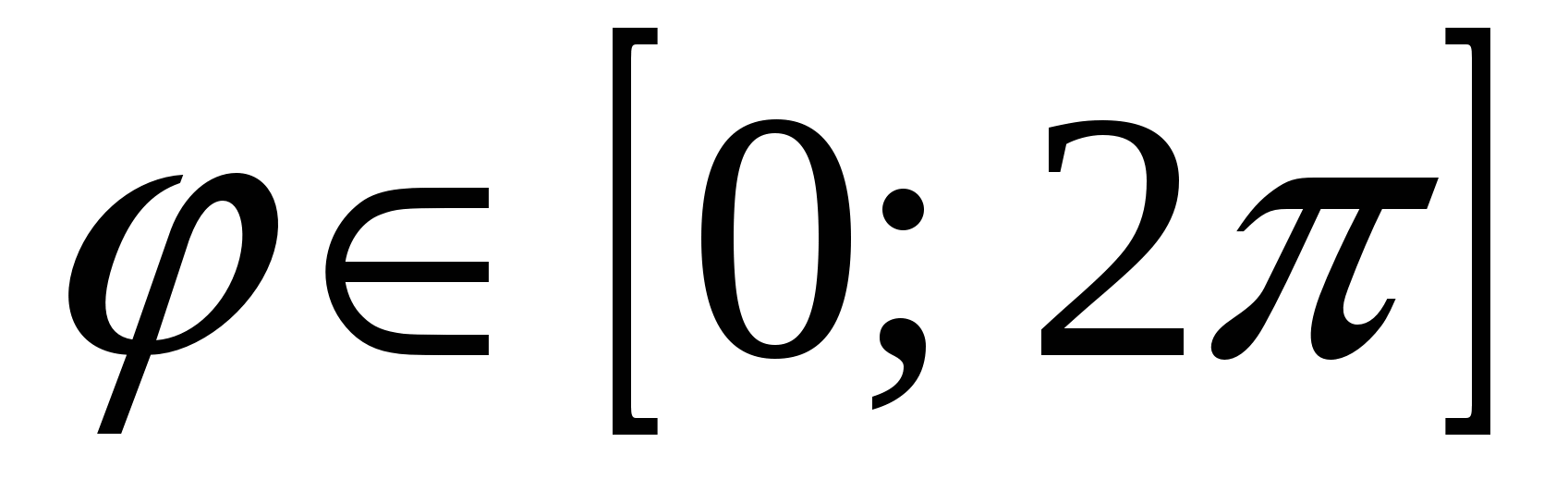 ; ;
чертеж выполнен
уравнение кривой в ДСК: 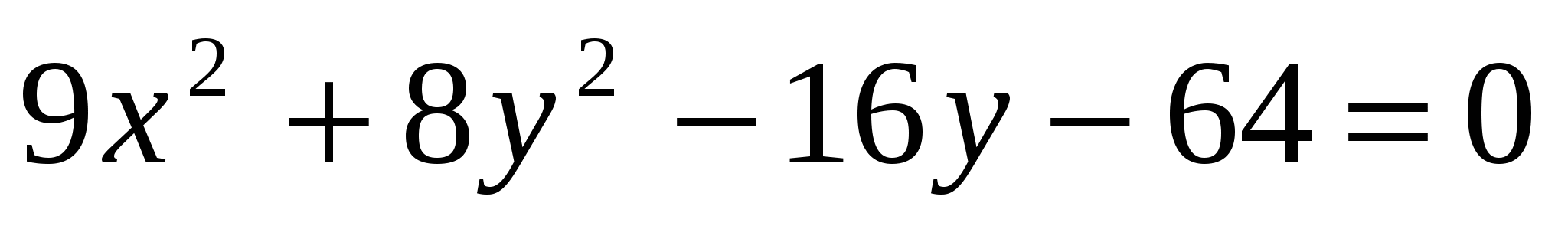 ; ;
тип кривой – эллипс с центром в точке 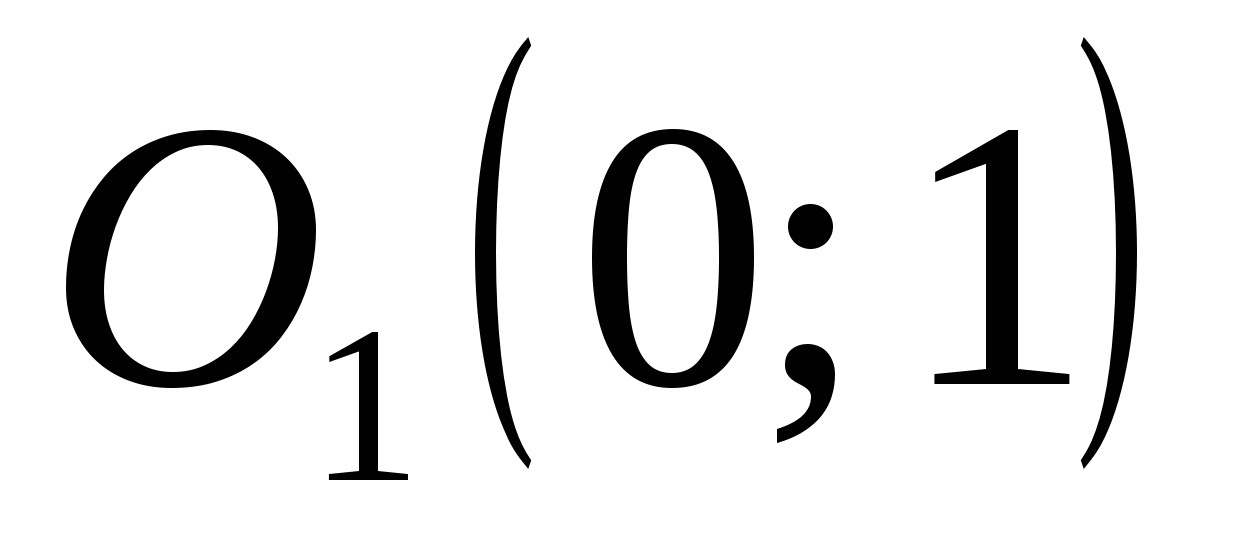 , с полуосями , с полуосями 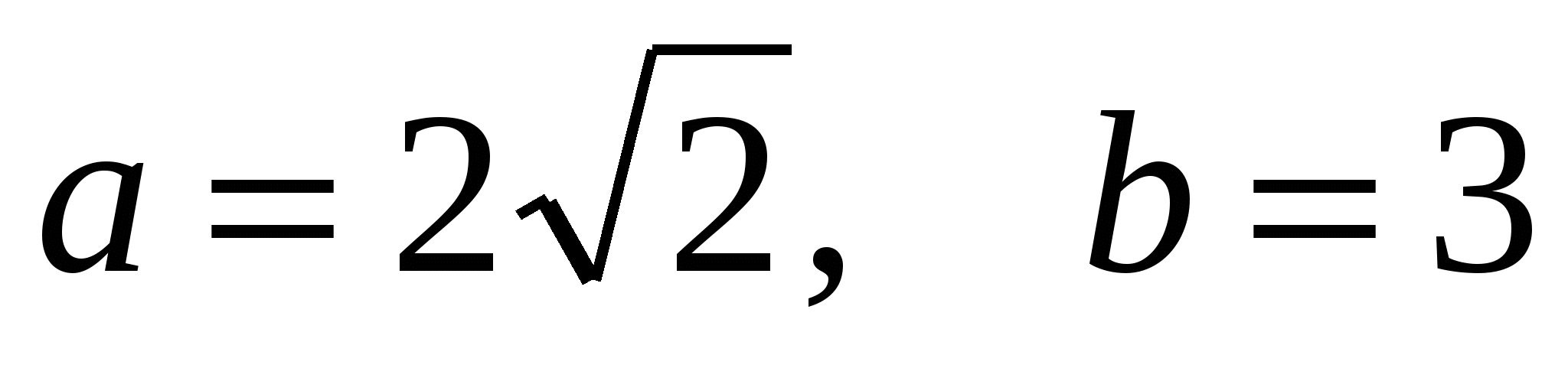 . .
|
 Скачать 408.5 Kb.
Скачать 408.5 Kb.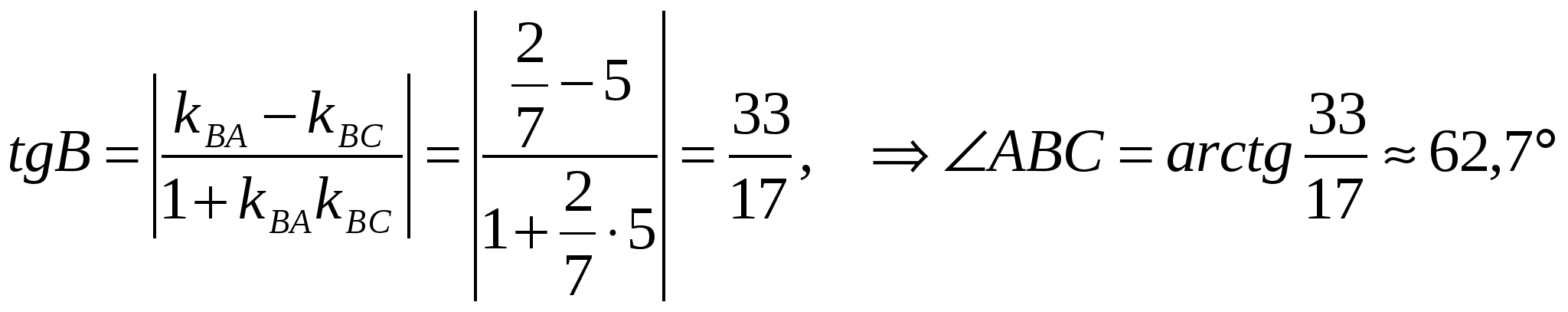


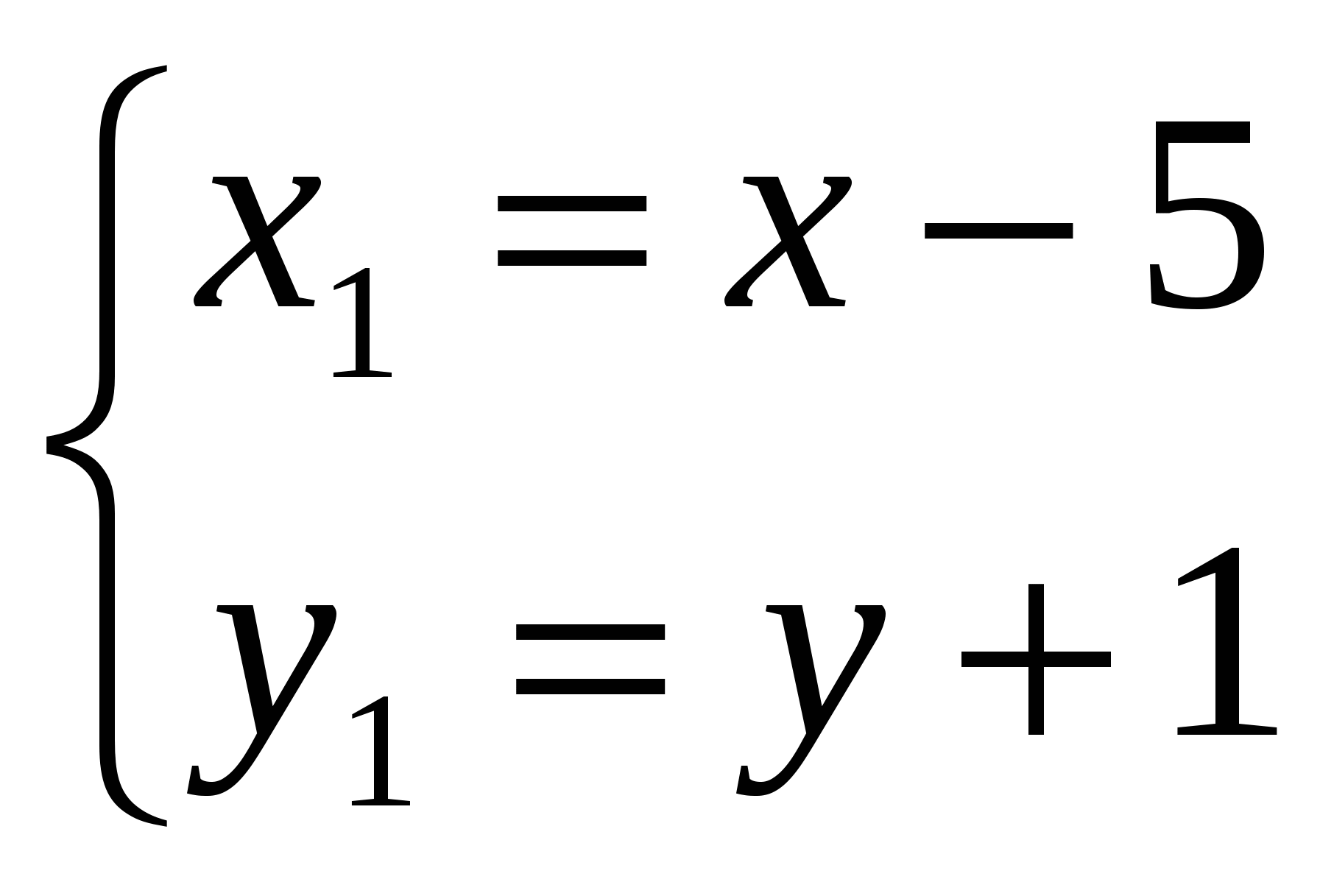 , получим каноническое уравнение гиперболы
, получим каноническое уравнение гиперболы 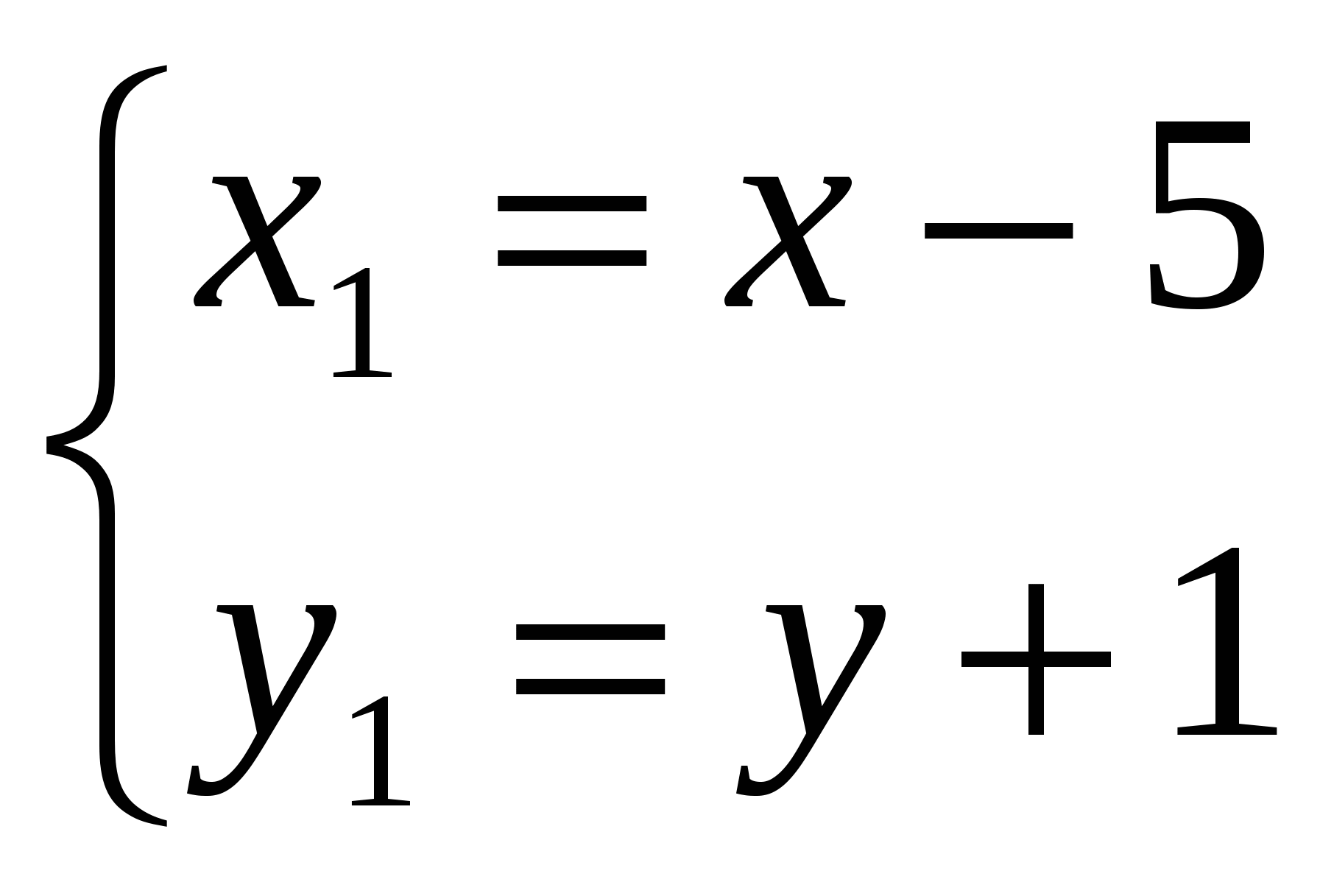 . Характерные элементы:
. Характерные элементы:
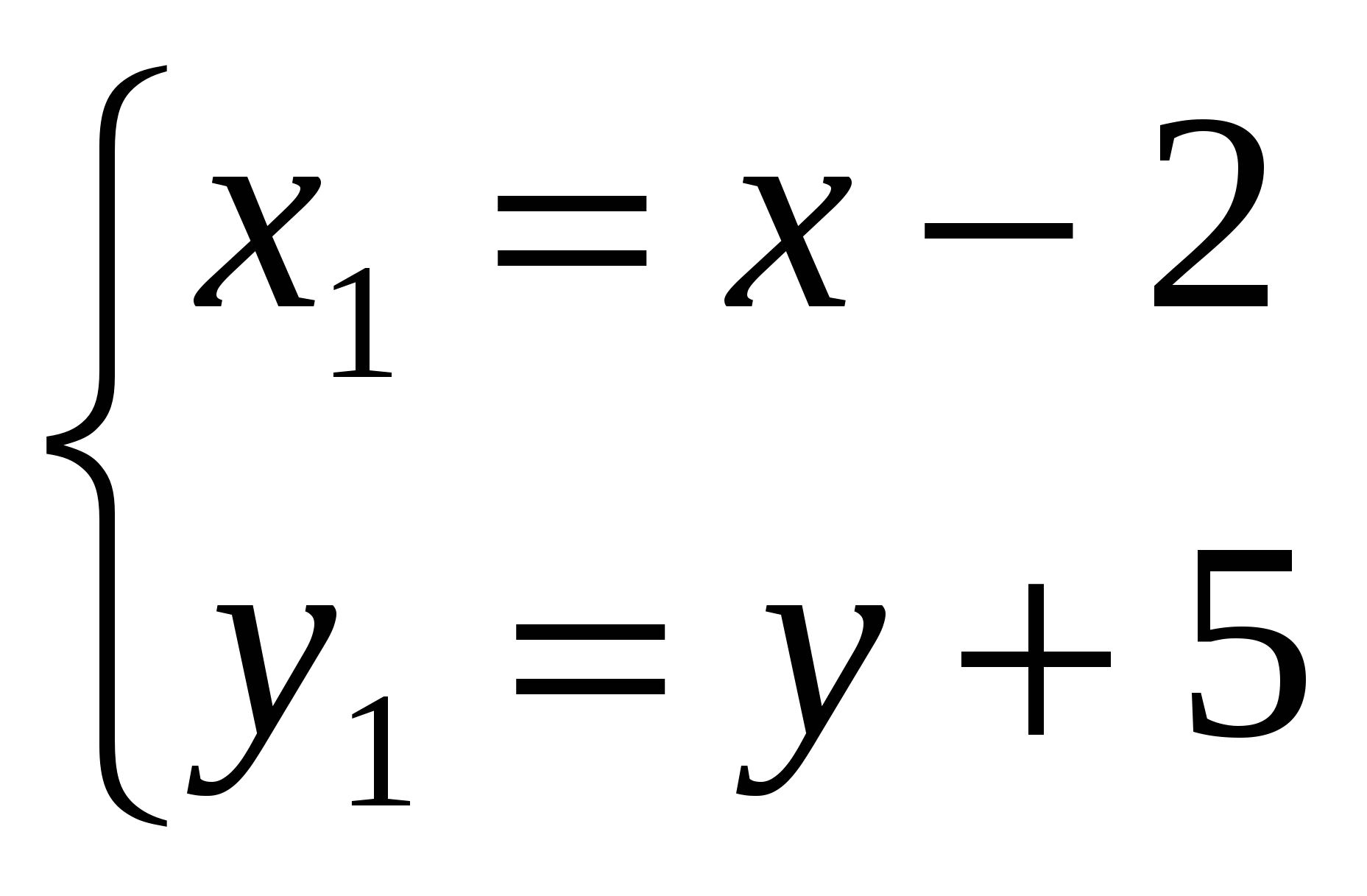 , получим каноническое уравнение гиперболы
, получим каноническое уравнение гиперболы 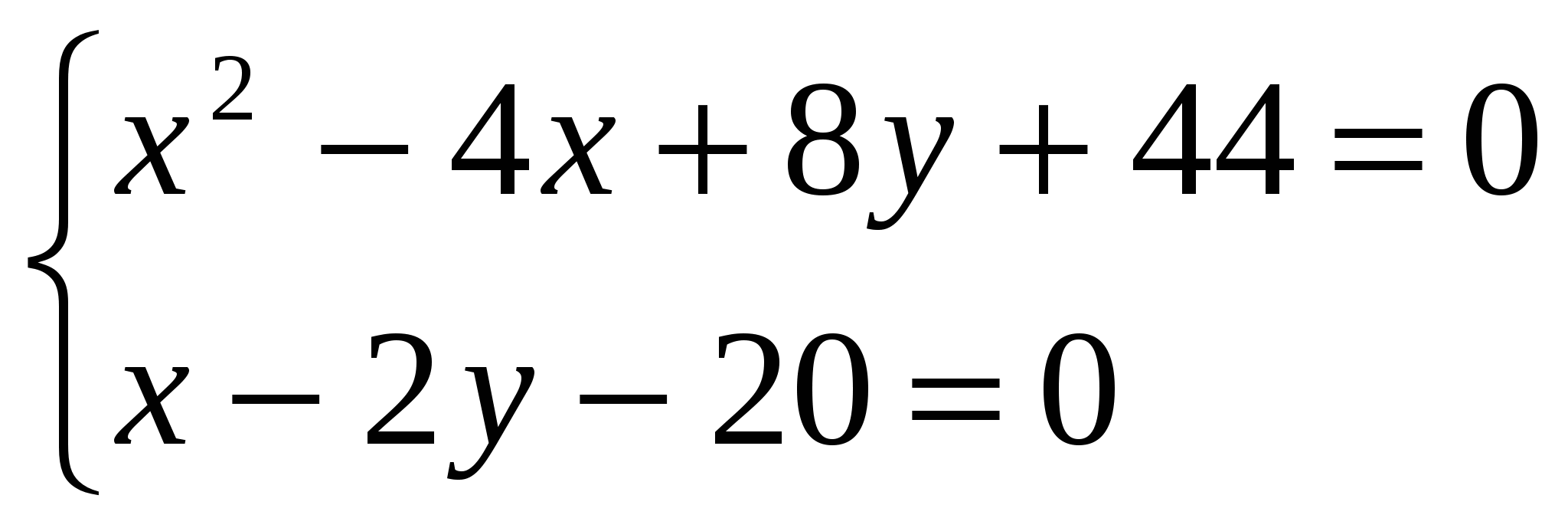
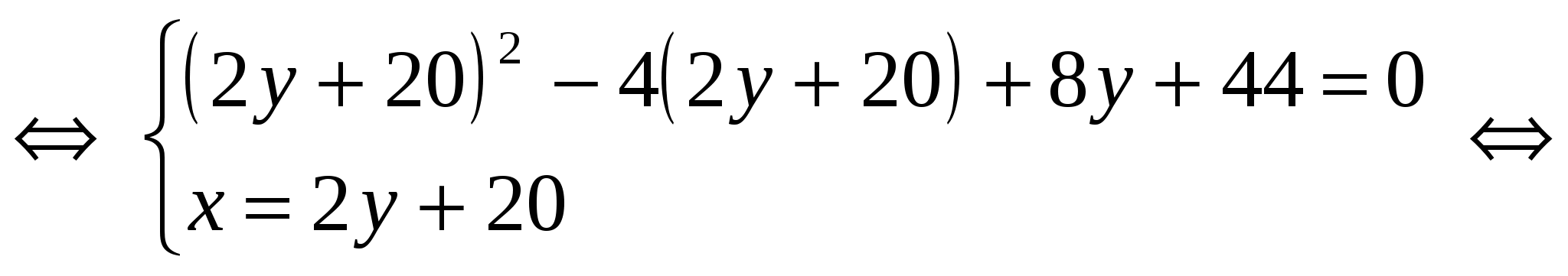
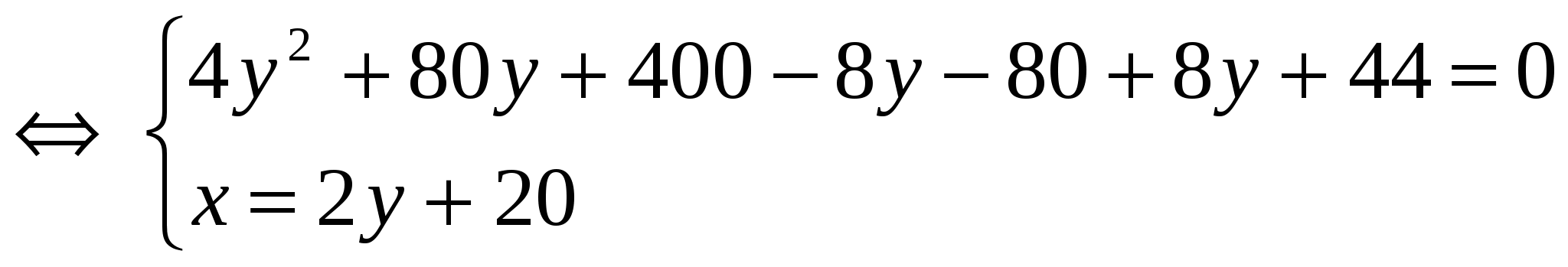
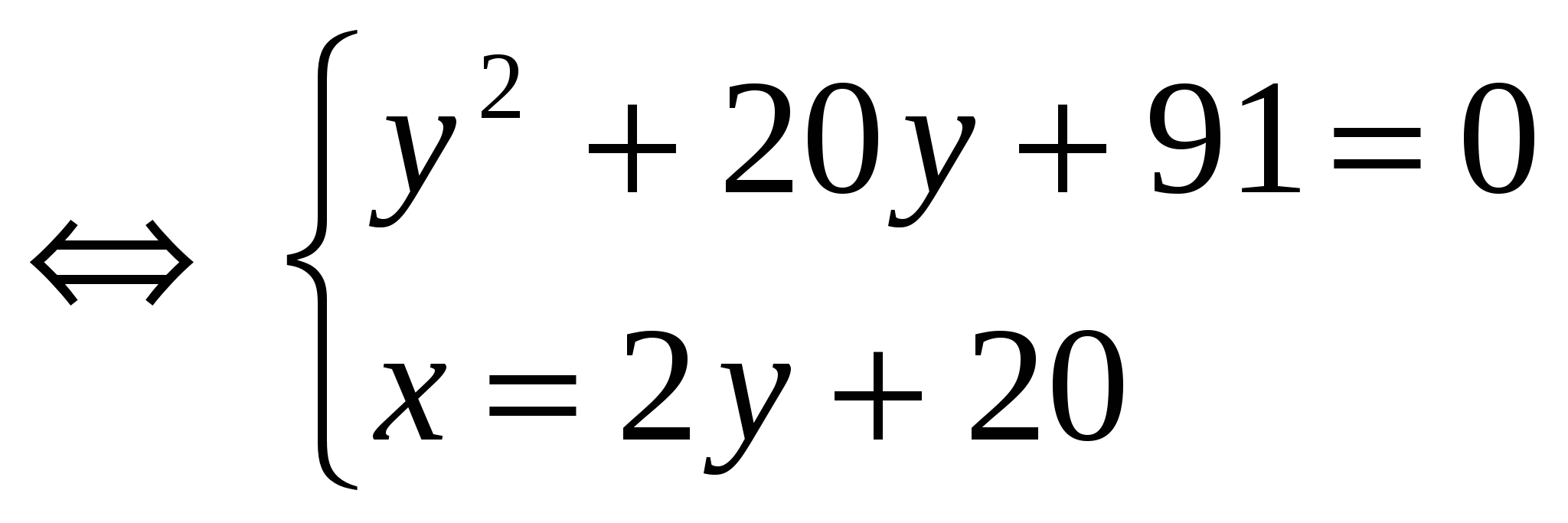
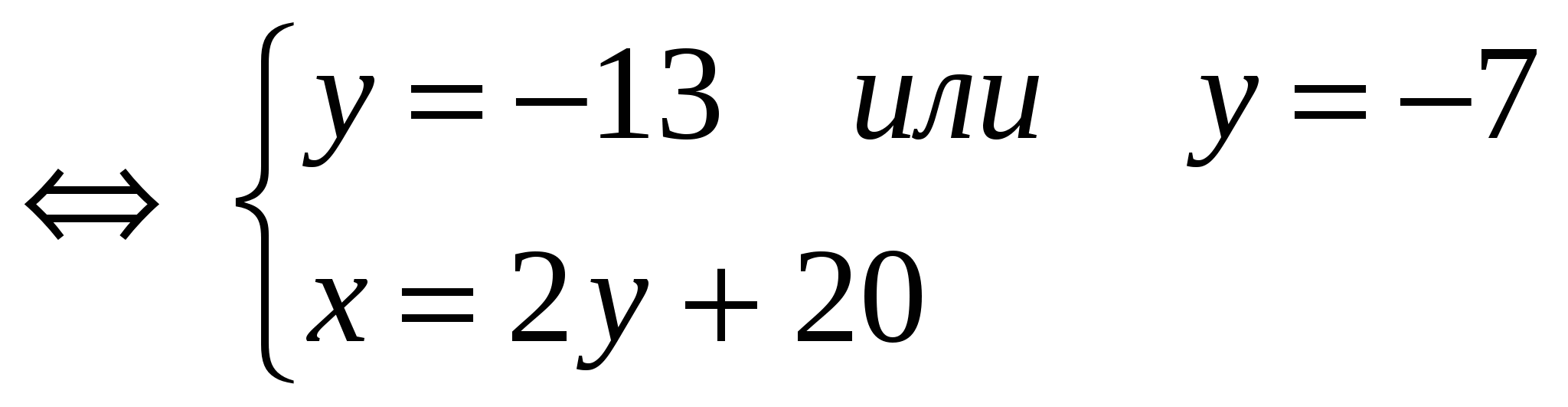
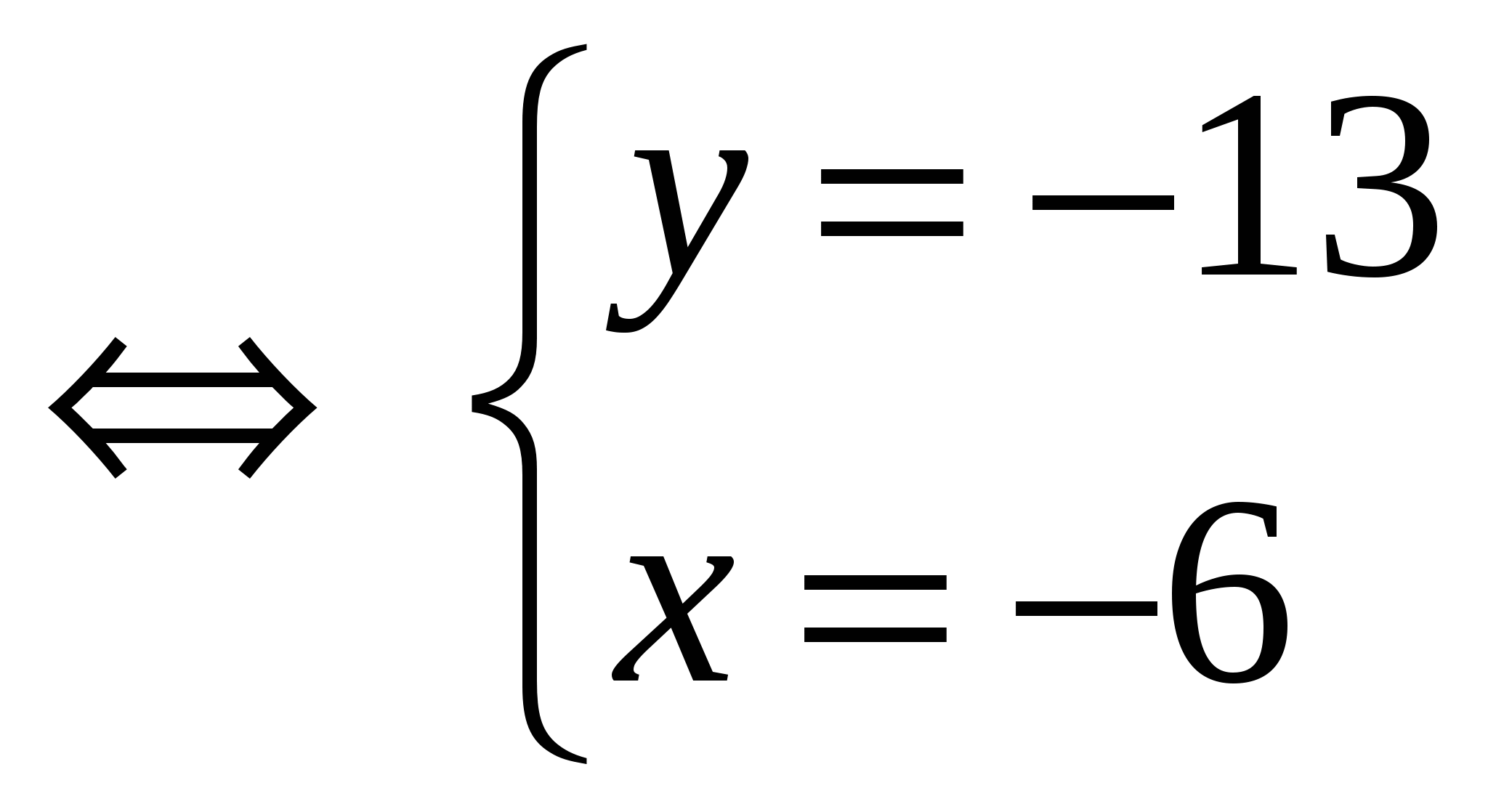 или
или 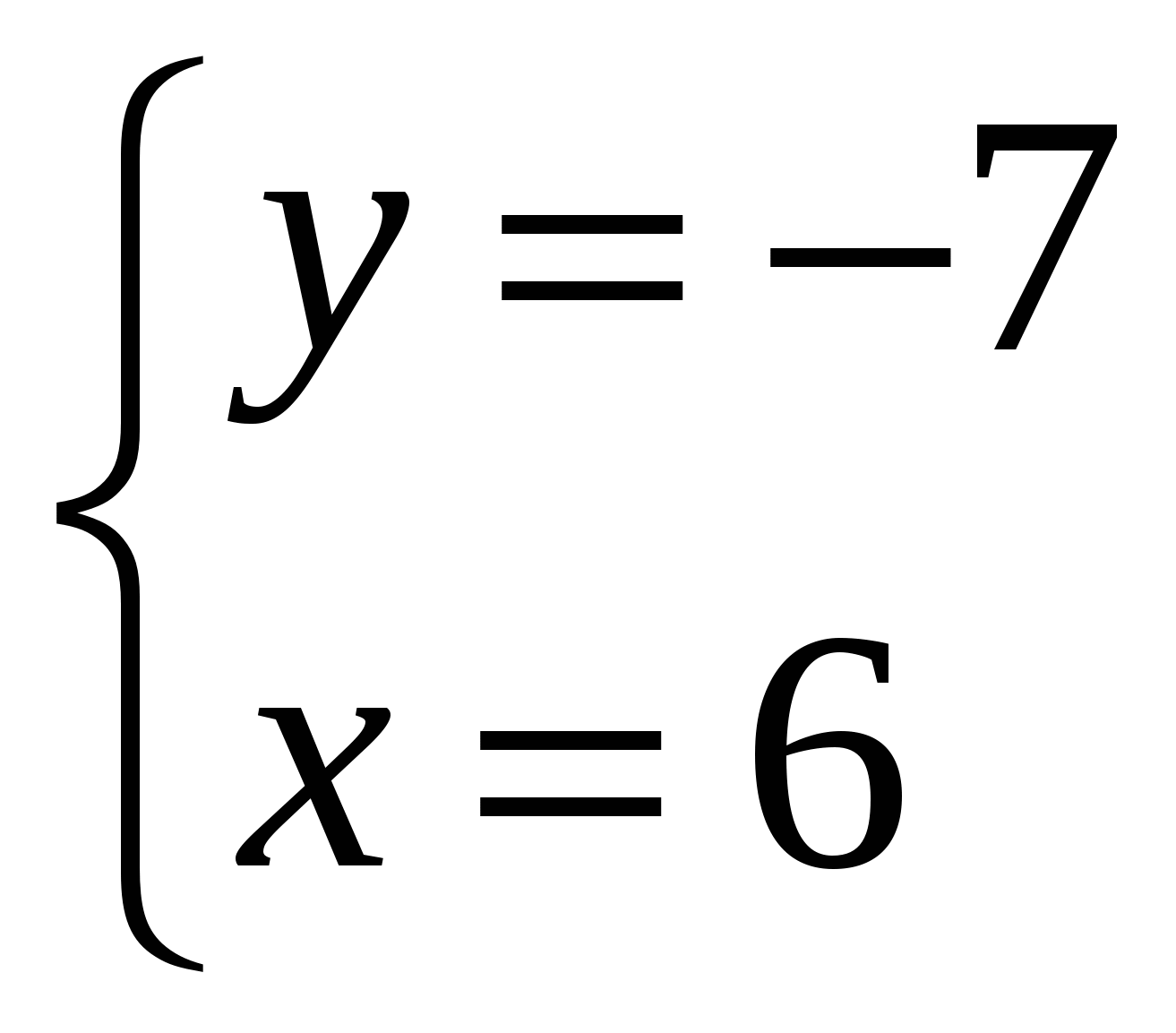


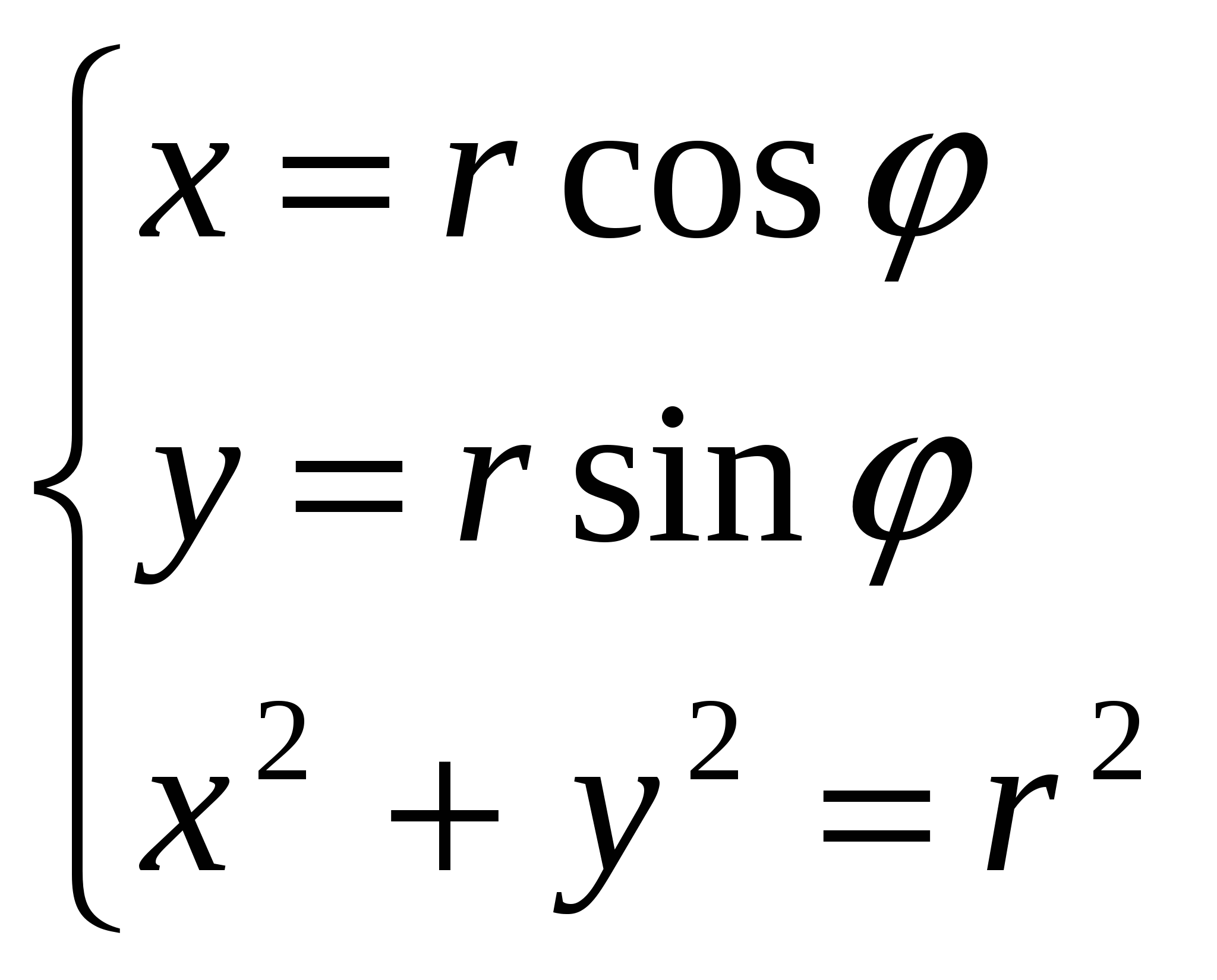 получим
получим