контрольная. Контрольная работа, вариант 9. Контрольная работа 1 Вариант9 Материальная точка движется вдоль прямой ox согласно уравнению
 Скачать 17.71 Kb. Скачать 17.71 Kb.
|
|
Контрольная работа №1 Вариант-9 Материальная точка движется вдоль прямой OX согласно уравнению 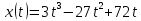 . Проанализируйте характер движения точки. Определите путь . Проанализируйте характер движения точки. Определите путь 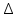 S, модуль перемещения | S, модуль перемещения |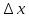 |, среднюю скорость < |, среднюю скорость < 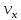 > и среднюю путевую скорость < > и среднюю путевую скорость <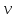 > за указанный интервал времени > за указанный интервал времени 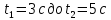 . .Дано: 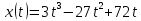 . .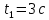 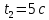 . .Найти: 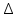 S-?; S-?; 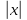 ; ; 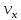 ; ; 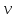 Решение: Исследуем характер движения точки по плану: 1)Найдем начальную координату точки 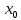 в момент времени в момент времени 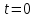 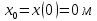 2) Найдем уравнение скорости точки 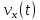 , вычисляя первую производную координаты по времени , вычисляя первую производную координаты по времени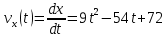 3)Найдем начальную скорость точки 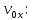 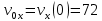 м/с м/сТак как 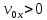 значит, точка начинает движение вдоль положительного направления оси значит, точка начинает движение вдоль положительного направления оси 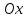 4)Определим моменты остановок(или разворотов) точки 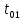 , , 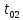 решая уравнение решая уравнение 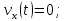 Квадратное уравнение 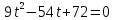 имеет два корня имеет два корня 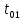 =2 с и =2 с и 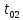 =4 с =4 с5) Определим координаты точки при разворотах 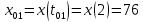 м м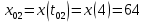 м м6) Найдем уравнение ускорения 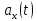 точки первую производную скорости по времени точки первую производную скорости по времени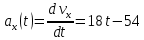 7) Начальное ускорение 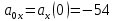 м/ м/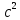 8) Скоростной режим движения с переменным ускорением меняется не только при разворотах точки, но и в момент времени, когда ускорение меняет знак. Найдем момент времени 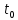 когда когда 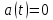 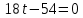 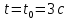 То есть 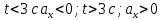 9) Проанализируем характер движения , учитывая все моменты смены скоростного режима. Рассмотрим все характерные моменты времени в порядке возрастания и образуем четыре интервала с постоянным скоростным режимом. Так в интервале времени (0 с; 2с): 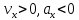 , значит точка движется замедленно вдоль оси Ох; , значит точка движется замедленно вдоль оси Ох;В интервале времени (2 с; 3с): 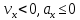 , значит точка движется ускоренно против оси Ох; , значит точка движется ускоренно против оси Ох;В интервале времени (3с; 4с): 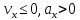 . Точка движется замедленно против оси Ох; . Точка движется замедленно против оси Ох;Начиная с 4 с: 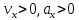 что соответствует ускоренному движению вдоль оси Ох что соответствует ускоренному движению вдоль оси Ох10) Найдем модуль перемещения 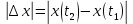 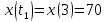 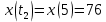 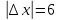 11) Найдем среднюю скорость 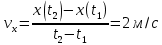 12) Найдем путь складывая путь, пройденный до разворота за интервал времени (3 с; 4 с) и путь , пройденный после разворота за интервал времени (4с; 5с) 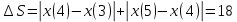 м м13)Найдем среднюю путевую скорость м 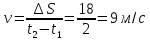 2.Колесо радиусом R=10 см вращается так, что зависимость угла поворота радиуса колеса, угловой скорости и углового ускорения от времени описывается уравнением φ(t), ω(t), ε(t) соответственно. В таблице 2 приведены кинематические характеристики движения колеса в момент времени, принятый за начальный (t=0) и уравнение временной зависимости одной из рассматриваемых величин. Напишите уравнения φ(t), ω(t), ε(t), если A= 0,01π рад/с2 , B= 0,1 рад/с., Определите полное ускорение а точки, находящейся на ободе колеса в момент времени t= 10c. Угол поворота задан в радианах. ЗАДАЧА 3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА Пуля массой m, летящая с горизонтальной скоростью V0 , попадает в шар с массой M, подвешенный на невесомой нерастяжимой нити длиной l и застревает в нем. Доля кинетической энергии пули, перешедшей в тепло при ударе, равна β. Шар сразу после удара приобретает скорость V и поднимается на высоту h, нить при этом отклоняется от вертикали на угол α. Минимальная скорость шара в верхней точке траектории, при которой он может совершить полный оборот вокруг точки подвеса, равна V1. 4. Однородный тонкий стержень длиной l и массой М может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через точку 0 (рис. 4). Расстояние от верхнего конца стержня до точки 0 равно r1. Пуля массой m, летящая в горизонтальном направлении со скоростью υ0, попадает в точку А стержня и застревает в нем. Расстояние от верхнего конца стержня до точки А равно r2. Линейная скорость нижнего конца стержня непосредственно после удара равна υ, а угловая скорость его равна ω. Угол отклонения стержня после удара равен φ. Момент инерции стержня относительно оси вращения равен J. Данные для всех вариантов приведены в табл. 4 |
