Аналитическая геометрия. Контрольная работа 1. Контрольная работа 1. Вариант Т. 1. По координатам вершин пирамиды а 1 а 2 а 3 а 4 найти

• Название: Контрольная работа 1. Вариант Т. 1. По координатам вершин пирамиды а 1 а 2 а 3 а 4 найти
• Анкор: Аналитическая геометрия
• Дата: 15.02.2023
• Размер: 233.5 Kb.
• Имя файла: Контрольная работа 1.doc
• Тип: Контрольная работа; #937863

Контрольная работа №1.

Вариант Т.

№1. По координатам вершин пирамиды А₁А₂А₃А₄ найти:

1) длины ребер А₁А₂ и А₁А₃;

2) угол между ребрами А₁А₂ и А₁А₃;

3) площадь грани А₁А₂А₃;

4) объем пирамиды;

5) уравнения прямой А₁А₂;

6) уравнение плоскости А₁А₂А₃;
7) угол между ребром А₁А₄ и гранью А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

Координаты пирамиды:

А₁ (-1; 2; 1)

А₂ (-2; 2; 5)

А₃ (-3; 3; 1)

А₄ (-1; 4; 3)

Решение:

Выполняем дополнительные расчеты.

Координаты векторов находим по формулам:

X = x_j – x_i; Y = y_j – y_i; Z = z_j – z_i

(где X,Y,Z координаты вектора; x_i, y_i, z_i – координаты точки А_i; x_j, y_j, z_j – координаты точки А_j)

A₁A₂ = (– 2 – (– 1); 2 – 2; 5 – 1) = (– 1; 0; 4)

A₁A₃ = (– 3 – (– 1); 3 – 2; 1 – 1) = (– 2; 1; 0)

A₁A₄ = (– 1 – (– 1); 4 – 2; 3 – 1) = (0; 2; 2)

A₂A₃ = (– 3 – (– 2); 3 – 2; 1 – 5) = (– 1; 1; – 4)

A₂A₄ = (– 1 – (– 2); 4 – 2; 3 – 5) = (1; 2; – 2)

A₃A₄ = (– 1 – (– 3); 4 – 3; 3 – 1) = (2; 1; 2)

1) длины ребер А₁А₂ и А₁А₃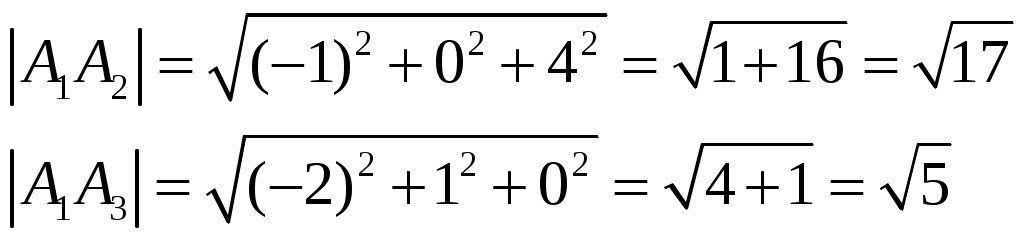

– формула длины вектора



2) угол между ребрами А₁А₂ и А₁А₃

Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: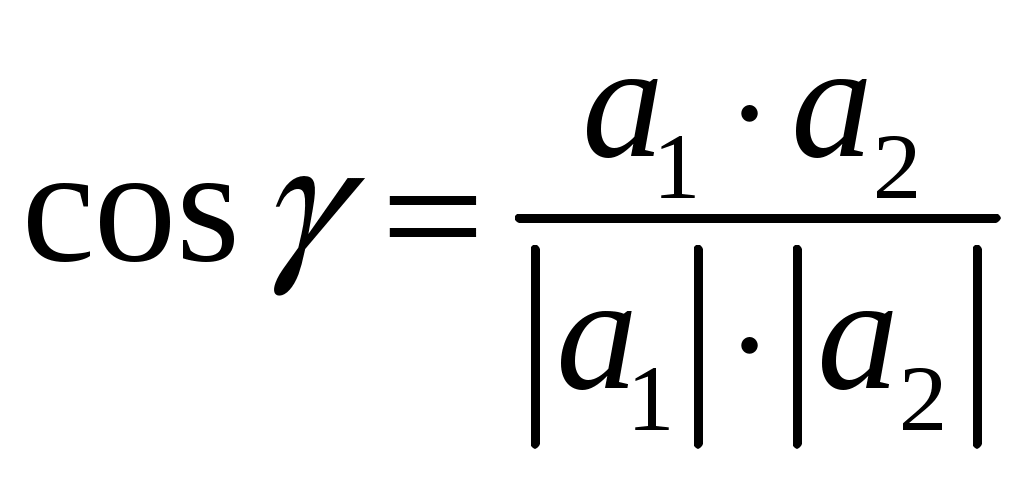

a₁· a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂

Найдем угол между ребрами A₁A₂(– 1; 0; 4) и A₁A₃(– 2; 1; 0):



3) площадь грани А₁А₂А₃

Площадь грани можно найти по формуле:

, где .

Найдем площадь грани A₁A₂A₃.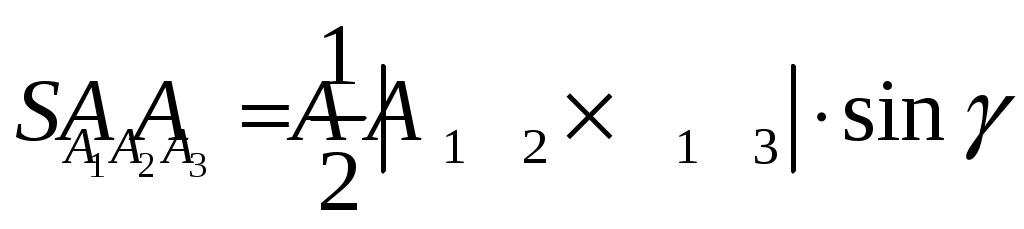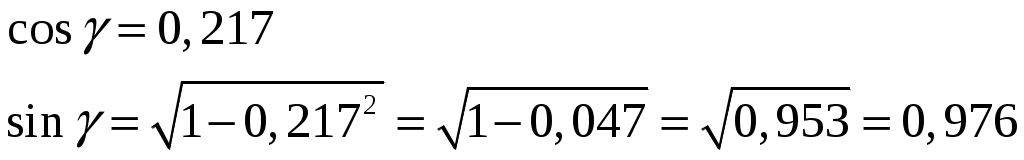



Площадь грани находим с учётом геометрического смысла векторного произведения. Векторное произведение: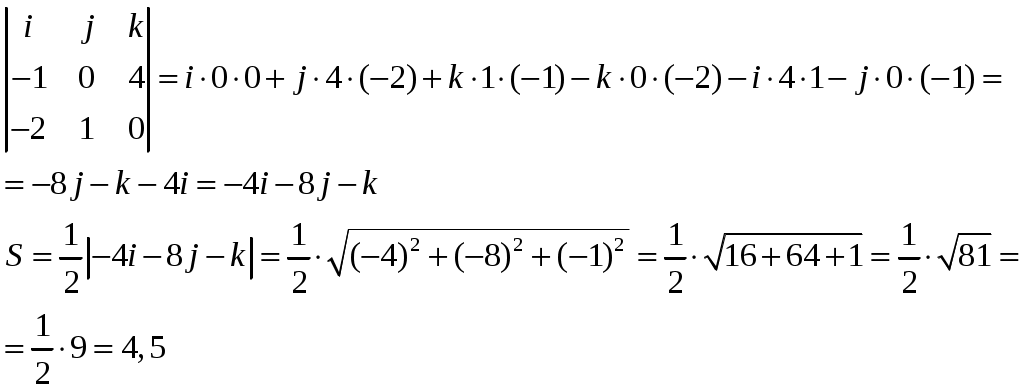



4) объем пирамиды

Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: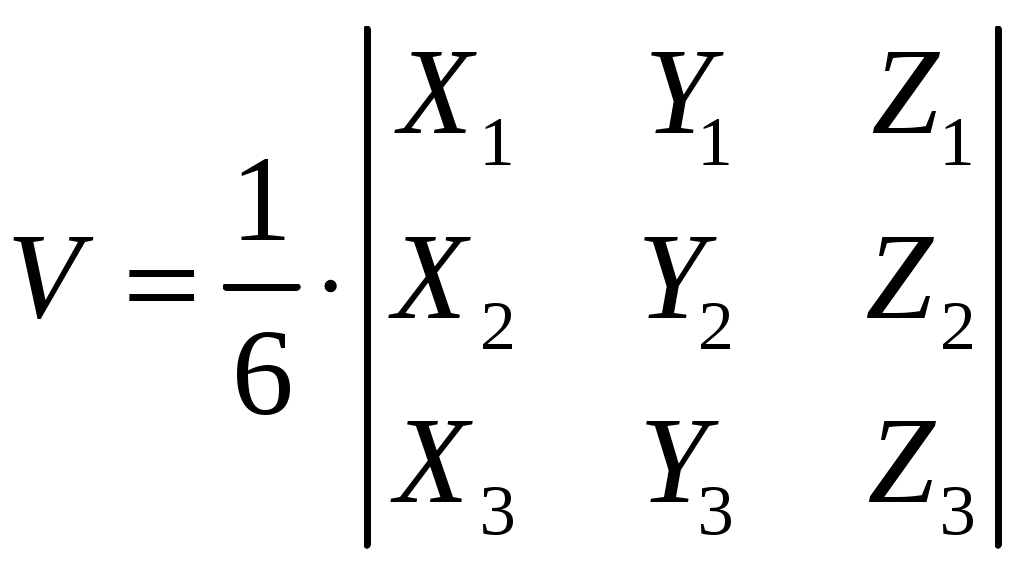



Определитель вычисляем по правилу треугольника.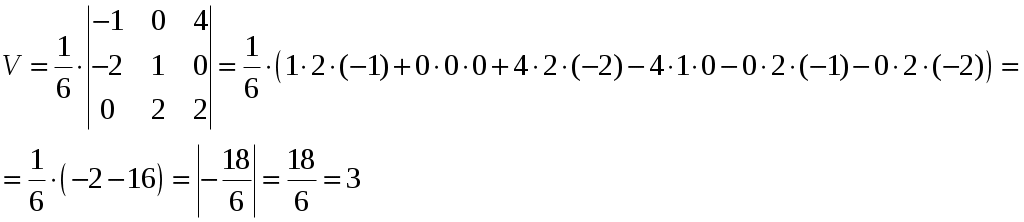

5) уравнения прямых А₁А₂ и А₁А₃

Прямая, проходящая через точки A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂), представляется уравнениями: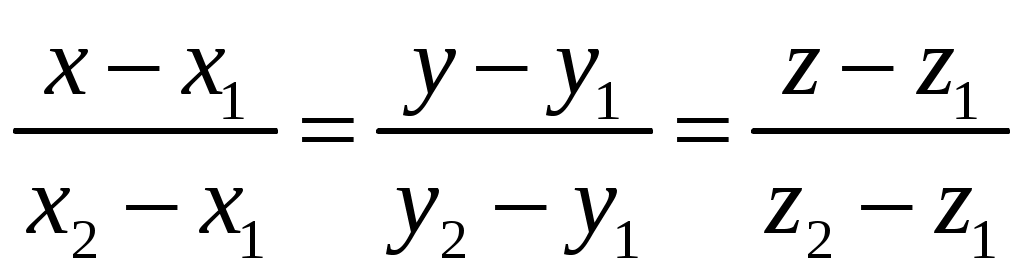

Уравнение прямой A₁A₂: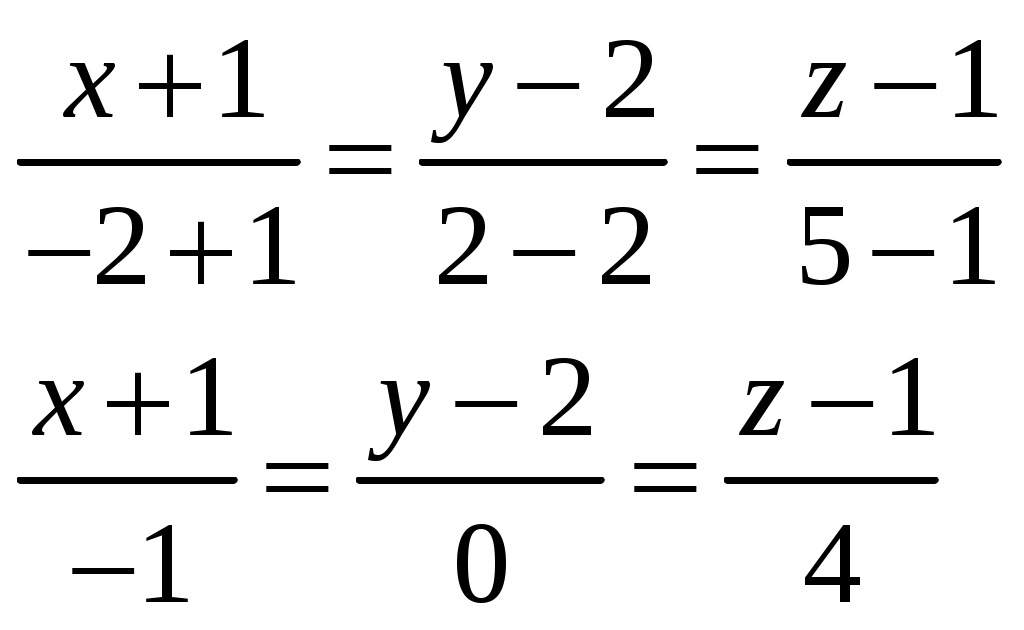

Уравнение прямой A₁A₃: .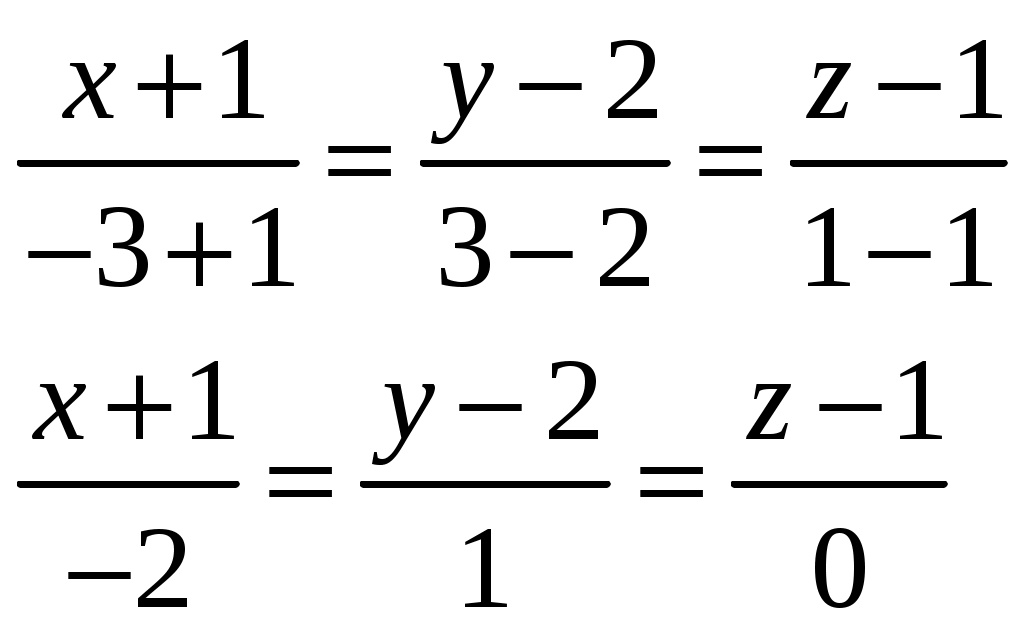

6) уравнение плоскостей А₁А₂А₃ и А₁А₂А₄

Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: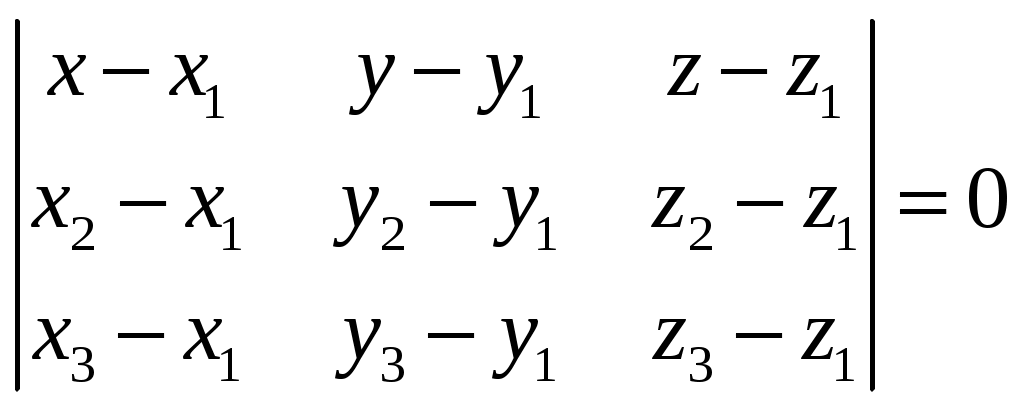



Уравнение плоскости A₁A₂A₃: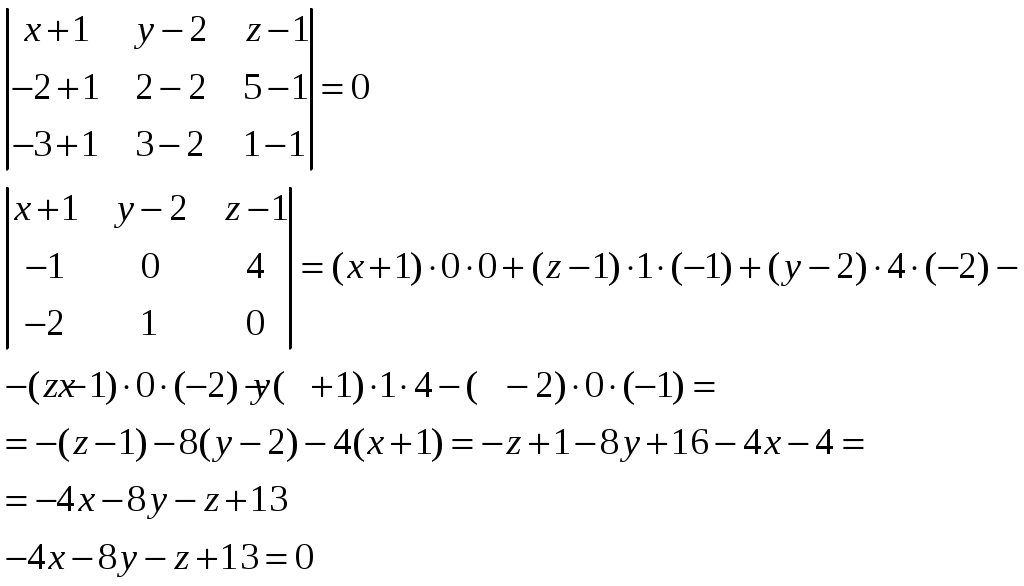


Уравнение плоскости A₁A₂A₄: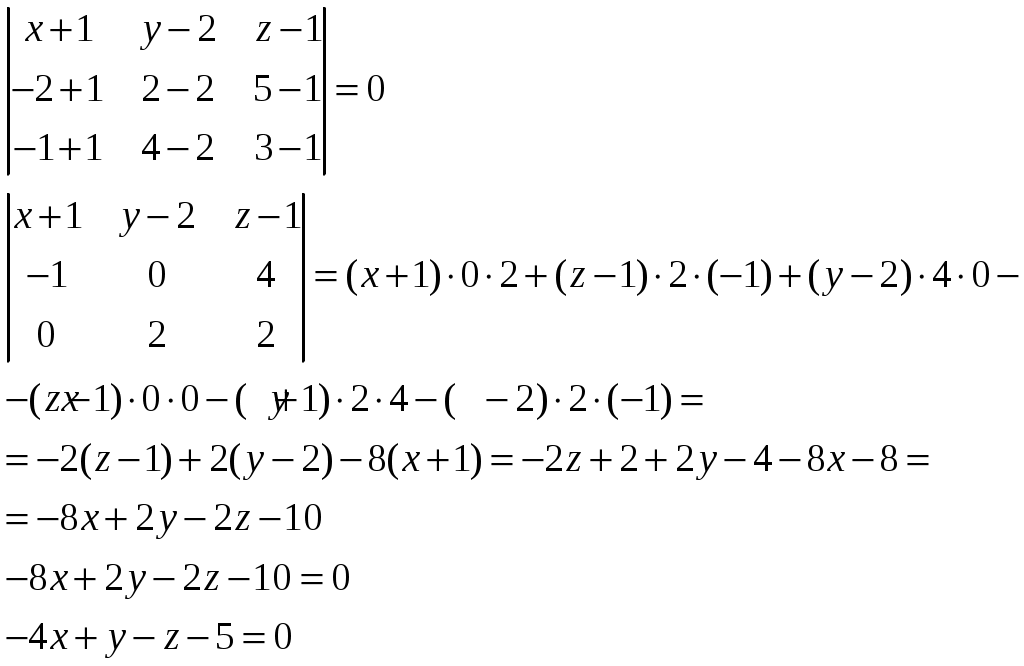



7) угол между плоскостями А₁А₂А₃ и А₁А₂А₄.

Косинус угла между плоскостью А₁x + B₁y + C₁ + D = 0 и плоскостью А₂x + B₂y + C₂ + D = 0 равен углу между их нормальными векторами N₁(А₁; B₁; C₁) и N₂(А₂; B₂; C₂).

Уравнение плоскости А₁А₂А₃:

N₁(– 4; – 8; – 1)

Уравнение плоскости А₁А₂А₄:

N₂(– 4; 1; – 1)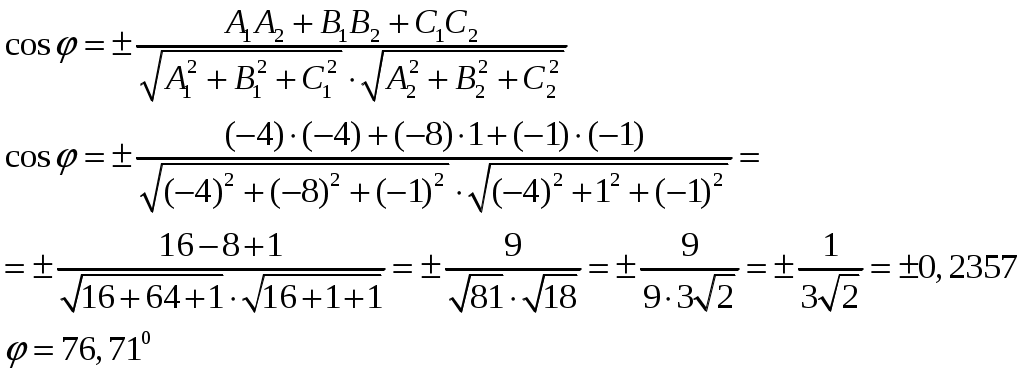



№2. Требуется:

1) построить по точкам график функции 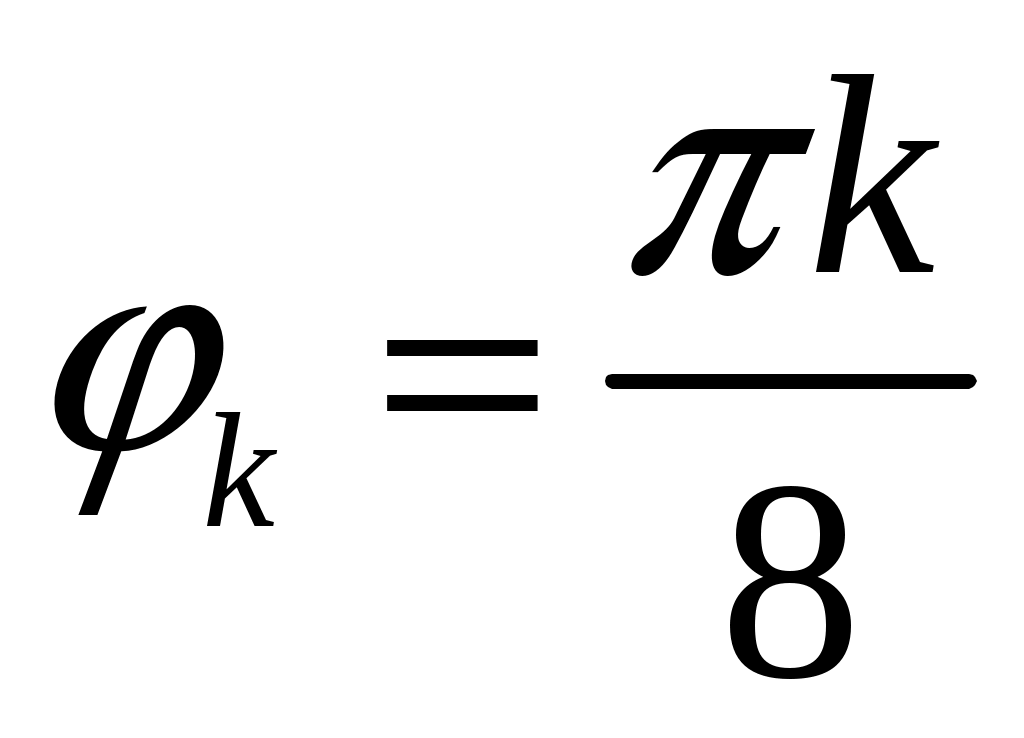в полярной системе координат. Значения функции вычислять в точках ;

2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ох – с полярной осью;

3) определить вид кривой.

Решение:

1) Находим область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство .

Область определения нашей функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).

Находим точки принадлежащие графику функции – составляем таблицу значений.

	0
	6	5,5434	4,2426	2,2962	0

В силу чётности косинуса соответствующие положительные значения можно заново не считать:

	0	–	–	–	–
	6	5,5434	4,2426	2,2962	0

Изобразим полярную систему координат и отложим найденные точки на прямых с углом поворота . Соединяем полученные точки. Получаем окружность.




2) Найдём уравнение кривой в декартовой (прямоугольной) системе координат.

Обе части уравнения домножаем на :

и используем более компактные формулы перехода

Получаем:

Выделяя полный квадрат, приводим уравнение линии к узнаваемому виду: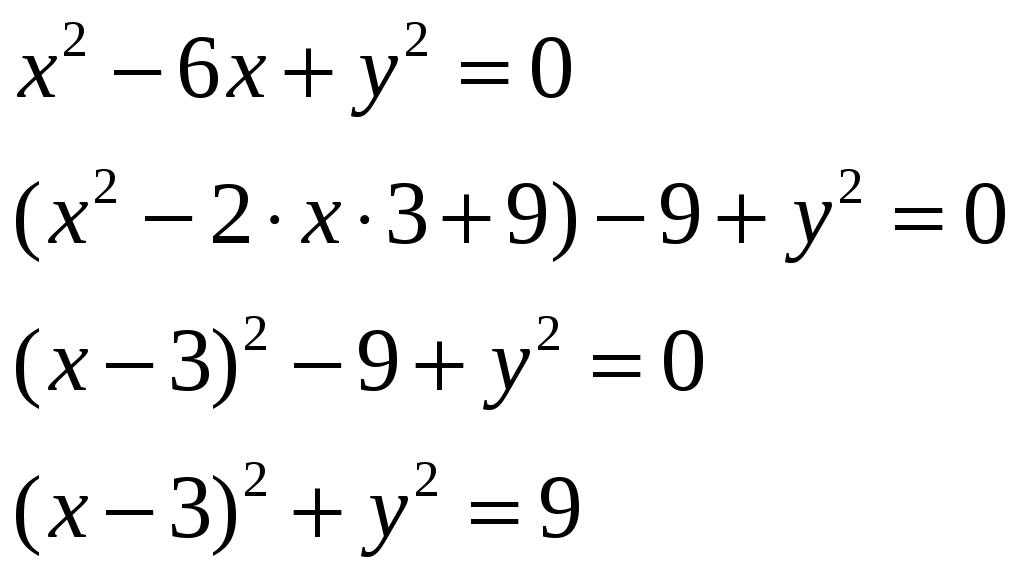



3) Получили уравнение окружности с центром в точке (3; 0), радиуса 3.

№2. Дана система трех линейных уравнений с тремя неизвестными. Требуется:

1. 
   найти ее решение с помощью формул Кремера;
   
2. 
   записать систему в матричной форме и решить ее средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.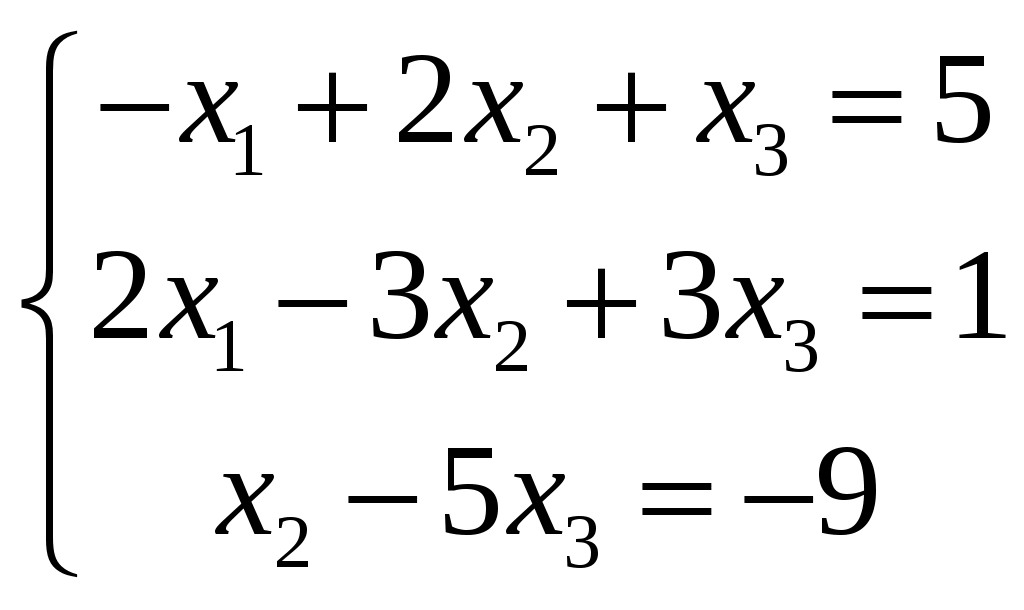
   

.
Решение: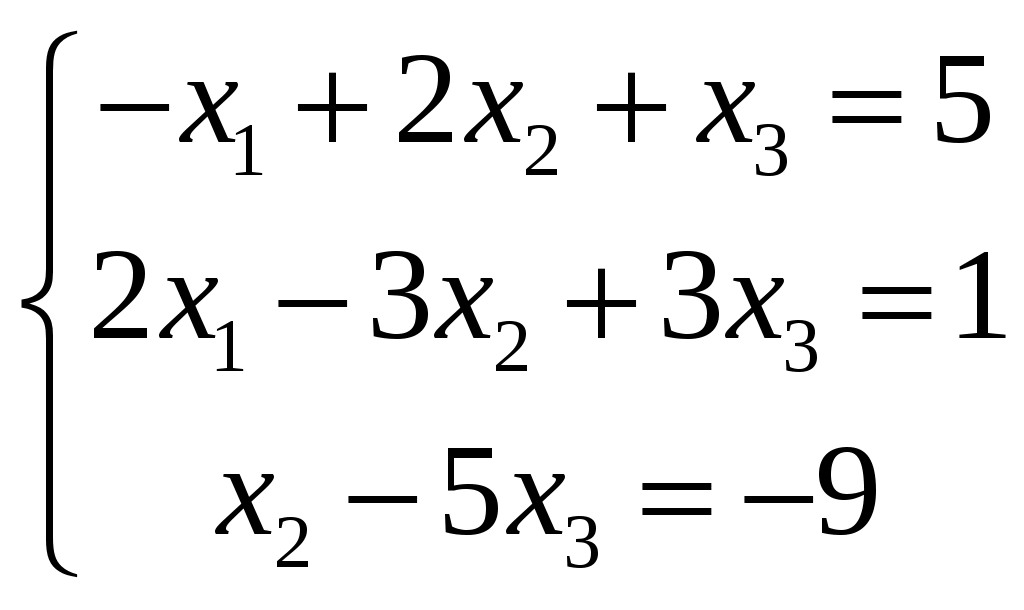



1) Вычисляем главный определитель по правилу треугольника: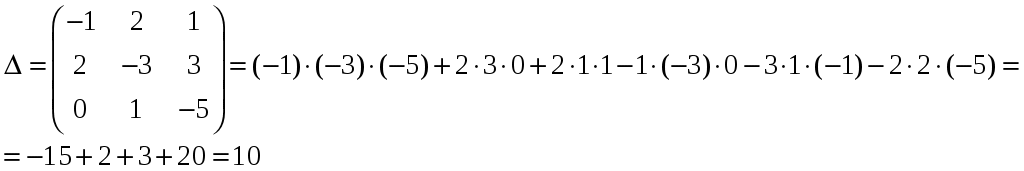



Записываем и вычисляем первый определитель, для вычисления х₁: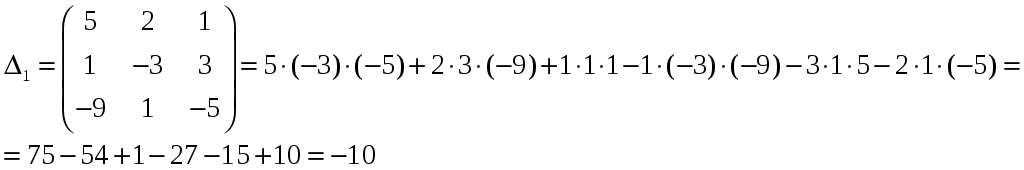

Записываем и вычисляем первый определитель, для вычисления х₂: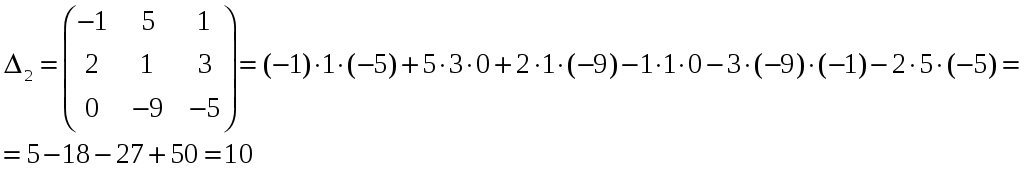

Записываем и вычисляем первый определитель, для вычисления х₃: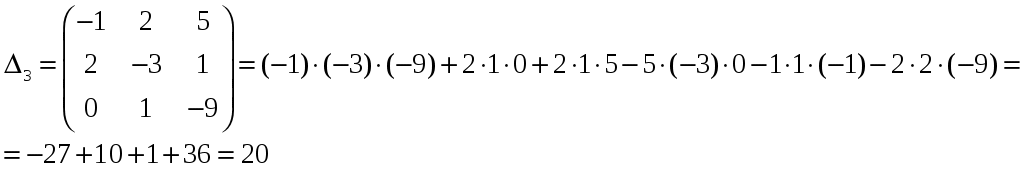

Найдем решения данной системы по формулам: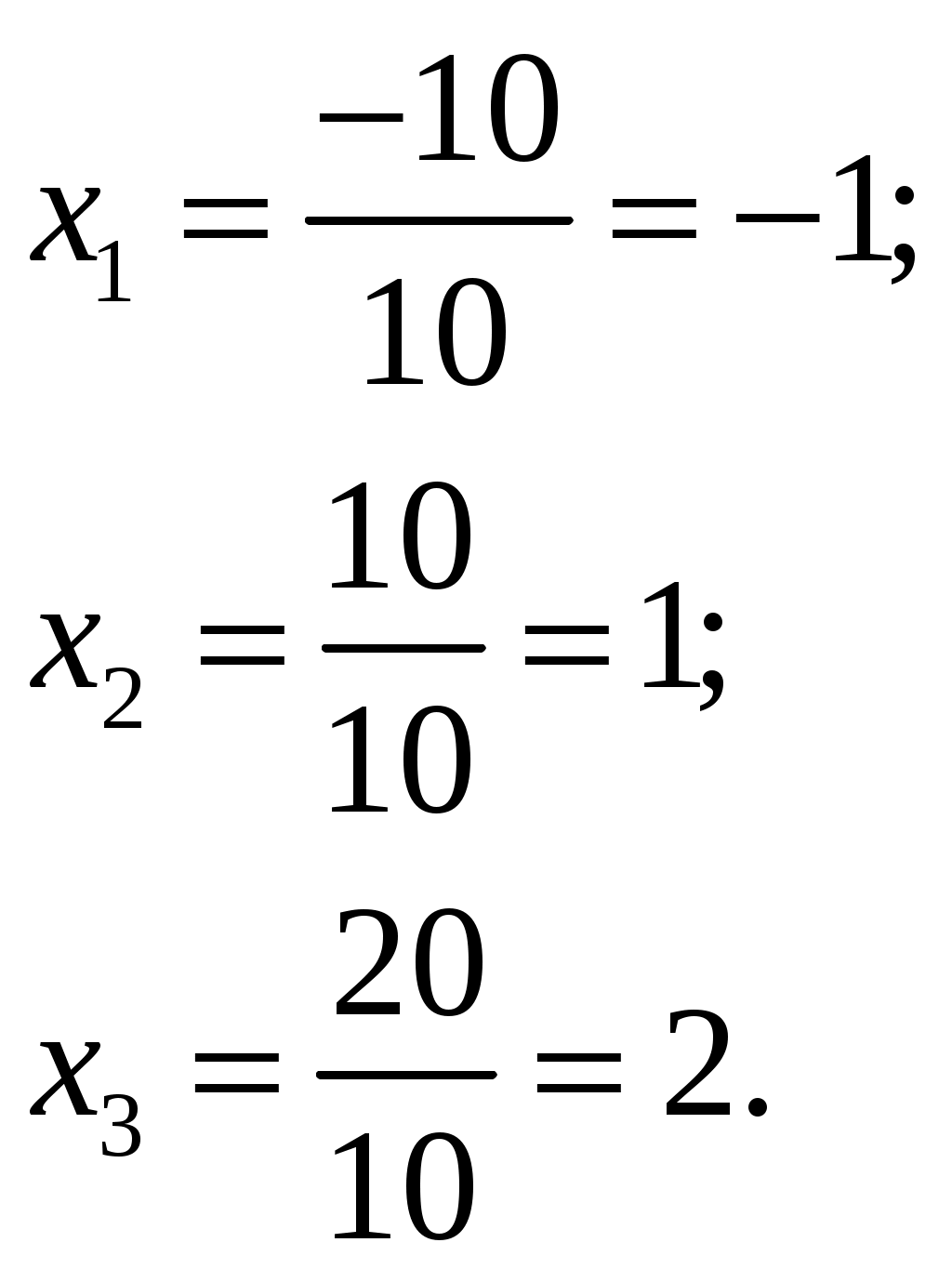



2) Запишем систему уравнений в матричной форме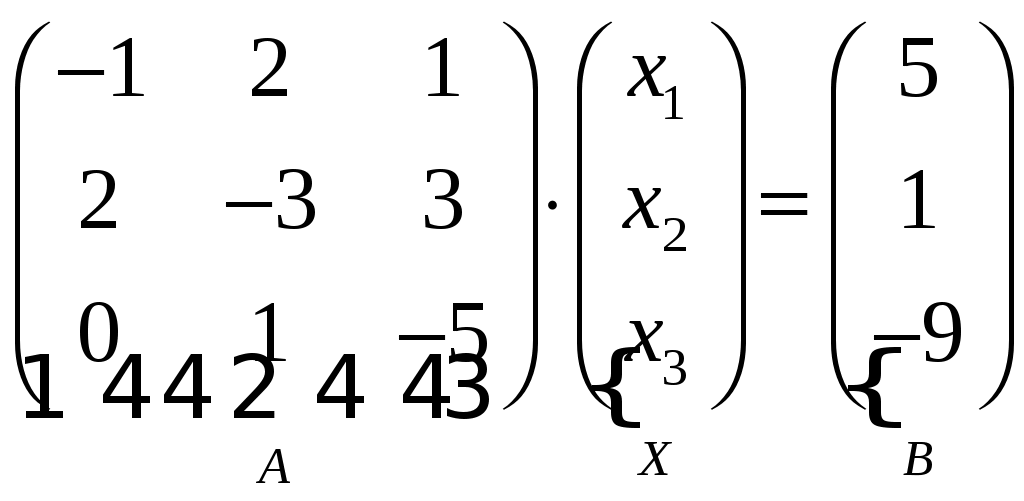

А· Х = В

Х = А^-1 · В

Определитель матрицы А уже найден и |A| = 10.

Для нахождения обратной матрицы вычислим алгебраические дополнения для элементов матрицы А.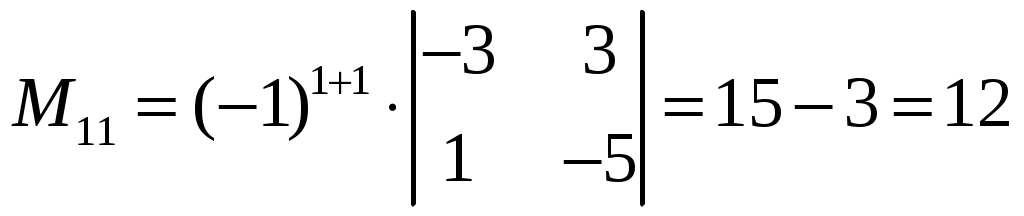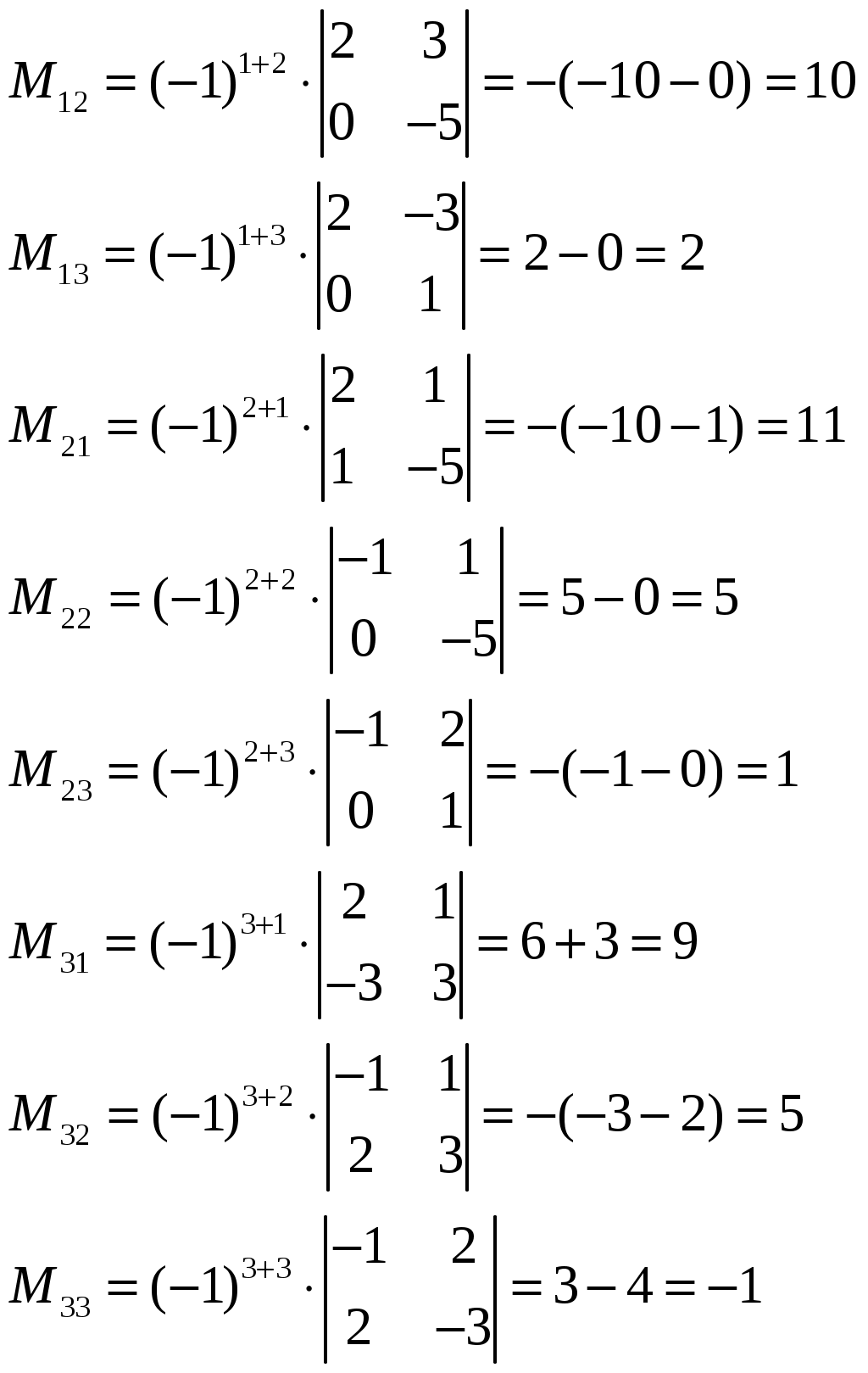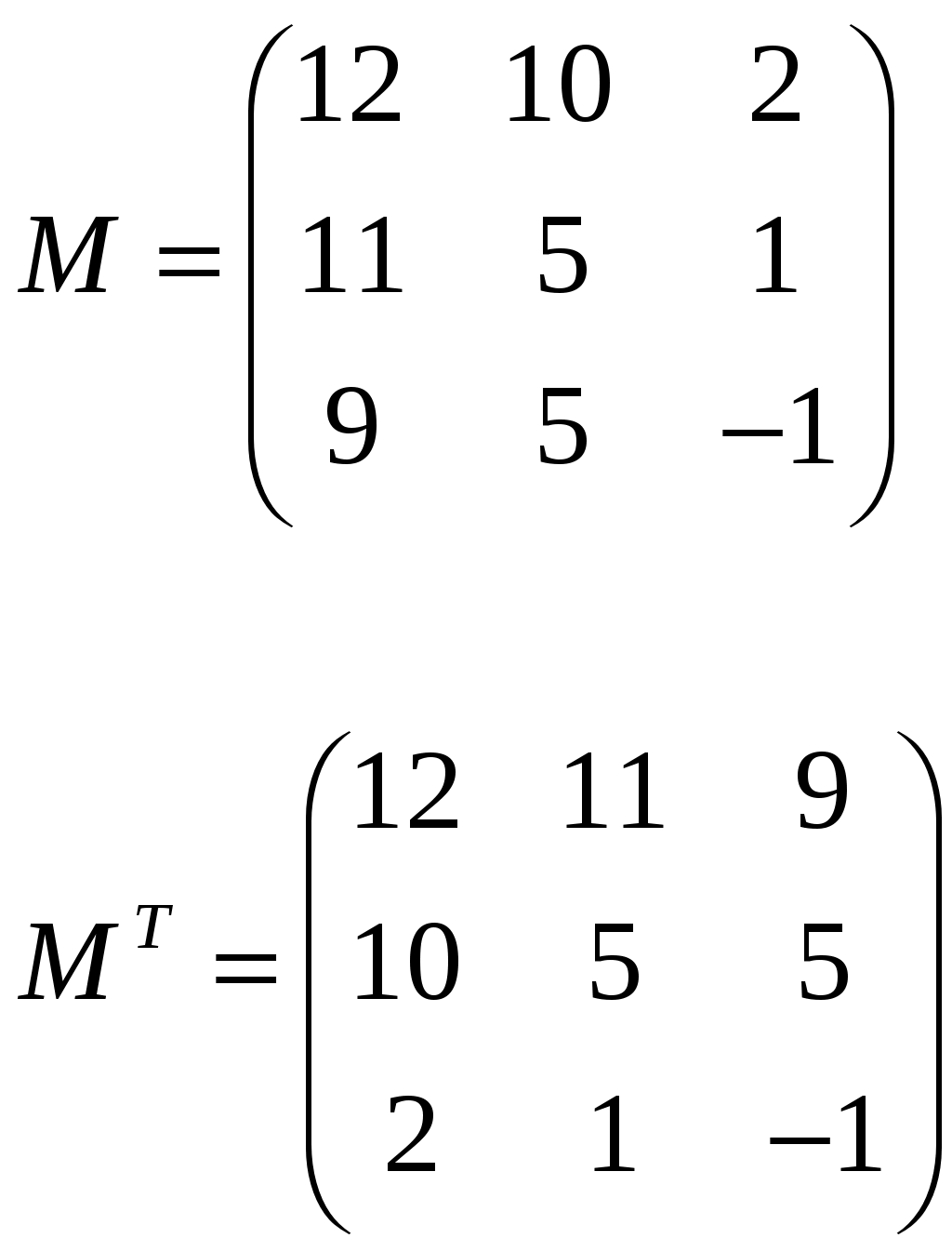







Найдем обратную матрицу: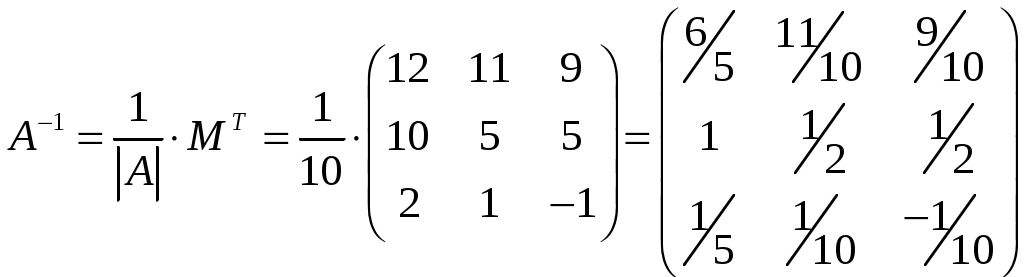



Проверим правильность вычисления обратной матрицы, используя матричное умножение.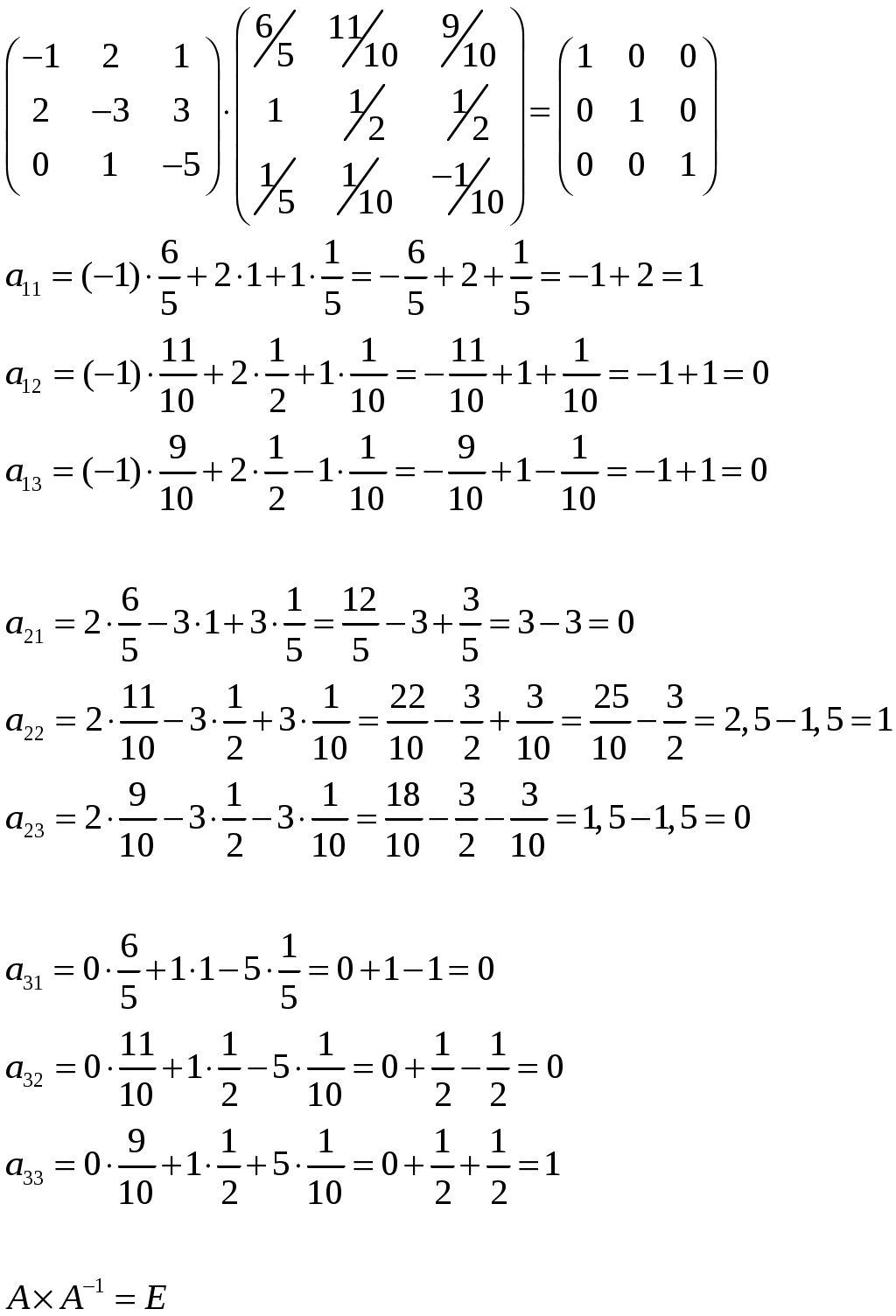



Возвращаемся к решению матричного уравнения.



Ответ: х₁ = – 1; х₂ = 1; х₃ = 2.
№3. Найти множество решений однородной системы трех линейных уравнений с четырьмя неизвестными .

Решение:

Составляем расширенную матрицу системы и приводим ее к ступенчатому виду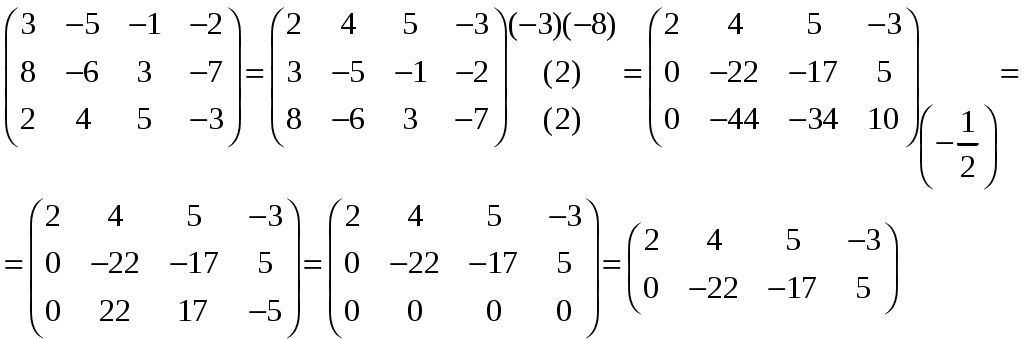



Переменные х₁ и х₂ – базисные, х₃ и х₄ – свободные.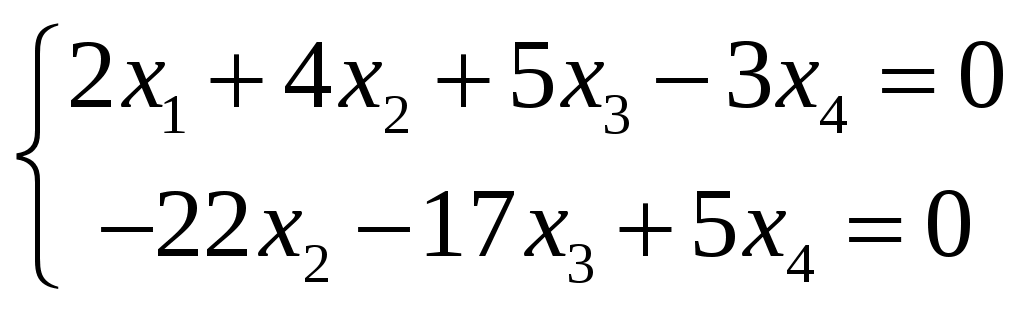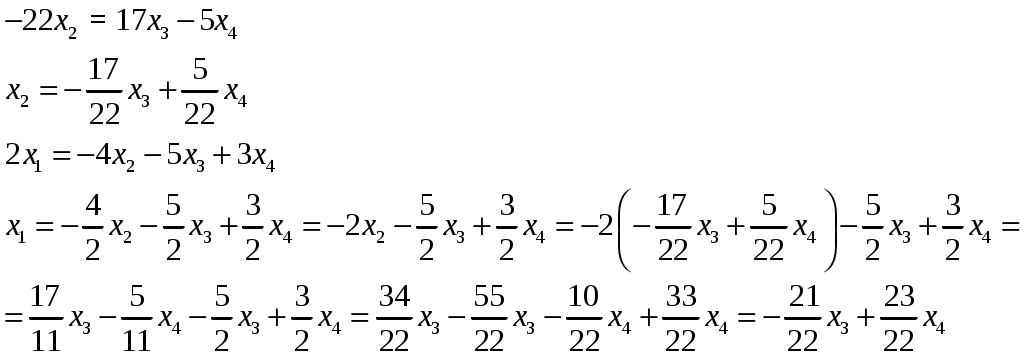





Общее решение однородной системы имеет вид:



Фундаментальное решение системы так как n = 4, r = rgA = 2, то надо подобрать n – r = 2 линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных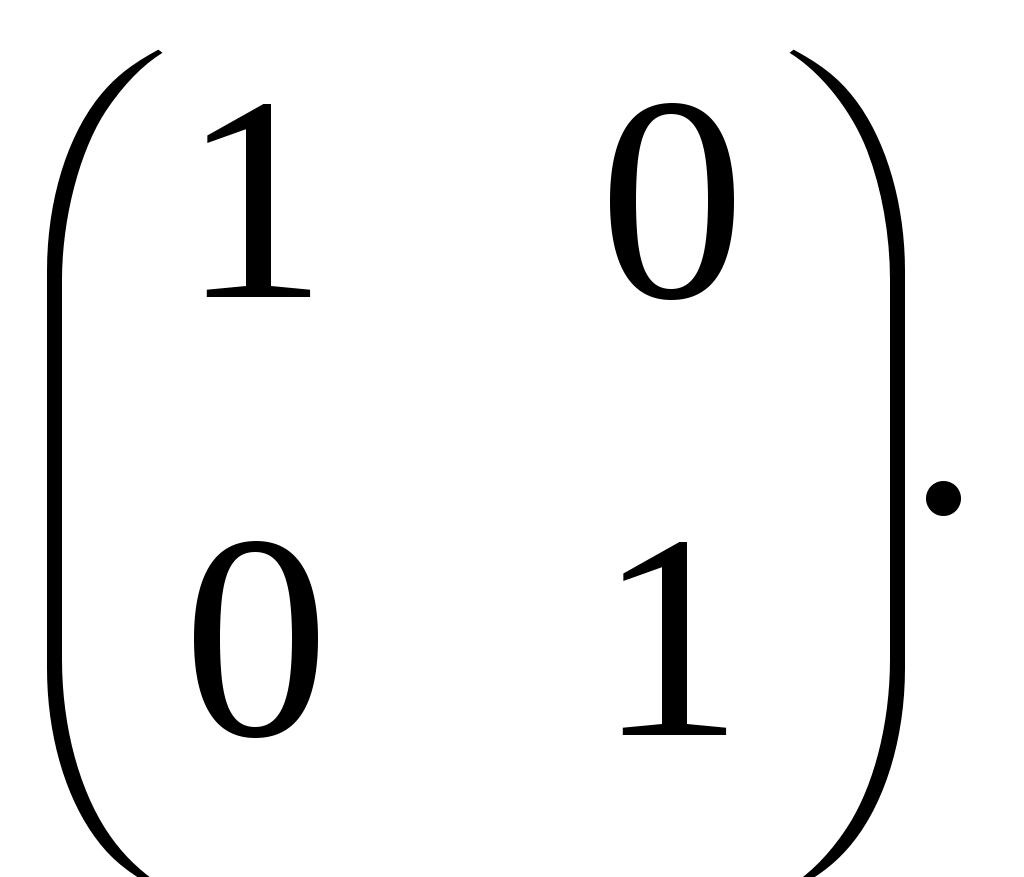

1. 
   Если х₃ = 1, то х₄ = 0, то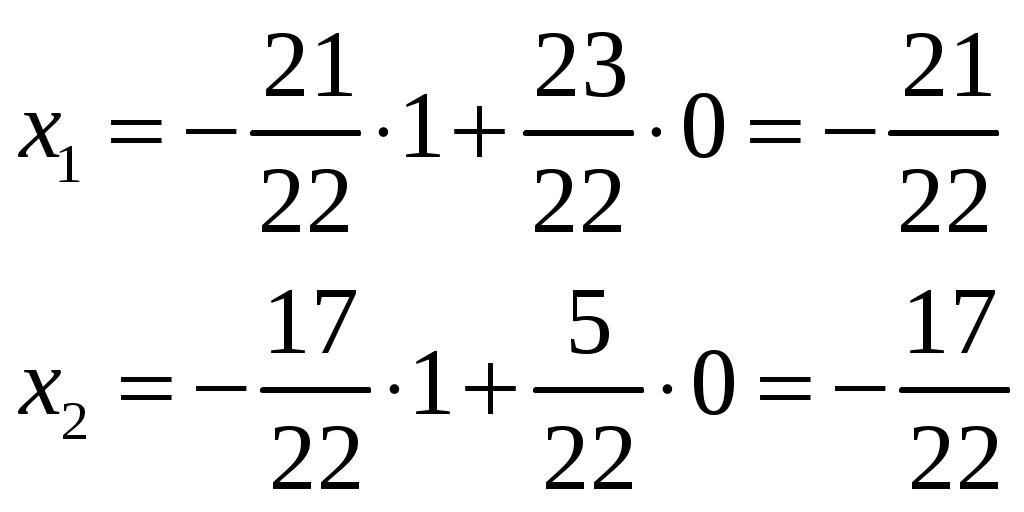
   

2. 
   Если х₃ = 0, то х₄ = 1, то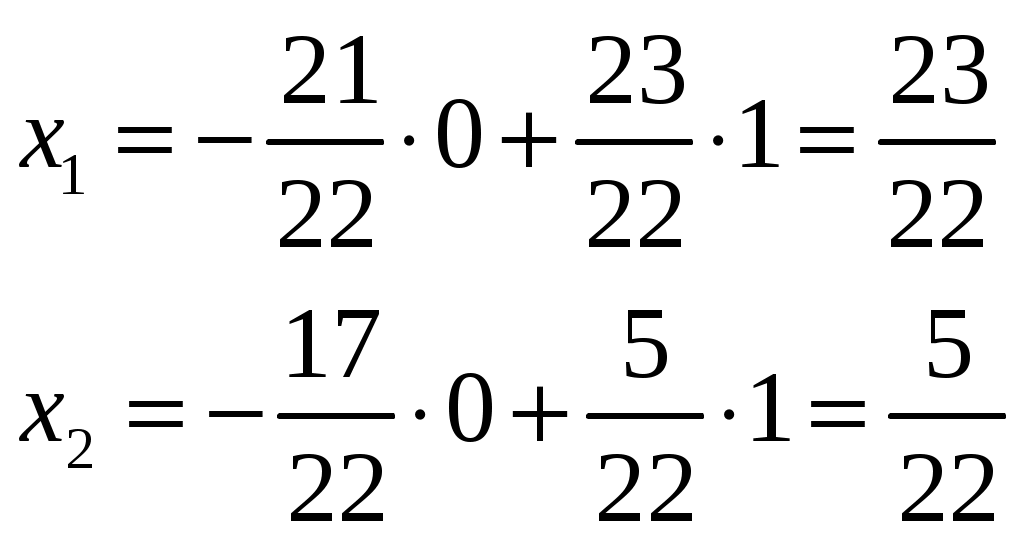
   

В результате получили фундаментальную систему решений: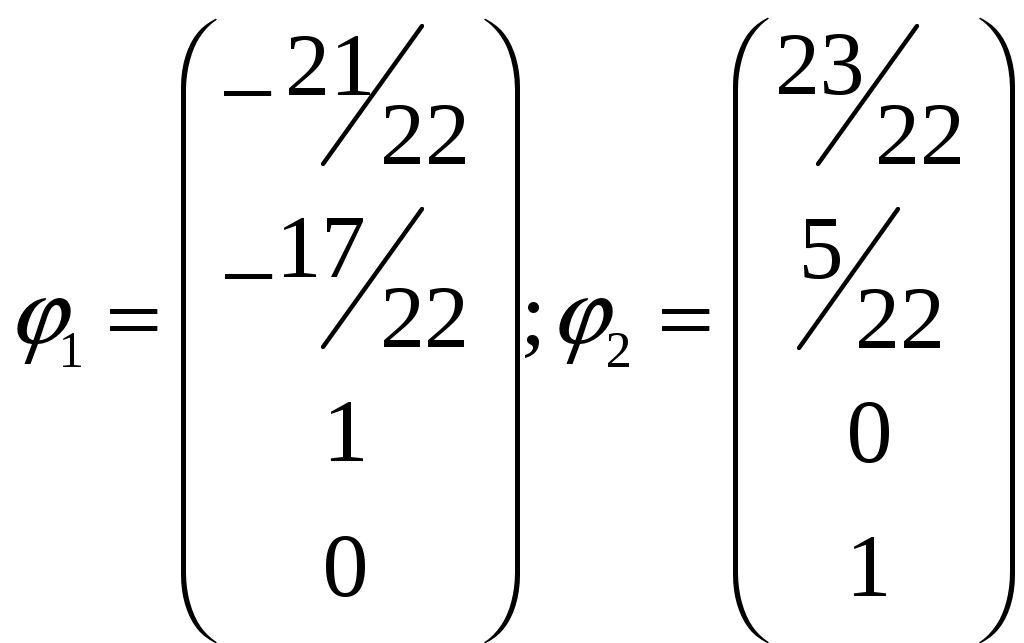



Общее решение однородной системы: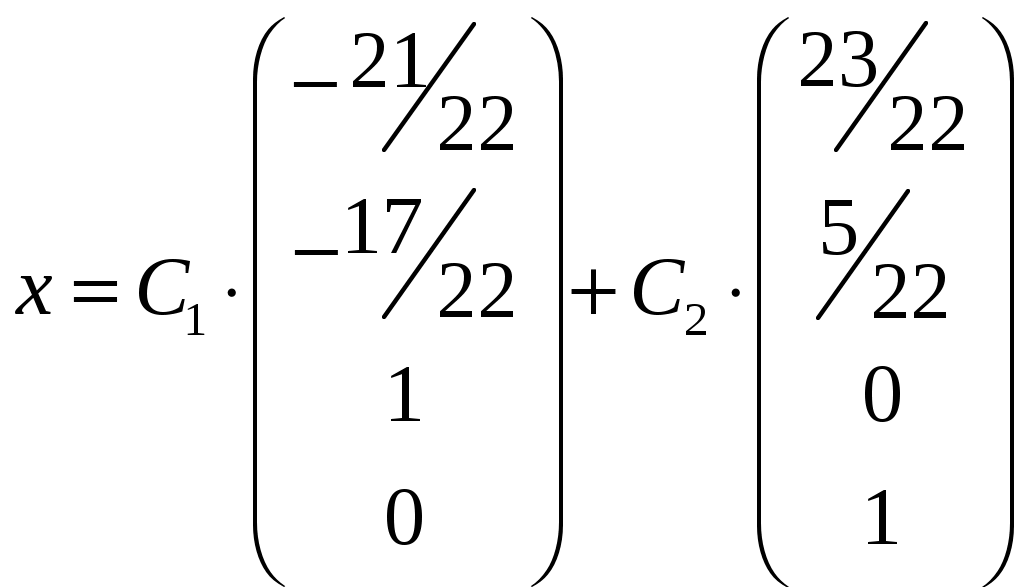