информатика. Контрольная работа 1 задача 1( 15) Числа и переменные Записать данные числа на языке Бейсик Решение задачи
 Скачать 257.43 Kb.
|
|
Контрольная работа № 1 задача №1( № 15) Числа и переменные Записать данные числа на языке Бейсик Решение задачи: Перевод из числа в естественную форму, и в экспоненциальную форму записи 100,5 = 100.5 = 1.005 × 100 = 1.005 × 102 = 1.005e2 10-8 = 0.00000001 = 1 × 0.00000001 = 1 × 10-8 = 1e-8 2719 × 10-3 = 2.719 = 2719 × 0.001 = 2719 e-3 -12000 = - 1.2 ×10000 = -1.2 × 104 = - 1.2e + 4 2) Запись готовых данных в таблицу
Б) Указать какие из чисел не соответствуют правилам записи на Бейсике и почему. 1) 0.54E4 2) E2 3) 10E-3 4) 60.2 0.54E4 – не соответствует, так как ненормированное ( от 1 до 10) Е2 – не соответствует, так как нет мантиссы 10E-3 – соответствует 60.2 – как число по правилу Бейсик, не принимается, принимается как массив В) Определить какие из приведённых имён переменных являются неправильными и почему. Н4 TA 7K E2 H4 – правильно, начинается с латинской буквы, заканчивается цифрой, как положено в переменной. TA – правильно, если T и A – латинские буквы 7K – неправильно, так как начинается с цифры E2 – правильно, если E – латинская буква Задача № 2 ( № 35)  2.Описать данную матрицу как двумерный массив. Представить в виде переменных с индексами отрицательные элементы массива. S = -7 -3 4 5 6 -1 Дана матрица S размерностью 2 на 3. DIM S ( 2,3) S(1,1) = -7 S(1,2) = -3 S( 2,3) = -1 Задача № 3( №55) 3. Вычислить значения стандартных функций, записанных на языке бейсик 1) SQR( 121) 2)ABS( -7.1) 3) SGN(37) 4) INT(2.14) SQR(121) – корень квадратный. Корень квадратный из 121 = 11 ABS(-7.1) – модуль числа от -7.1. Получится со знаком « +» = 7.1 модуль числа. SGN(37) Любое положительное число в круглых скобках даёт нам единицу.SGN(37) = 1 INT(2.14) Функция действует таким образом, что отбрасывает дробную часть и выдаёт в результате целую часть числа. Результатом является 2 – наша целая часть числа. Задача № 4 (№75) А) Записать математическое выражение в символах языка Бейсик. 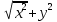 - sin( x+y)Y=2(sqr(X^2 + Y^2) – sin(X+Y) X и Y – заглавные буквы. Б) Представить математическую запись выражения, записанного на языке Бейсик: ABS(( 1-A))/ В) – SQR(LOG( 4+ A/B)) Ответ: 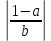 -  )Задача № 5 ( №95) 5.Записать последовательность операторов присваивания величины по заданной формуле. A15=  +  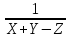Решение. CLS INPUT “x=”,x INPUT “y=”y INPUT “z=”,z A1 = x+y-z A3= sin((1-A1^2)/A1) ELSELF A1 => -1 AND A2 <0 THEN A2= 3.14 + sin((1 – A1^2)/A1) ELSE PRINT. “ Недопустимый аргумент arсcos” : END END IF A15= cos(1/2)(A1))/1 + cos(A2)+(1/(A1) PRINT “A15=”;A19 END Задача № 6 (№115) Присвоить переменным перечисленные ниже значения( в соответствии с вариантом) С1=0.001, С2=0.01, L1=1, L2=16.5, R1=6.8, R2=3.6 С помощью оператора печати соответствующих знаков препинания сформировать на экране текст, сохранив заданное расположение символов. └┴┘Емкость C1=└┘.001└┘C2=└┘.01 └┴┘Индуктивность L1=└┘1└┴┴┴┴┘L2=└┘16.5 └┴┘Сопротивление R1=└┘6.8└┴┴┘R2=└┘3.6 Решение. CLS C1 = 0.001 C2 = 0.01 L1 = 1 L2 = 16.5 R1 = 6.8 R2 = 3.6 PRINT “ Ёмкость └┴┘Индуктивность └┴┘Сопротивление” PRINT “└┘C1=”; С1;” L1=└┘”; L1; ”R1=└┘”; R1 PRINT “└┘C2=”;С2; └┴┴┴┴┘L2=”; L2; “└┴┴┘R2=”; R2 END Задача № 7( № 135) А) Составить программу вычисления значений функции Y=  Решение. Блок схема:  НАЧАЛО   ВВОД X,Y   X<=1  нет    -1 Y= sin 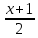 нет  sin         КОНЕЦ Вывод Y  - 1да Текст программы c использованием оператора условного перехода: CLS INPUT “X=”;X INPUT “Y=”Y IF x<=-1 THEN D = sin×(x+1)/2 ELSELF -1 D = x^2-1 ELSE D = sin( sqr(x-1) ENDIF PRINT “Y=”;Y END Б) Найти сумму числового ряда S=D1+D2+……+Dn С точностью eps=0.001. Составить блок-схему алгоритма и программу с использованием условного оператора. Суммирование закончить при выполнении условия │Dn│<=eps. 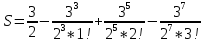 +……Рекомендуется при вычислении суммы S использовать рекуррентную формулу 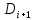 =  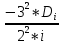,  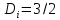Решение. Программа с использование условного оператора: CLS EPS = 0.001 EPS - точность D = 3/2 D – значение элемента ряда i = 3/2 i- номер элемента ряда S=0 S- сумма элементов ряда DO WHILE ABS(D) > EPS S = S+D i= i+1 D = -(3^2×D)/(2^2×i) LOOP   PRINT “S=”;S Выводим на экран сумму ряда, и номерPRINT “i=”;i последнего просуммированного элемента END ряда. Блок схема алгоритма:  НАЧАЛО       1 D=3/2 S=0 EPS = 0.001 i=3/2 1                  S,i D=(3/2 × D)/(2^2×i) i=i+1 S=S+D |D| <=EPS   КОНЕЦ Задача № 8(№155) А) Табулирование функции. Составить программу вычисления и печати функции Y при заданных значениях аргумента X=X1, X2, X3 …X50. Результат оформить в виде таблицы. Y= 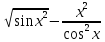 Решение Y= 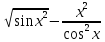CLS PRINT “X|Y”  FOR X=0 TO 5 STEP 0.1 Цикл повторяется 50 разY=SQR(ABS(sin(x^2))) – (x^2)/(cos(x)^2 PRINT USING “#.# | +##.###”; X;Y NEXT X END Блок – схема программы:               КОНЕЦ ВЫВОД X,Y Y=SQR(ABS(sin(x^2))) – (x^2)/(cos(x)^2 X = 0,5,0.1 НАЧАЛО Б) Составить блок-схему программу решения задачи с использованием оператора цикла. Найти среднее арифметическое от всех чётных отрицательных элементов вектора | Bk | (k = 1,10). Решение. | Bk | (k = 1,10) Блок – схема на следующей странице. CLS INPUT “N=”;N DIM A(N) FOR i=1 TO N INPUT “(k=1,10)”,A(i) PRINT “A(“;i;”) =”;A(i) NEXT i REM “Поиск среднего чётных элементов» S=0 : k=0 FOR i=1 TO 10 IF A(i)<0 : k = k+1 THEN NEXT i k: = k+1 s: = s + a[i] SR=S/k PRINT “Среднее значение”;SR END  НАЧАЛО 
    i=1,1                         КОНЕЦ ВЫВОД k k= k+1 k(i,j)<0 j=1,10 k=0 i=1,1 ВВОД k(i,j) j=1,10 Задача № 9(№175) Даны матрица A =|Ak,i| (k=1,5) и вектор B = |Bk| (k=1,5) Найти сумму элементов матрицы A, которые больше заданного числа M1, и меньше заданного числа M2. Решение: Зададим матрицу случайными числами.
Максимальное значение M1[1;5]= 40 Минимальное значение M2 [2;4]= - 25 Ввод данных в двумерный массив REM: DATA – READ INPUT “ Размерность N,M; N,M DIM A(N,M) DATA 2,-3,1,11,40,-8,5,0,-25,-7 FOR i=1 TO N FOR j=1 TO M READ A(i,j) NEXT j NEXT Решение. CLS DIM A(5,5) DATA 2,-3,1,11,40 DATA -8,5,0,-25,-7 DATA 7,-14,4,-3,0 DATA -9,13,6,10,-1 DATA 12,0,30,-5,20 FOR k=1 TO 5 FOR i=1 TO 5 READ A(k;i) NEXT i NEXT k Контроль “ Распечатка матрицы” PRINT “Матрица A” FOR k=1 TO 5 FOR i=1 TO 5 PRINT A(k;i) NEXT i NEXT k Блок – схема на следующей странице. Блок- схема  НАЧАЛО  A(5,5) Обьявление массива                              1 ВЫВОД A(k,i) ВВОД A(k;i) i=1,5 k(1,5) i=1,5 k=1,5 Нахождение суммы элементов больше М1, и меньше M2 Составление программы, с использованием оператора условного перехода CLS WRITELN( ‘ Сколько элементов в 5 столбце <= 10?’) N:=0 FOR i:=1 TO 5 do1 IF A [i,5]; A(i,i) <=M2; => M1 THEN n:=n+1 NEXT i PRINT “N =”;N END Блок – схема алгоритма:  1      A(I,i) <= M2; => M1 i=1,5 n=0      -       КОНЕЦ ВЫВОД n n=n+1 + |