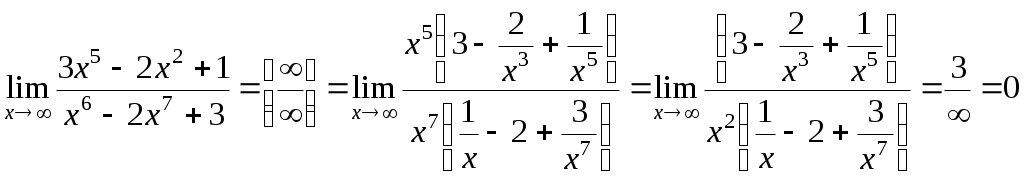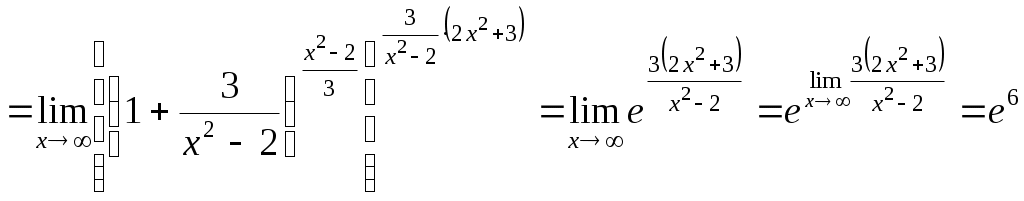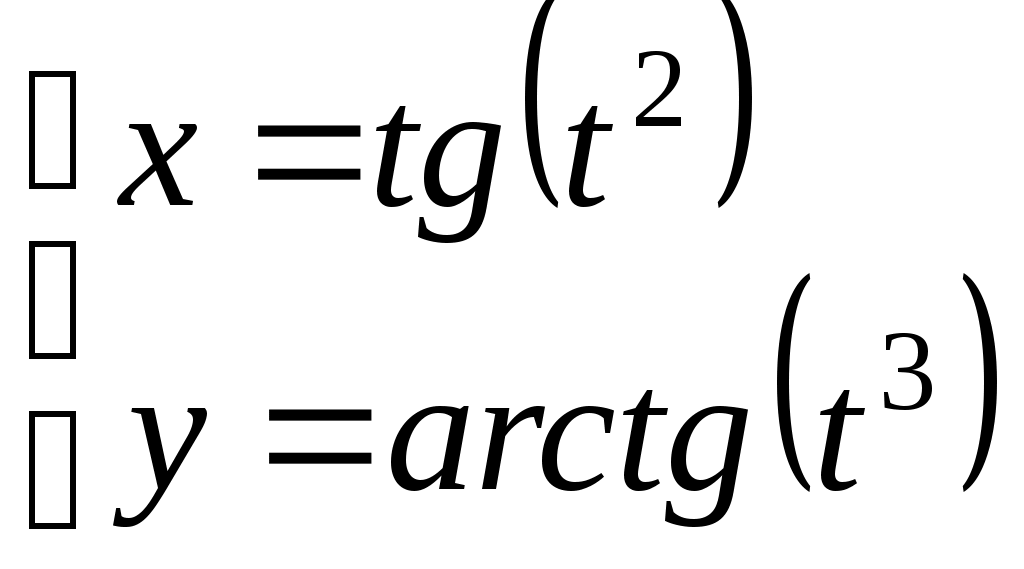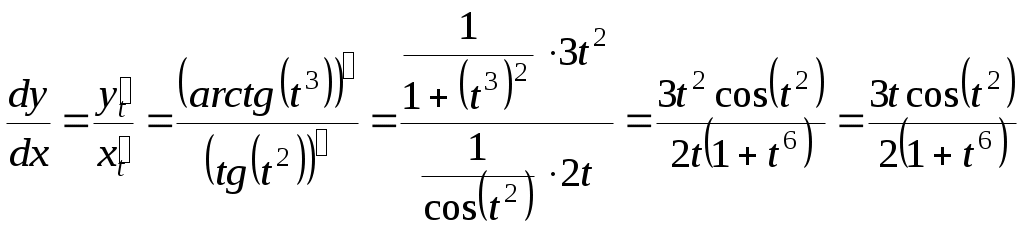|
Контрольная работа_Павлов.М.Д. Контрольная работа 1 Задача Заданы матрицы А, В, С. Найти а б вычислить определитель матрицы А
Контрольная работа № 2
1.6.5. Даны вершины пирамиды 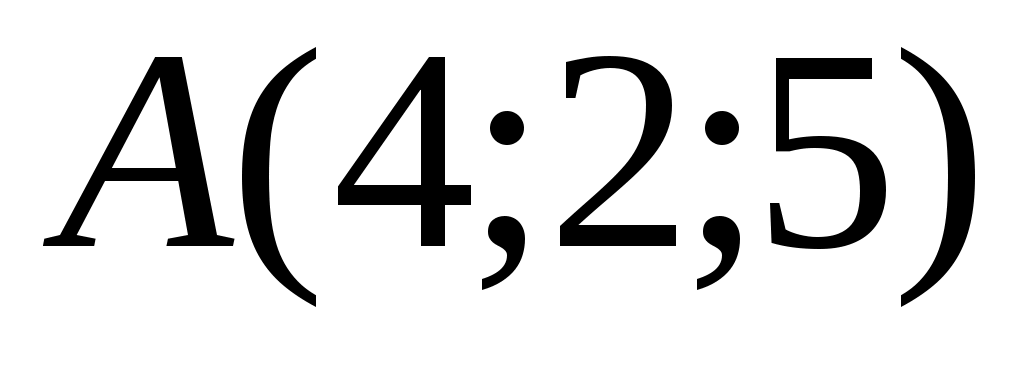 , , 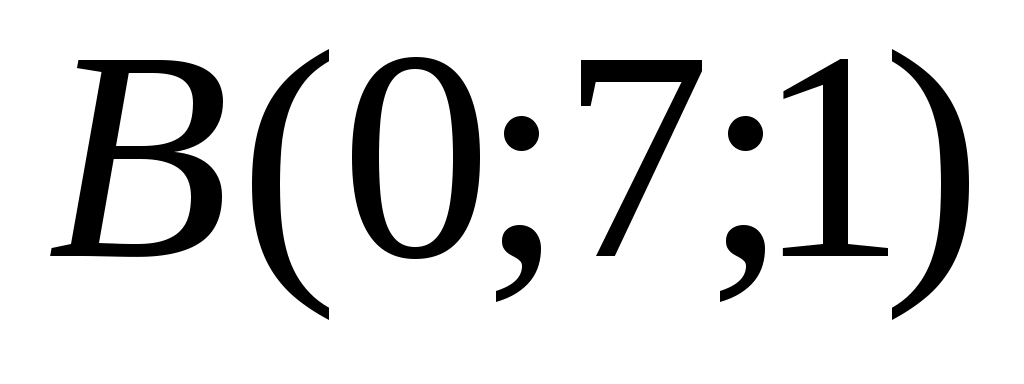 , , 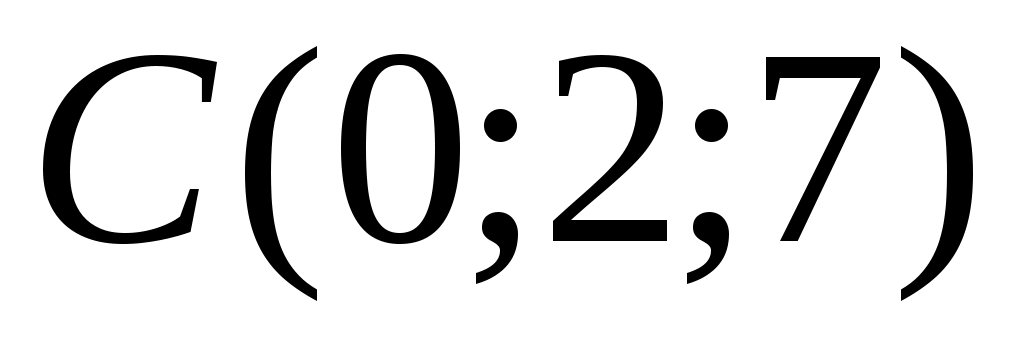 , , 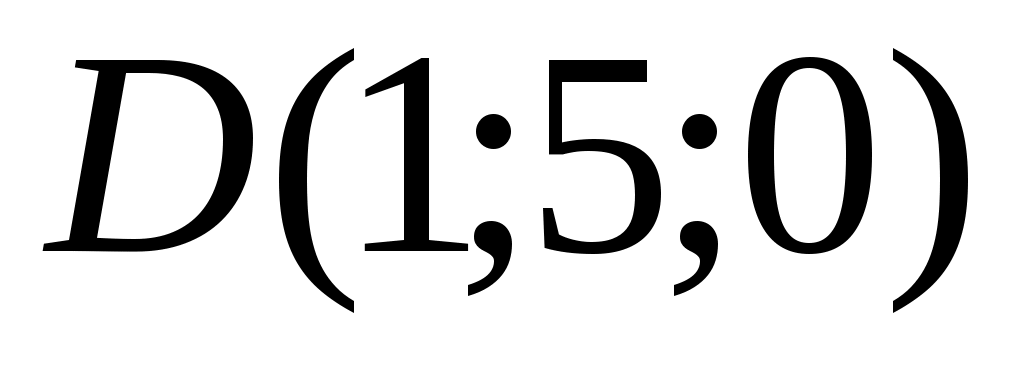 . Найти: а) угол между гранями . Найти: а) угол между гранями 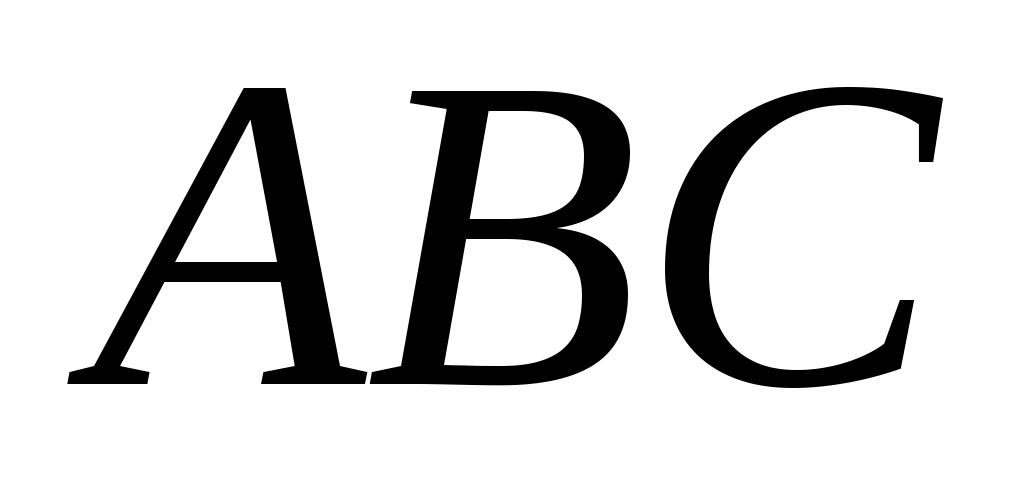 и и 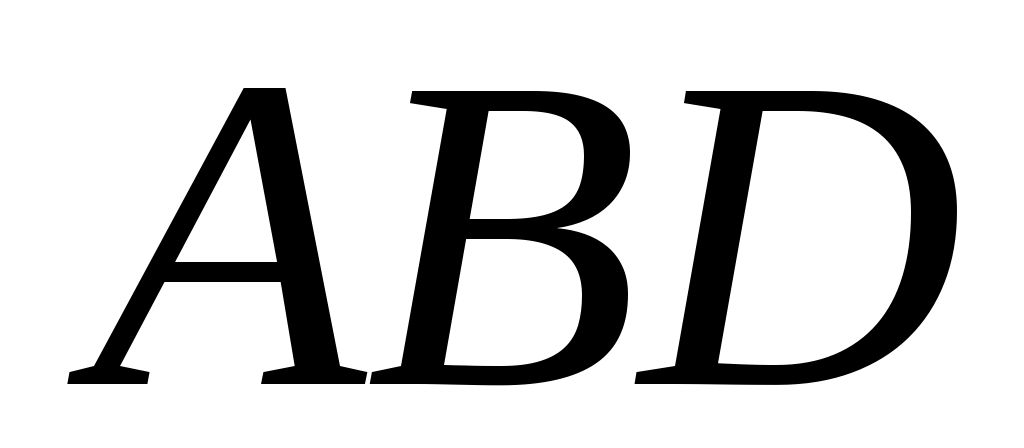 ; б) каноническое и параметрические уравнения прямой ; б) каноническое и параметрические уравнения прямой  ; в) уравнение плоскости параллельной плоскости ; в) уравнение плоскости параллельной плоскости 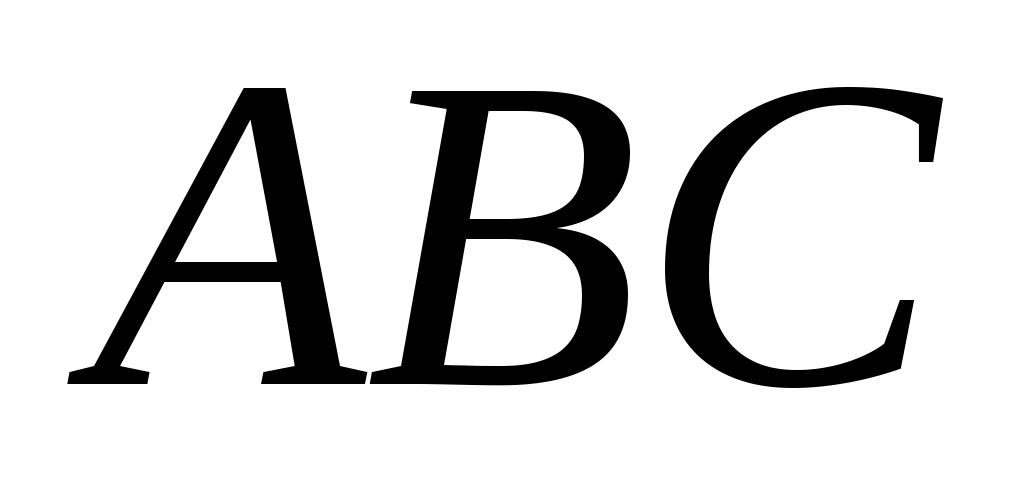 , проходящей через точку , проходящей через точку 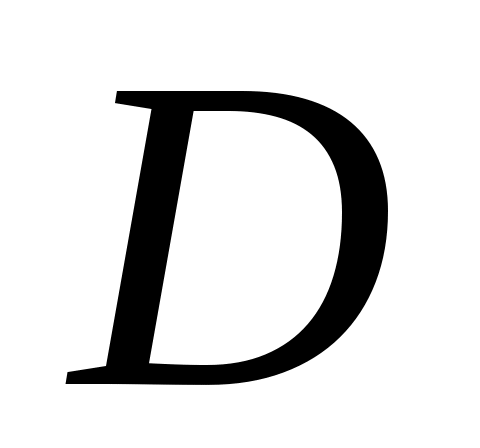 ; г) каноническое уравнение высоты пирамиды. ; г) каноническое уравнение высоты пирамиды.
а) Косинус угла между двумя плоскостями 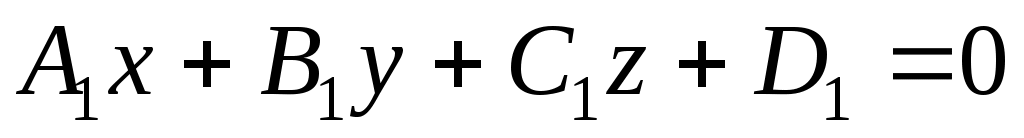 и и 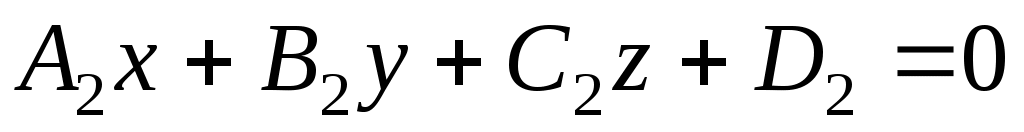 вычислим по формуле: вычислим по формуле:
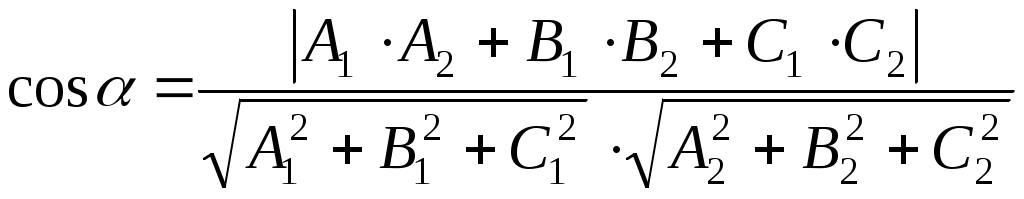 . .
Составим уравнение плоскости  . Уравнение плоскости, проходящей через три точки . Уравнение плоскости, проходящей через три точки 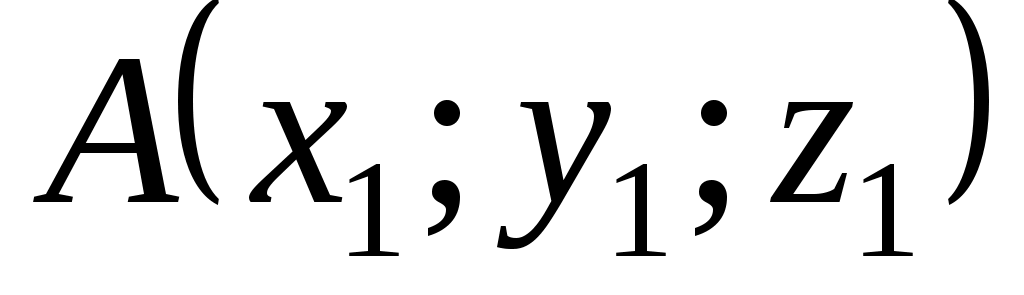 , , 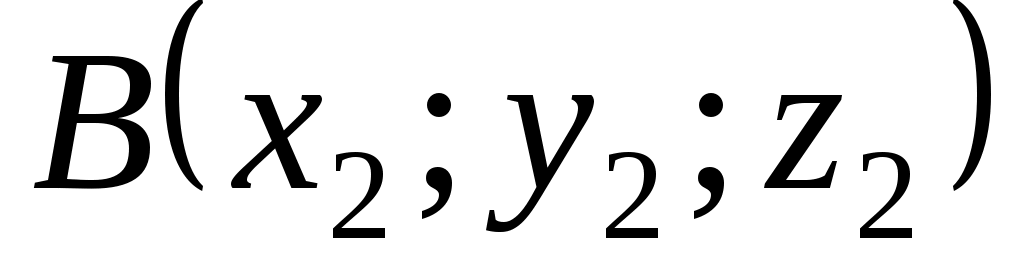 , , 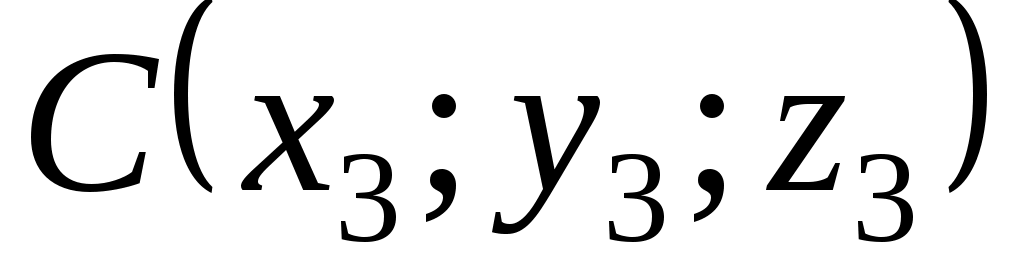 найдем по формуле: найдем по формуле: 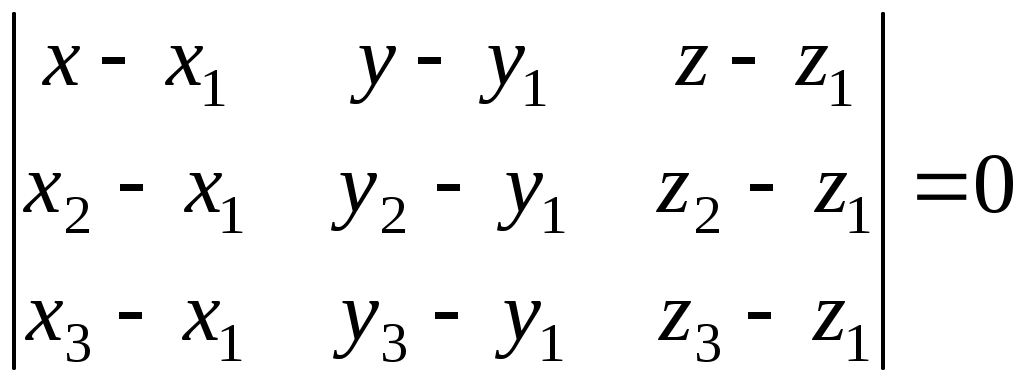 . .
Подставляя соответствующие координаты точек 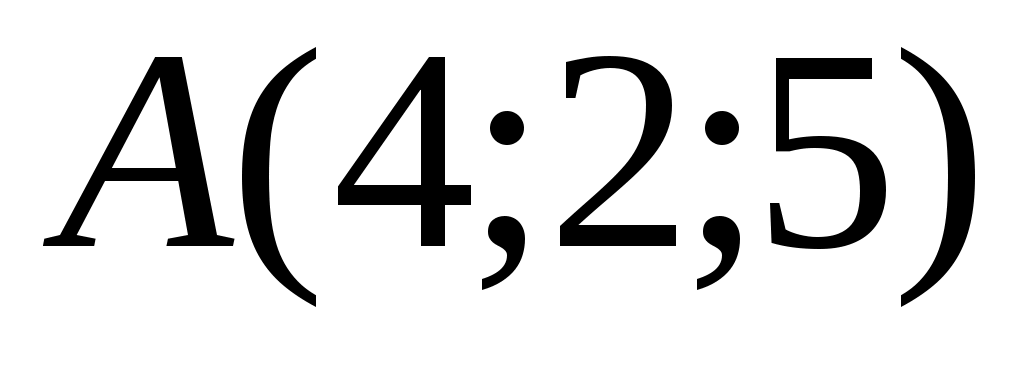 , , 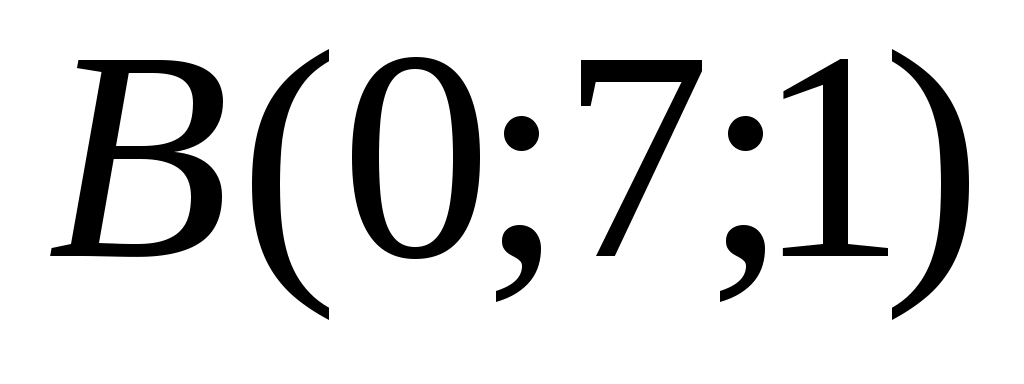 , , 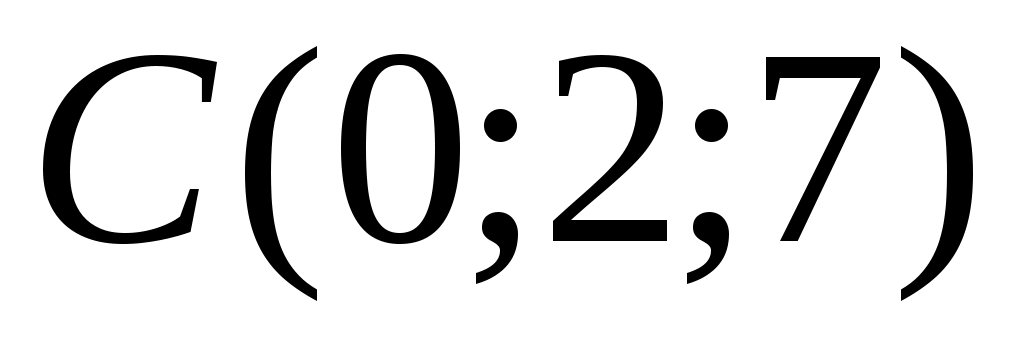 , получим: , получим:
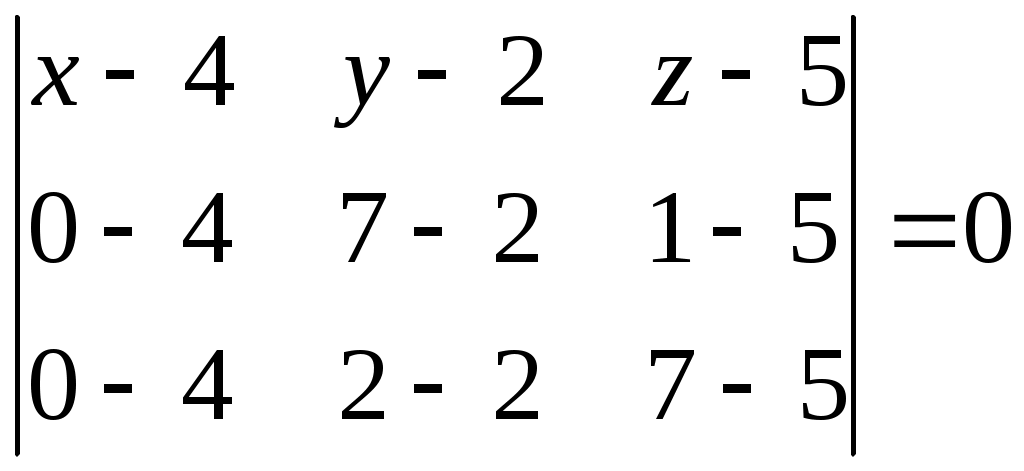 ; ; 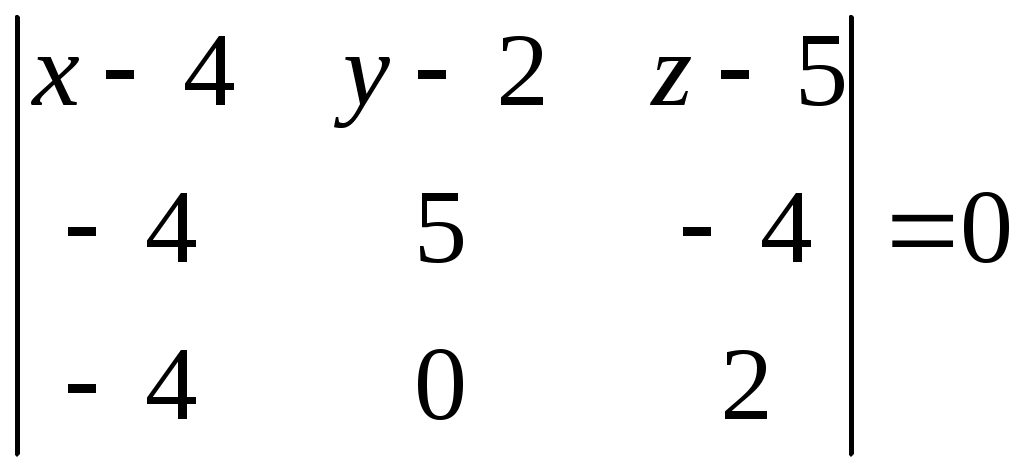 ; ;
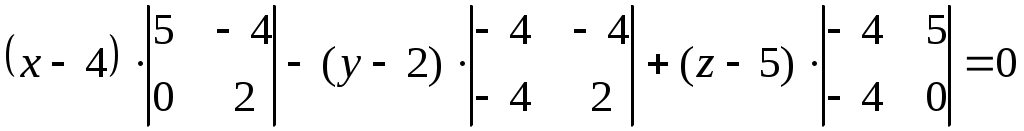 ; ;
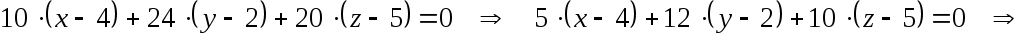
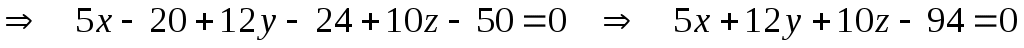
Таким образом, уравнение грани 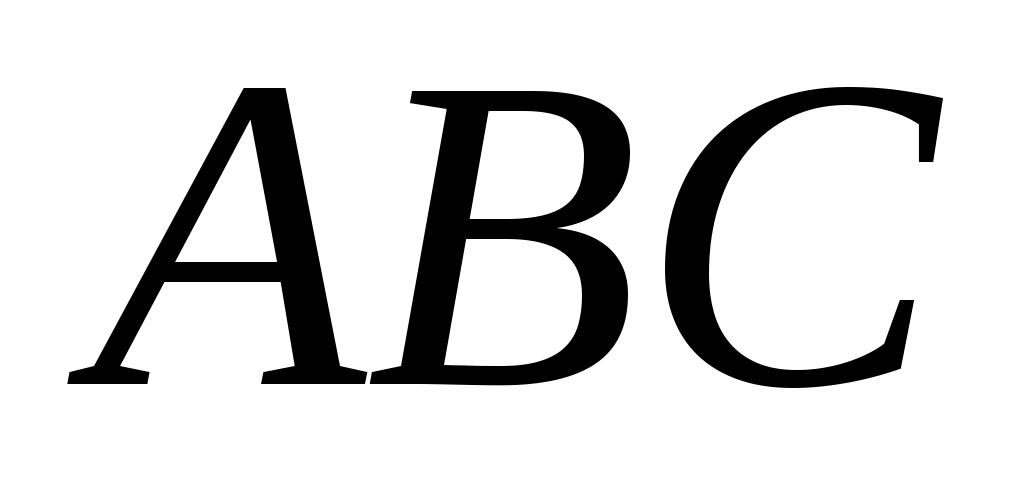 : : 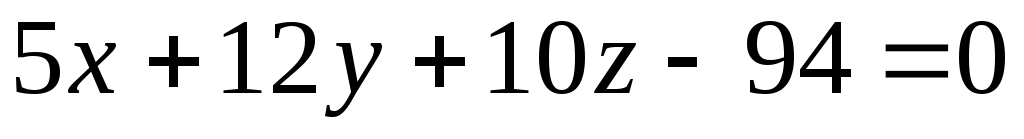 . .
Составим уравнение плоскости 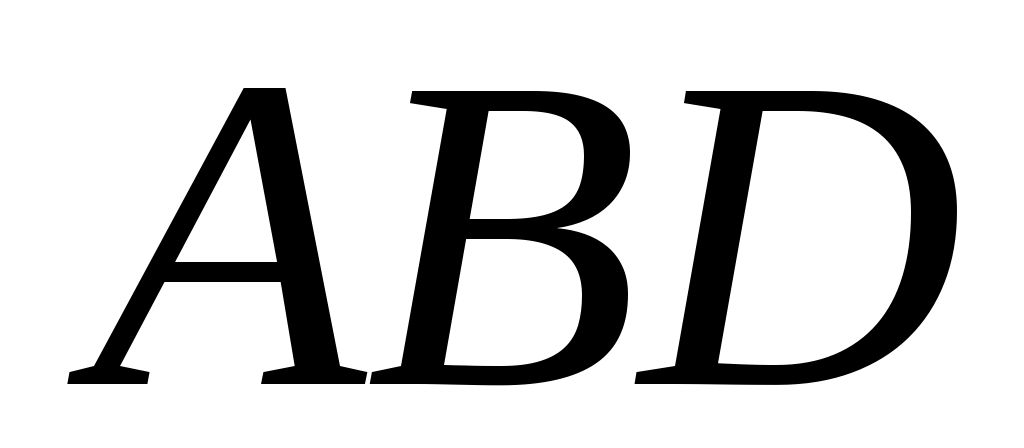 , проходящей через три точки , проходящей через три точки 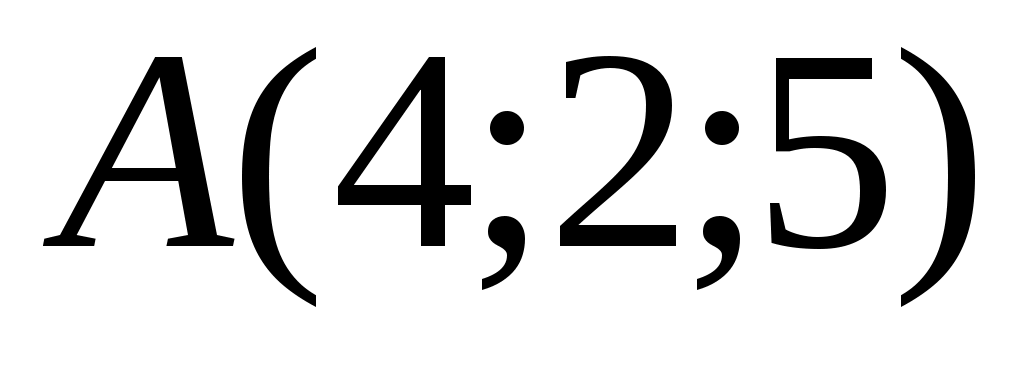 , , 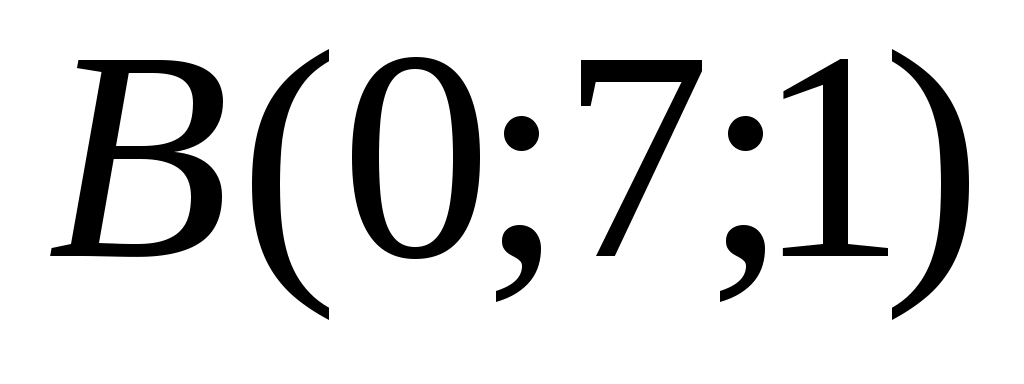 и и 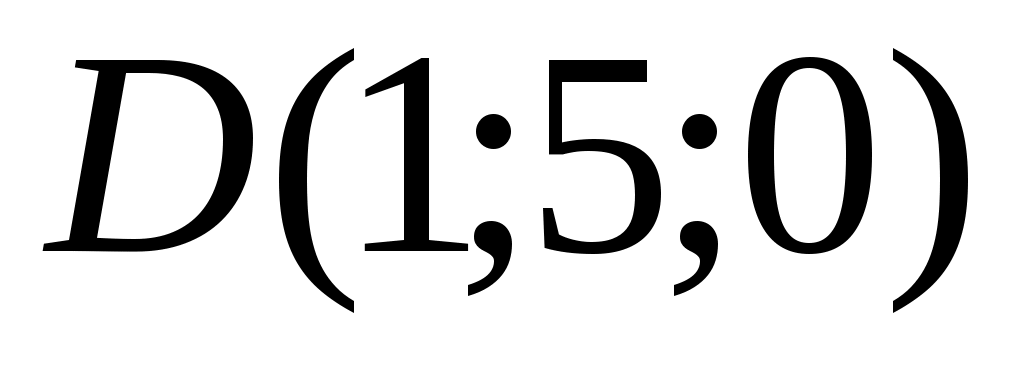 : :
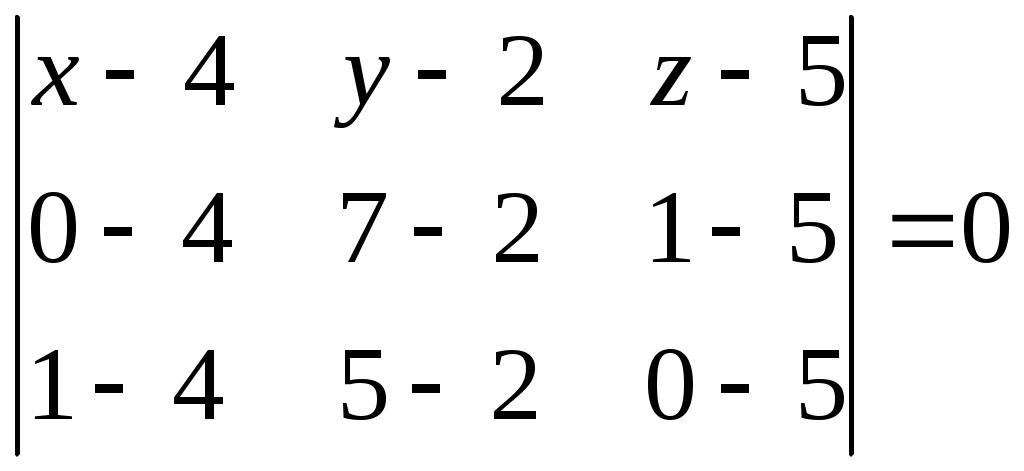 ; ; 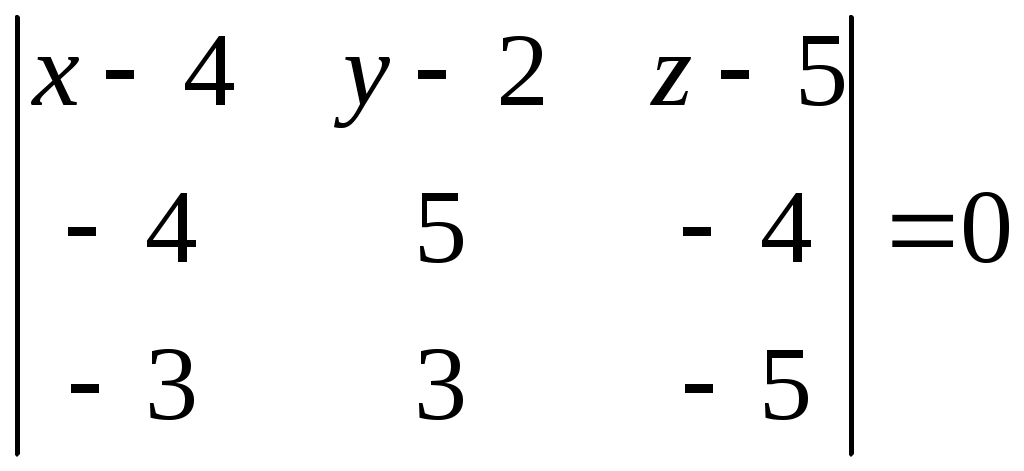 ; ;
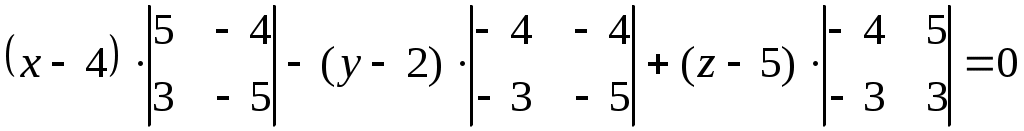 ; ;
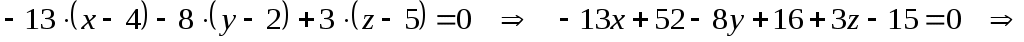
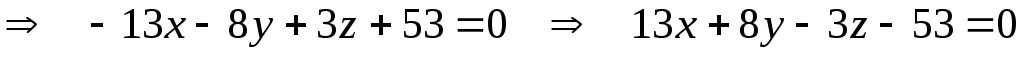
Таким образом, уравнение плоскости  : : 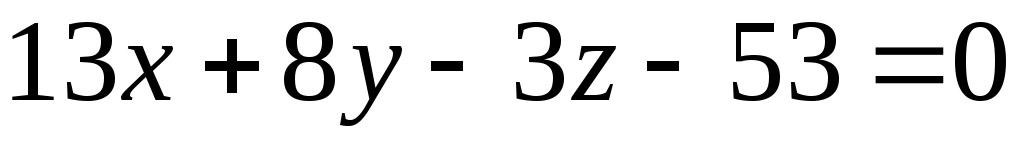
Тогда, подставляя в формулу для вычисления косинуса угла между плоскостями соответствующие значения, получим:
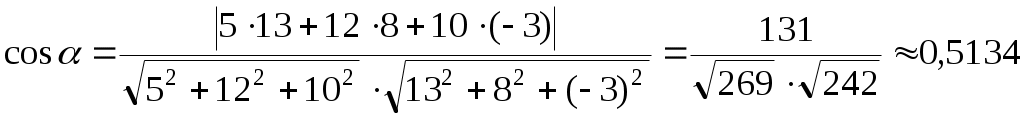 . .
Следовательно, 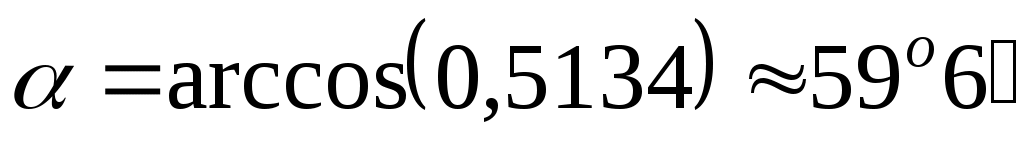 . .
б) Канонические уравнения прямой, проходящей через две точки пространства 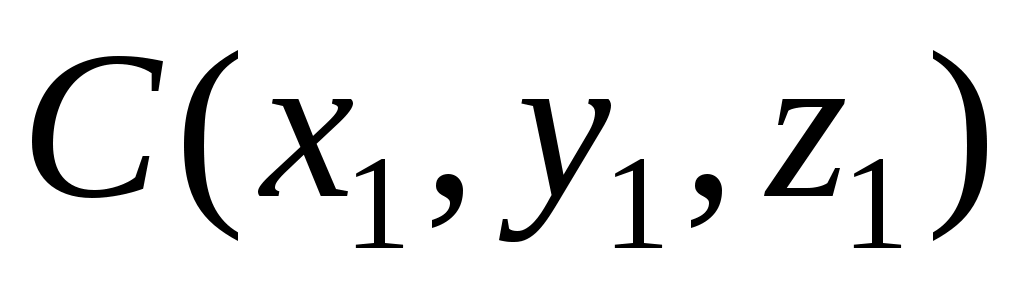 и и 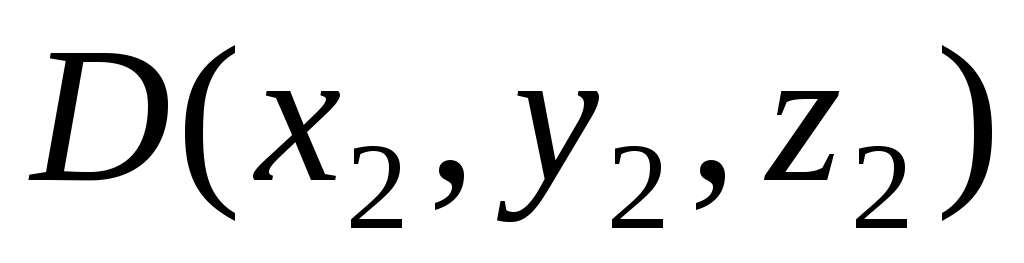 , имеют вид: , имеют вид:
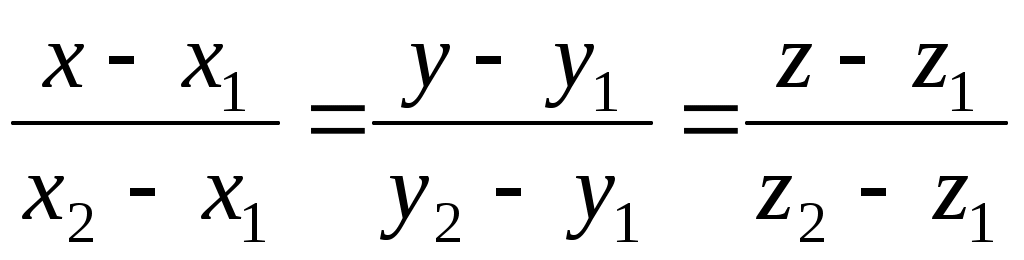 . .
Подставляя соответствующие координаты точек 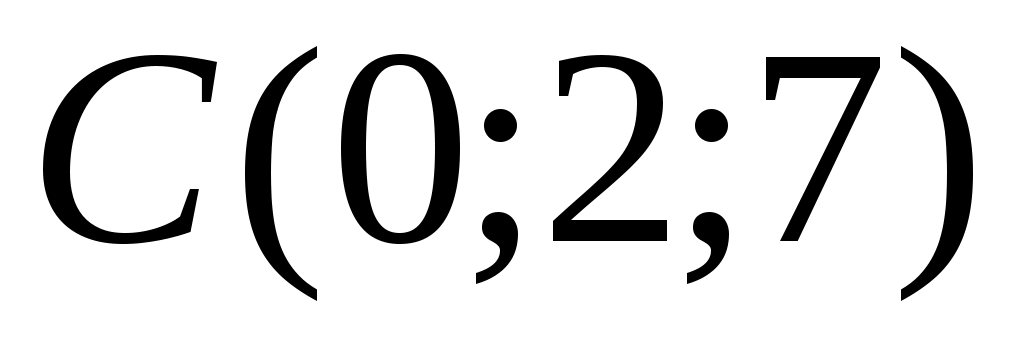 и и 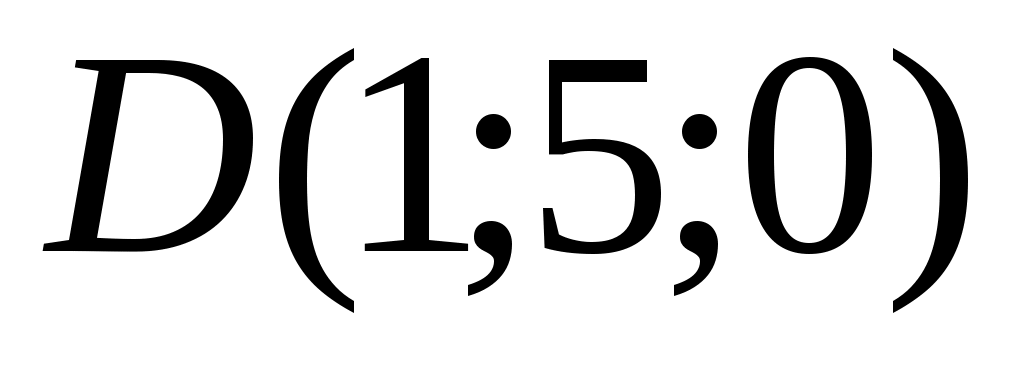 , запишем канонические уравнения прямой , запишем канонические уравнения прямой  : :
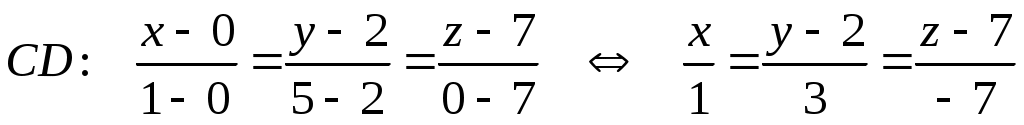 . .
Приравняв каждую часть из канонических уравнений прямой к параметру  , получим параметрические уравнения: , получим параметрические уравнения:
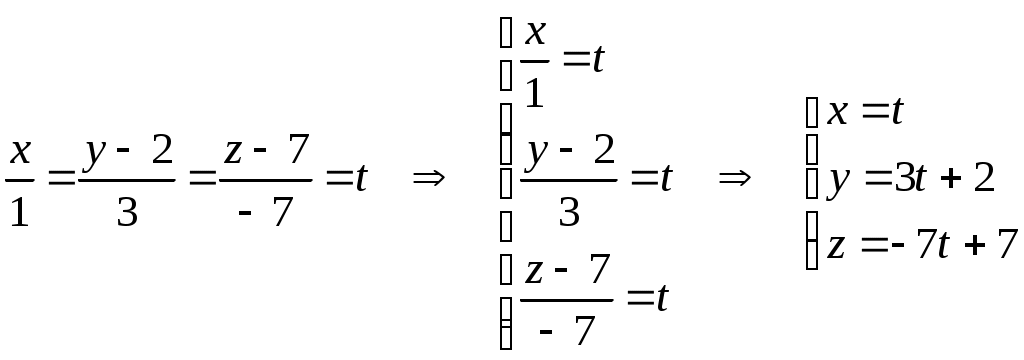 . .
в) Очевидно, вектор 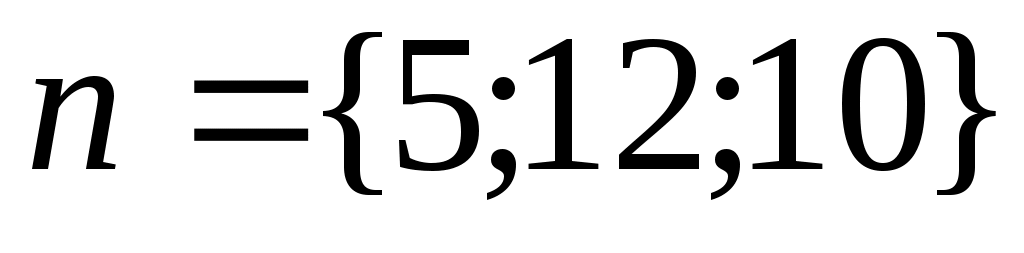 есть нормальный вектор плоскости есть нормальный вектор плоскости  : : 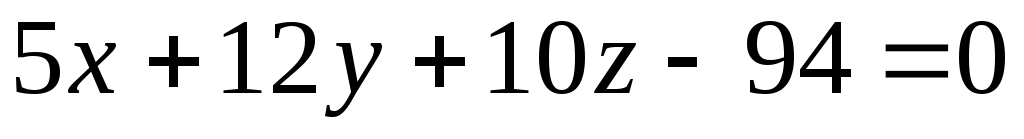 . Так как плоскость, уравнение которой мы ищем, параллельна плоскости . Так как плоскость, уравнение которой мы ищем, параллельна плоскости  , то ее нормальным вектором так же будет вектор , то ее нормальным вектором так же будет вектор 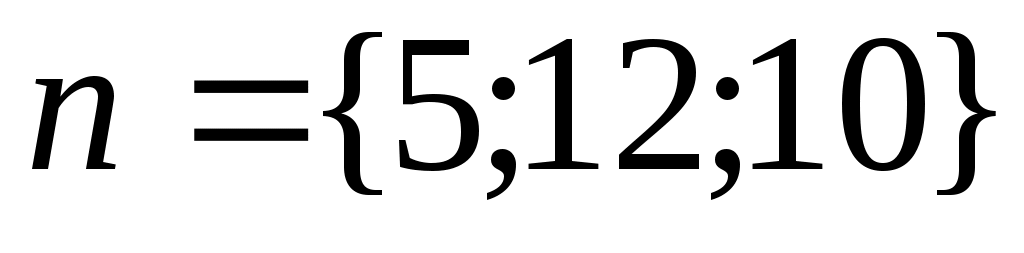 . Уравнение плоскости, которая проходит через точку . Уравнение плоскости, которая проходит через точку 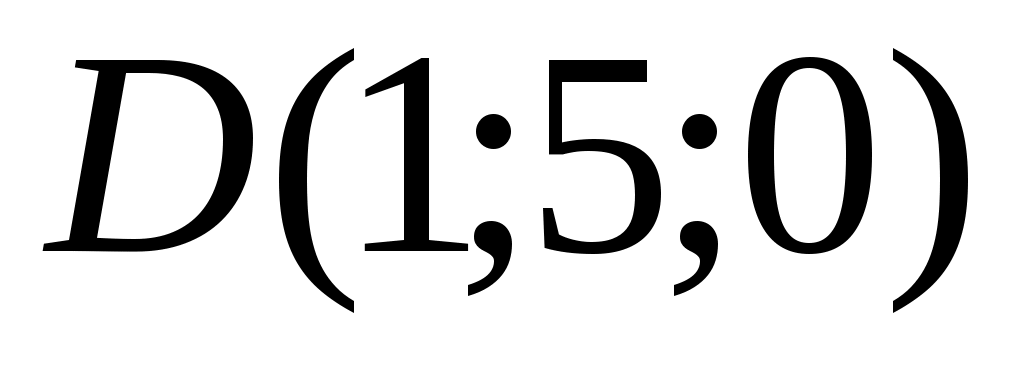 и имеет нормальный вектор и имеет нормальный вектор 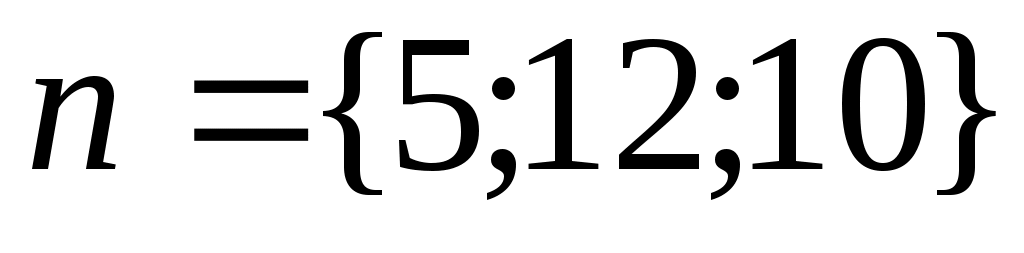 , имеет вид , имеет вид
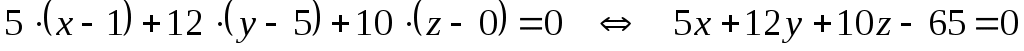
Это и есть искомое уравнение плоскости, проходящей через заданную точку 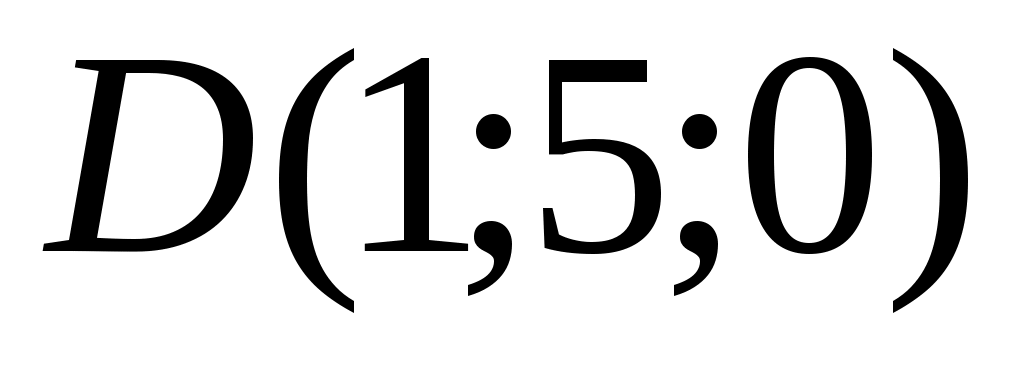 параллельно плоскости параллельно плоскости  . .
г) Так как высота, опущенная из вершины  перпендикулярна плоскости перпендикулярна плоскости  : :  , то направляющим вектором искомой высоты возьмем нормальный вектор плоскости, т.е. , то направляющим вектором искомой высоты возьмем нормальный вектор плоскости, т.е. 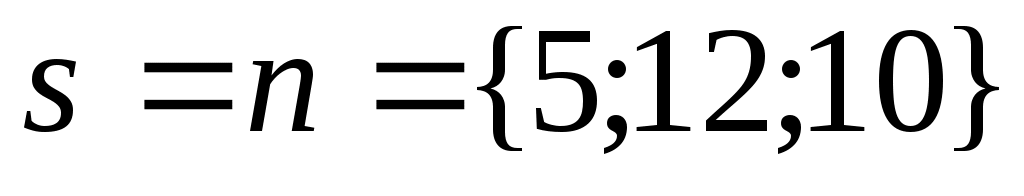 . Тогда канонические уравнения прямой, которая проходит через точку . Тогда канонические уравнения прямой, которая проходит через точку 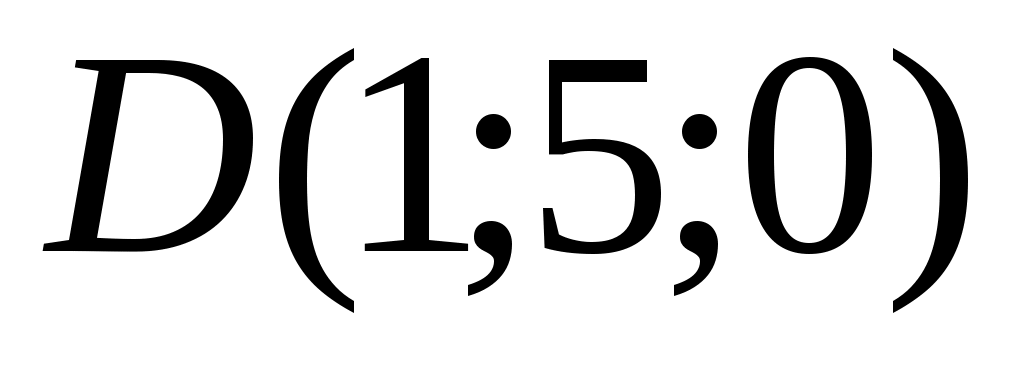 и имеет направляющий вектор и имеет направляющий вектор 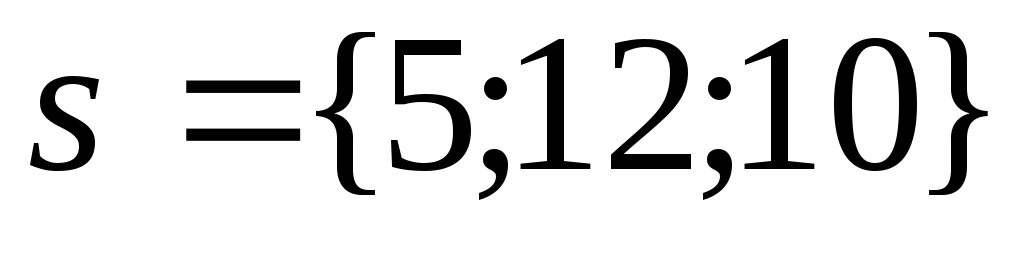 , будут иметь вид: , будут иметь вид:
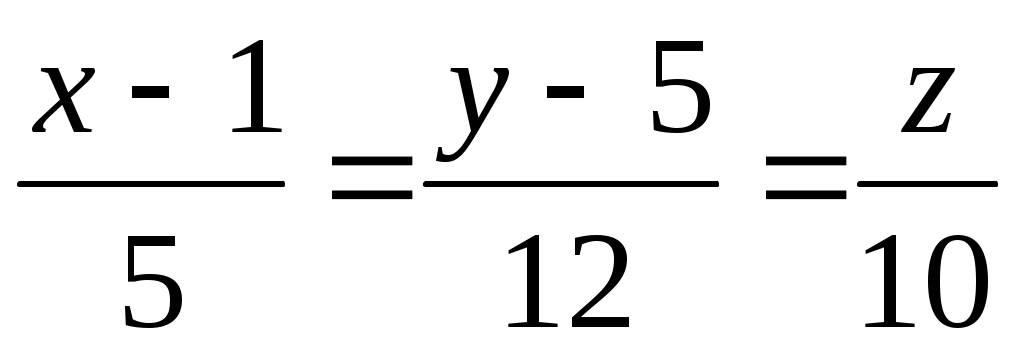 . .
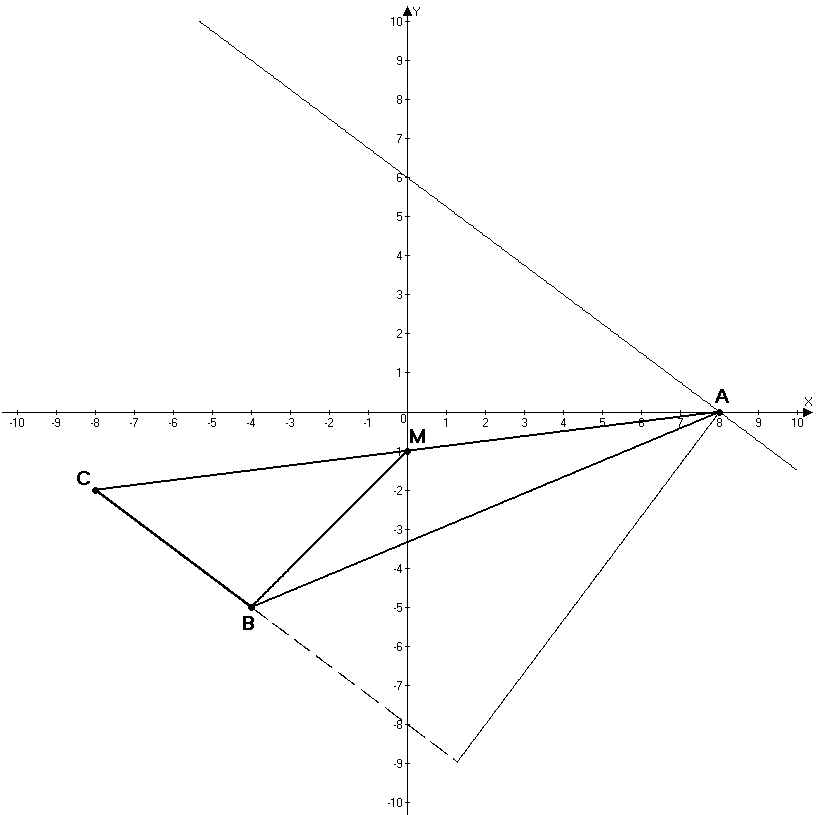
1.7.5. Даны три точки на плоскости: 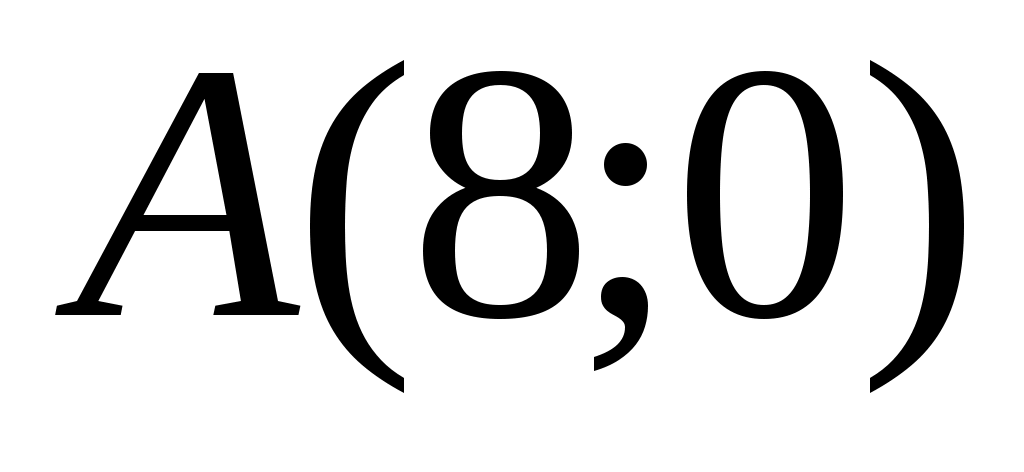 , , 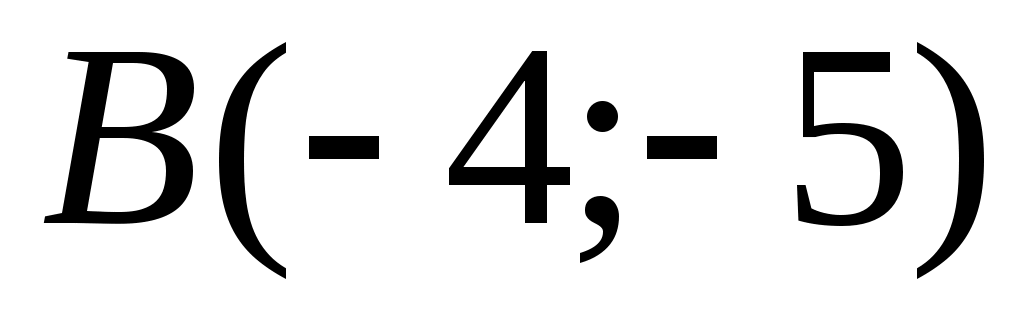 , , 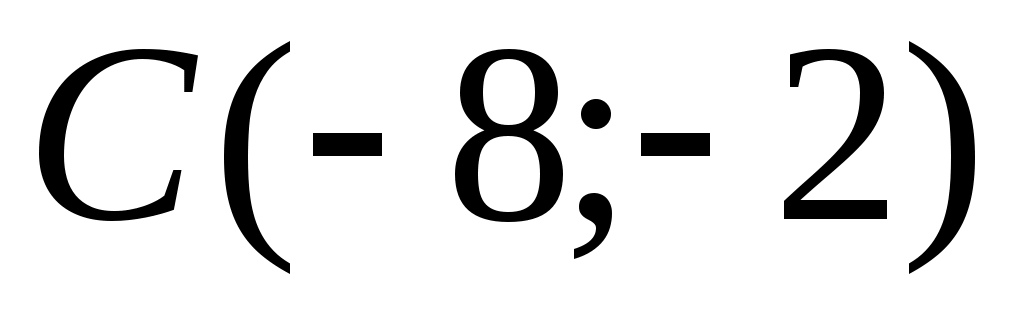 . Найти: а) уравнение стороны . Найти: а) уравнение стороны 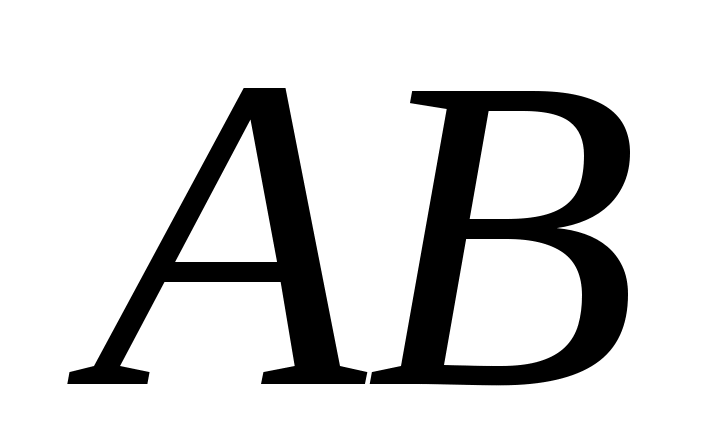 ; б) уравнение высоты, опущенной из вершины ; б) уравнение высоты, опущенной из вершины  ; в) уравнение медианы, опущенной из вершины ; в) уравнение медианы, опущенной из вершины 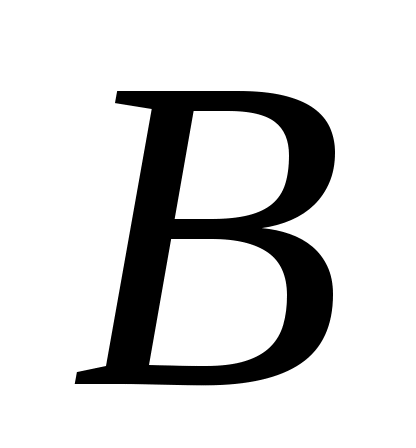 ; г) уравнение прямой, параллельной прямой ; г) уравнение прямой, параллельной прямой 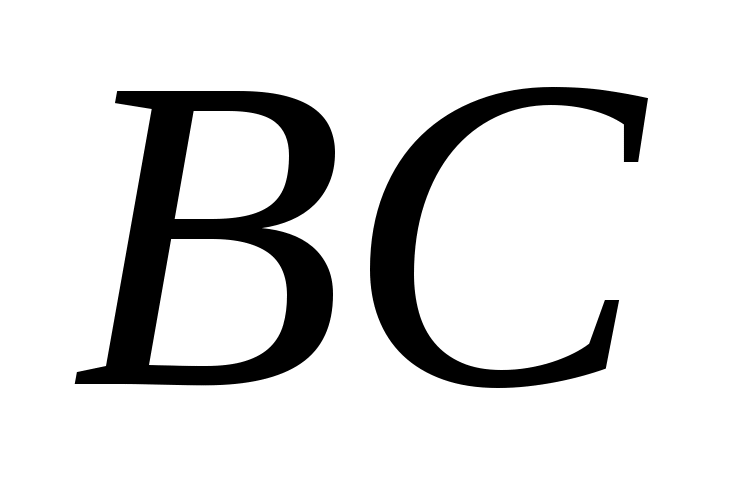 , проходящей через точку , проходящей через точку  ; д) угол при вершине ; д) угол при вершине 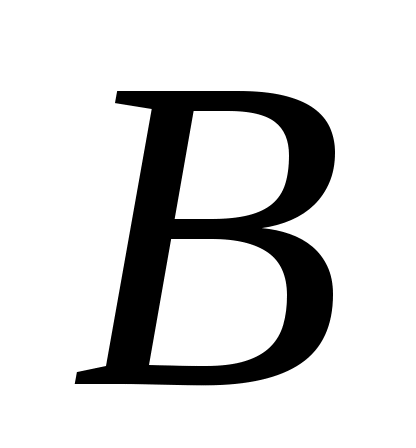 . Сделать чертеж . Сделать чертеж
а) Каноническое уравнение прямой, проходящей через две точки плоскости 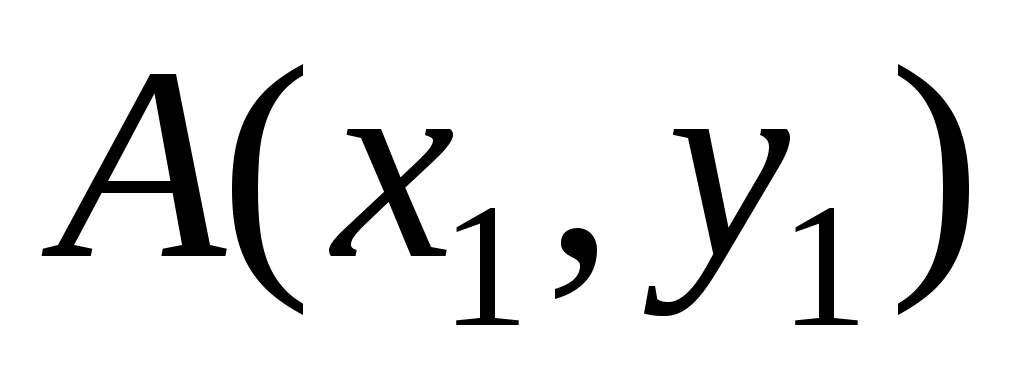 и и 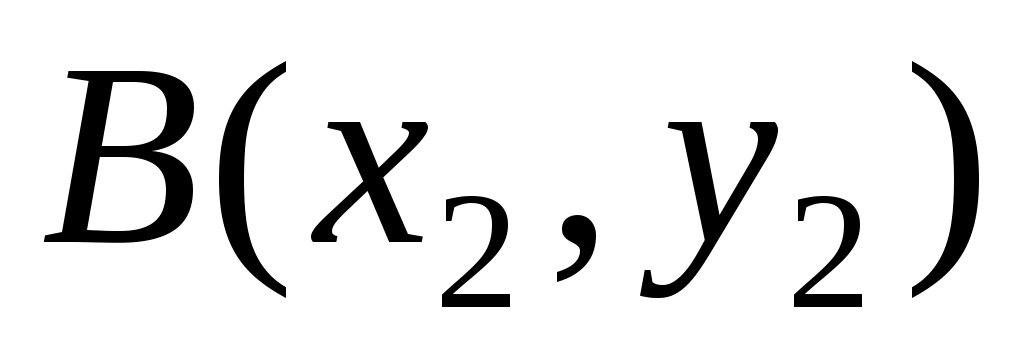 , имеет вид: , имеет вид:
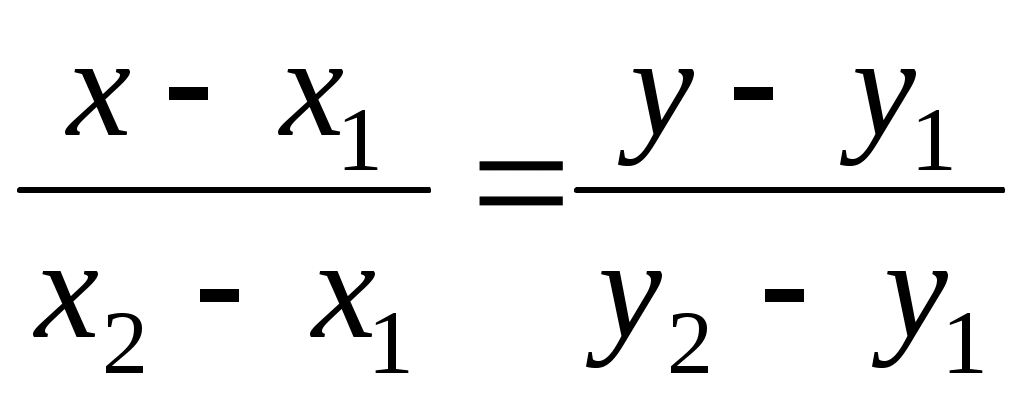 . .
Подставляя соответствующие координаты точек 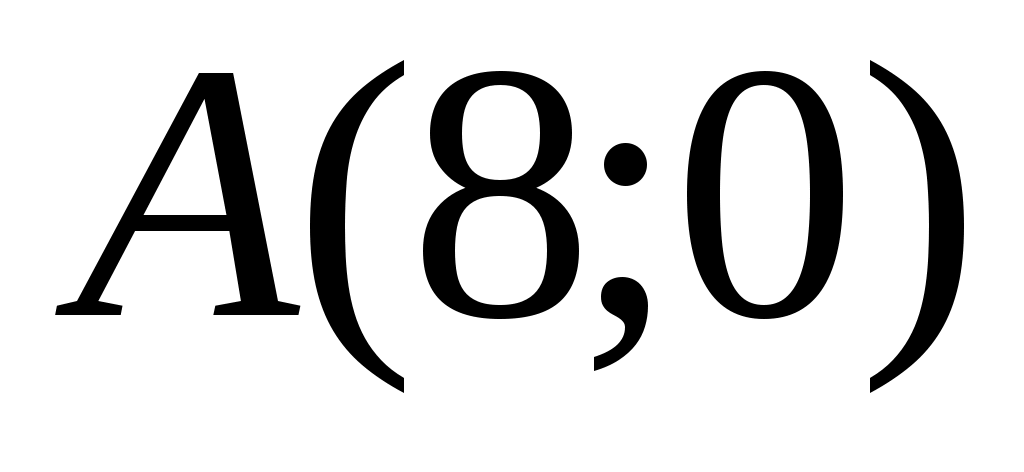 и и 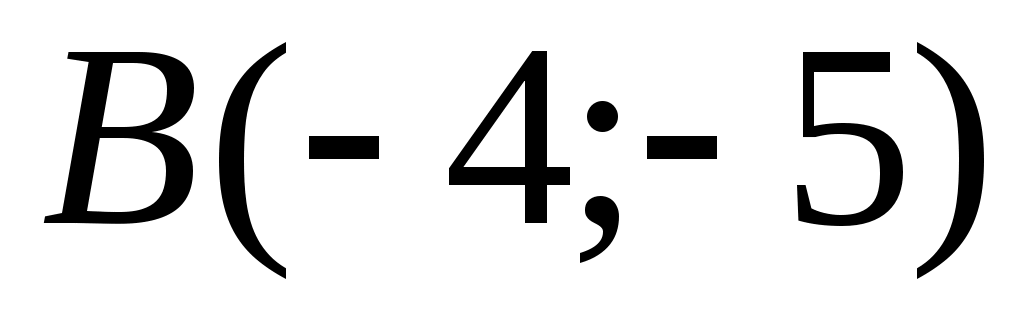 , запишем каноническое уравнение стороны , запишем каноническое уравнение стороны  : :
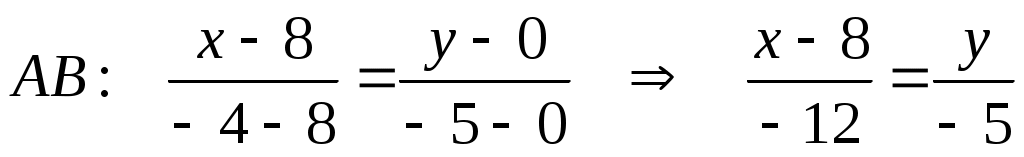
б) Запишем каноническое уравнение стороны  : : 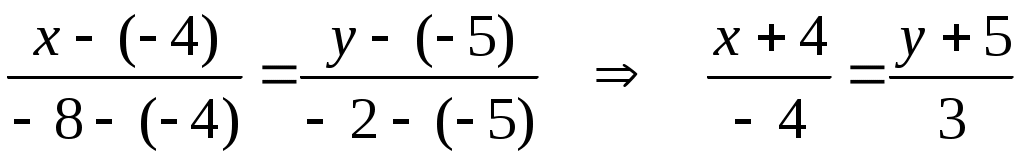 и представим его в виде с угловым коэффициентом: и представим его в виде с угловым коэффициентом: 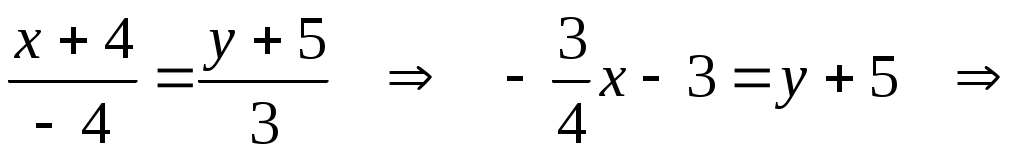 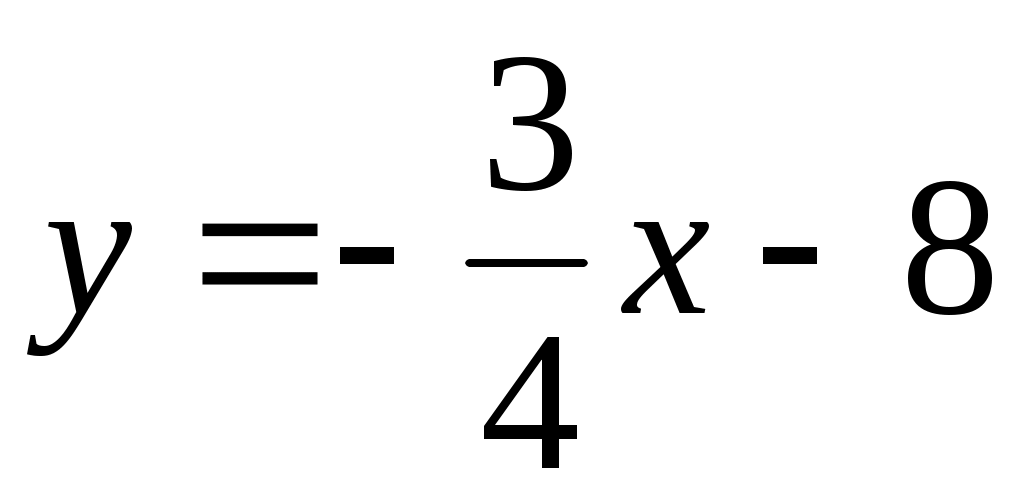 . Следовательно, угловой коэфф. прямой . Следовательно, угловой коэфф. прямой 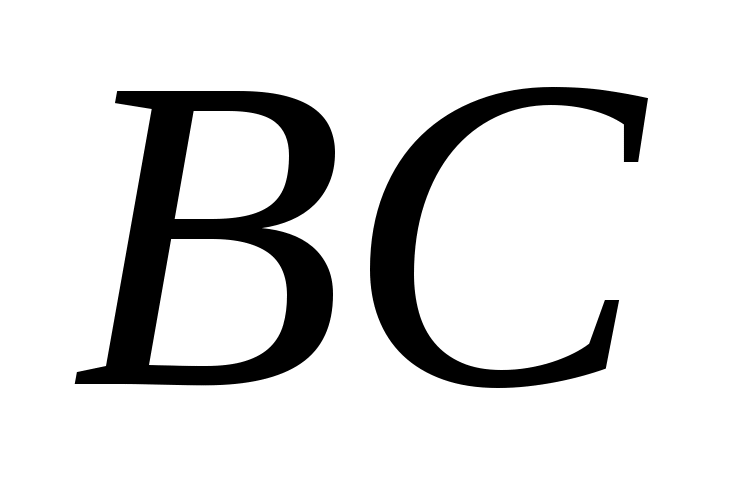 равен равен 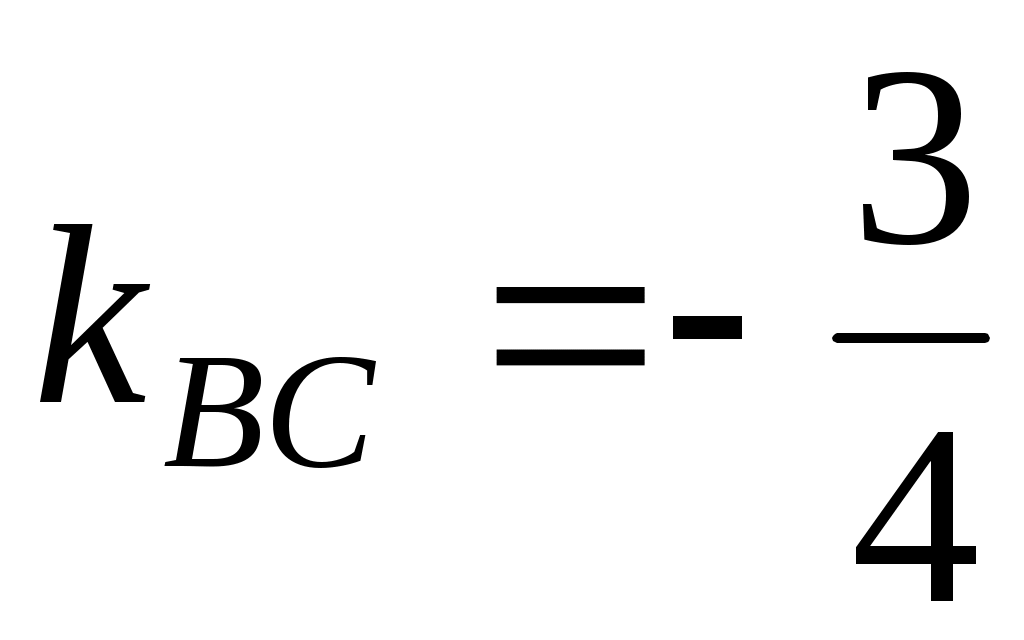 . .
Поскольку искомая высота перпендикулярна 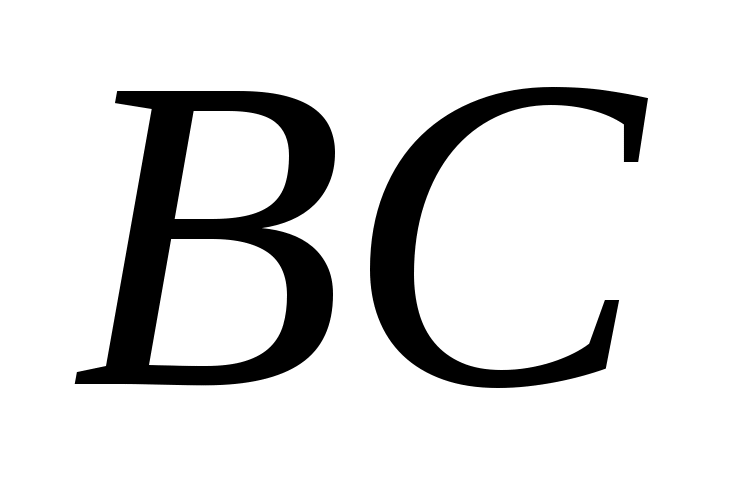 , то ее угловой коэффициент будет равен , то ее угловой коэффициент будет равен 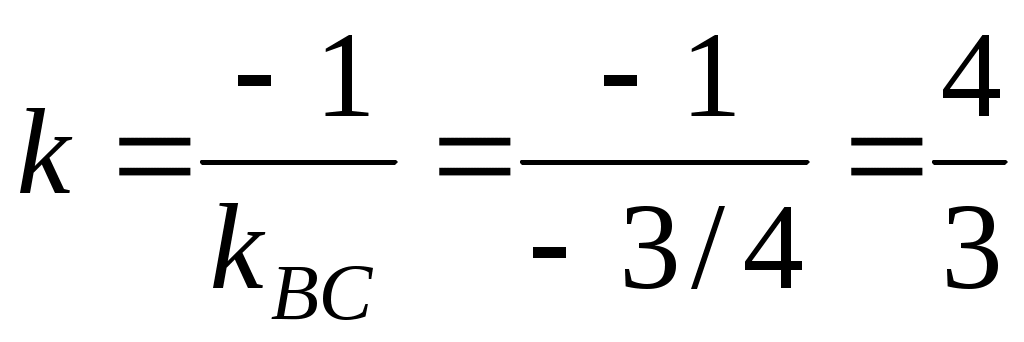 . По условию, искомая высота проходит через точку . По условию, искомая высота проходит через точку 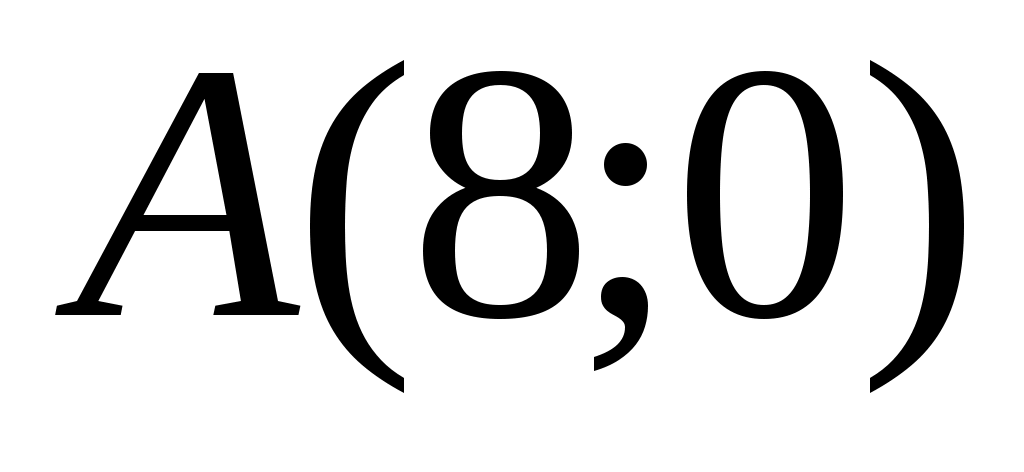 , значит, ее уравнение будет иметь вид: , значит, ее уравнение будет иметь вид:
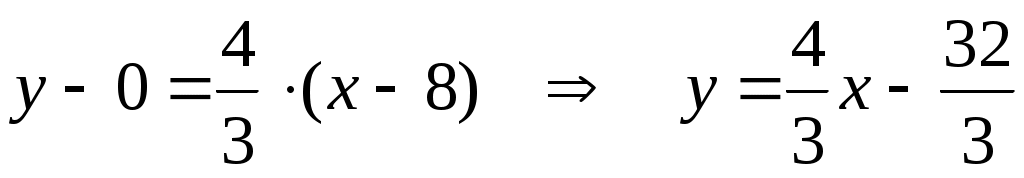 . .
в) Поскольку 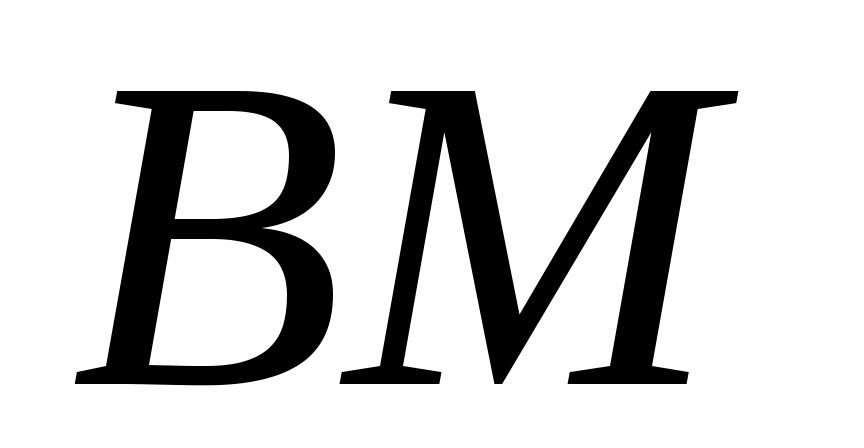 медиана, то точка медиана, то точка 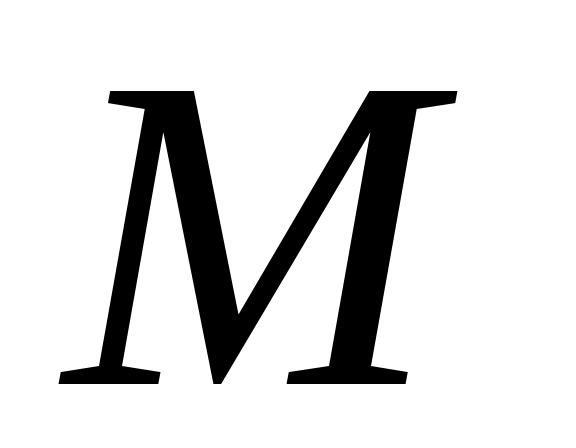 является серединой стороны является серединой стороны 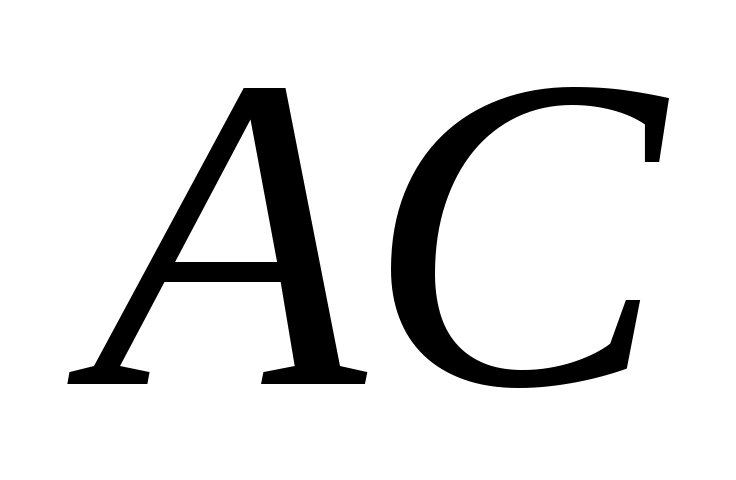 . Найдем ее координаты: . Найдем ее координаты:
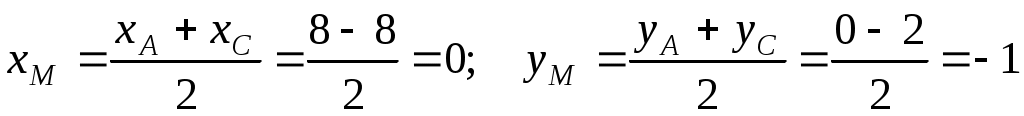
Теперь запишем уравнение медианы 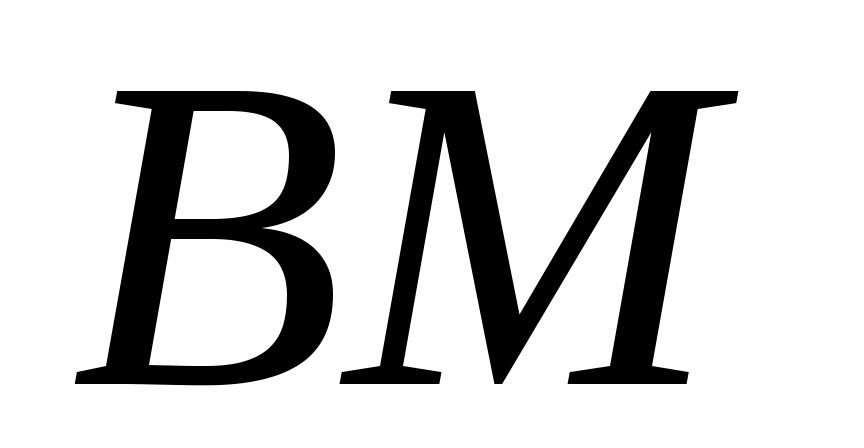 как уравнение прямой, проходящей через две точки как уравнение прямой, проходящей через две точки 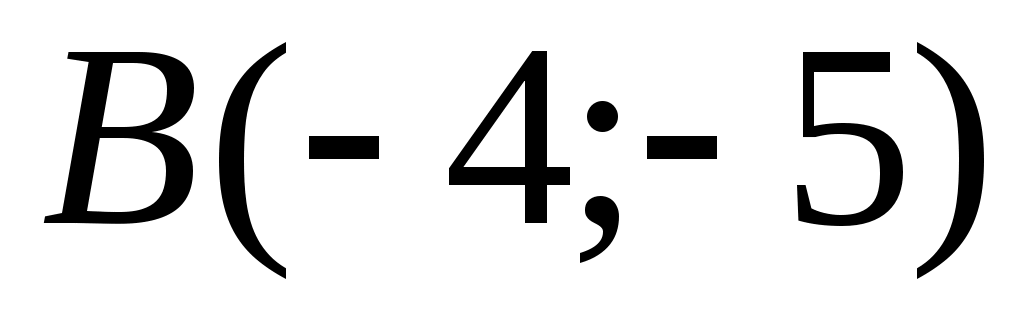 и и 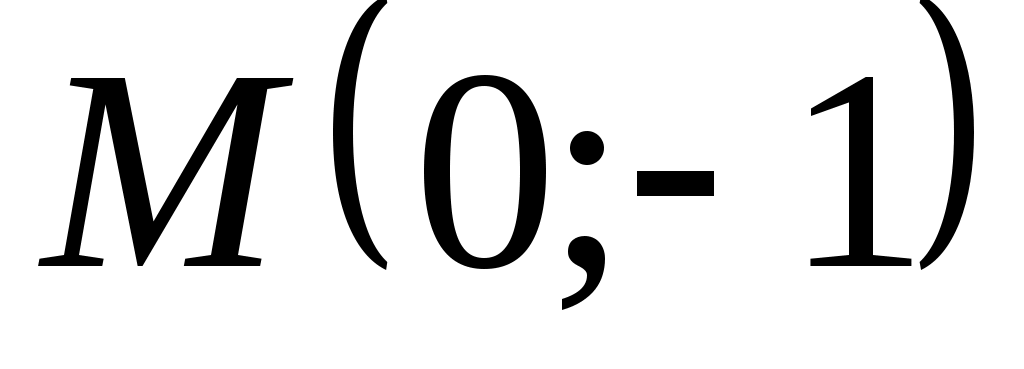 : :
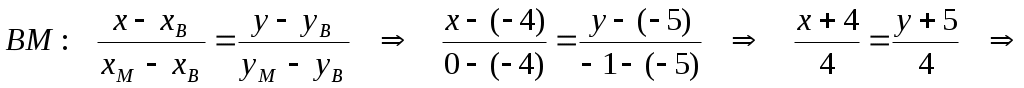
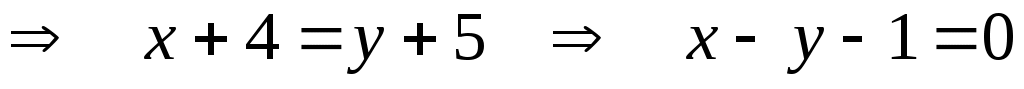
г) Угловой коэфф. прямой 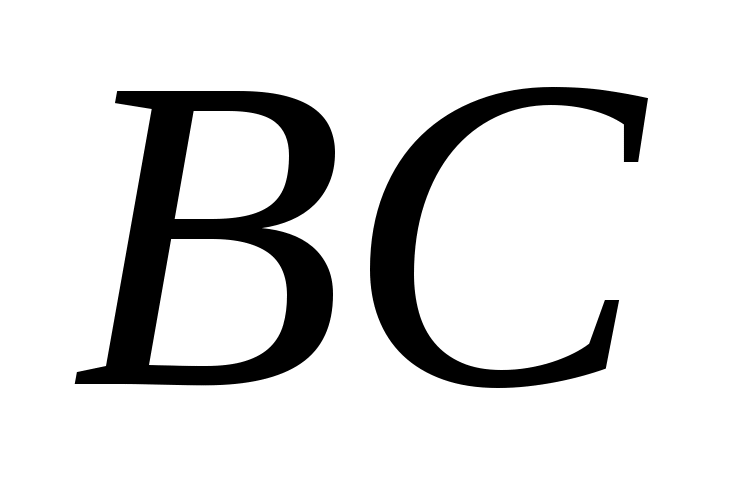 равен равен 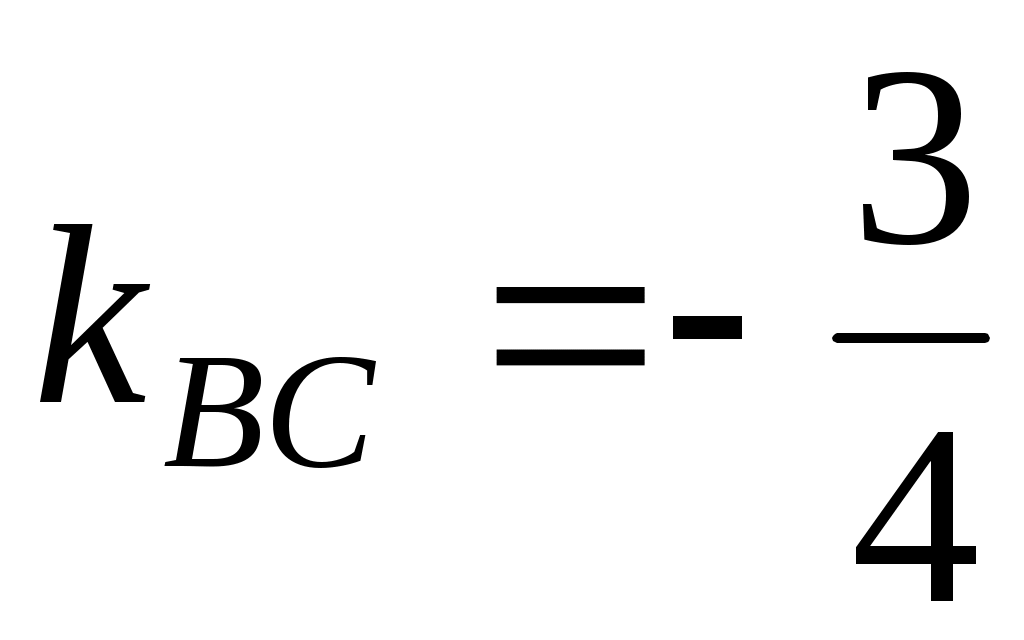 . Поскольку искомая прямая параллельна . Поскольку искомая прямая параллельна 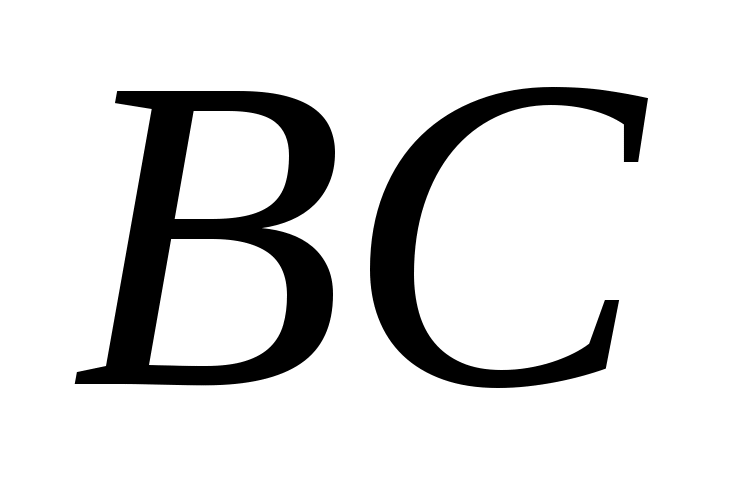 , то ее угловой коэффициент также будет равен , то ее угловой коэффициент также будет равен 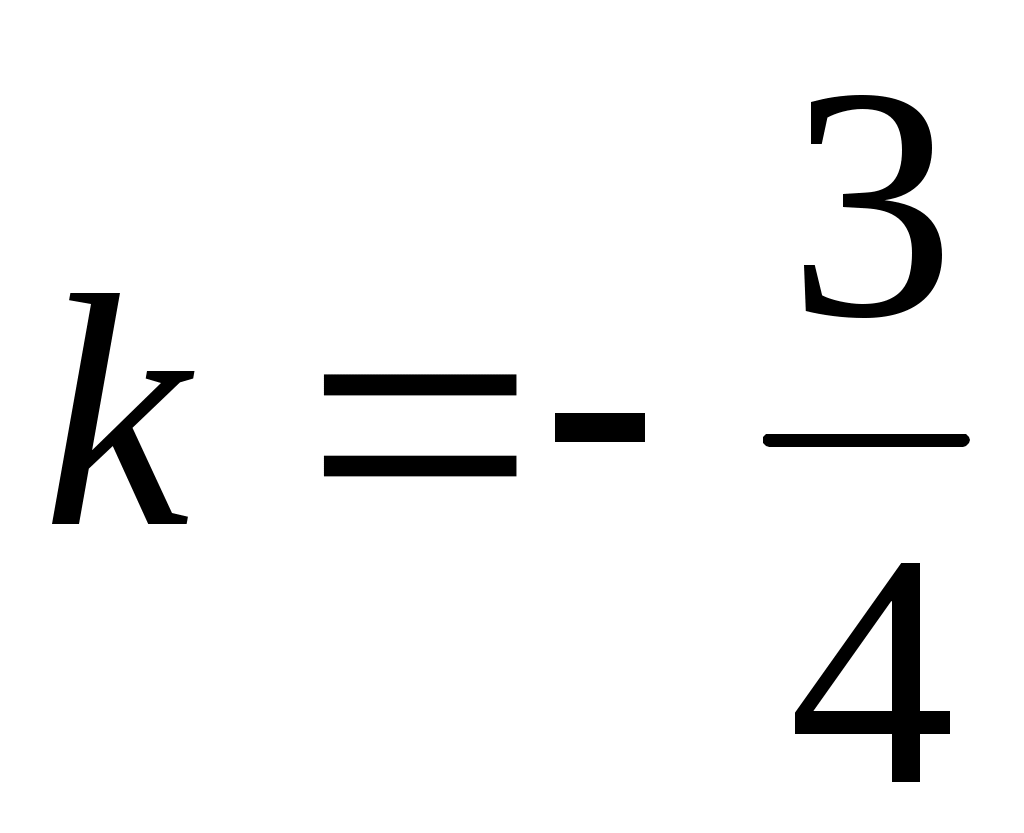 . По условию, искомая прямая проходит через точку . По условию, искомая прямая проходит через точку 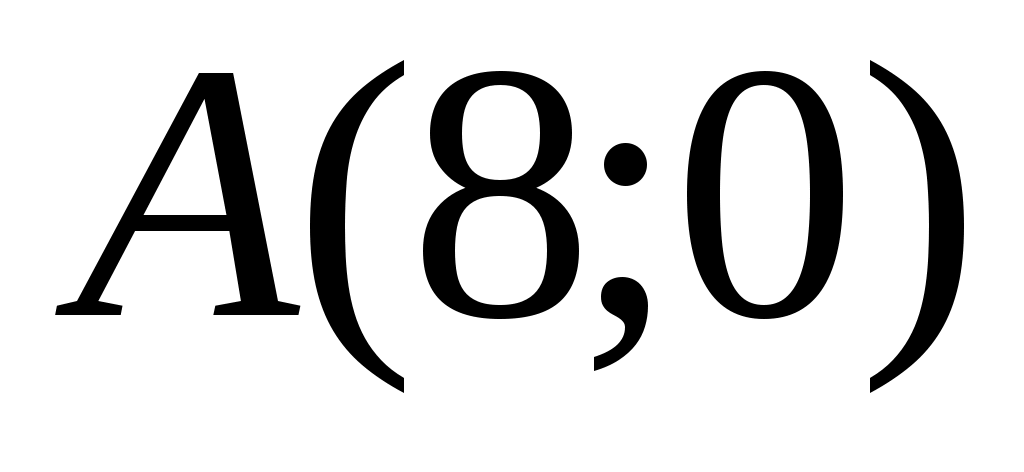 , значит, ее уравнение будет иметь вид: , значит, ее уравнение будет иметь вид:
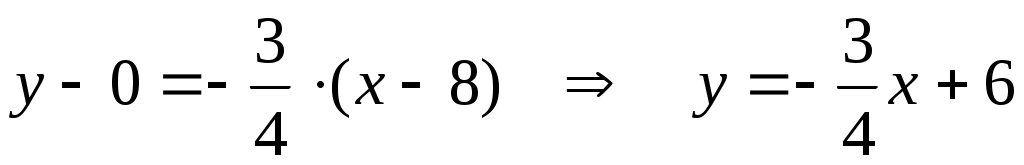
д) Косинус угла между двумя прямыми 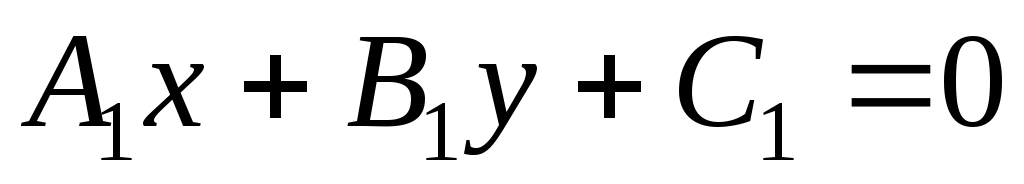 и и 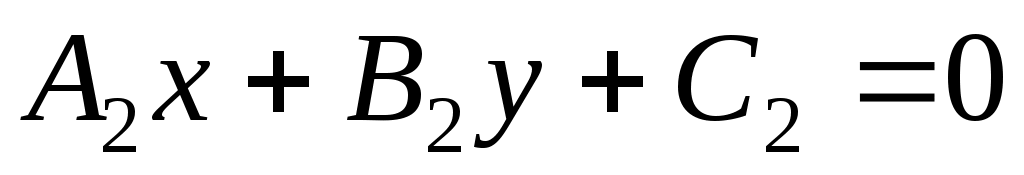 найдем по формуле найдем по формуле
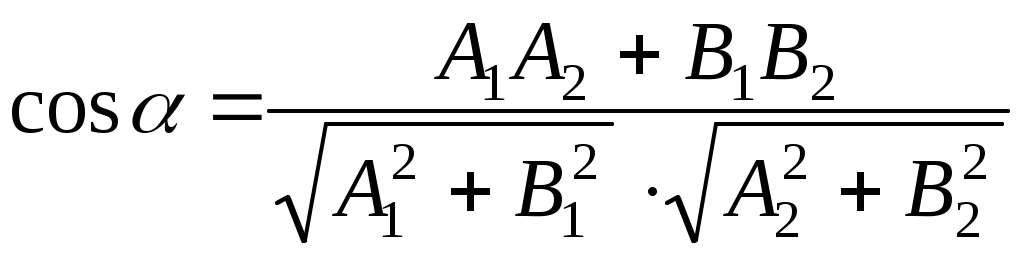
Запишем общие уравнения прямых  и и  : :
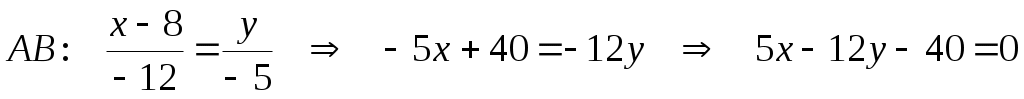 ; ;
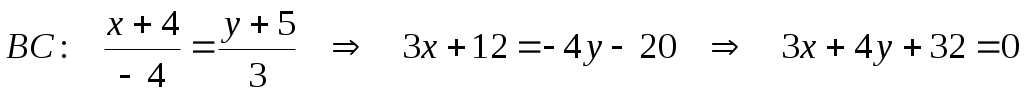 . .
Тогда по формуле косинуса угла между прямыми, находим:
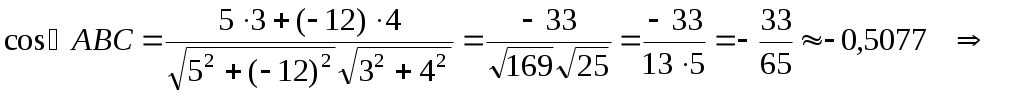
По таблицам Брадиса находим: 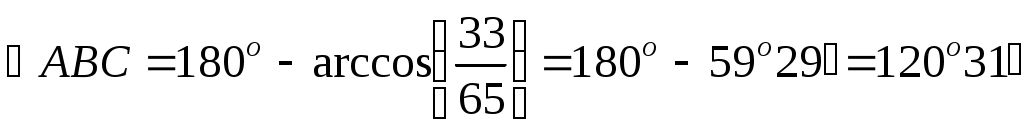
2.1.5. Найти пределы
а) 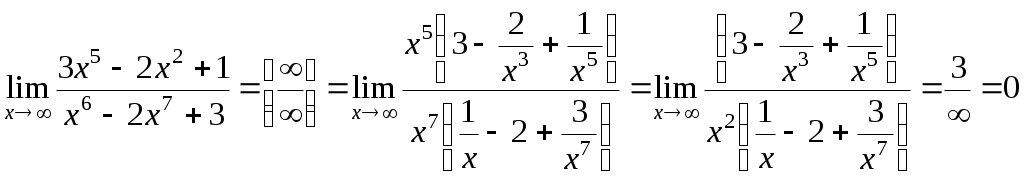
б) 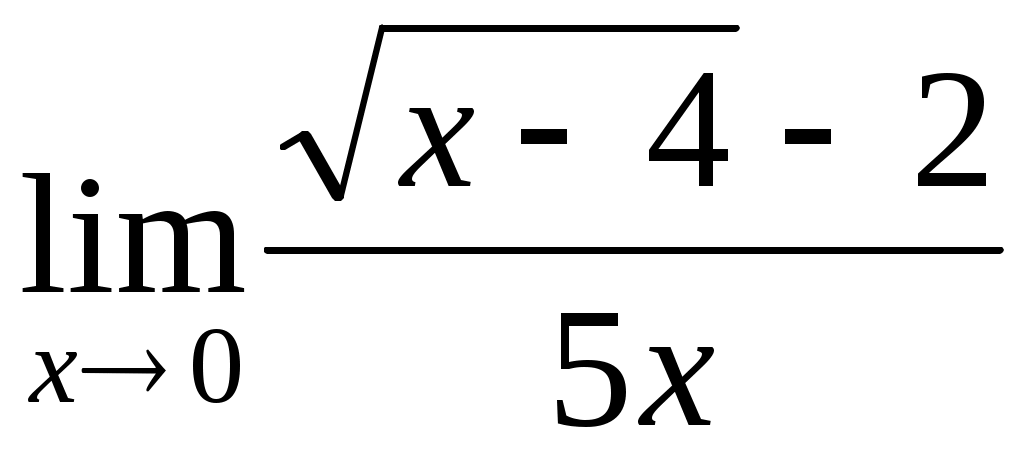 предел не существует, так как предел не существует, так как 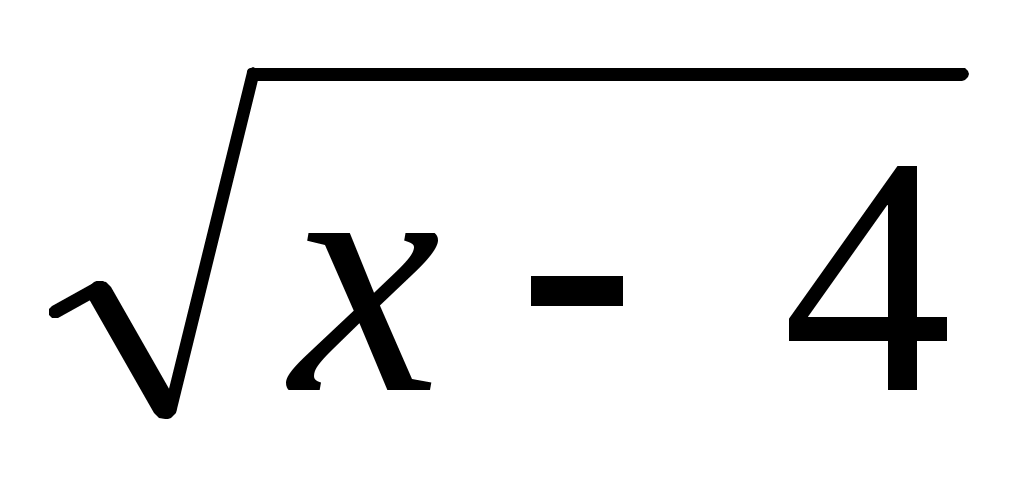 не существует при не существует при 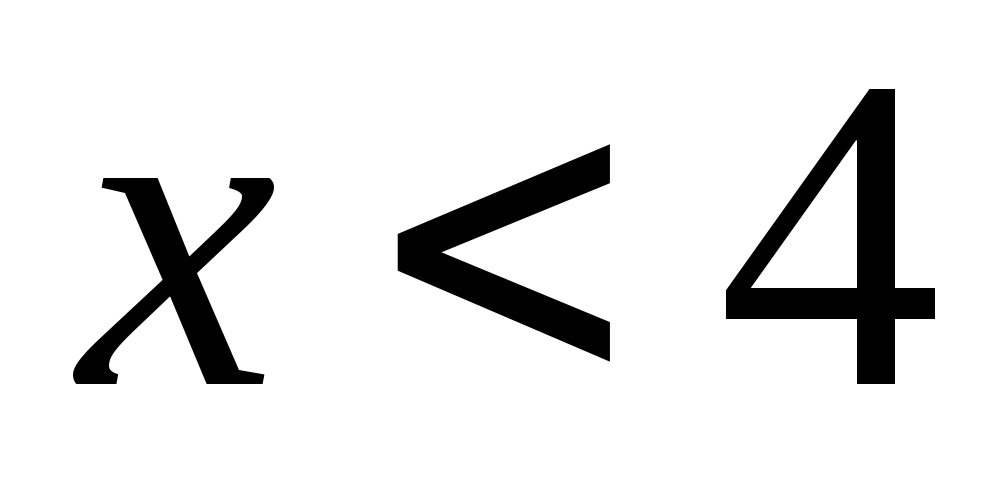 . .
Наверное в условии ошибка и должно быть так:
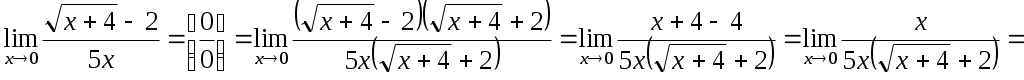
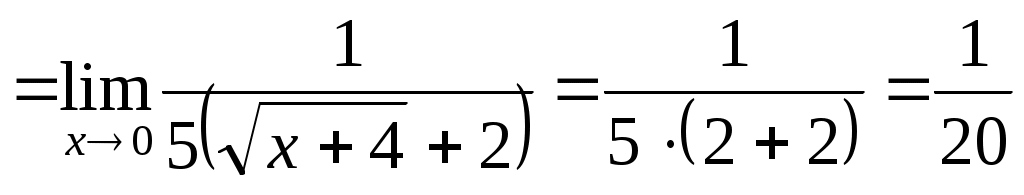
в) 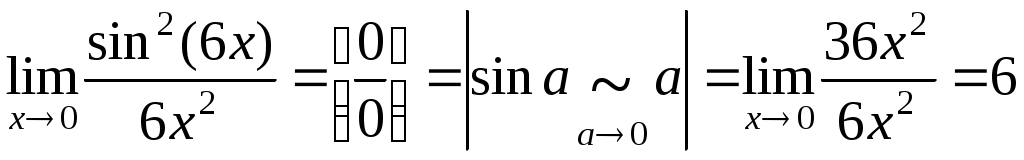
г) 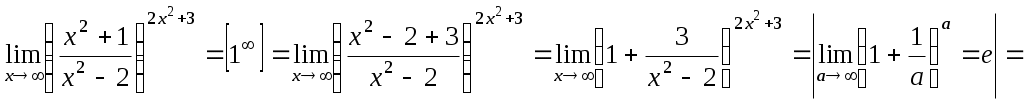
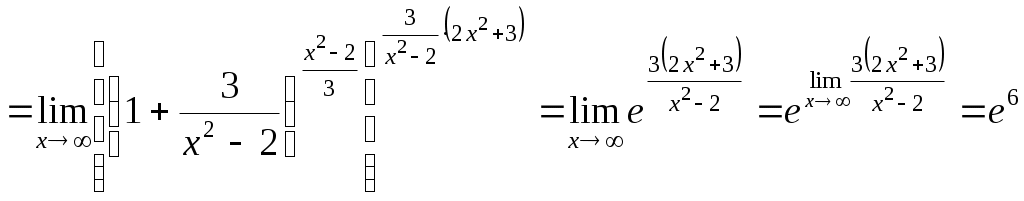
2.2.5. Найти производную 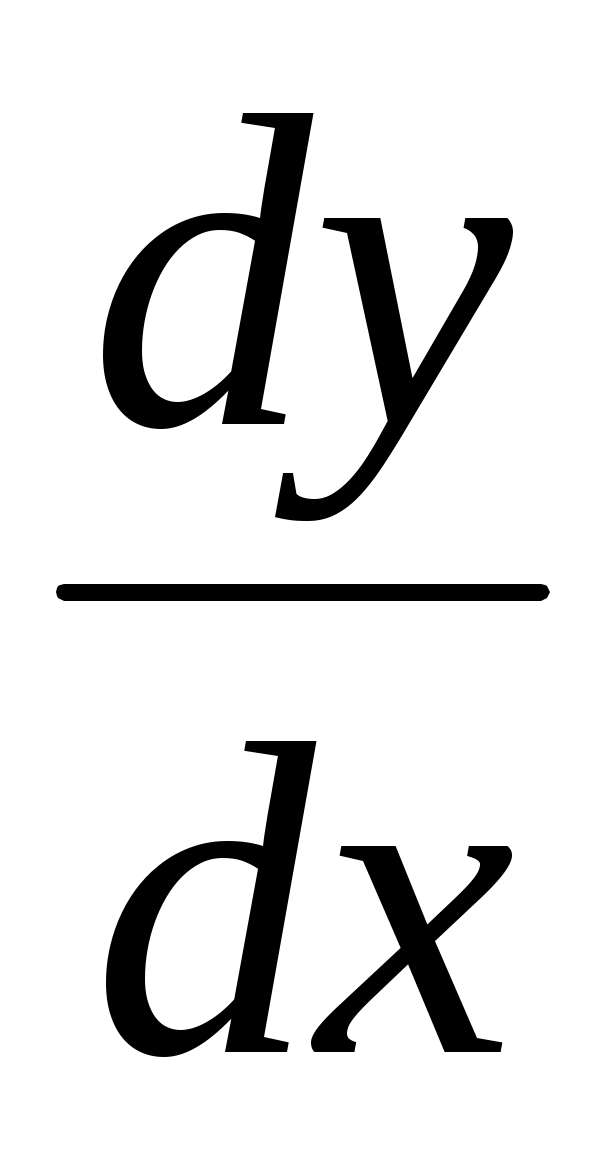 : :
а) 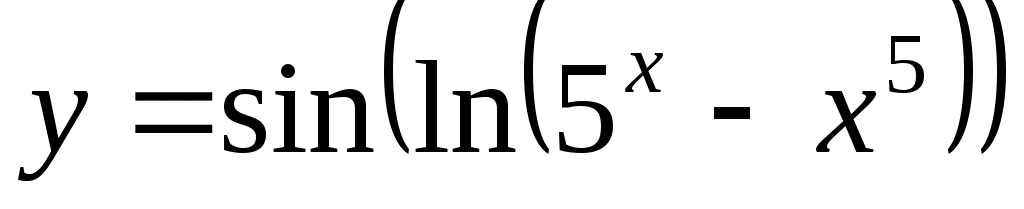
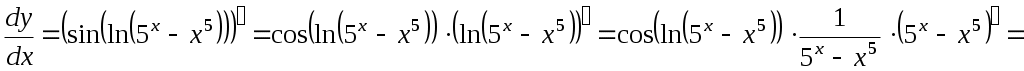
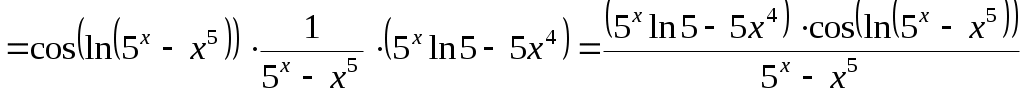
б) 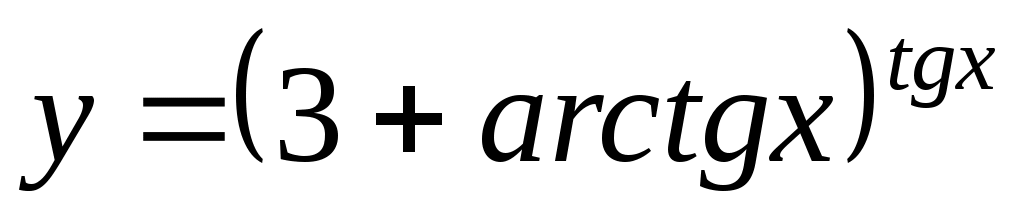
Прологарифмируем обе части данного равенства:

Учитывая, что  является функцией от является функцией от 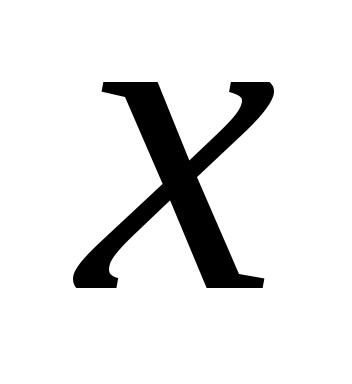 , найдем производные обеих частей равенства по , найдем производные обеих частей равенства по 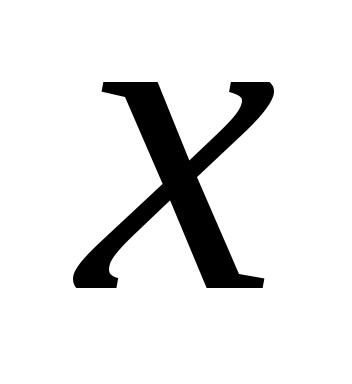 : :
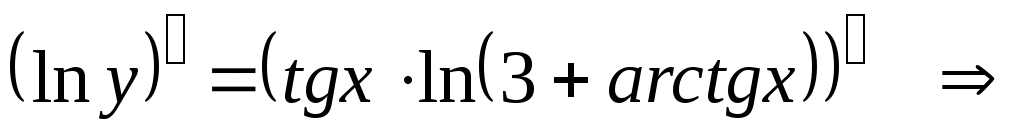
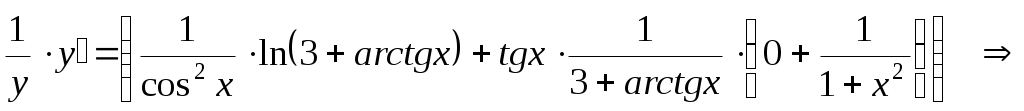
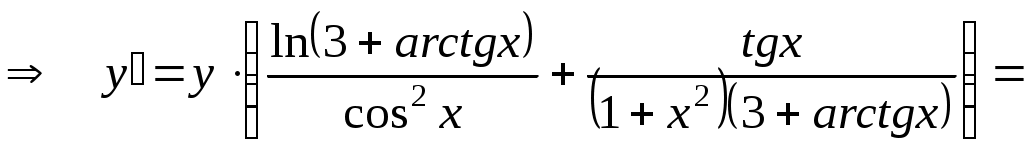
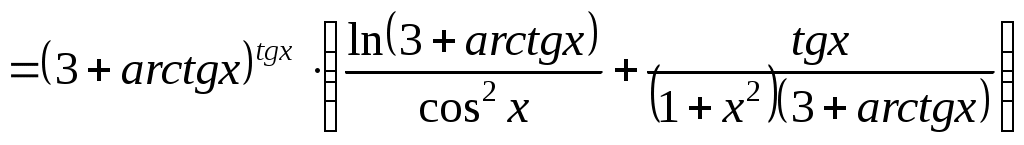
в) 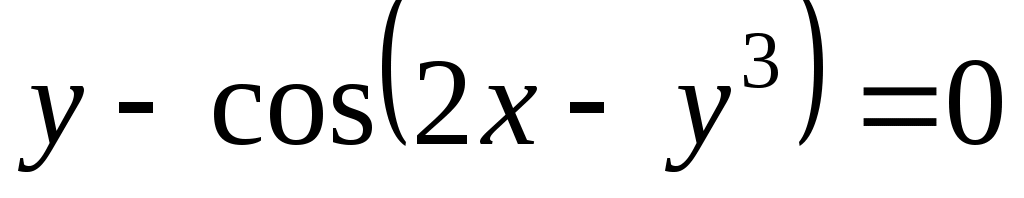
Дифференцируем обе части равенства по 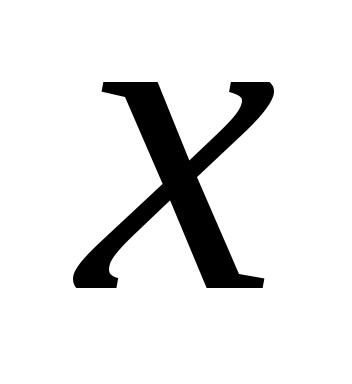 , считая , считая 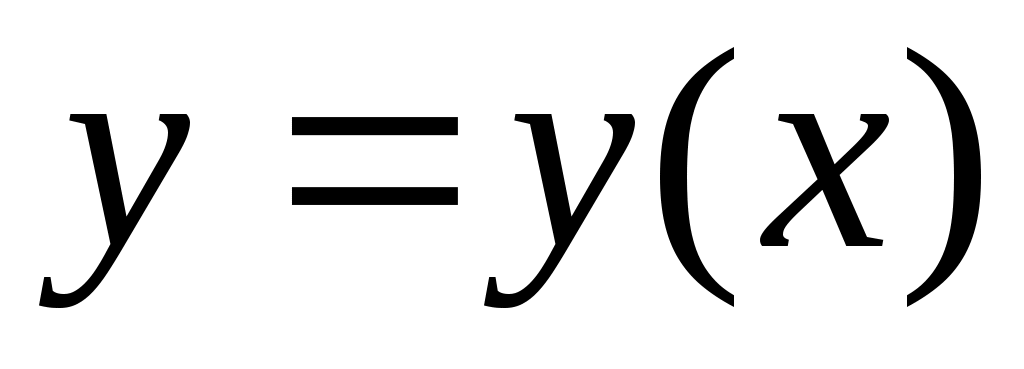 функцией от функцией от 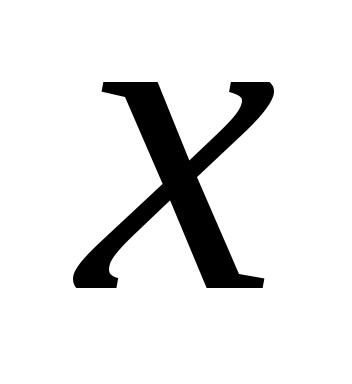 : :
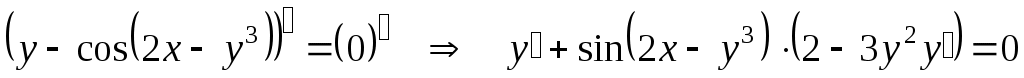
Теперь из полученного выражения выразим  : :
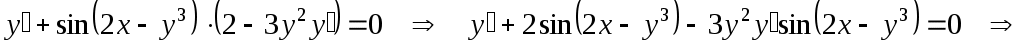
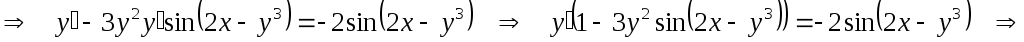 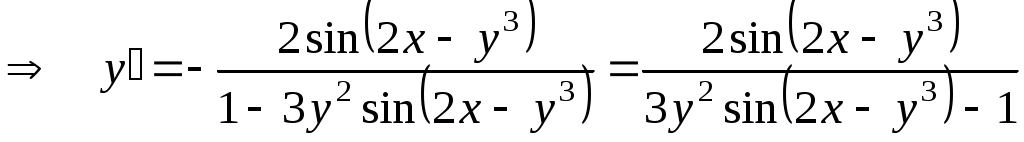
г) 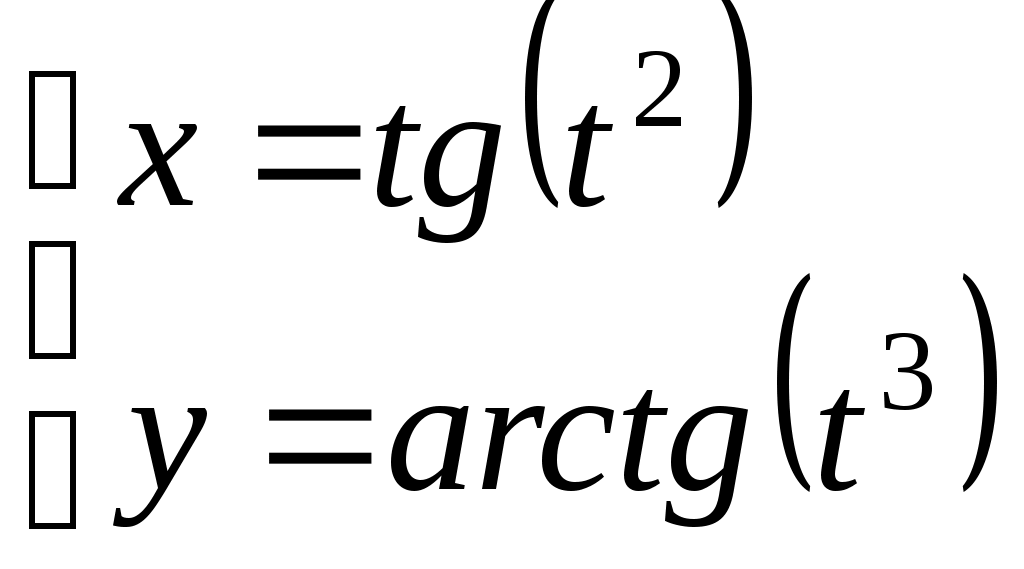
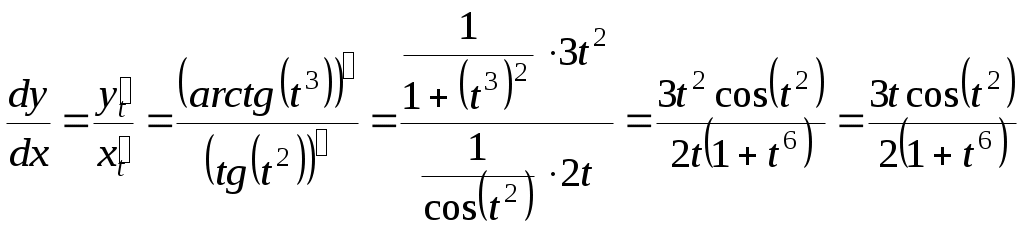
|
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.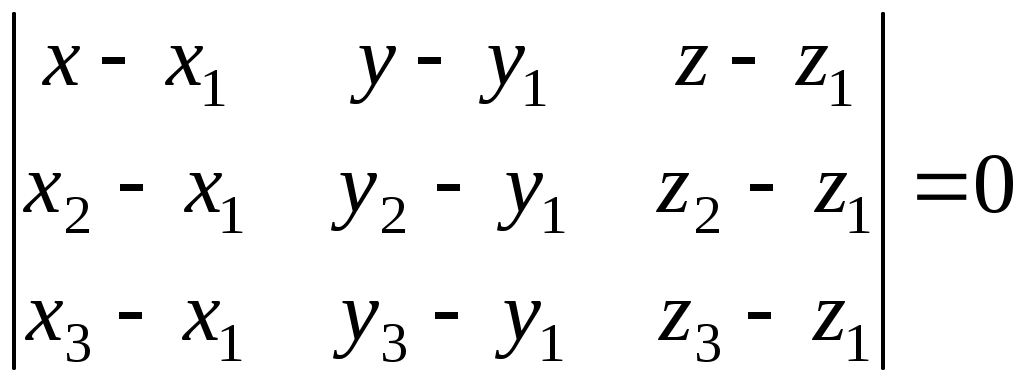 .
.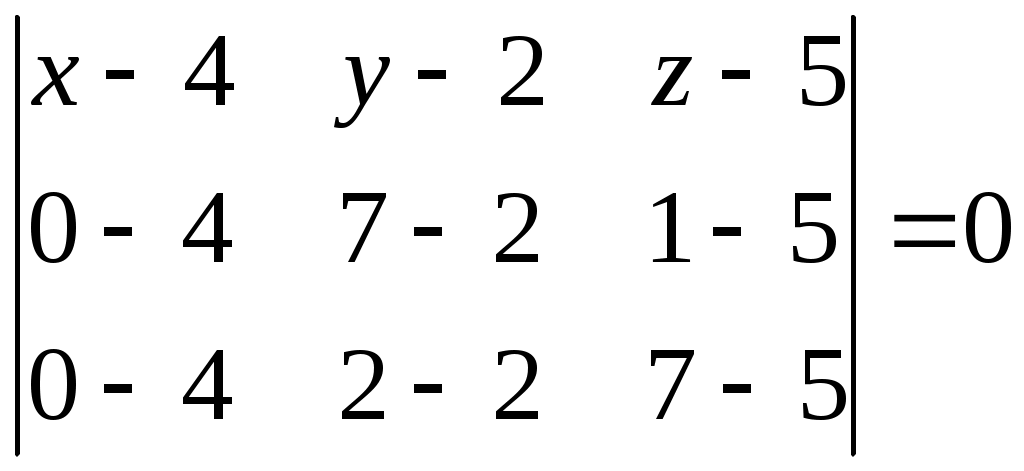 ;
; 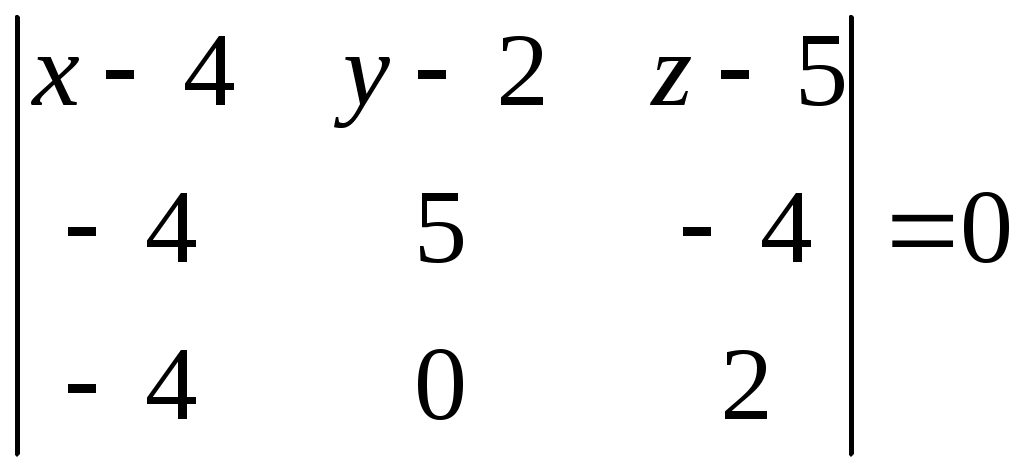 ;
;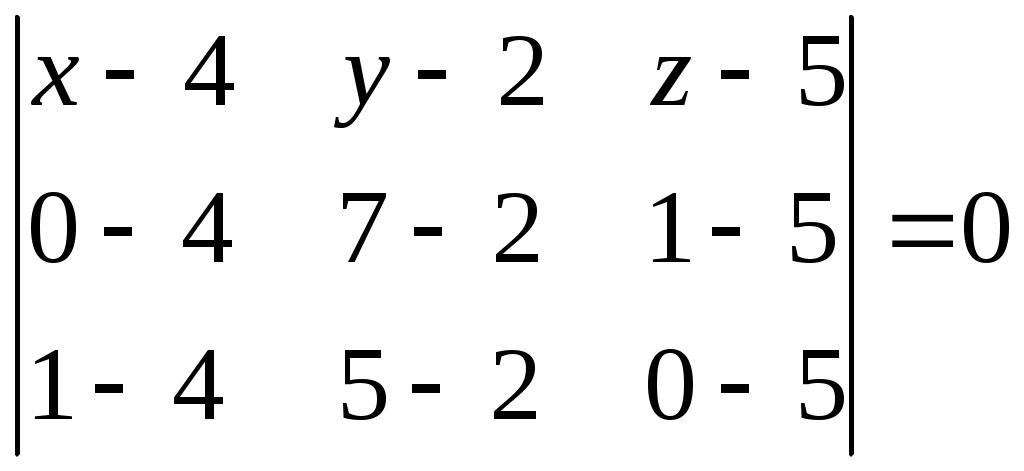 ;
; 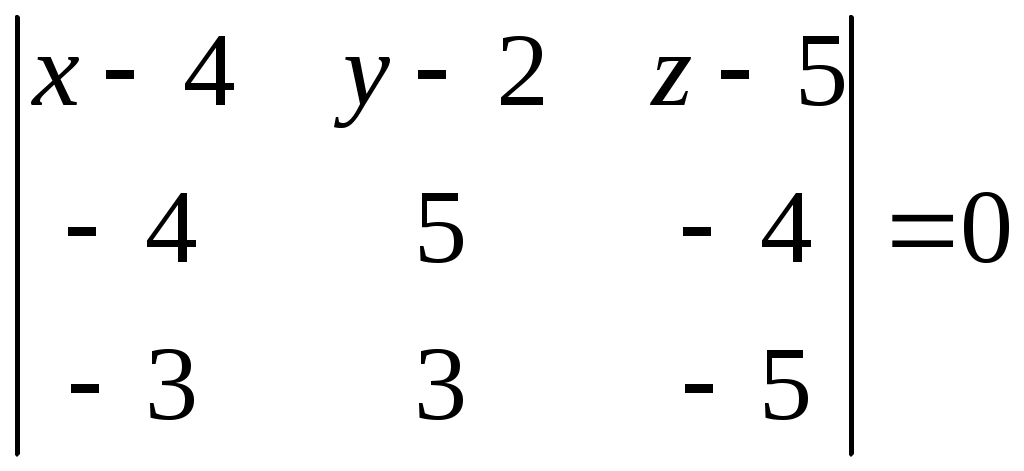 ;
;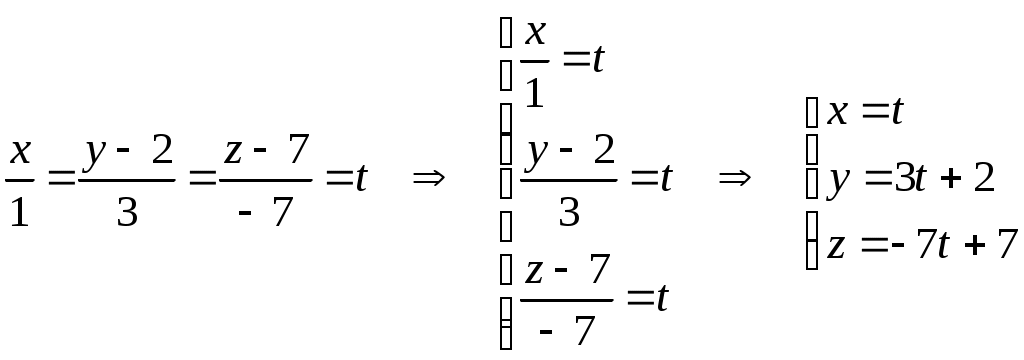 .
.