Контрольная работа_Павлов.М.Д. Контрольная работа 1 Задача Заданы матрицы А, В, С. Найти а б вычислить определитель матрицы А
 Скачать 1.04 Mb.
|
|
2.3.5. Найти наибольшее и наименьшее значения функции  на отрезке   ,  Функция достигает наибольшего и наименьшего значения либо в стационарных точках, принадлежащих заданному отрезку, либо на концах этого отрезка. Найдем стационарные точки. Для этого найдем  и выясним, где  и где  не существует: ; ; не существует при  .Следовательно достаточно вычислить значения функции на концах отрезка и выбрать из них наибольшее и наименьшее значения:  ;  Таким образом:  наибольшее значение функции;  наименьшее значение функции.Задача 2.4.5. Провести полное исследование функции и построить график функции  1) Данная функция не определена в точке  , так как в этой точке знаменатель дроби обращается в ноль. Значит, область определения функции:  .2) Выясним характер разрыва функции при . Для этого вычислим односторонние пределы функции в точке : ;  Следовательно, точка является точкой разрыва 2-го рода для данной функции, а прямая – вертикальной асимптотой графика функции.3) Проверим наличие наклонных асимптот вида 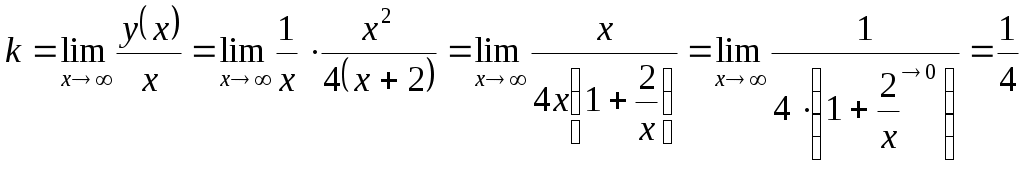 . Вычислим коэффициенты  и  :  Следовательно,  – уравнение наклонной асимптоты.4) Свойство четности.  функция общего вида. 5) Точки пересечения с осями координат. С осью  :  – точка  .С осью  :  – точка  .6) Интервалы возрастания и убывания функции, точки экстремума. Найдем производную заданной функции:  Найдем критические точки из условий  и  не существует: ;  не существует при .Нанесем найденные критические точки на числовую ось и исследуем знак производной слева и справа от каждой из них: 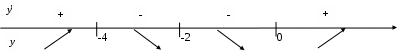 Поскольку при  производная  , то на этих интервалах функция возрастает; на интервалах  производная  , значит, на этих интервалах функция убывает. Так как при переходе через точку  производная сменила свой знак с «-» на «+», значит, в этой точке функция достигает минимум, причем  . При переходе через точку  производная сменила свой знак с «+» на «-», значит, в этой точке функция достигает максимум, причем  .7) Интервалы выпуклости и вогнутости, точки перегиба. Вторая производная функции имеет вид:   Критические точки находим из условий  и  не существует:  ;  не существует при .Построим числовую прямую, отложим критические точки и, подставляя во вторую производную точки из интервалов, вычислим знаки: 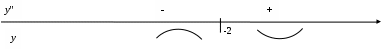 Следовательно, график функции является выпуклым при  и вогнутым на интервале  . 8) Сведем результаты проведенного исследования в таблицу:
9) Используя результаты исследования функции, строим график 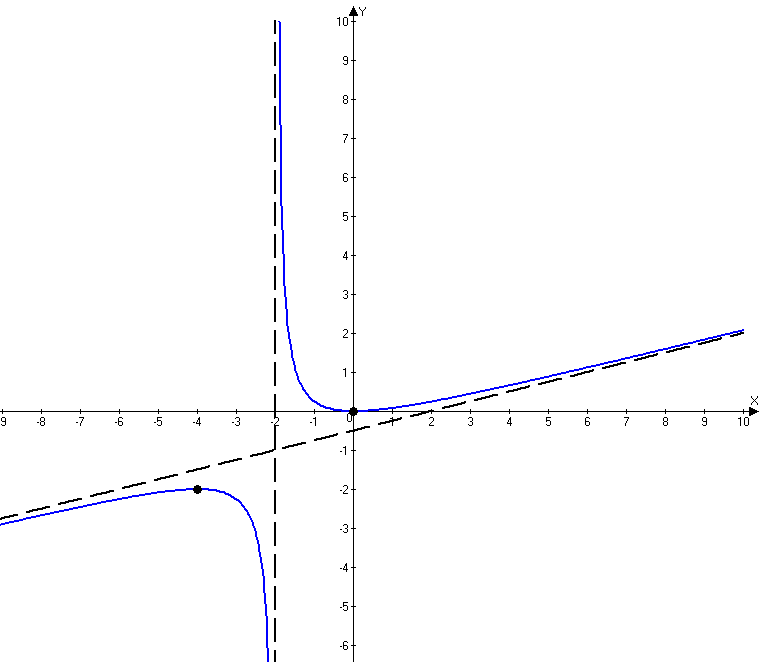 Контрольная работа № 3 Задача 2.5. Найти и построить область определения функции двух переменных 5.  Данная функция определена при  , т.е. .Таким образом, областью определения данной функции является часть плоскости, расположенная между прямыми: 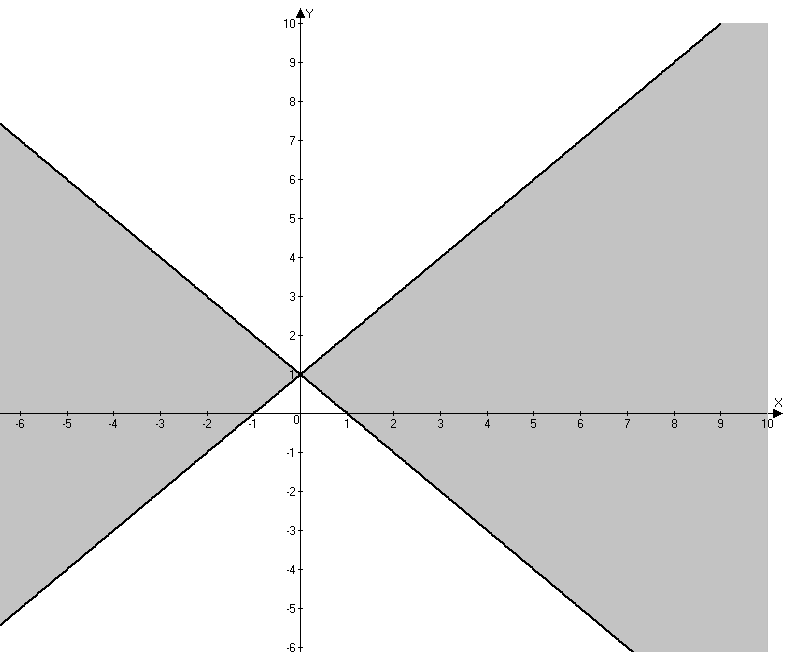 2.6.5. Найти частные производные первого порядка  При нахождении частной производной по  переменную  считаем постоянной, а при нахождении частной производной по переменную считаем постоянной: ; .2.7.5. Найти точки локального экстремума функции  Запишем необходимые условия экстремума, найдем стационарные точки 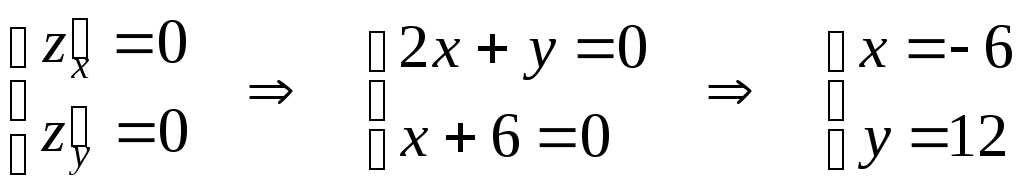 Таким образом, получили одну стационарную точку  .Проверим выполнение достаточного условия экстремума для найденной стационарной точки. Для этого найдем частные производные второго порядка:  .Поскольку частные производные второго порядка равны константам, то они и будут равны соответствующим константам и в точке : .Вычислим  .Поскольку  , то в точке экстремума нет.2.8. Найти  и  , если известны: функция  , точка  и направление  5.  ,  ,  Градиент функции  в точке найдем по формуле: Найдем частные производные  и вычислим их значения в точке : ; .Следовательно:  .Производную функции в точке по направлению вектора  найдем по формуле ,где  – направляющие косинусы данного направления.Значение частных производных в точке найдено. Найдем направляющие косинусы данного направления:  ,  .Тогда  .2.9.5. Найти неопределенные интегралы а) 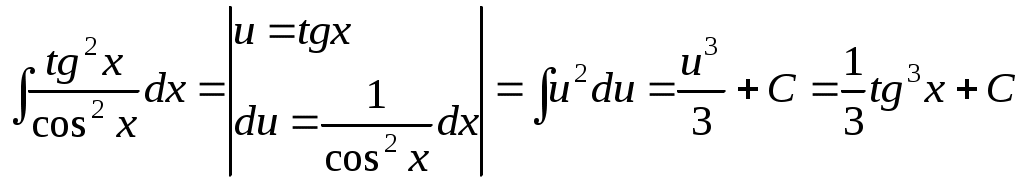 б) 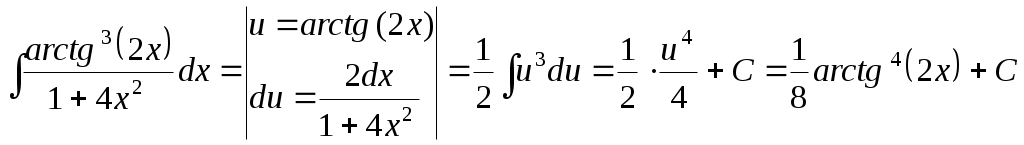 в)  |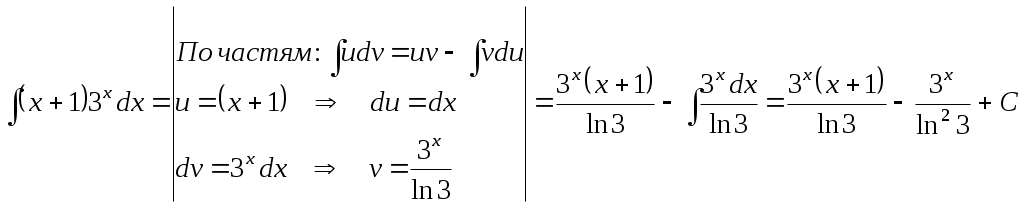
