Контрольная работа_Павлов.М.Д. Контрольная работа 1 Задача Заданы матрицы А, В, С. Найти а б вычислить определитель матрицы А
 Скачать 1.04 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «СибирскИЙ государственнЫЙ Университет геоСИСТЕМ И ТЕХНОЛОГИЙ» (СГУГИТ)  Контрольные работы по математике Вариант №5 Выполнил обучающийся группы 1И-у Павлов М.Д Проверил Логачёв Артем Васильевич Новосибирск – 2020 Контрольная работа № 1 Задача 1.1. Заданы матрицы А, В, С. Найти: а)  ; б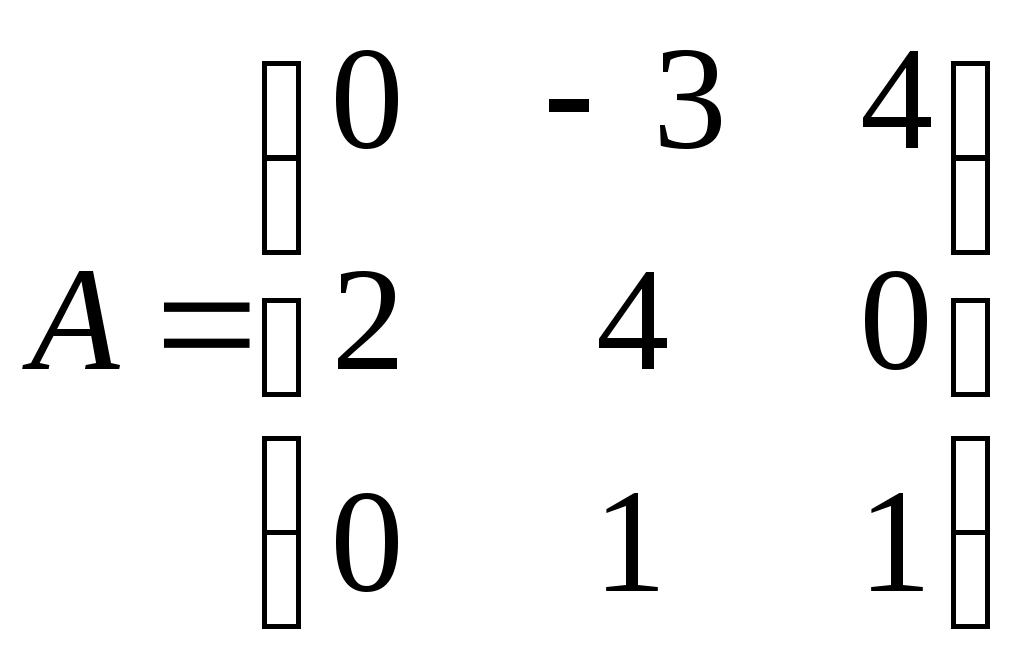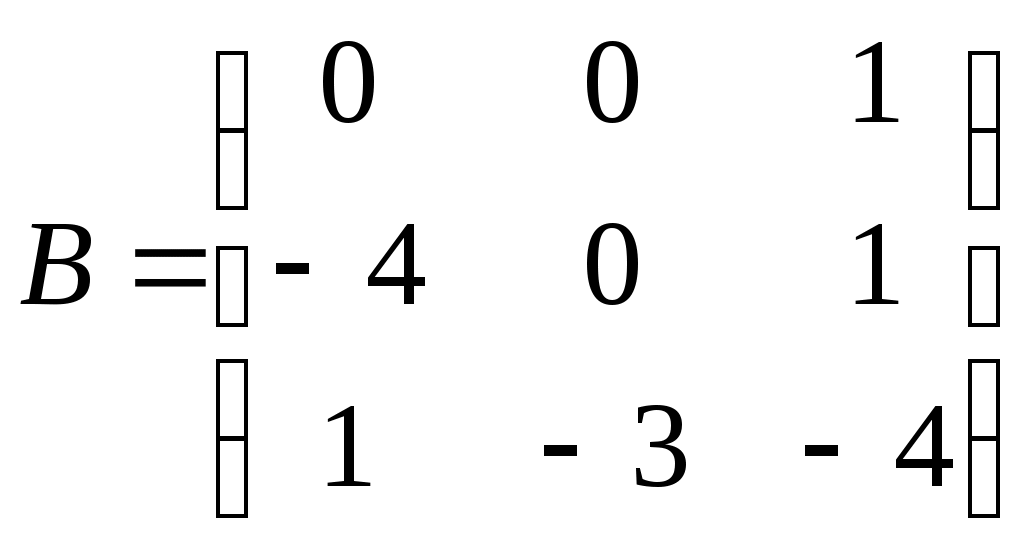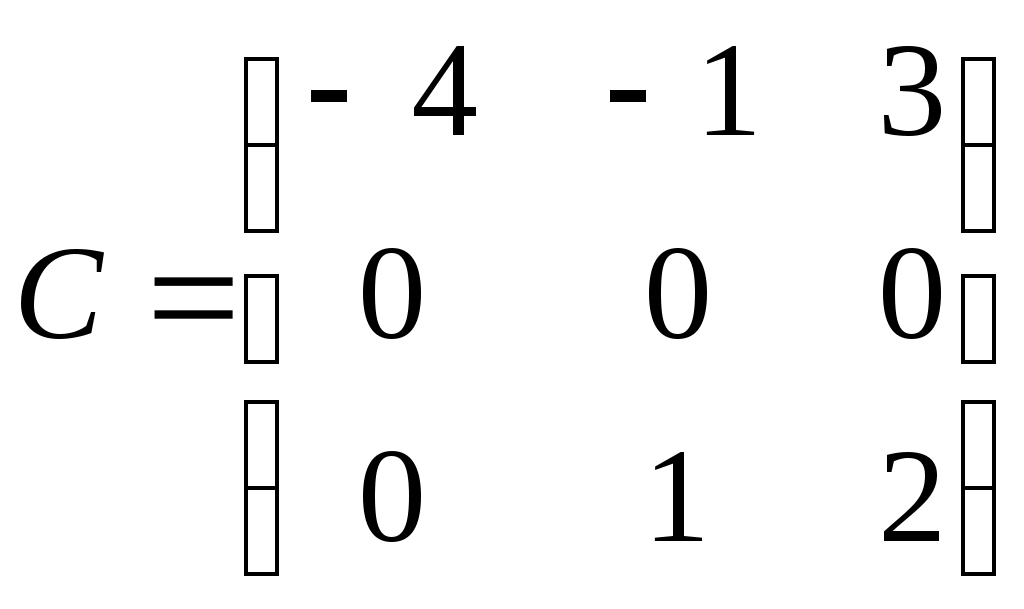) вычислить определитель матрицы А5.  ,  ,  а) Вычислим по действиям: 1) 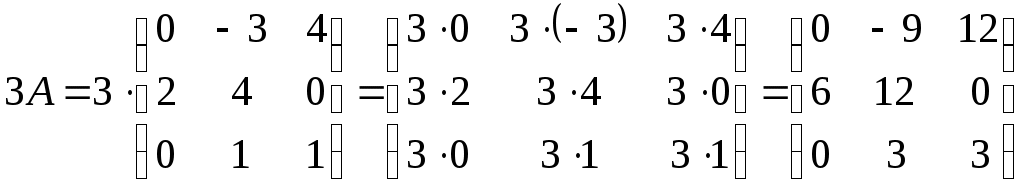 2) 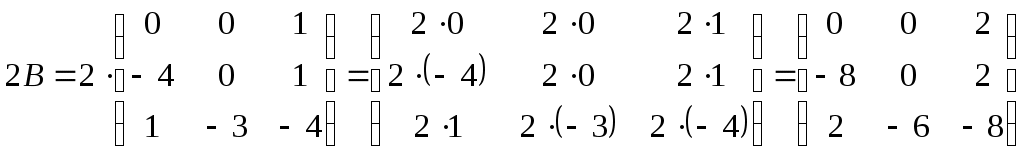 3) 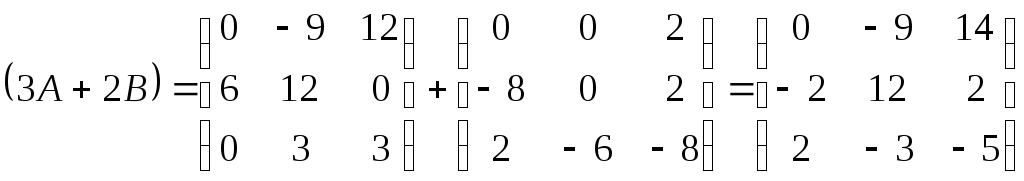 4) 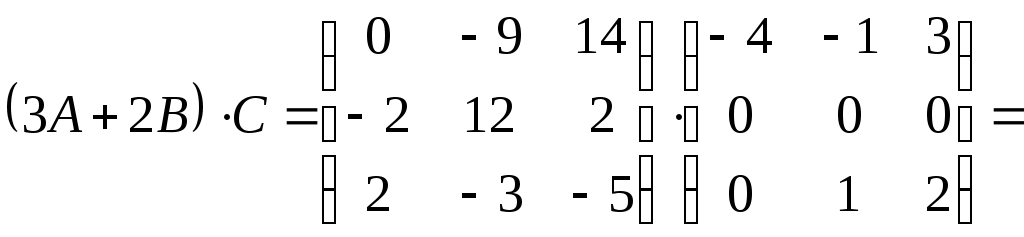 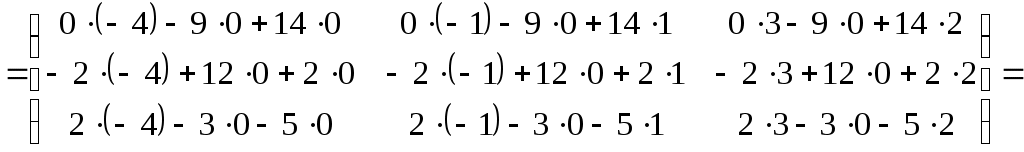 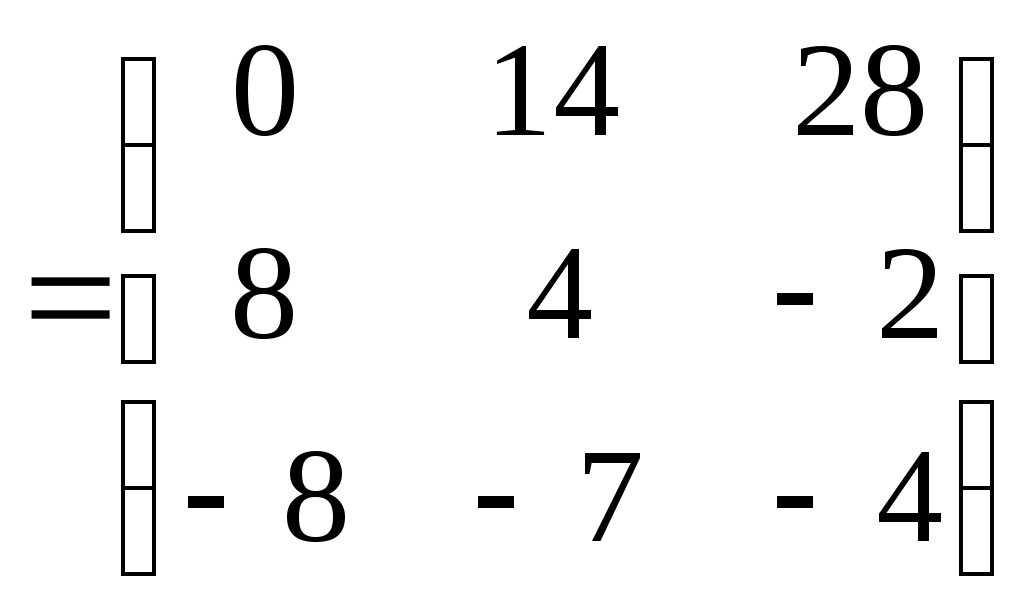 Таким образом: 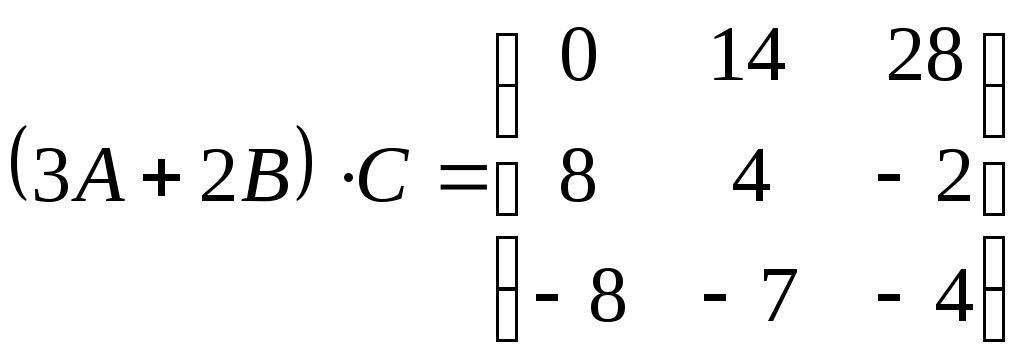 б) 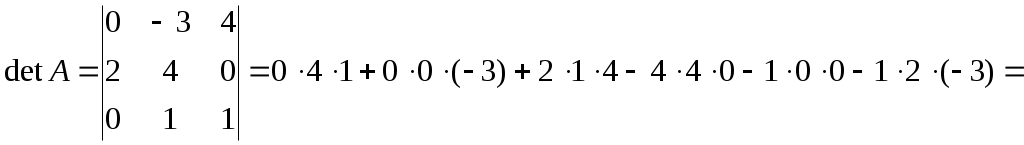  Задача 1.2. Для матрицы  н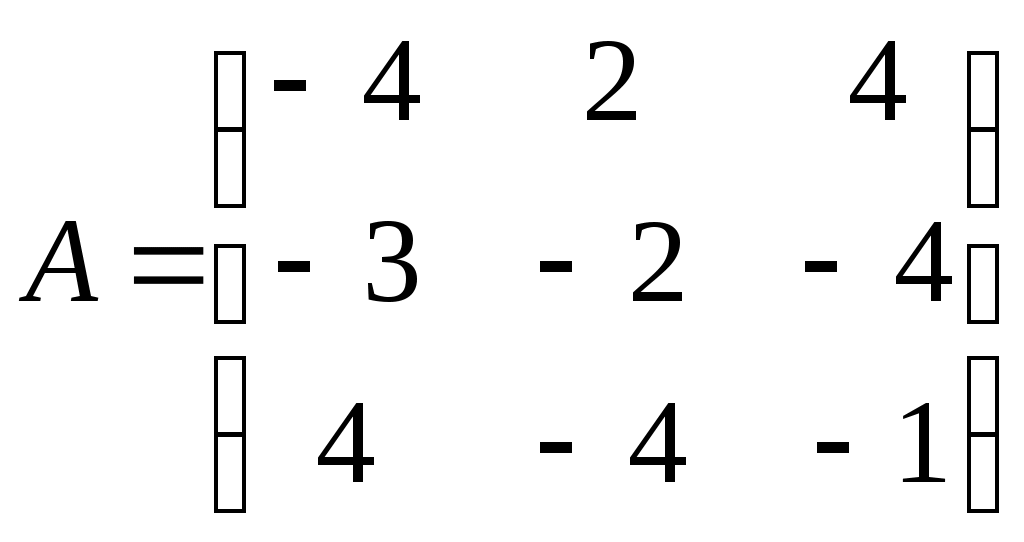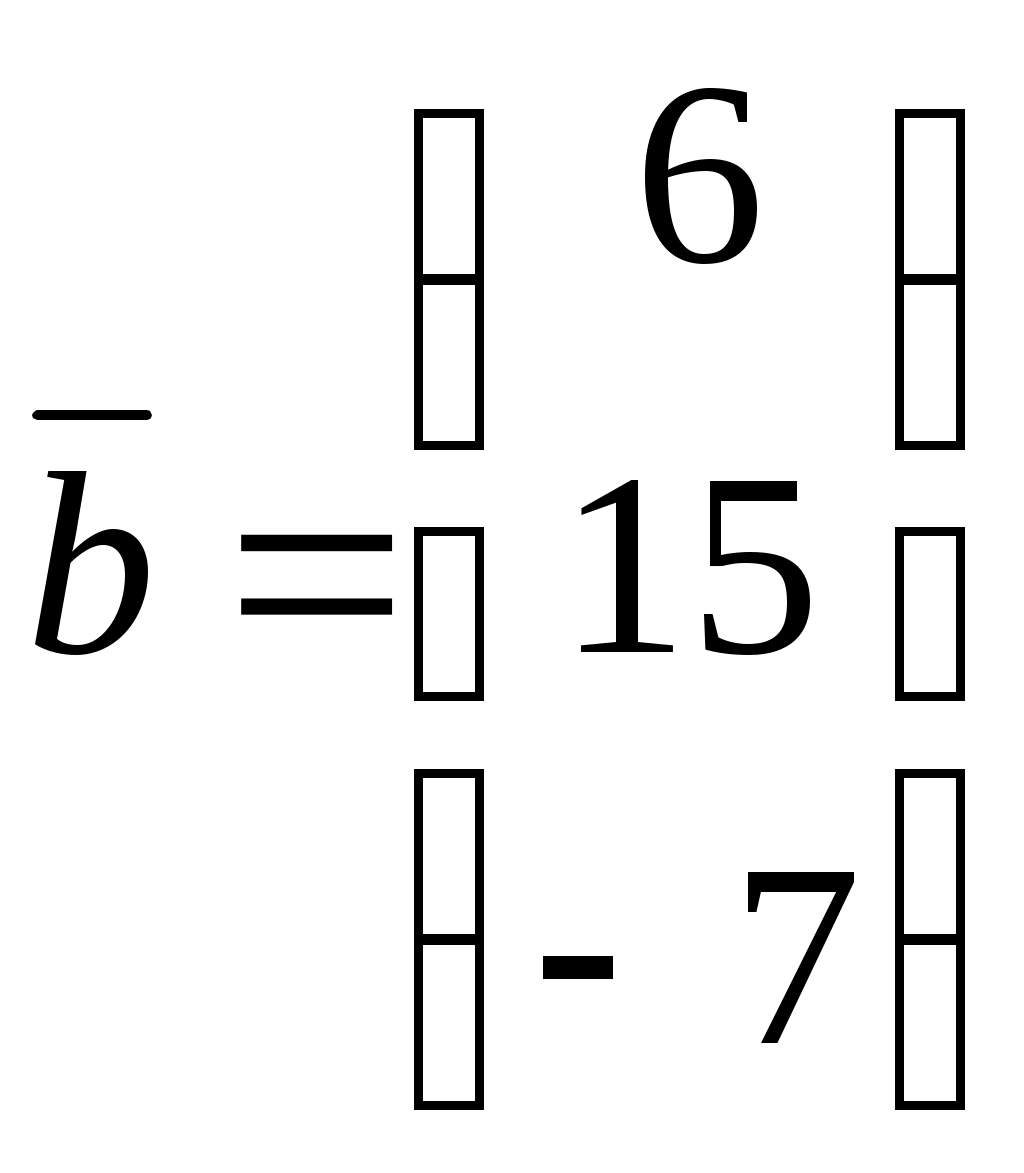айти: а)  ; б)  ; в) решить систему  матричным методом5.  ,  а) Вычислим определитель матрицы 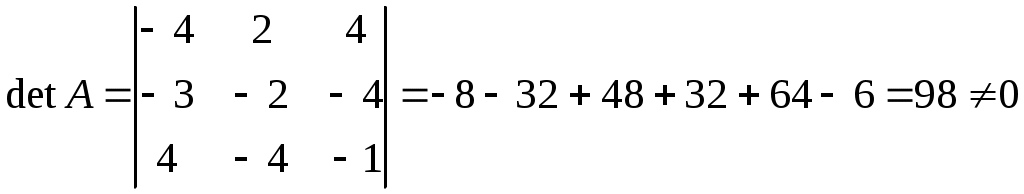: Поскольку определитель матрицы не равен 0, то матрица является невырожденной и обратная матрица существует..Найдем алгебраические дополнения для каждого элемента матрицы  ;  ;  ; ;  ;  ; ;  ;  .Тогда обратная матрица: 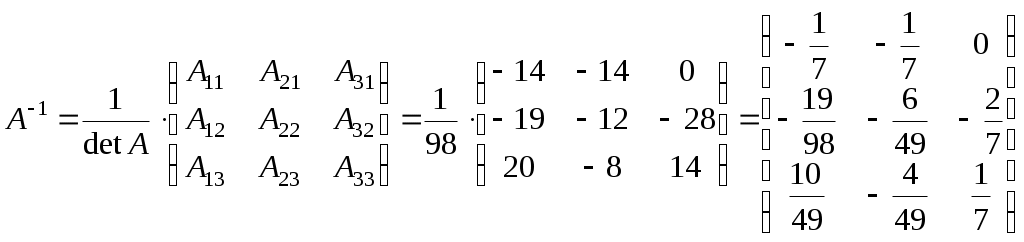 .б) 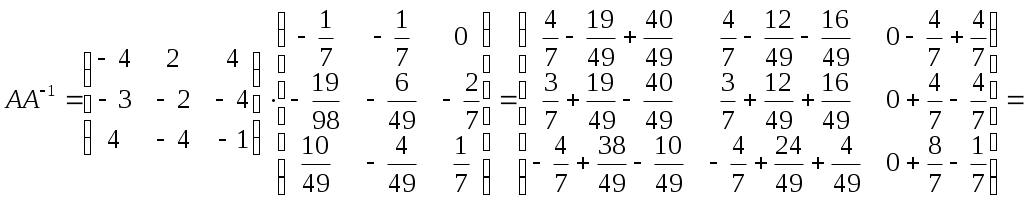 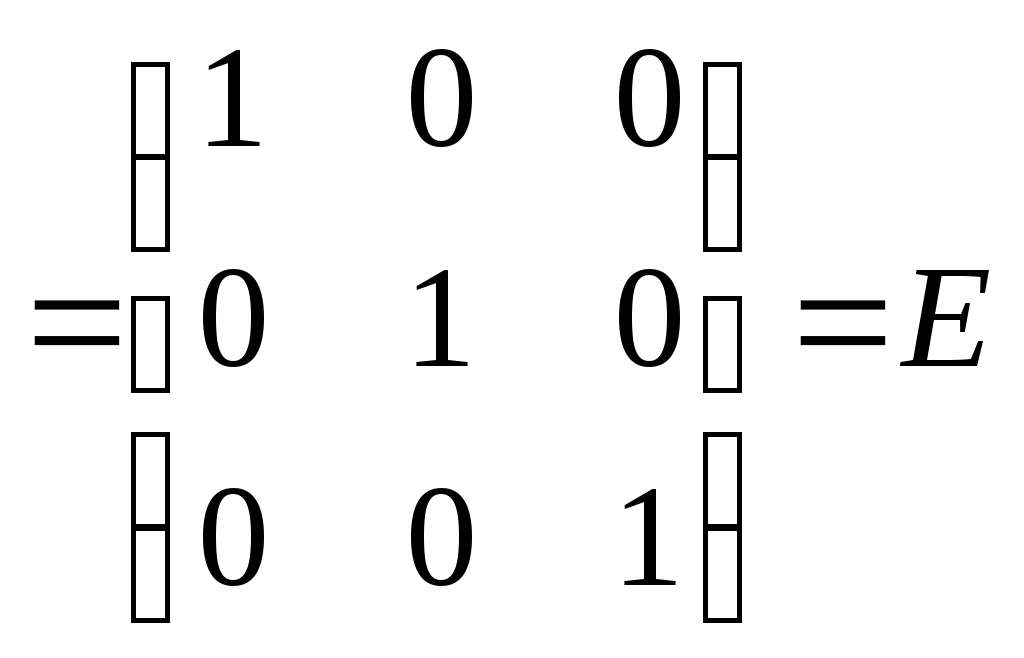 в) Разрешаем матричное уравнение относительно  : ;  ;  .По последней формуле будем находить решение системы. Обратная матрица имеет вид: 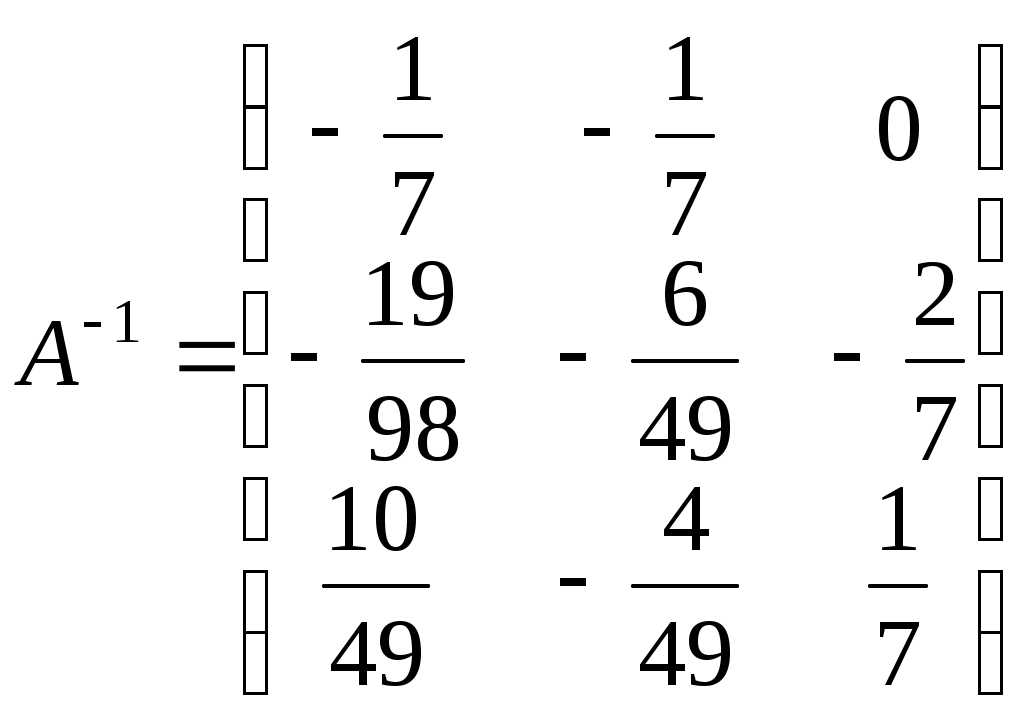 Тогда 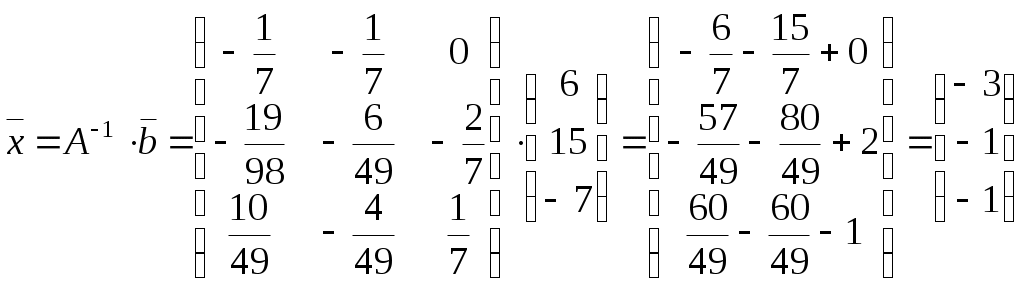 .Задача 1.3. Решить систему уравнений методом Гаусса 5. 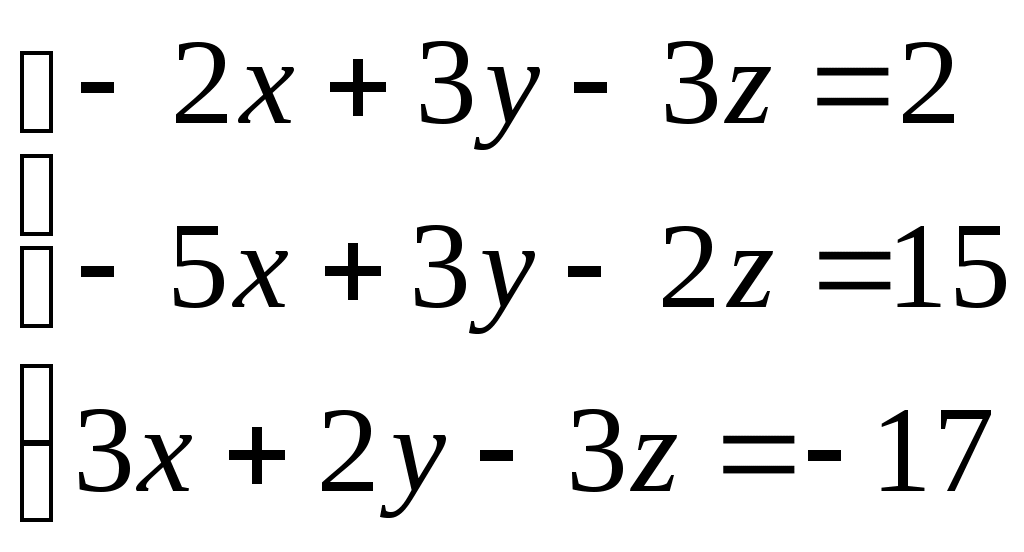 Составим расширенную матрицу системы и приведем ее к ступенчатому виду: 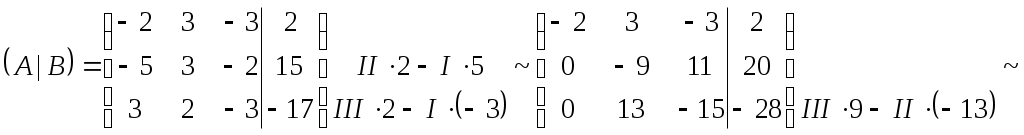 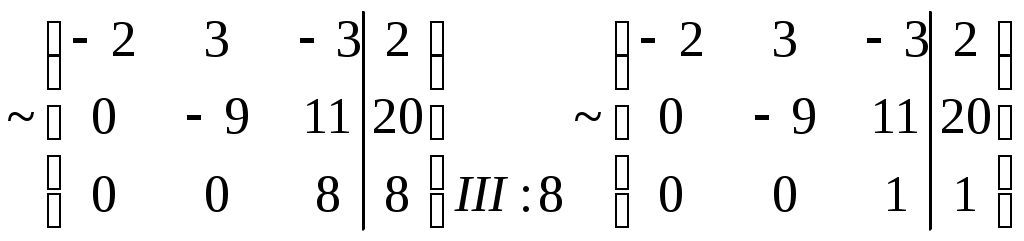 Из последней полученной расширенной матрицы запишем уравнения, и применяя обратный ход Гаусса найдем неизвестные: 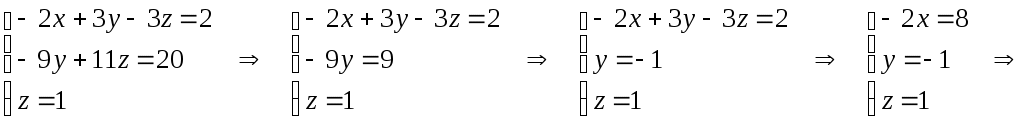 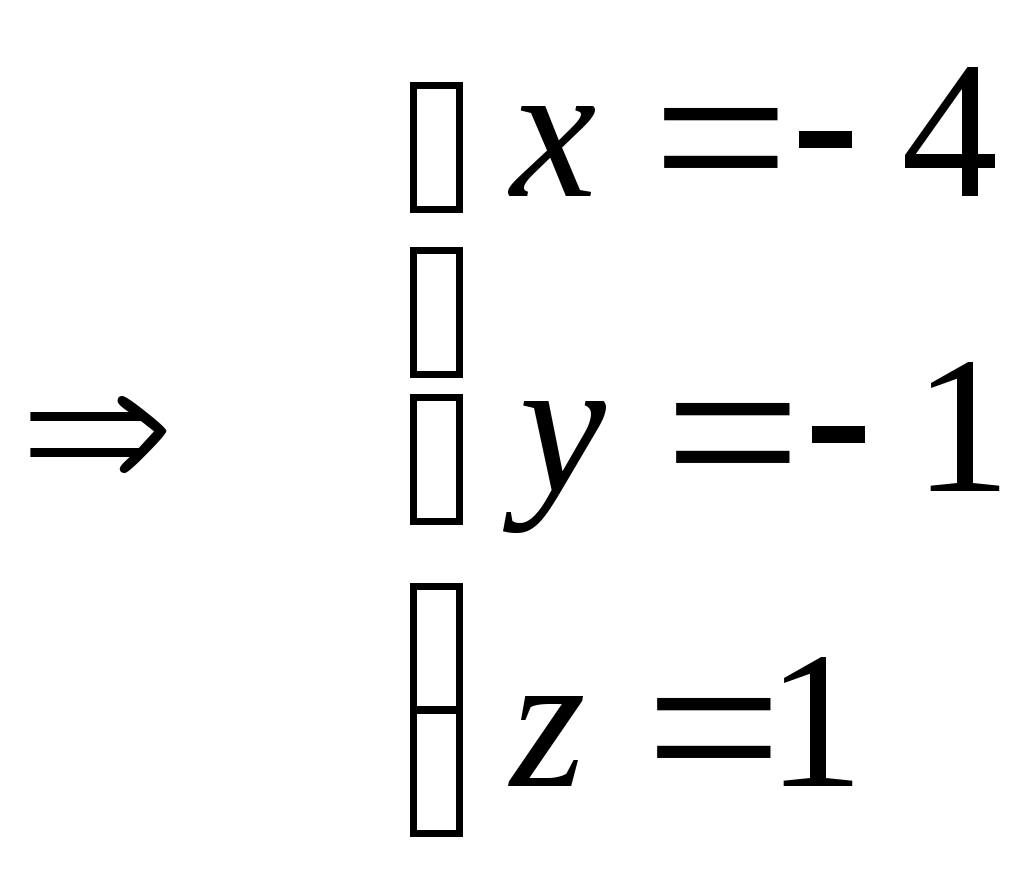 Задача 1.4.5. Исследовать совместность каждой системы а) и б), для совместной системы найти решение а) 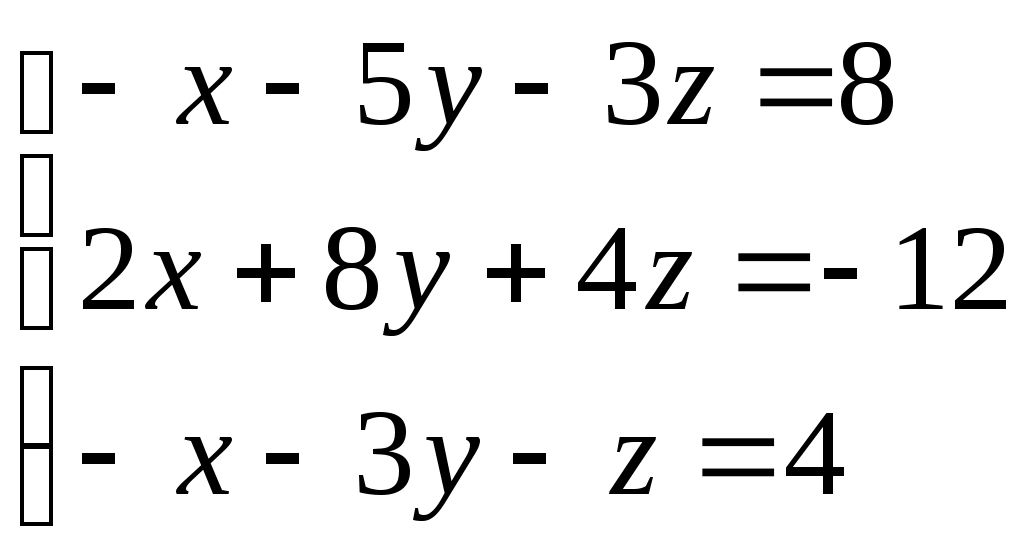 Составим расширенную матрицу системы и приведем ее к ступенчатому виду: 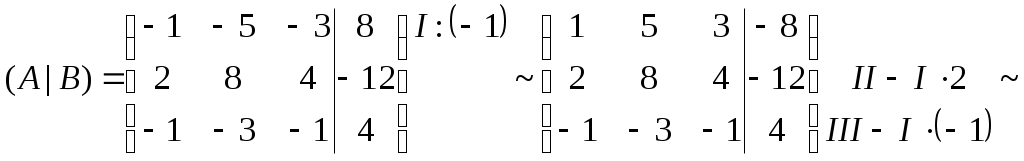 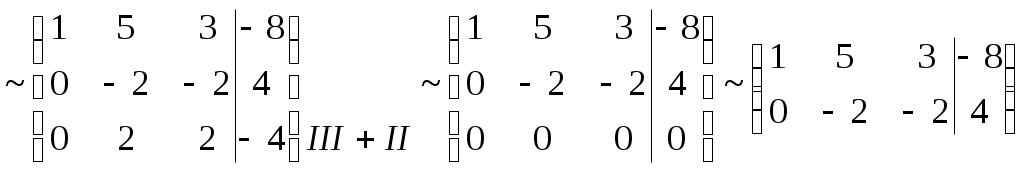 Минор  имеет наивысший порядок, равен 2. Он принадлежит как основной матрице системы, так и расширенной. Следовательно,  . Значит, согласно теореме Кронекера-Капелли, система совместна. Поскольку  (где  количество неизвестных), то система имеет бесконечное число решений.Указанный минор является базисным. В него вошли коэффициенты при неизвестных  , значит, неизвестные - зависимые (базисные), а  - свободные.Из последней матрицы выпишем систему, эквивалентную исходной и методом исключения неизвестных найдем выражения зависимых переменных через свободные: 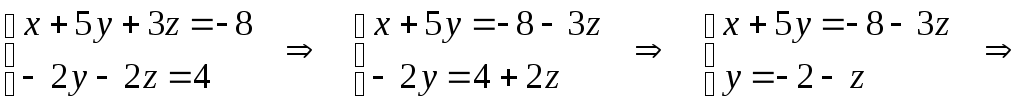 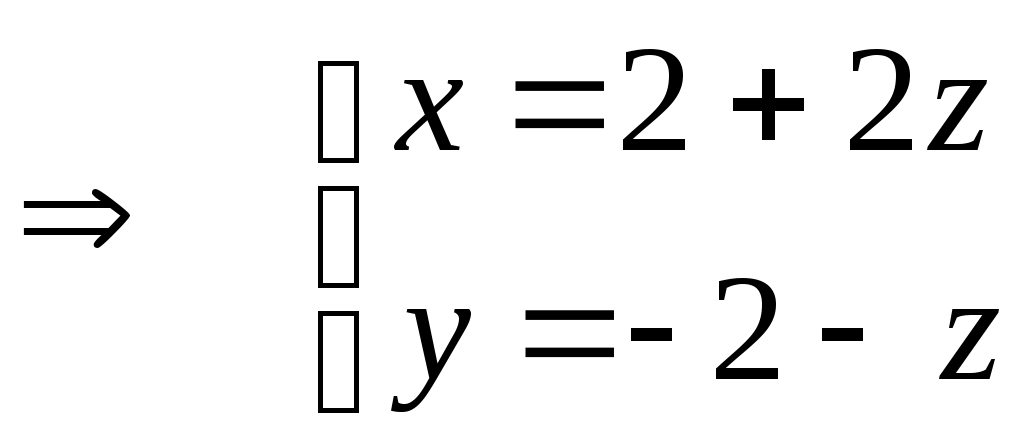 Таким образом, получили общее решение системы. Придавая свободным неизвестным любые значения, получим сколь угодно частных решений. б) 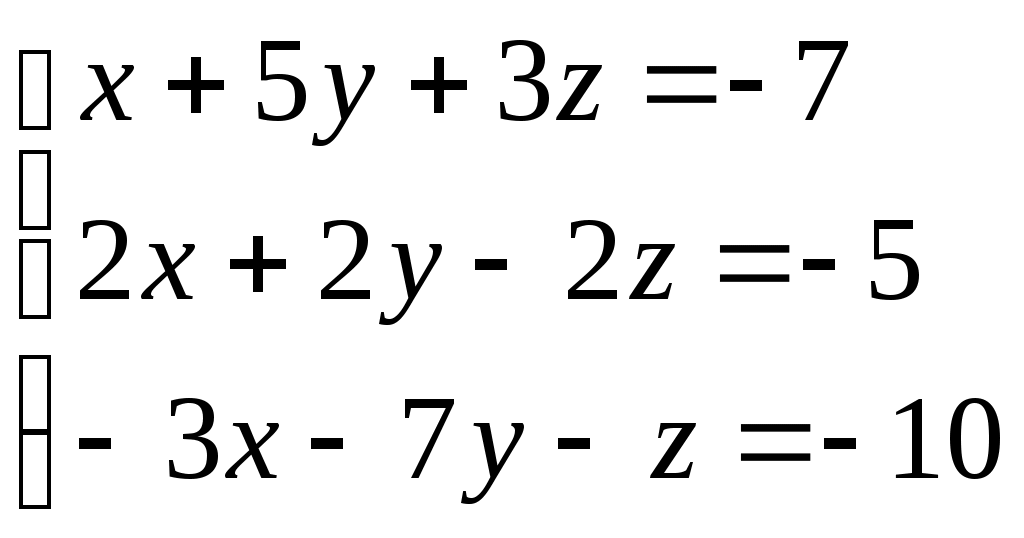 Составим расширенную матрицу системы и приведем ее к ступенчатому виду: 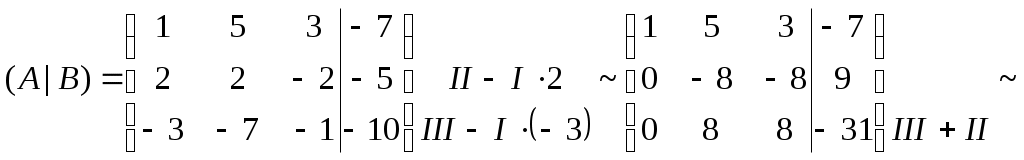 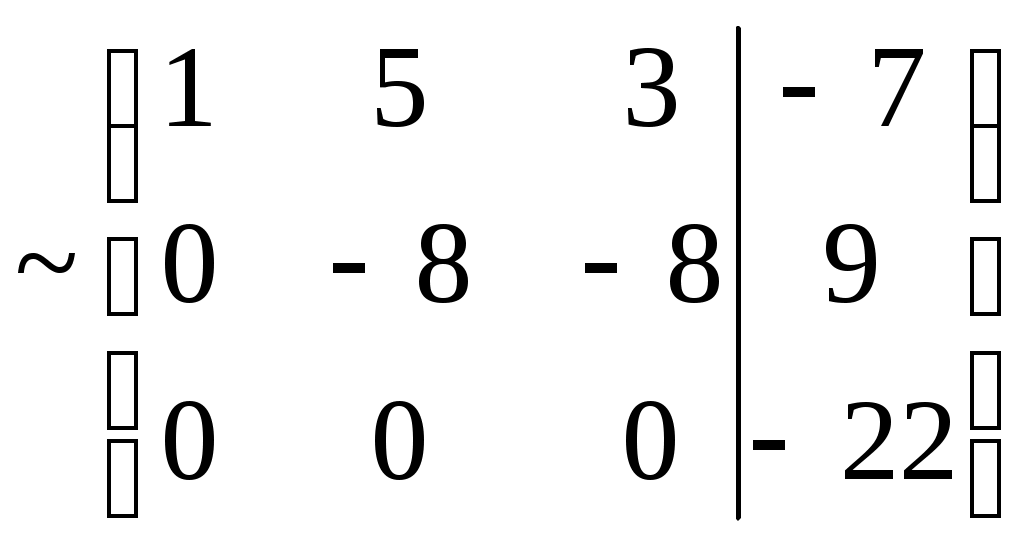 Таким образом,  , а  . Поскольку ранг основной матрицы системы не равен рангу расширенной матрицы системы, то согласно теореме Кронекера-Капелли, система несовместна.1.5.5. Даны вершины пирамиды  ,  ,  ,  . Найти: а) угол между векторами  и  ; б) площадь грани  ; в) проекцию вектора на вектор  ; г) объем пирамиды; д) длину высоты пирамиды, опущенной из вершины  .а) Косинус угла между векторами и найдем по формуле .Запишем координаты векторов:  ,  ,найдем их длины:  ;  Тогда:   б) Площадь грани определим как площадь треугольника :  . Площадь параллелограмма можно определить как модуль векторного произведения, построенного на векторах  и  как на сторонах:  . Запишем координаты векторов:  ,  .Найдем векторное произведение векторов 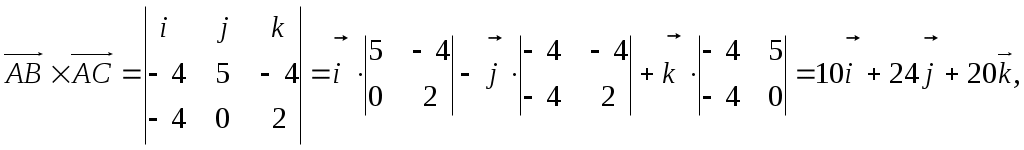 модуль которого равен  .Тогда  .в) Проекцию вектора на вектор найдем по формуле  Запишем координаты вектора :  .Тогда  г) Объем пирамиды  найдем через смешанное произведение векторов по формуле  . Найдем смешанное произведение векторов 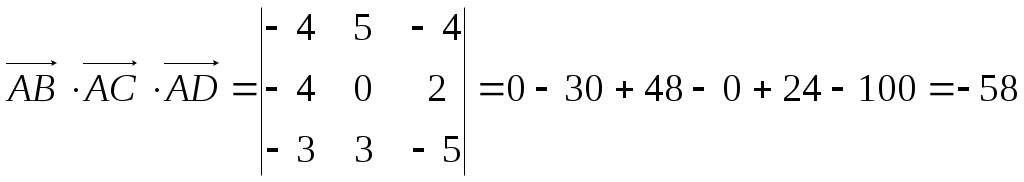 ,  и  : .Тогда искомый объем  .д) Длину высоты пирамиды, опущенной из вершины вычислим как расстояние от точки до плоскости грани .Расстояние от точки  до плоскости  найдем по формуле  .Составим уравнение плоскости . Уравнение плоскости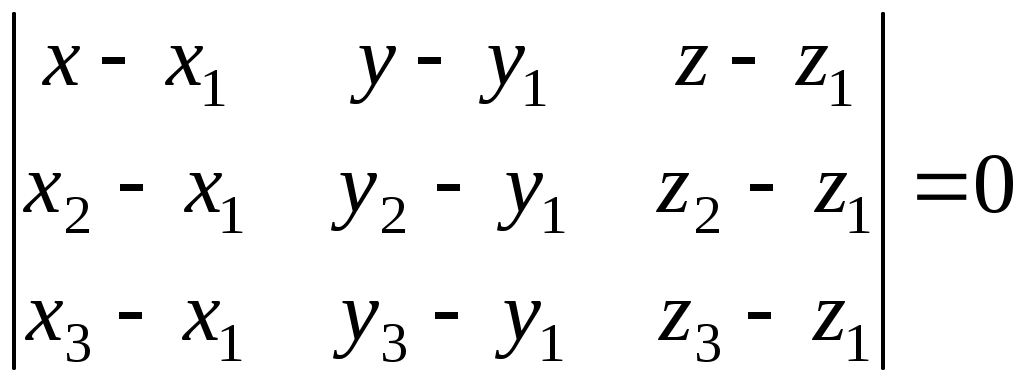, проходящей через три точки  ,  ,  найдем по формуле:  .Подставляя соответствующие координаты точек 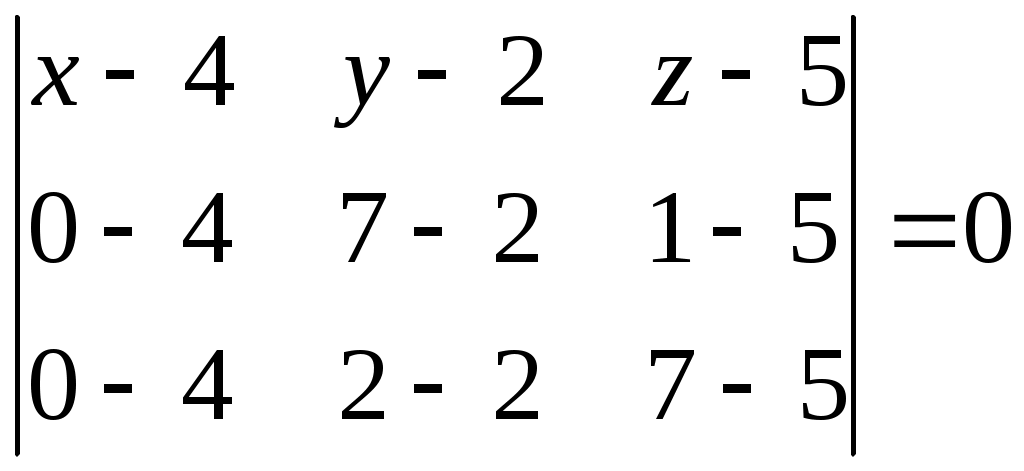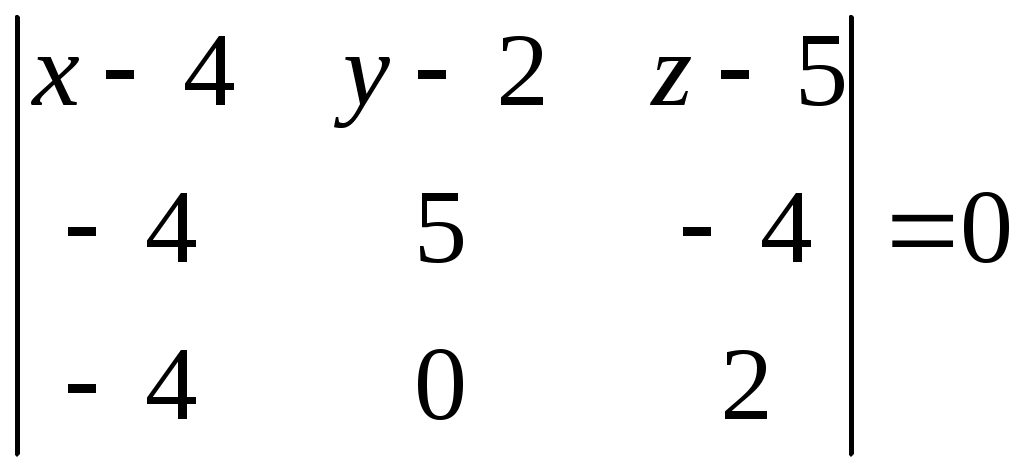, , , получим: ;  ; ;  Таким образом, уравнение плоскости :  .Тогда, расстояние от точки до плоскости равно . |