Контрольная работа_Павлов.М.Д. Контрольная работа 1 Задача Заданы матрицы А, В, С. Найти а б вычислить определитель матрицы А
 Скачать 1.04 Mb.
|
|
2.10.5. Найти плоскую меру множества, ограниченного заданными линиями на плоскости Oxy, сделать чертеж  ,  ,  Плоская мера множества равна площади фигуры, ограниченной указанными линиями. Выполним чертеж: 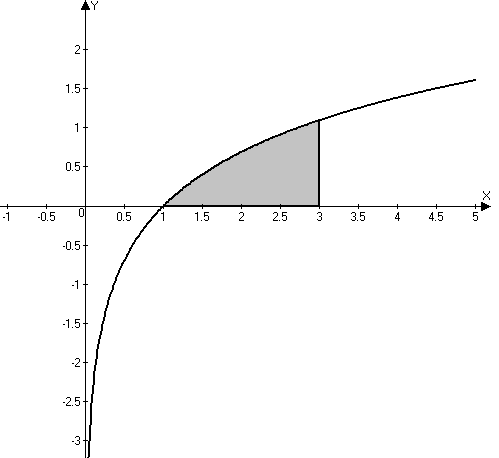 Поскольку при 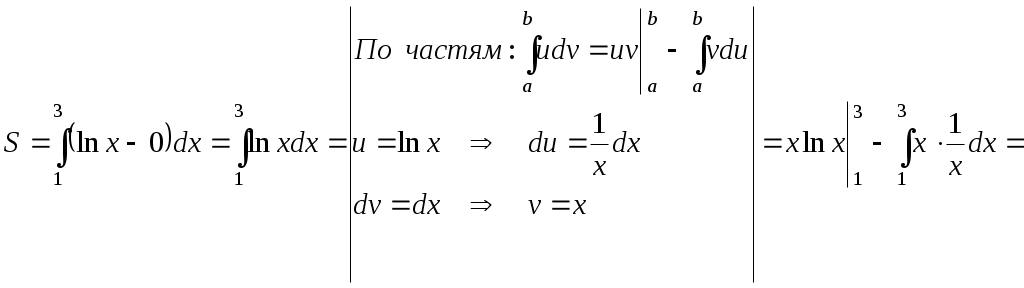 данная фигура ограничена сверху графиком функции , снизу – осью   , то ее площадь равна:  Контрольная работа № 4 3.1.5. Выполнить действия с комплексными числами  ,  ,  в алгебраической форме.Вычислить: 1)  2)  3.2.5. Выполнить действия с комплексными числами  ,  ,  в тригонометрической форме.Вычислить: 1)  ; 2)  ; 3)  ; 4)  Запишем комплексные числа в тригонометрической форме, для этого найдем их модули и аргументы. Так как  ,  , то   Тогда тригонометрическая форма комплексного числа имеет вид .Так как  ,  , то   Тогда комплексное число в тригонометрической форме будет иметь вид: .Поскольку  ,  , то   Таким образом, тригонометрическая форма комплексного числа имеет вид .Теперь выполним действия, используя тригонометрические формы чисел: 1)   2) Запишем комплексное число  в тригонометрической форме: Тогда, тригонометрическая форма комплексного числа  будет име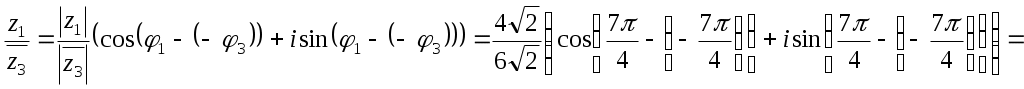ть вид: Получаем:   3) Согласно формуле Муавра  . Тогда  4) Извлекаем корни по формуле Таким образом: 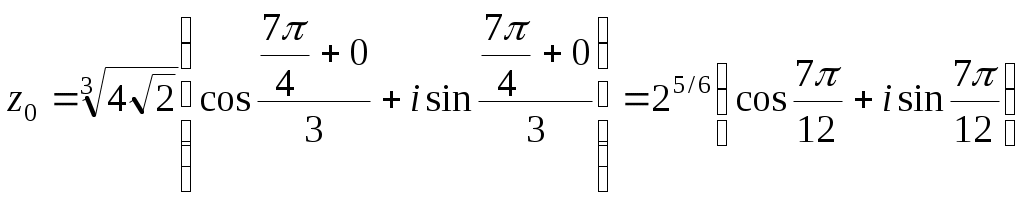 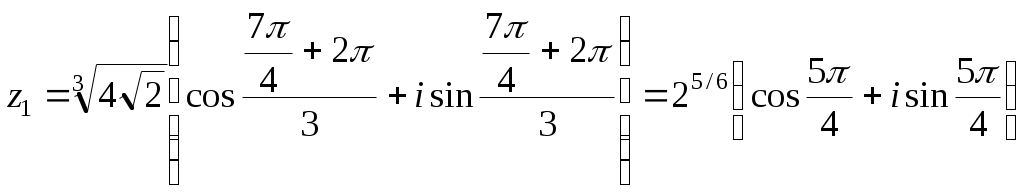 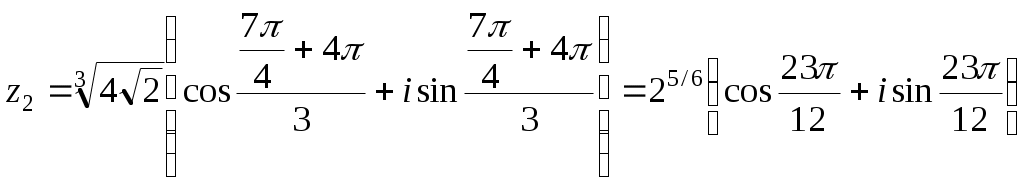    3.3.5. Выяснить, какие линии удовлетворяют условию    Так как  , то  . Найдем модуль этого комплексного числа:  .Тогда условие задачи примет вид: 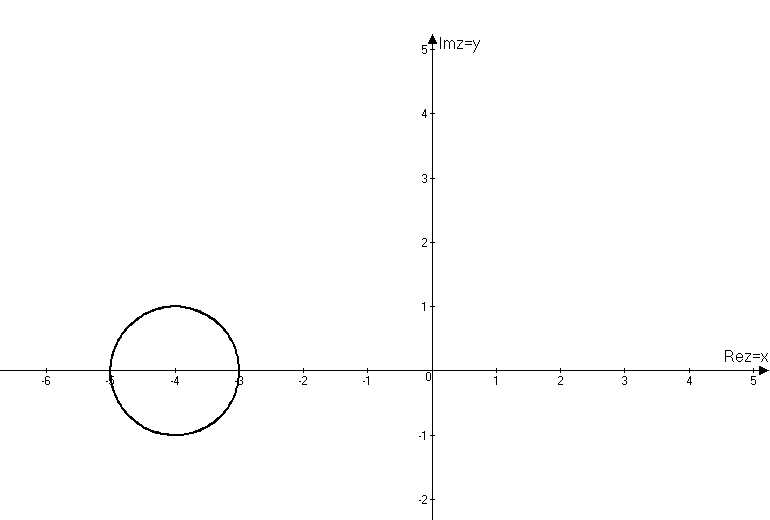 и, возведя в квадрат обе части уравнения, получим:  – уравнение окружности с центром в точке  и радиусом, равным 1. Изобразим эту линию на комплексной плоскости: 3.4.5. Выяснить, какие области удовлетворяют условию  Полагая , получим  . Запишем модуль этого комплексного числа:  .Тогда условие задачи примет вид: 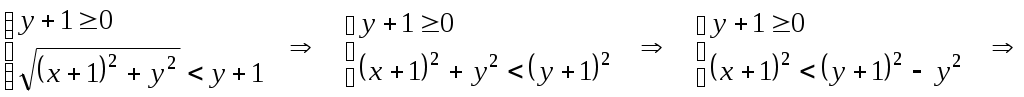 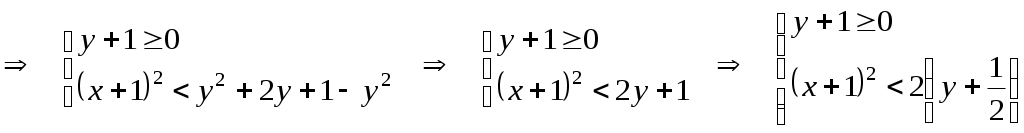. Данное неравенство имеет смысл тогда и только тогда, когда  . Тогда получим:  Границей области 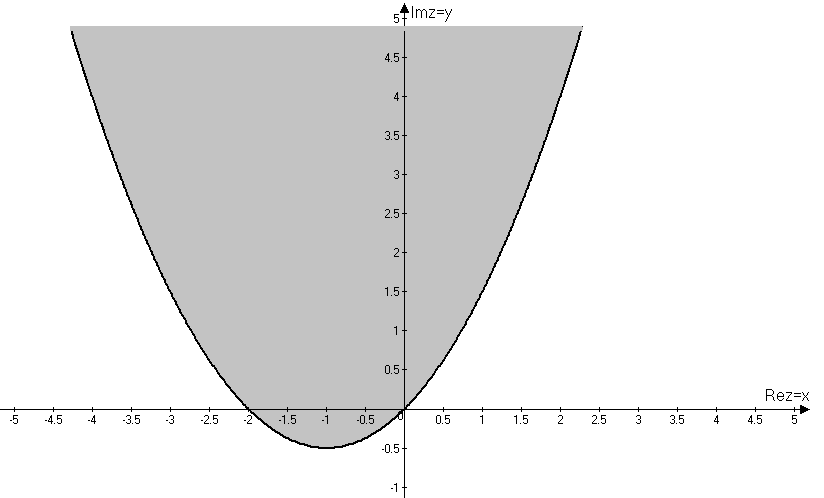 является парабола  с вершиной в точке  . Сама область расположена внутри параболы: 3.5.5. Вычислить производную функции  в точке   ,  Найдем производную:  .Теперь вычислим значение производной в точке : 3.6.5. Решить систему линейных уравнений с комплексными коэффициентами. 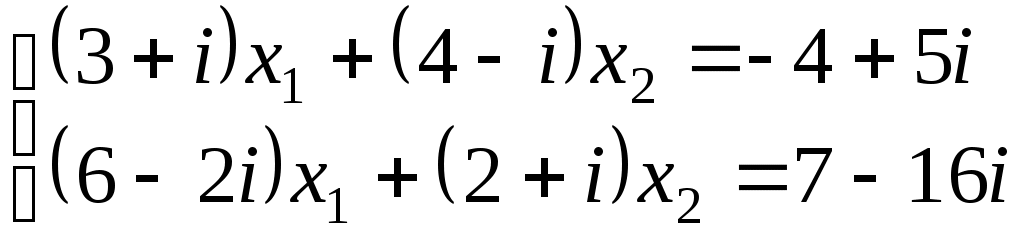 Решим систему по формулам Крамера. Найдем главный определитель системы:   .Найдем определители  :    Далее, по формулам Крамера, находим неизвестные:     |