Кр. кр 1 вар 1. Контрольная работа 1 Задание 1 а Вычислите матрицу A б найдите матрицу, обратную к матрице a
 Скачать 288.79 Kb. Скачать 288.79 Kb.
|
|
Контрольная работа №1 Задание 1 а) Вычислите матрицу A; б) найдите матрицу, обратную к матрице A . 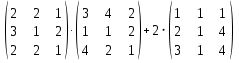 Решение: а) Вычислите матрицу A Выполним умножение матриц: 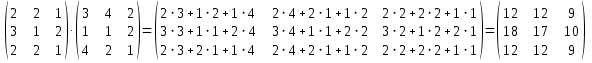 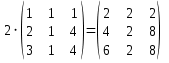 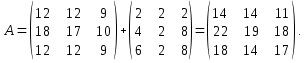 б) Найдем обратную матрицу, к матрице А. 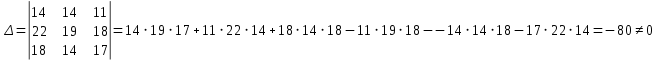 обратная матрица существует. обратная матрица существует.Транспонируем матрицу А 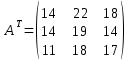 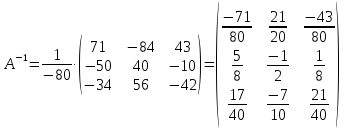 Задание 2. Решите систему линейных уравнений методом Гаусса, Крамера и обратной матрицы 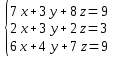 Решение: Решите систему линейных уравнений методом Гаусса, составим расширенную матрицу системы: 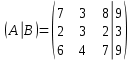 Согласно алгоритму Гаусса будем приводить эту матрицу к треугольному виду 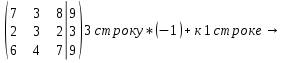 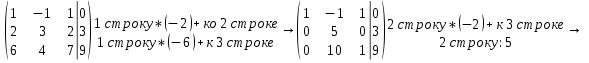 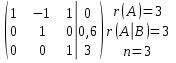 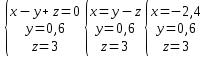 Решим систему по правилу Крамера: 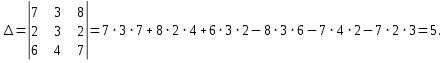 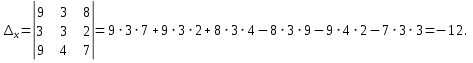 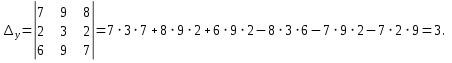 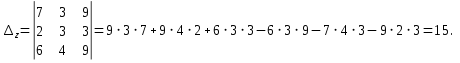 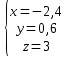 Решим систему методом обратной матрицы: Найдем обратную матрицу, к матрице А. 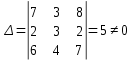 обратная матрица существует. обратная матрица существует.Транспонируем матрицу А 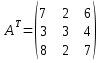 Найдём алгебраические дополнения транспонированной матрицы 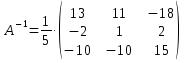 Найдем решение: 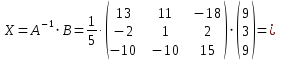 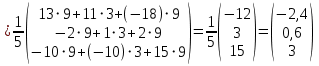 Задание 3 Даны точки A, B, C на плоскости.
Решение: a) Найдём уравнение прямой, проходящей через две точки: 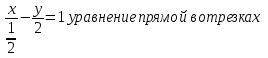 Составим параметрические уравнения данной прямой: b) Найдем длину отрезка c) Найдем уравнение прямой, перпендикулярной прямой AB и проходящей через точку C. СН – искомая прямая. Уравнение прямой, проходящей через точку и направляющий вектор: d) Найдем уравнение прямой, параллельной прямой AB и проходящей через точку C. СМ искомая прямая e) Найдем длину перпендикуляра, опущенного на прямую AB из точки C. Уравнение прямой f) Найдите косинус угла ACB. g) Найдем площадь треугольника ABC. 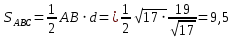 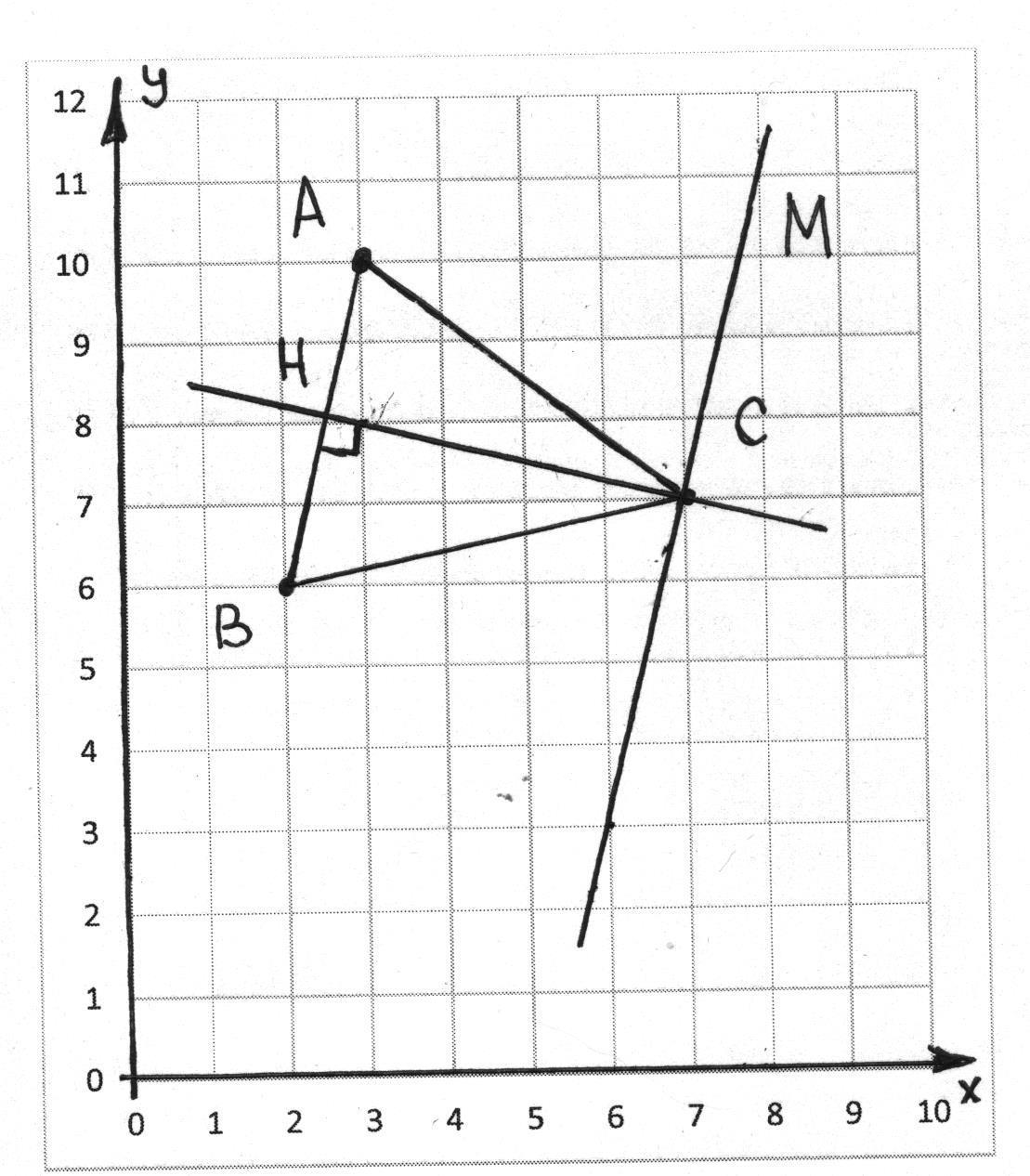 Задание 4 Дана кривая второго порядка. Решение: Приведём кривую второго порядка к каноническому виду. Выделяем полные квадраты 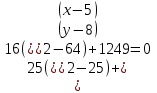 (5;8) центр симметрии, a=4, b=5. Т.к. b>a Найдем эксцентриситет кривой. Найдите уравнения директрис. Найдем координаты фокусов кривой. Асимптот нет Чертёж. 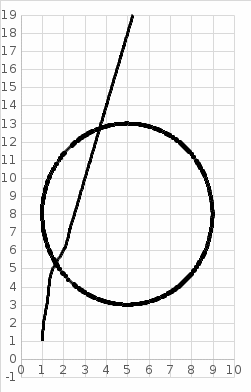 Задание 5 Найти пределы функций, не пользуясь правилом Лопиталя. 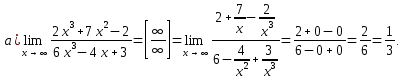 Домножим числитель и знаменатель дроби на сопряженное по формуле: 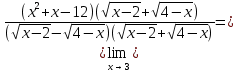 Разложим 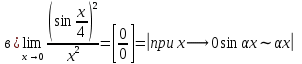 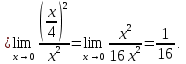 Применим второй замечательный предел: Пусть 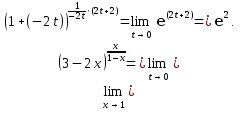 Задание 6 Задана функция 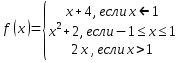 Решение: При Проверим выполнение равенства: 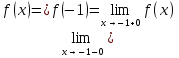 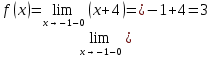 3=3=3, значит х=-1 не является точкой разрыва. При Проверим выполнение равенства: 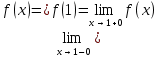 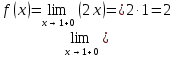 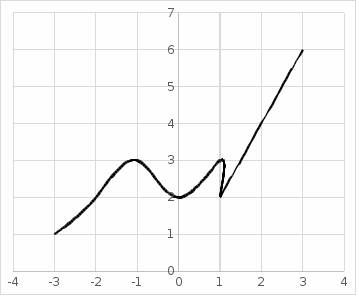 | |||||||||||||||||||||||
