Ч АСТЬ 1 АСТЬ 1 |

|
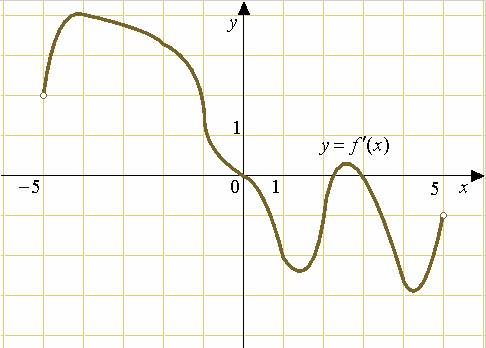
5. На рисунке изображен график производной функции: y = f '(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции.
В ответе укажите длину наибольшего из них.
|
|
1. На рисунке изображён график
функции y = f(x) и касательная к
нему в точке с абсциссой x0.
Найдите значение производной
функции в точке х0.
|
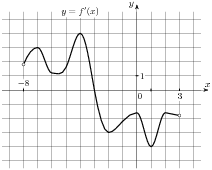
2. На рисунке изображен график
производной функции: y = f '(x),
определенной на интервале (-8; 3).
В какой точке отрезка [-2; 1]
функция f(x) принимает
н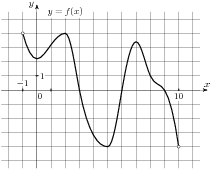 аименьшее значение. аименьшее значение.
|
|
6. На рисунке изображен график производной функции:
y = f '(x) , определенной на интервале (- 5; 5).
Найдите количество точек, в которых касательная к графику функции параллельна прямой у = - 2х – 7 или совпадает с ней.
|
|

|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-1;10).
Найдите количество точек, в которых касательная к графику функции параллельна прямой
у = -20.
| ЧАСТЬ 2 |
7. Найдите наибольшее значение функции
у = 12 √ 2 cos x + 12х – 3π + 9 на отрезке [ 0; π/2]
8. Найдите точку минимума функции у = 2х – ln ( х + 3) + 7.
|
4. На рисунке изображен
график производной
функции: y = f '(x),
определенной на интервале
(-7; 14).
Найдите количество
точек минимума функции
на отрезке [-6; 13].
|
| ЧАСТЬ 3 |
9. Построить график функции у = х3 + 3х2 – 4
1.б) Составить уравнение касательной к графику функции f(х) = х4 – 3х2 + 5х – 17 в точке с абсциссой х0 = -1.
|
Алгебра – 10 Контрольная работа № 10 по теме: «Производная» Вариант 2  |
Ч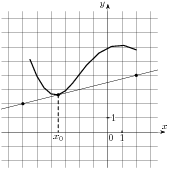 АСТЬ 1 АСТЬ 1 |
|
5. На рисунке изображен график производной функции: y = f '(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции.
В ответе укажите длину наибольшего из них.
|
|
1. На рисунке изображён график
функции y = f(x) и касательная к
нему в точке с абсциссой x0.
Найдите значение производной
функции в точке х0.
|
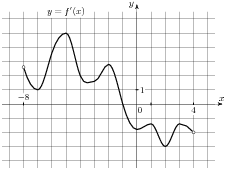
2. На рисунке изображен график
производной функции: y = f '(x),
определенной на интервале (-8; 4).
В какой точке отрезка [0; 3]
функция f(x) принимает
н аименьшее значение. аименьшее значение.
|
|
|
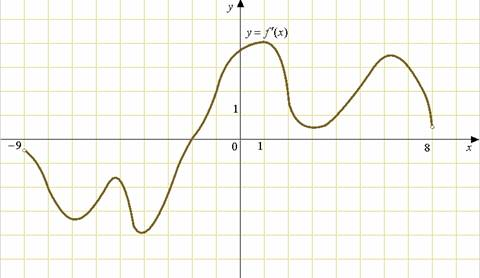
6. На рисунке изображен график производной функции:
y = f '(x) , определенной на интервале (-9; 8). Найдите количеств о точек, в которых касательная к графику функции параллельна прямой
у = - 2х – 7 или совпадает с ней.
|

|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8).
Найдите количество точек, в которых касательная к графику функции параллельна прямой
у = 4.
| ЧАСТЬ 2 |
7. Найдите наименьшее значение функции
у = 2 sin х – 25х + 9 на отрезке [ - 3π/2; 0]
8. Найдите точку максимума функции у = ( х2 – 10х + 10 ) е 5 – х .
|
4. На рисунке изображен
график производной
функции: y = f '(x),
определенной на интервале
(-4; 16).
Найдите количество
точек максимума функции
на отрезке [-3; 15].
|
| ЧАСТЬ 3 |
9. Построить график функции у = – х3 – 3х2 + 3
1.Составить уравнение касательной к графику функции f(х) = х3 – 5х в точке с абсциссой х0 = 2.
|
 Скачать 213.81 Kb.
Скачать 213.81 Kb.