Контрольная работа 2 Динамика. Минобрнауки рф. Фгбоу впо. ТулГУ. Контрольная работа по введению в физику (семестр 1)
 Скачать 322 Kb.
|
|
Контрольная работа №2 Динамика. Минобрнауки РФ. ФГБОУ ВПО. ТулГУ. Контрольная работа по введению в физику (семестр 1) Вариант №1 1.1. П  ерпендикулярно однородному тонкому стержню массы mи длиной lпроходят две параллельные оси. Одна проходит через конец стержня А, а другая через точку О, лежащую на расстоянии х от точки А. На сколько отличаются моменты инерции стержня относительно этих осей? m = 3 кг, l = 4 м, х = 1 ма) 1 кгм2; б) 3 кгм2; в) 5 кгм2; г) 7 кгм2; д) 9 кгм2. Дано: m = 3 кг l = 4 м х =1м  Решение: Момент инерции относительно центра масс  Момент инерции относительно т О рассчитаем с помощью теоремы Штейнера  поскольку здесь  - расстояние между осями, то предыдущую формулу запишем в виде  Изменение моментов тогда равно  Вычислим  ответ б) 3 кгм2 1.2. И 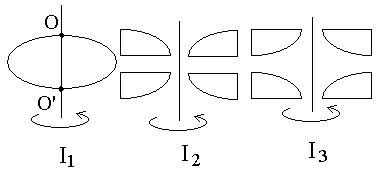 з жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.а) не хватает данных б)  в)  г)  решение второй и третий моменты инерции не отличаются, так как их центры масс находятся на одинаковом расстоянии до оси вращения, но эти моменты инерции больше первого (опять же потому что центр масс находится дальше от оси вращения) ответ г) 1.3. Частица движется в плоскости так, что ее импульс зависит от времени по закону  , где  – постоянные величины,  – единичные орты в декартовой системе координат. Найти тангенс угла между осью y и вектором силы, действующей на частицу в момент времени  с, если  с.А = 3  , В = 4 . а) 0,37; б) 0,47; в) 0,57; г) 0,67; д) 0,77 ;Решение За вторым законом Ньютона в импульсной форме   Продифференцируем выражение для импульса по времени  Искомый угол равен отношению игрековой проекции силы к игрековой 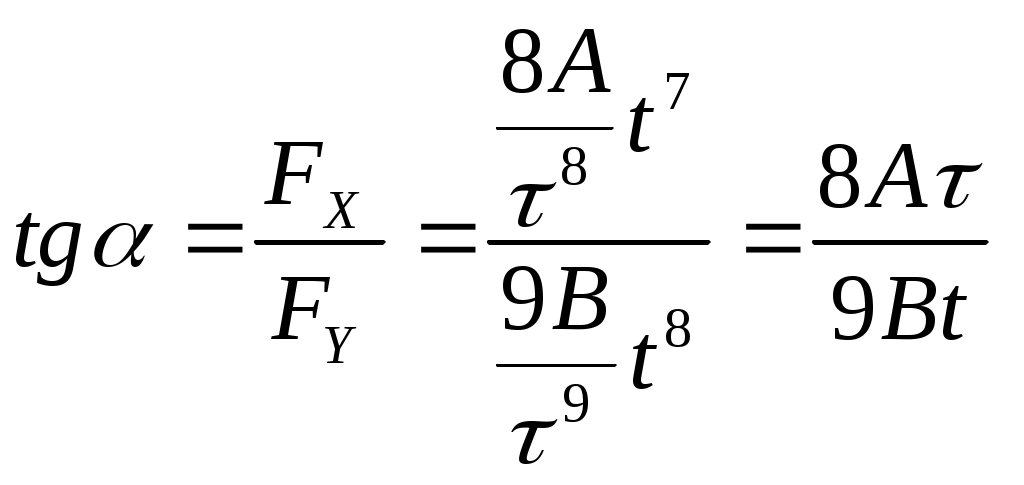 Подставим числа 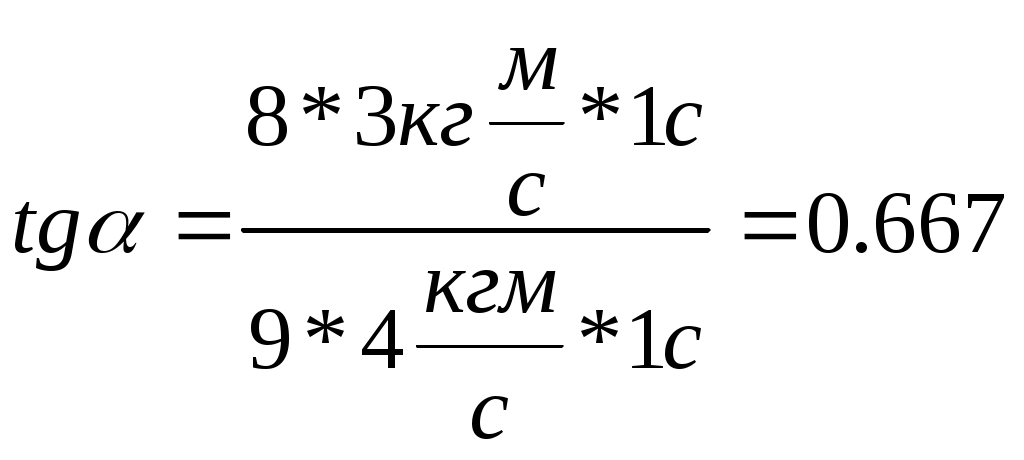 ответ г) 0,67; 1.4. Частица движется в плоскости под действием силы, которая зависит от времени по закону  , где – постоянные величины, – единичные орты в декартовой системе координат. Найти модуль изменения импульса за интервал времени  с, если с. А = 4 Н, В = 5 Н.а) 1,92 кг*м/с; б) 0,92 кг*м/с; в) 0,82 кг*м/с; г) 0,72 кг*м/с; д) 0,62 кг*м/с; дано 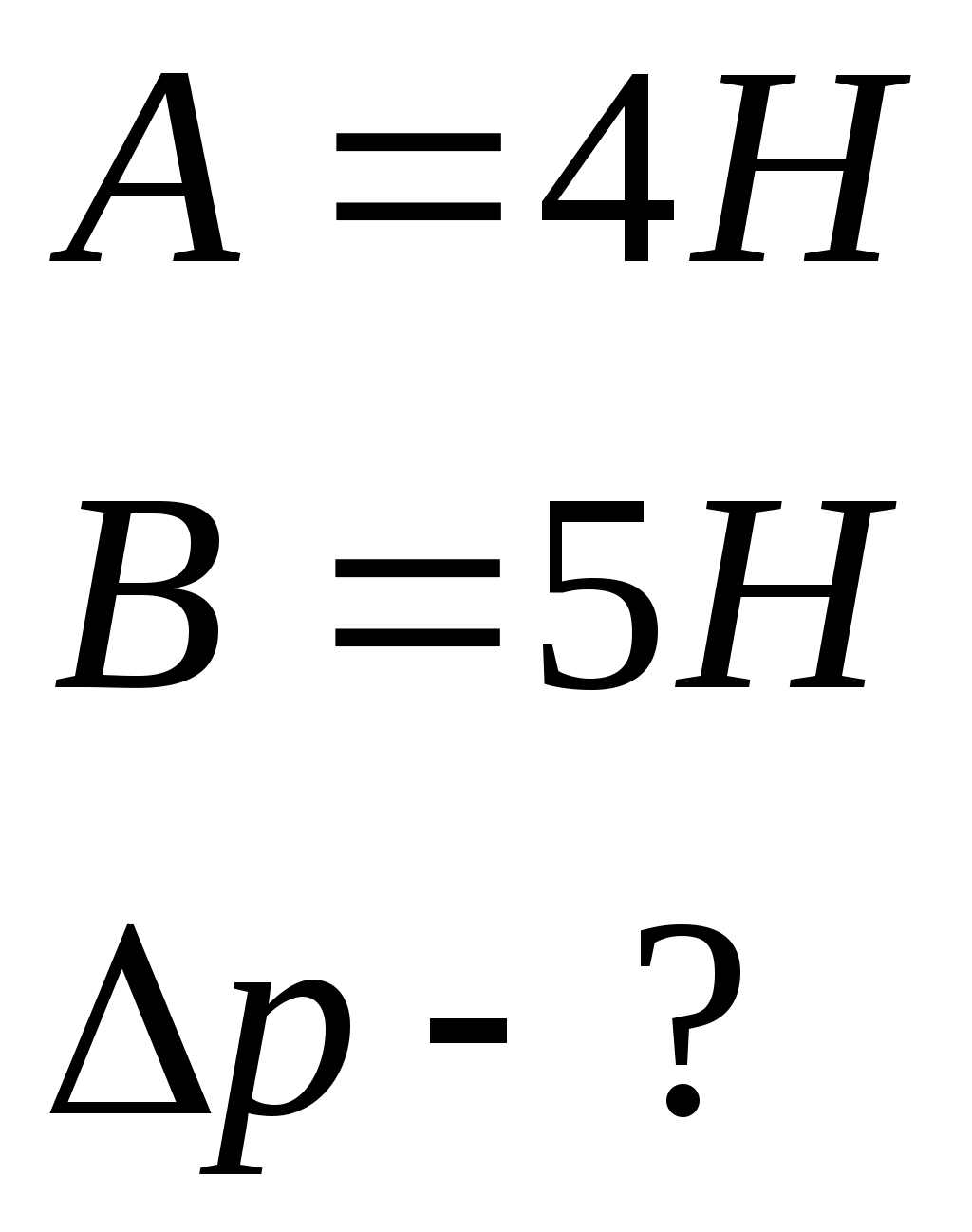 Решение Из закона Ньютона в импульсной форме  Подставим сюда зависимость силы от времени  Проинтегрируем  Имеем  Модуль изменения импульса – это длина полученного вектора  Вычислим  ответ в) 0,82 кг*м/с 1.5. Н 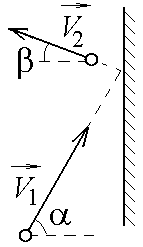 ебольшой шарик массы m летит со скоростью  под углом = 60 к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью  под углом =30 к горизонту. Время соударения . Найти модуль средней силы трения шарика о стену. 8 м/с,  5 м/с, = 0,01 с, m= 3 кг.а) 128 Н; б) 228 Н; в) 328 Н; г) 1328 Н; д) 3328 Н ; Дано 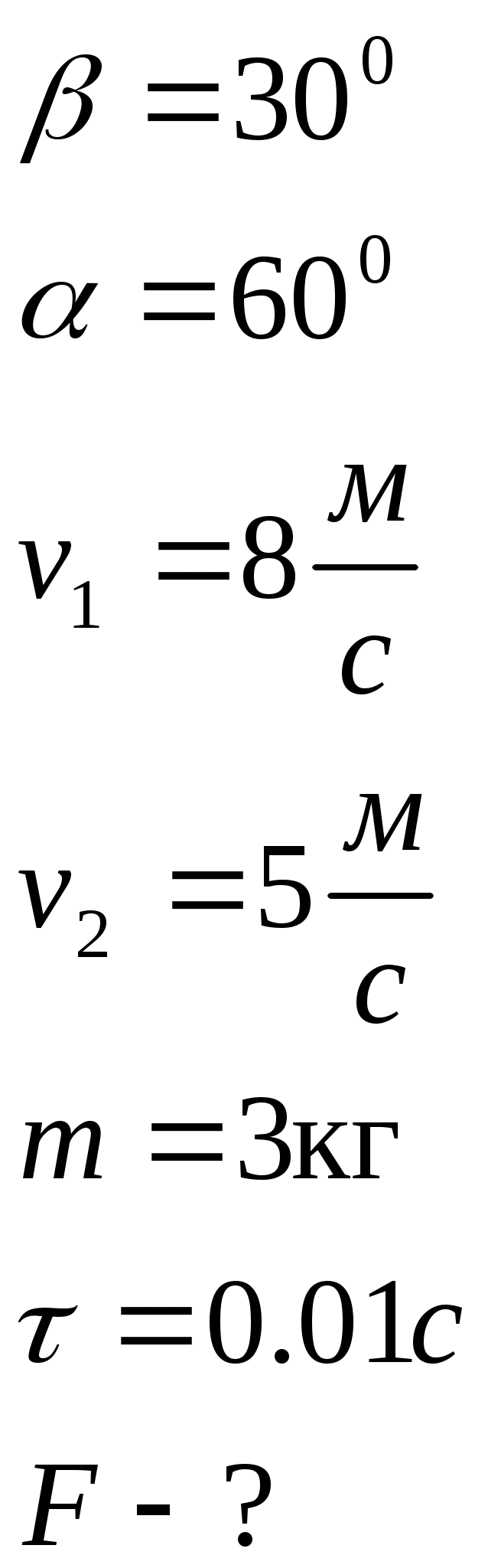  Решение изменение импульса в проекции на вертикальную ось  изменение импульса тела равно импульсу силы  отсюда искомая сила трения  Вычислим 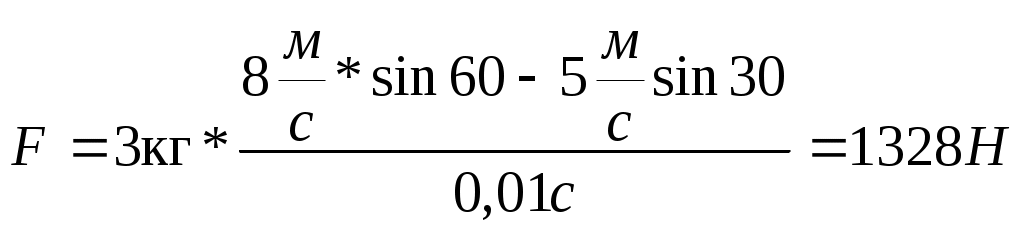 ответ г) 1328 Н 1.6. Т  онкий однородный стержень массы m и длины lможет вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом к стержню прикладывают силу  . Найдите угловое ускорение стержня в начальный момент времени. m= 2 кг, l= 3 м, = 30, F = 4 Н.а) 2 рад/с2; б) 4 рад/с2; в) 6 рад/с2; г) 8 рад/с2; д) 10 рад/с2; дано 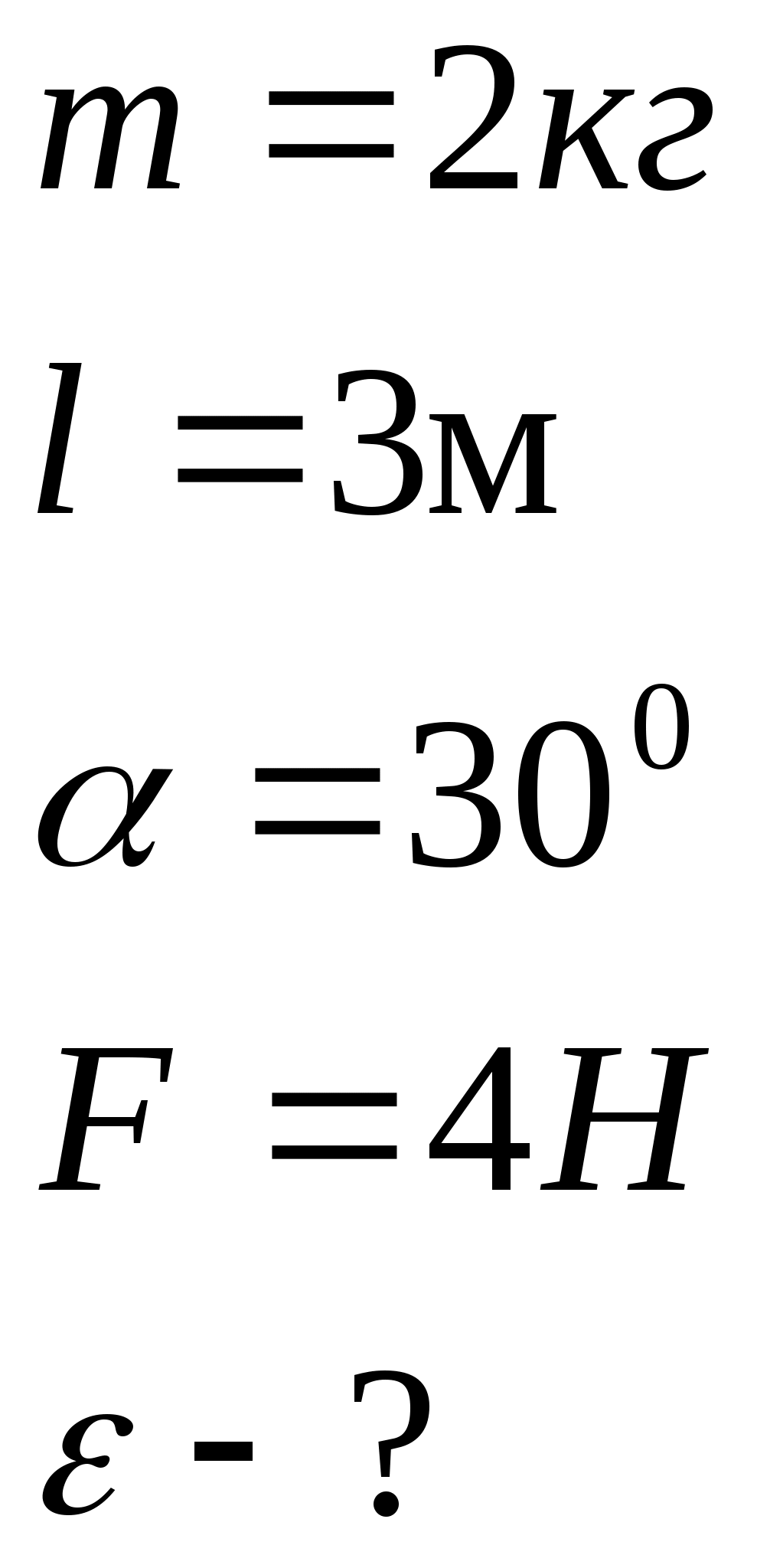 решение запишем закон динамики вращательного движения  подставим сюда момент силы  и момент инерции стержня  получим  отсюда угловое ускорение  вычислим  ответ а) 2 рад/с2; 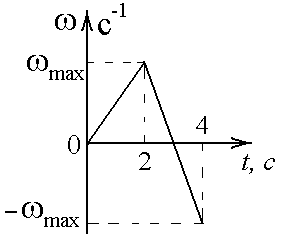 1.7. Тело вращается вокруг закрепленной оси с угловой скоростью, зависимость от времени которой задается графиком. Момент инерции тела относительно оси вращения равен I. На сколько отличаются модули моментов сил, действующих на тело в моменты времени  с и  с. 2 с–1, I = 3  а) 1 Нм; б) 3 Нм; в) 5 Нм; г) 7 Нм; д) 9 Нм; решение угловое ускорение на протяжении первых двух секунд  На протяжении вторых двух секунд (от 2 до 4 секунд)  Запишем для двух промежутков с постоянными угловыми ускорениями уравнения динамики вращательного движения  и  Отсюда разность модулей моментов сил  вычислим  ну а искомое отношение  ответ б) 3 Нм; 1.8. Т 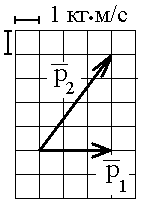 еннисный мяч летел с импульсом  (масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар с средней силой 80 Н. Изменившийся импульс мяча стал равным  . Найти время удара.а) 0,05 с б) 2 с в) 0,5 с г) 0,2 с д) 0,3 с д  ано  решение запишем второй закон Ньютона в импульсной форме  найдем сначала вектор изменения импульса с помощью рисунка  величина этого вектора  время действия силы на мяч  ответ а) 0,05 с 1 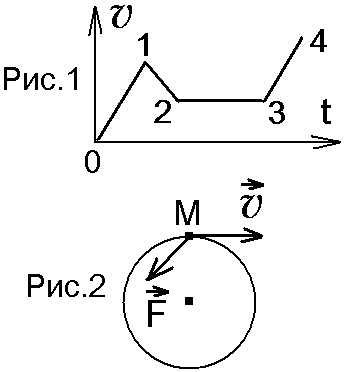 .9. Величина (модуль) скорости материальной точки  , все время движущейся по окружности, меняется со временем по закону, показанному на рис.1. Какому участку этого графика соответствуют указанные на рис.2 направления скорости  и силы , действующей на точку M?а) 0–1 б) 1–2 в) 2–3 г) 3–4 решение горизонтальная проекция силы противоположно направлена к вектору скорости поэтому скорость убывает под действием этой силы (ее момента) ответ б) 1–2 1.10. Д  ва одинаковых однородных тонких стержня массой mи длиной l каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О. l = 2 м, m= 3 кг.а) 28 кгм2; б) 26 кгм2; в) 24 кгм2; г) 22 кгм2; д) 20 кгм2. дано 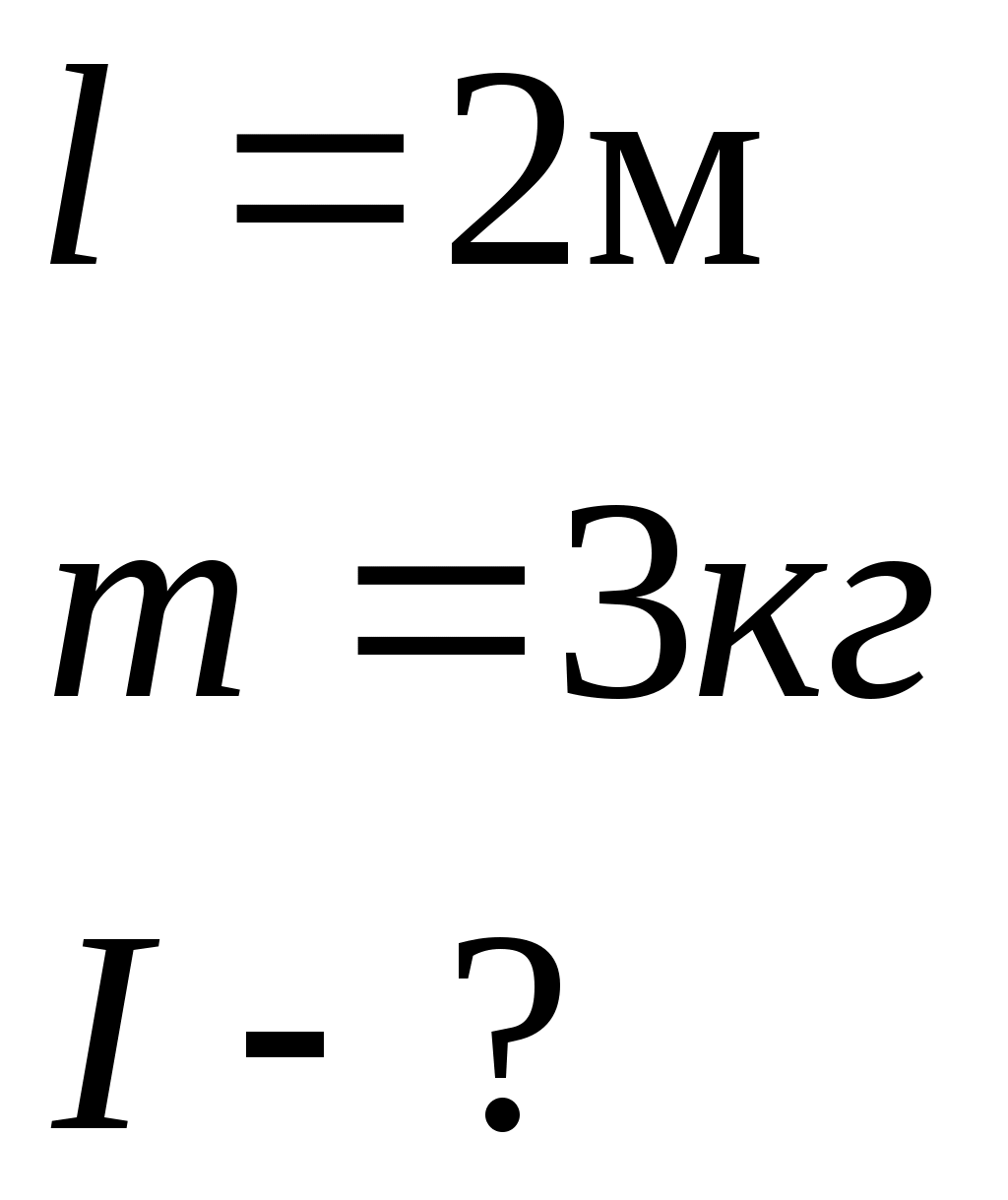  решение момент инерции вертикальной части (стержень)  момент горизонтального (относительно центра масс)  а относительно точки О за теоремой Штейнера  за теоремой Пифагора  имеем  общий момент инерции   вычислим  ответ д) 20 кгм2 |