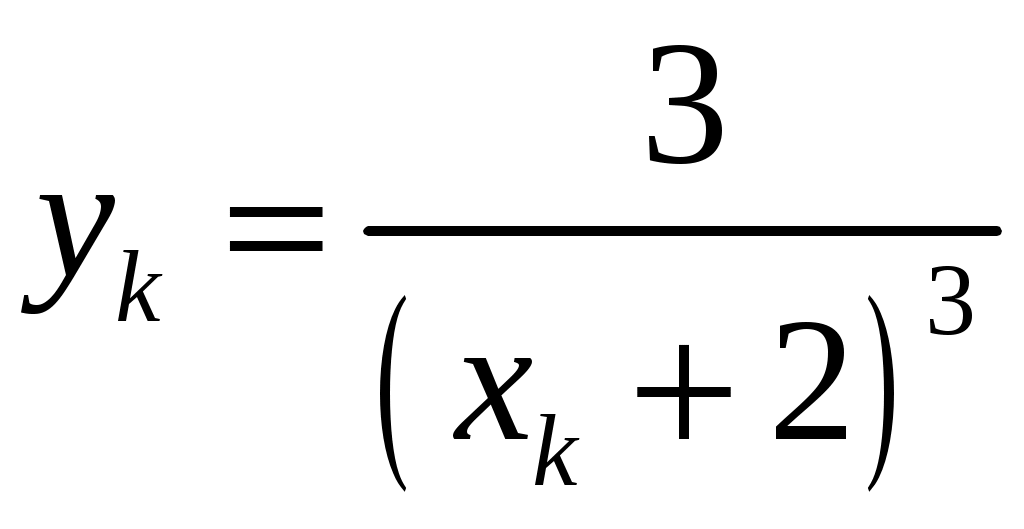Матем кр. 5338725 вар 5 КР. Контрольная работа 2 интегральное исчисление. Дифференциальные уравнения первого порядка задание найти неопределенные интегралы
 Скачать 366 Kb. Скачать 366 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА №2 «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА» ЗАДАНИЕ 1. Найти неопределенные интегралы. 1. 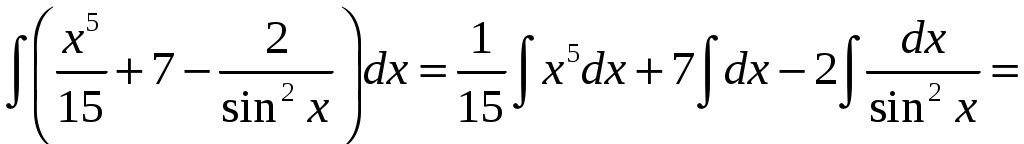 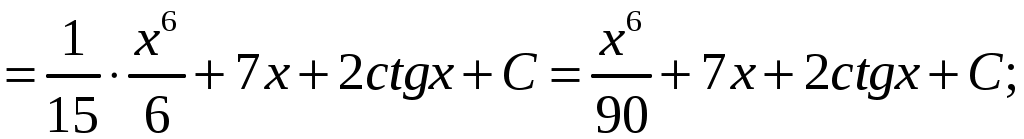 2. 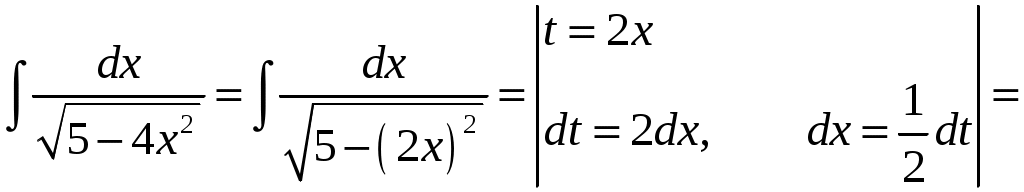 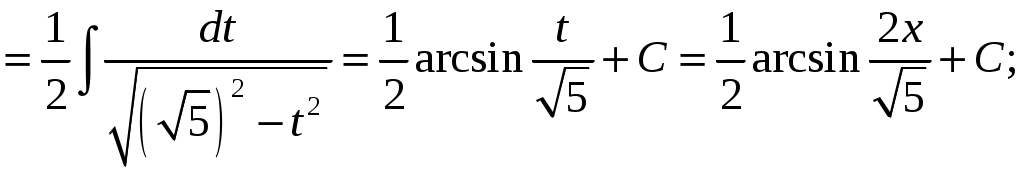 3. 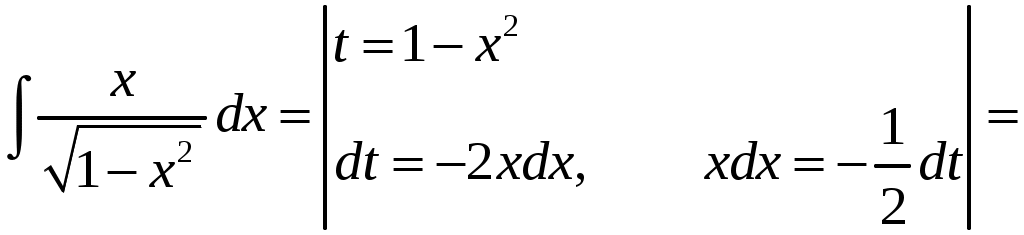 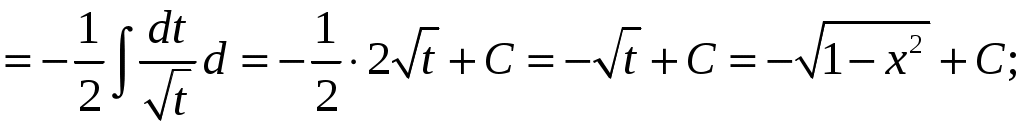 4. 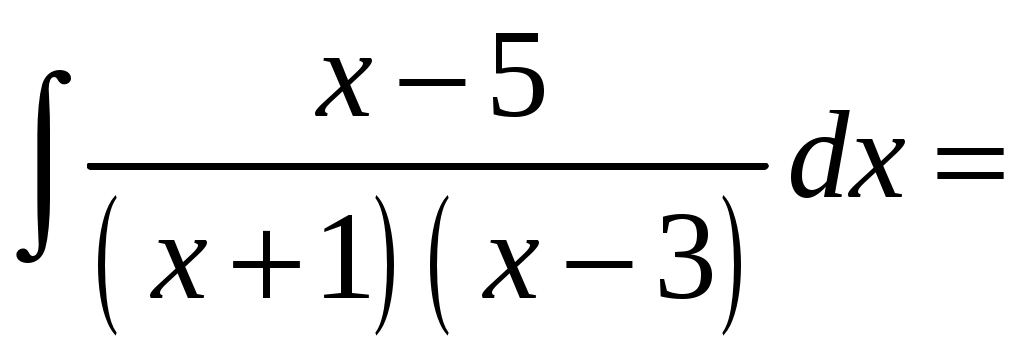 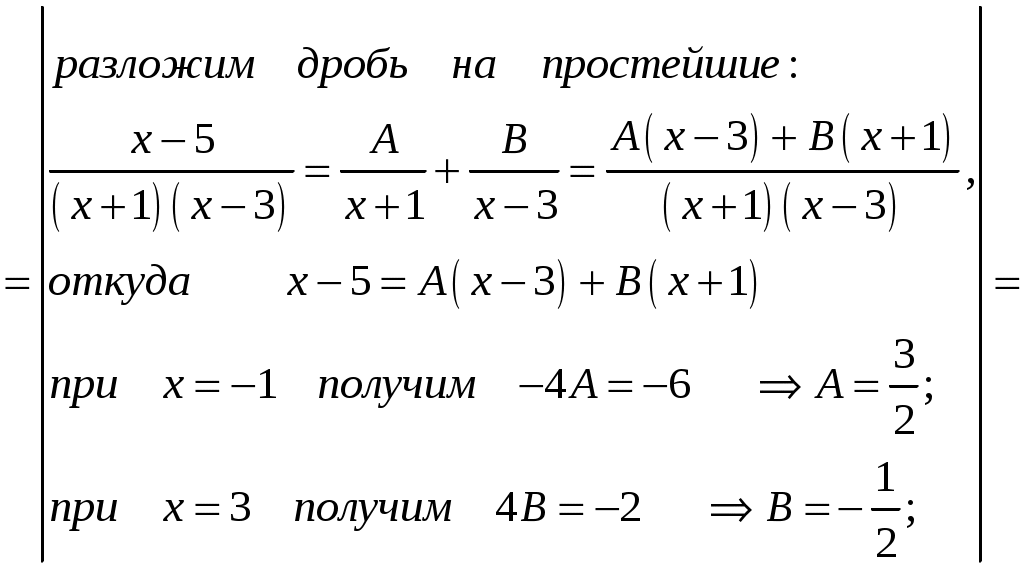 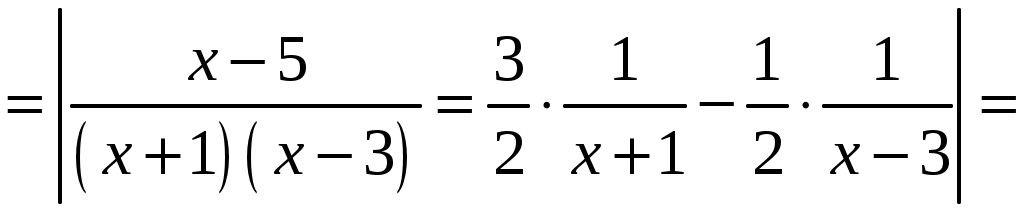 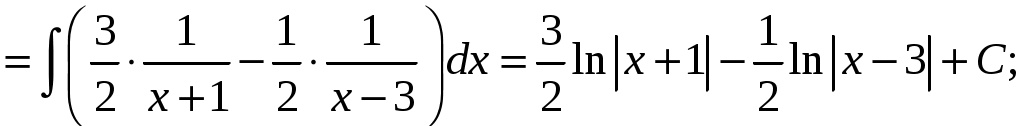 5. 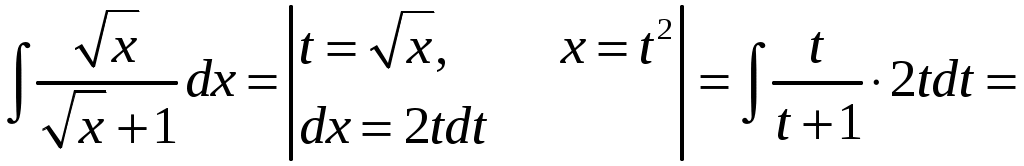 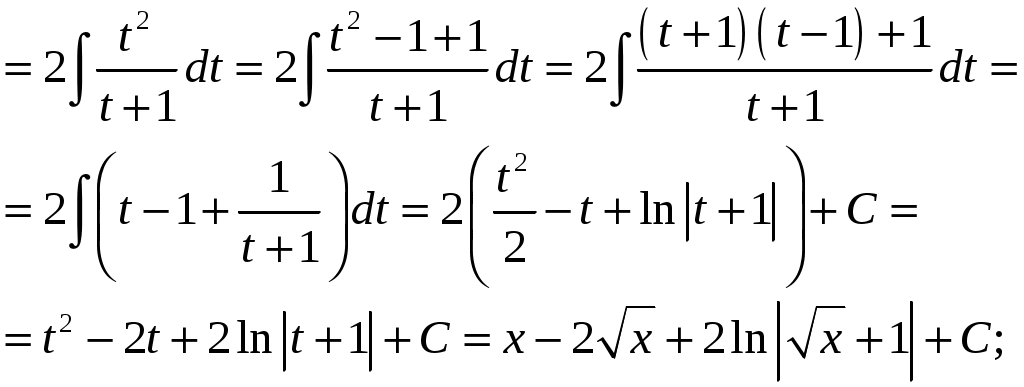 6. 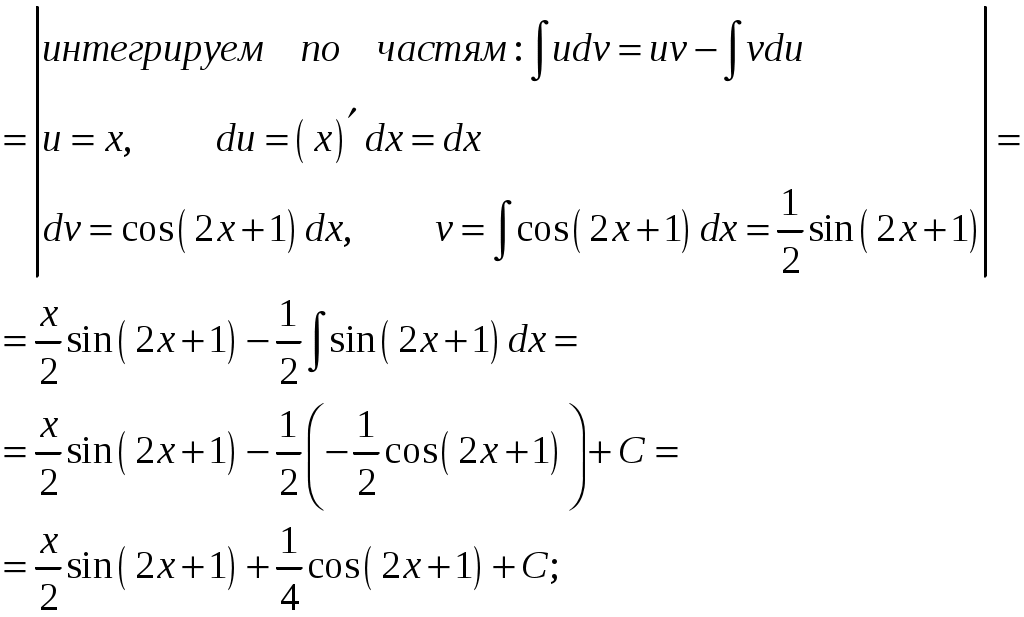 7. 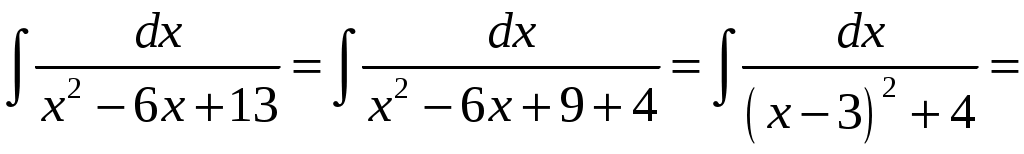 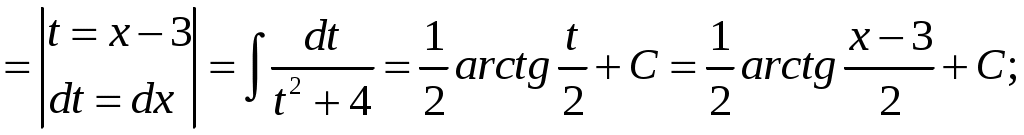 8. 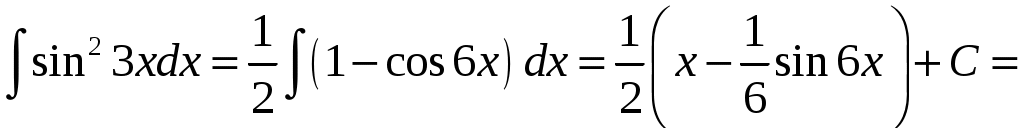 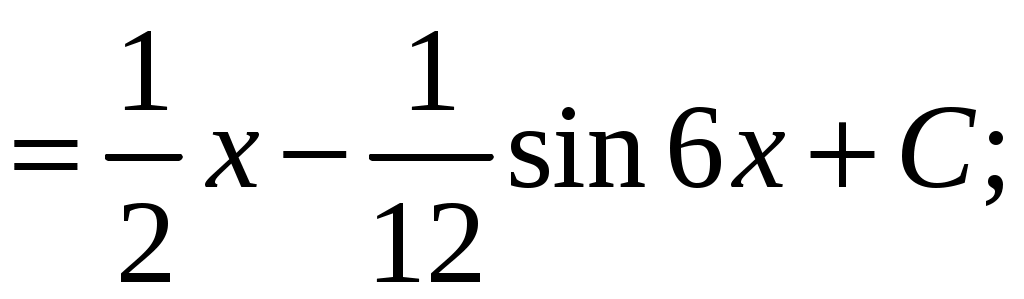 ЗАДАНИЕ 2. Вычислить несобственный интеграл или доказать его расходимость. 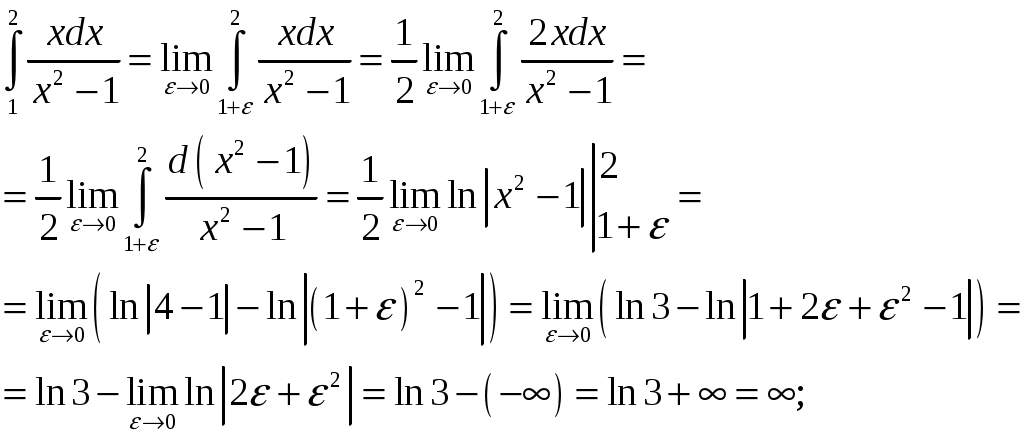 Следовательно, интеграл расходится. ЗАДАНИЕ 3. В декартовой системе координат построить плоскую фигуру, ограниченную линиями. Найти площадь фигуры. Решение. Найдем точки пересечения парабол: 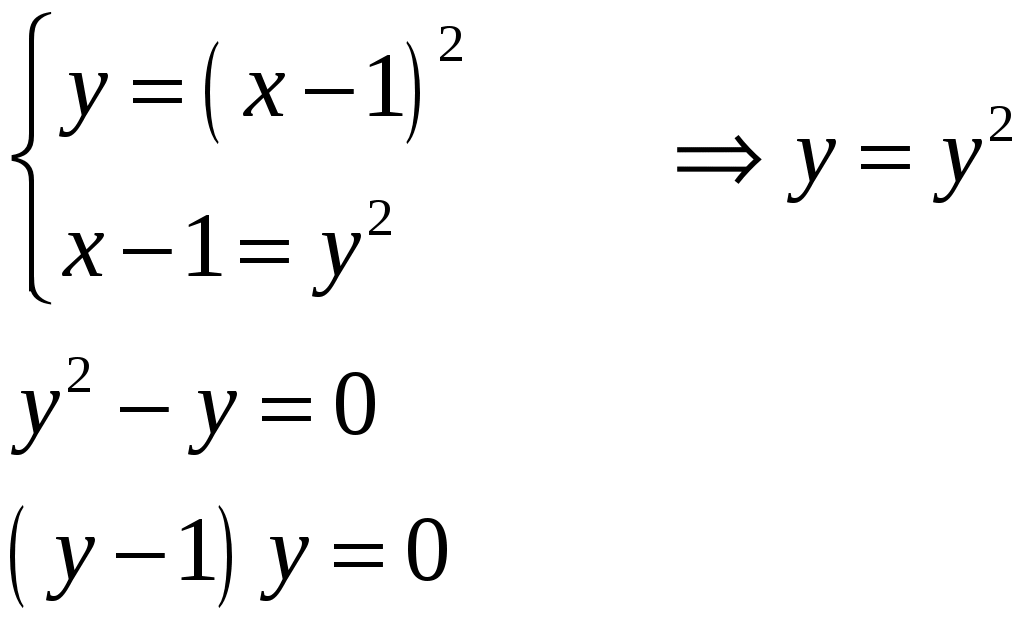 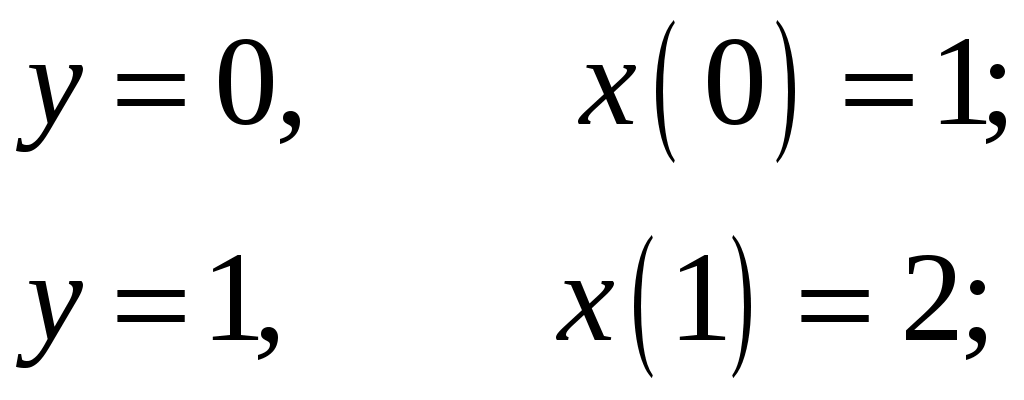 Следовательно, Выполним чертеж. 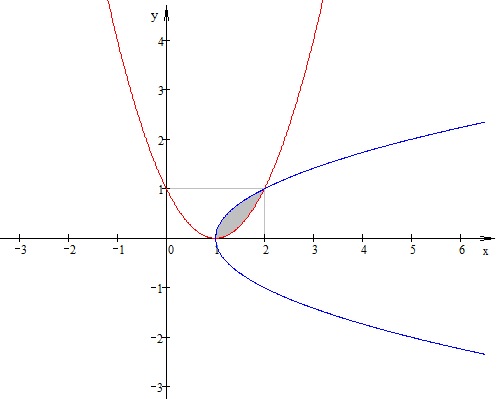 Вычислим площадь: 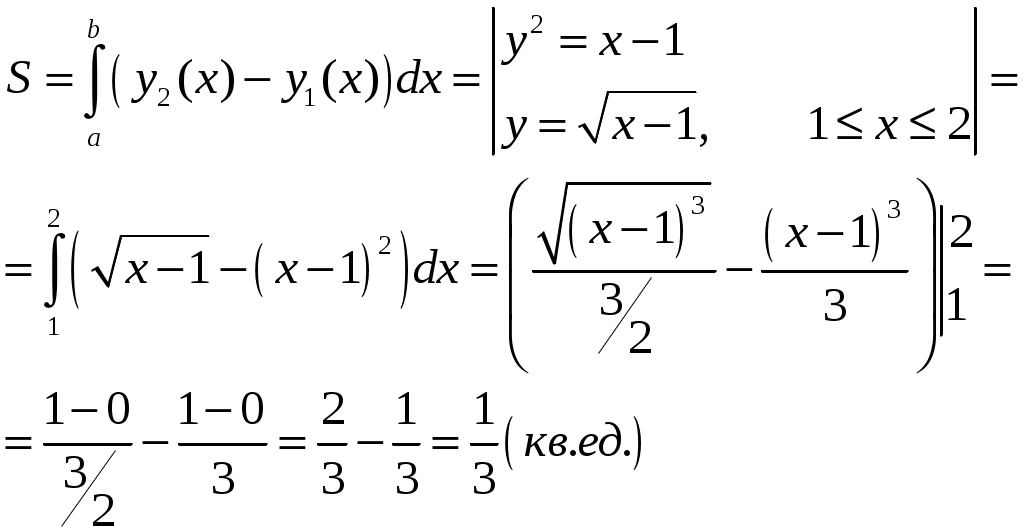 ЗАДАНИЕ 4. Найти объем тела, полученного вращением вокруг оси Решение. 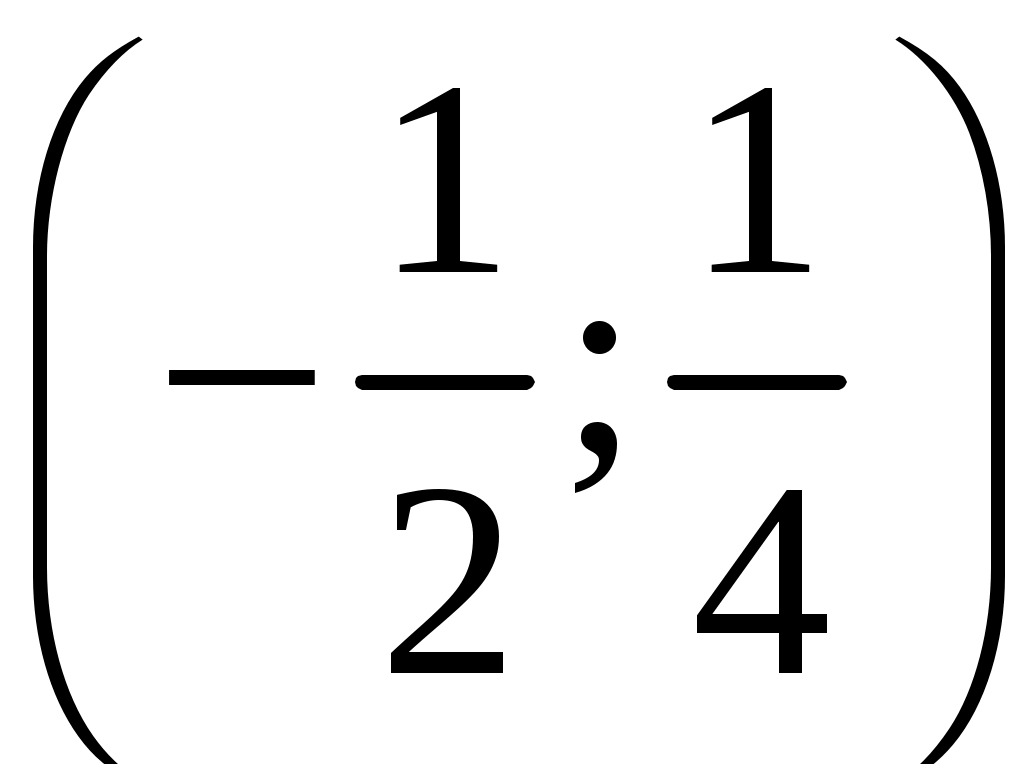 - вершина, - вершина,Выполним чертеж плоской фигуры. 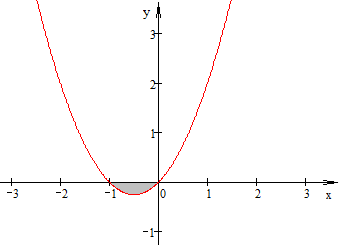 Вычислим объем тела, полученного вращением фигуры вокруг оси 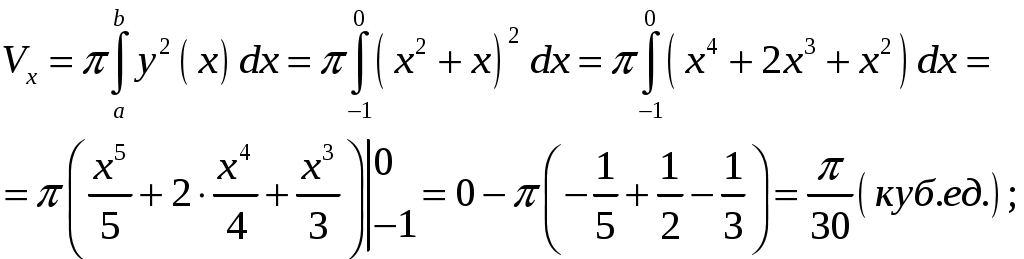 ЗАДАНИЕ 5. Интеграл вычислить точно по формуле Ньютона-Лейбница и приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений. 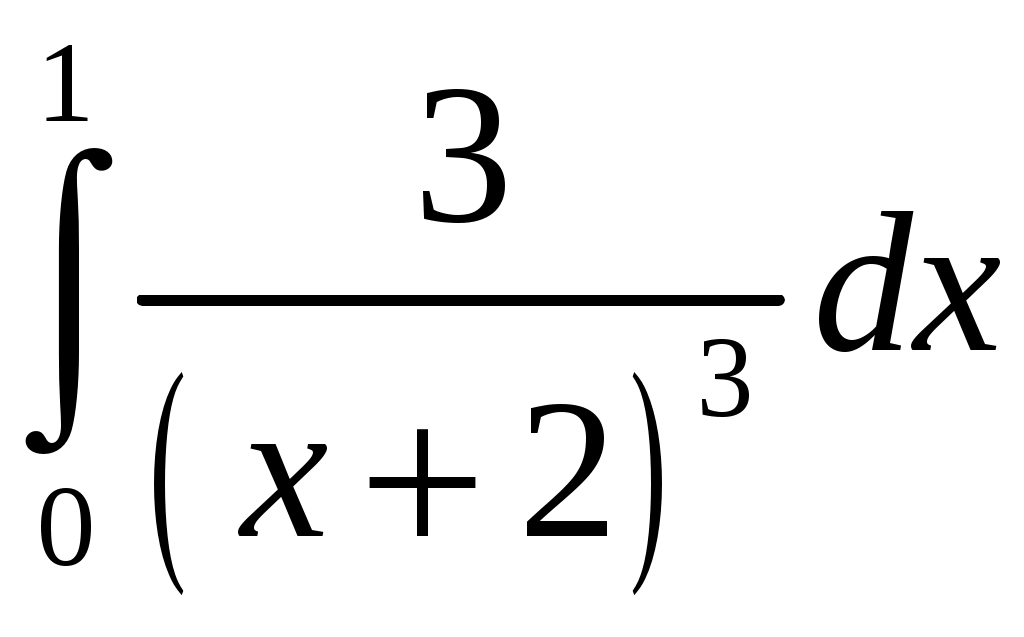 . .Решение. Вычислим интеграл непосредственно по формуле Ньютона-Лейбница: 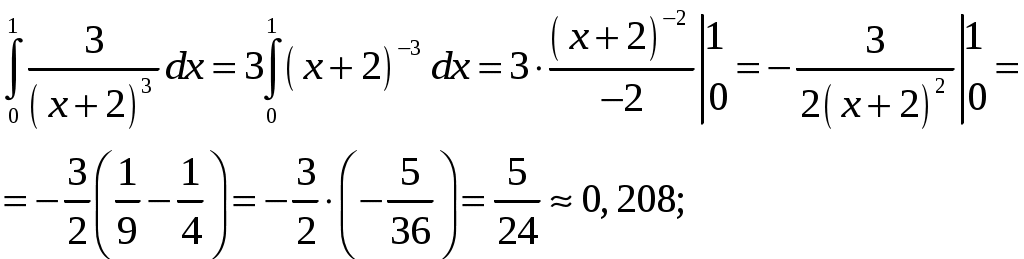 Разобьем интервал интегрирования на 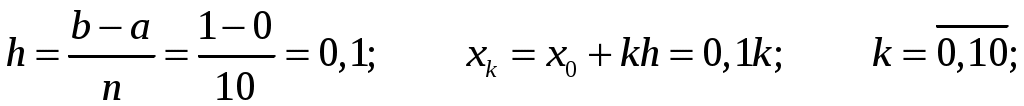 Вычисления проведем с четырьмя знаками после запятой и сведем в таблицу:
Применим формулу левых прямоугольников: Подставляя найденные значения, получим: 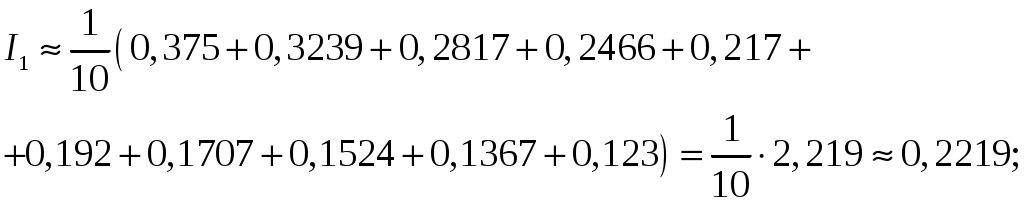 Применим формулу правых прямоугольников: Подставляя найденные значения, получим: 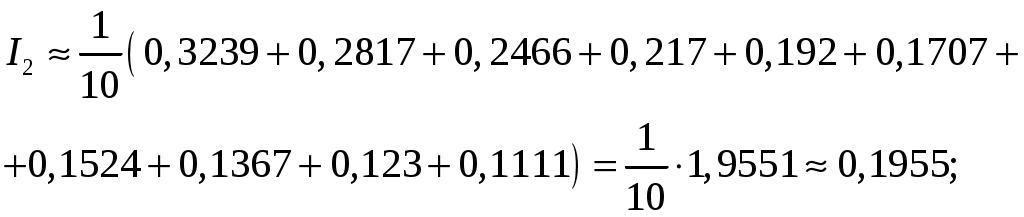 За окончательное значение интеграла 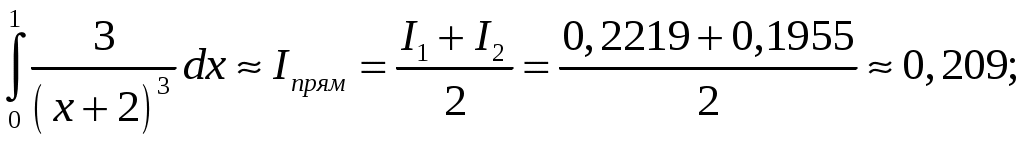 Найдем абсолютную погрешность вычислений: Получим: Найдем относительную погрешность вычислений: Получим: 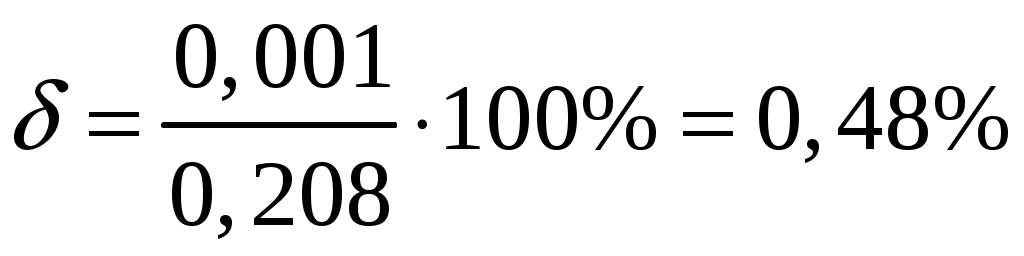 Вывод: значение интеграла, вычисленное по формуле прямоугольников, дает ошибку при вычислении, не превышающую 1%, т.е. является вполне приемлемым; для достижения лучшего результата следует увеличить число частей разбиения или использовать формулы трапеций или Симпсона. ЗАДАНИЕ 6. Определить, является ли функция Решение. Вычислим производную данной функции: Найденную производную и саму функцию подставим в исходное уравнение: 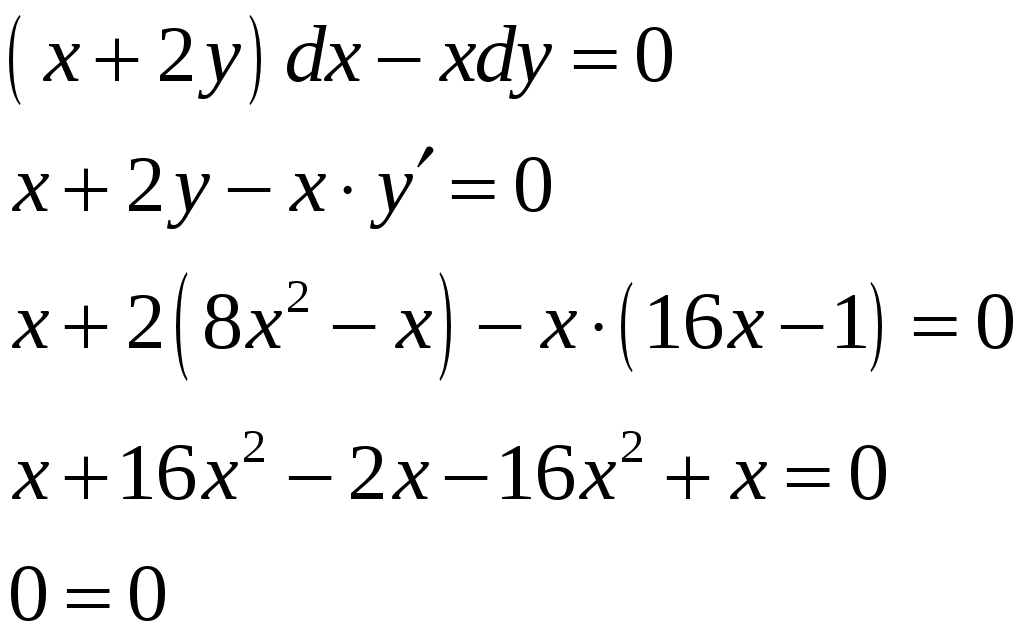 Получено верное равенство, следовательно, данная функция является решением данного дифференциального уравнения. ЗАДАНИЕ 7. Найти общее решение дифференциального уравнения. Найти частное решение по заданным начальным условиям. Используя полученное частное решение, построить интегральную кривую – линию Решение. Дано дифференциальное уравнение с разделяющимися переменными. Разделим переменные: 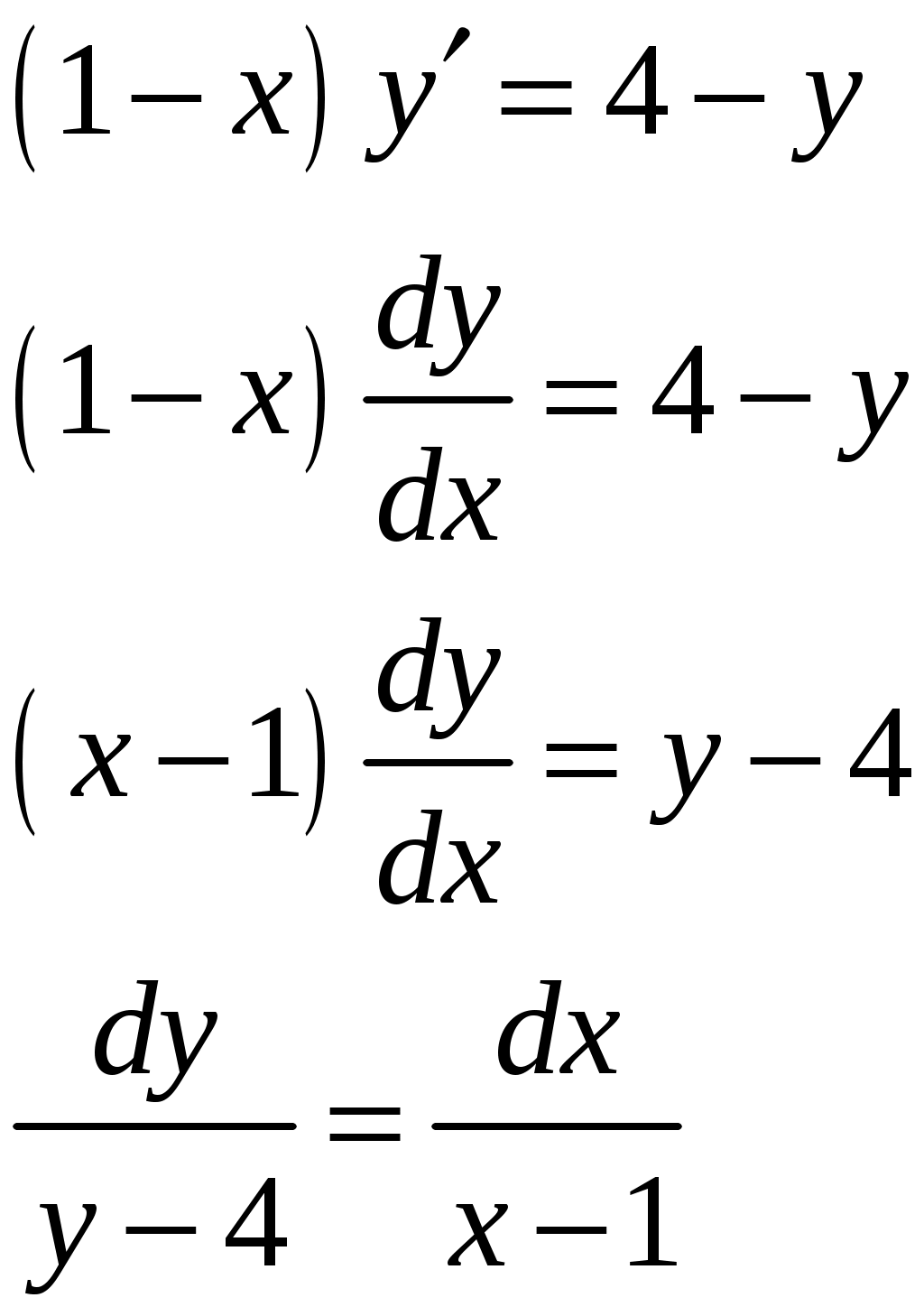 Проинтегрируем обе части: 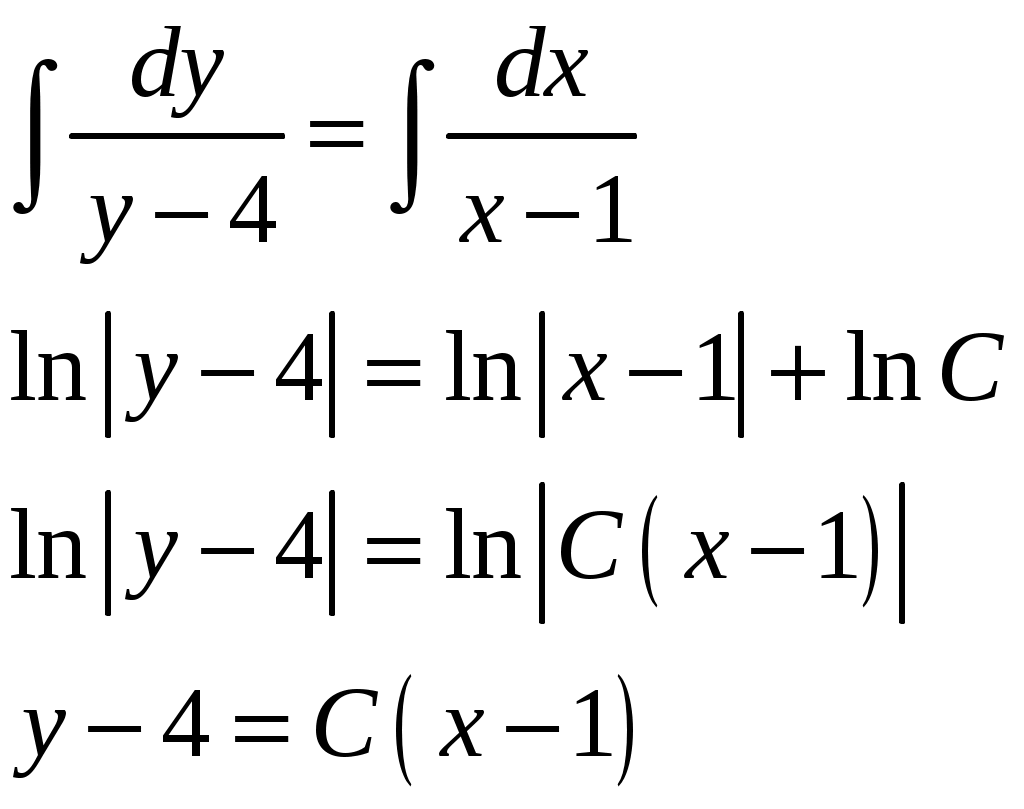 Тогда общее решение имеет вид: Общее решение Для частного решения найдем значение неопределенной константы, используя начальные условия 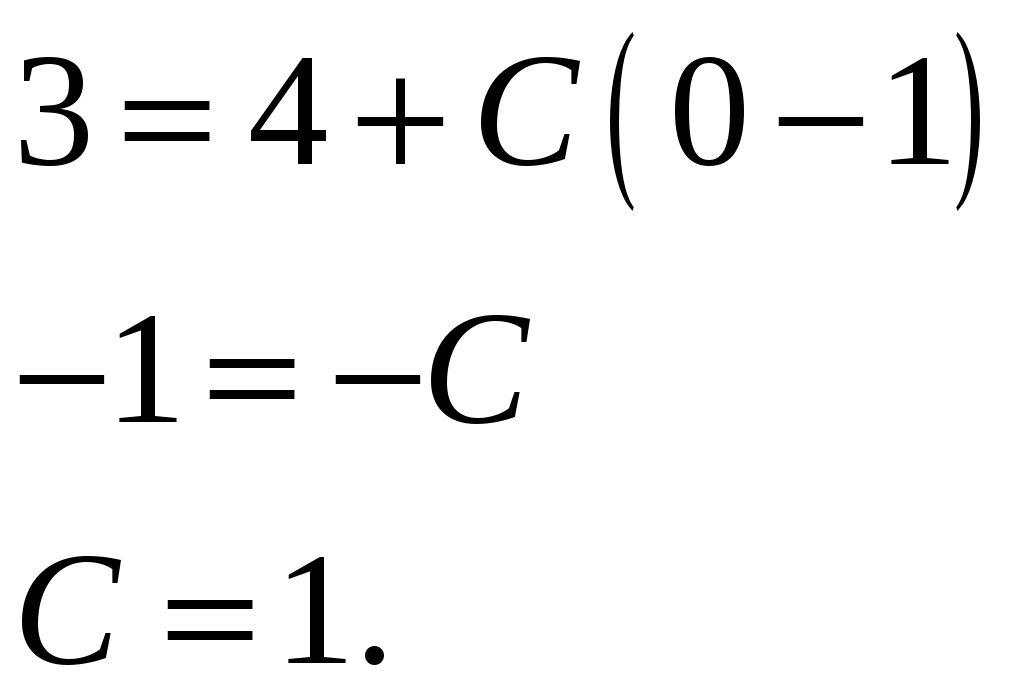 Подставив найденное значение: Тогда частное решение имеет вид: По полученным значениям координат точек построим интегральную кривую. 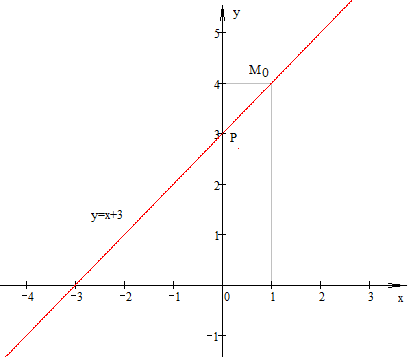 ЗАДАНИЕ 8. Найдите общее решение дифференциального уравнения первого порядка. 1) Решение. Уравнение имеет вид Решение будем искать в виде Подставив в уравнение, получим: 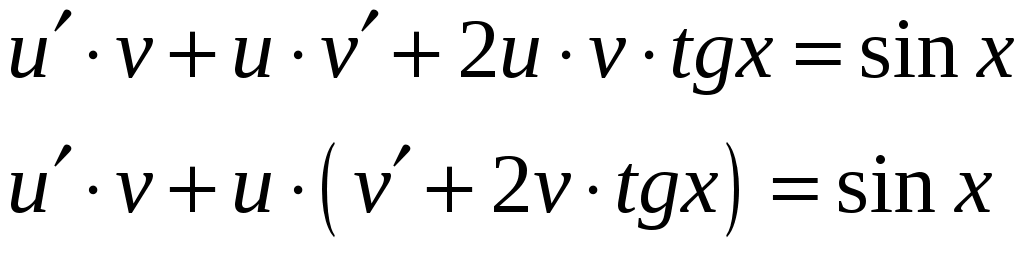 Пусть Получим систему уравнений с разделяющимися переменными: 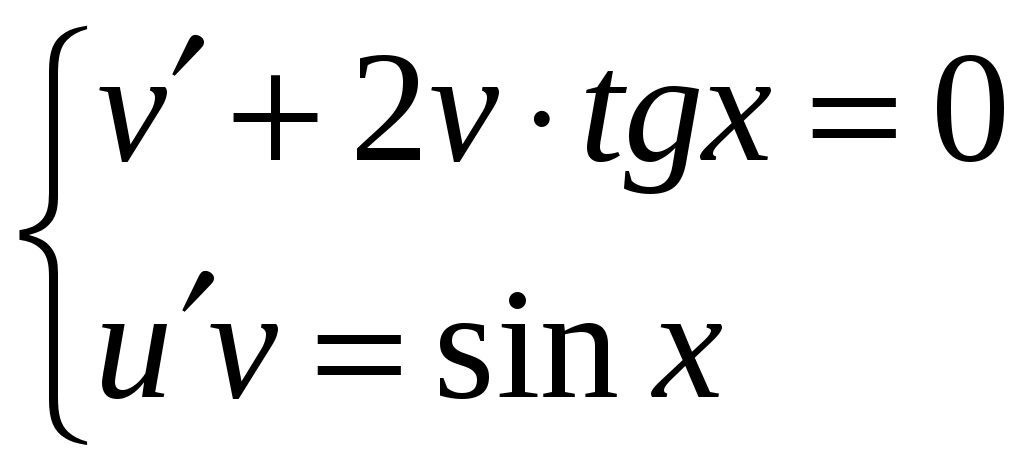 Решим систему. 1) 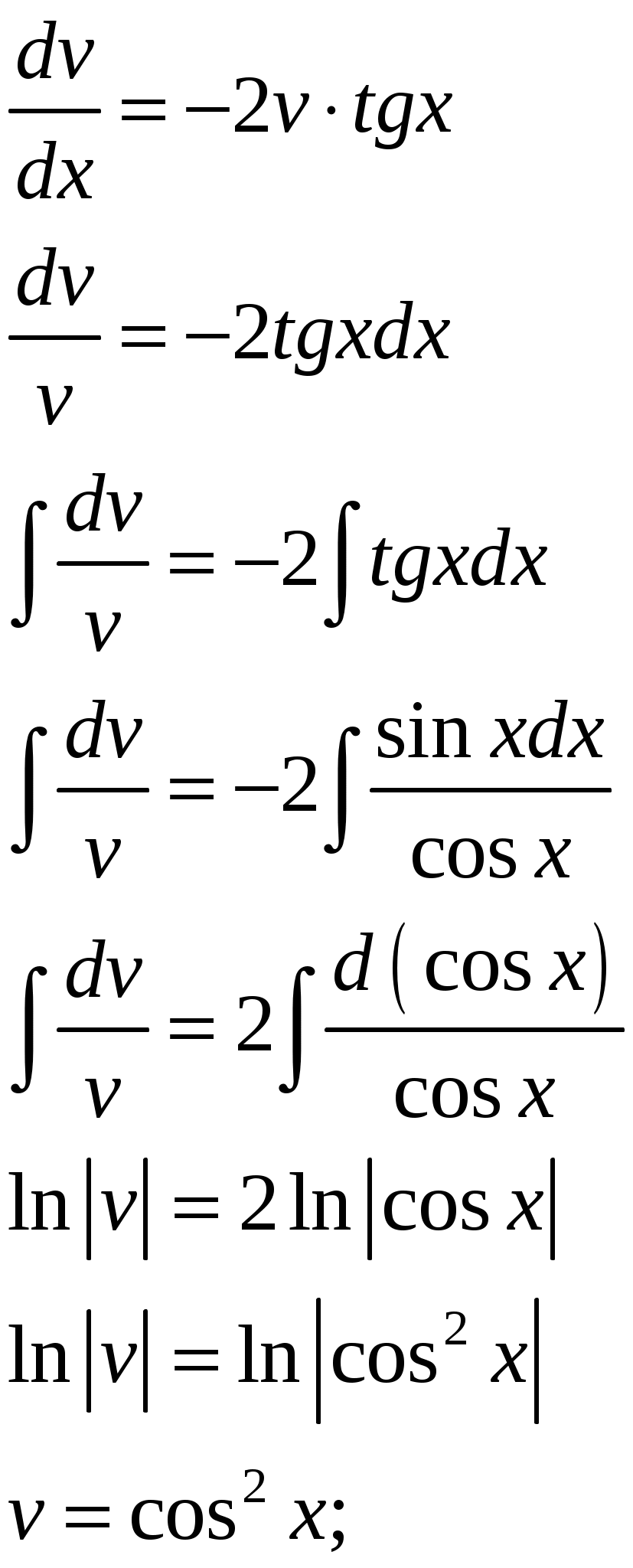 2) 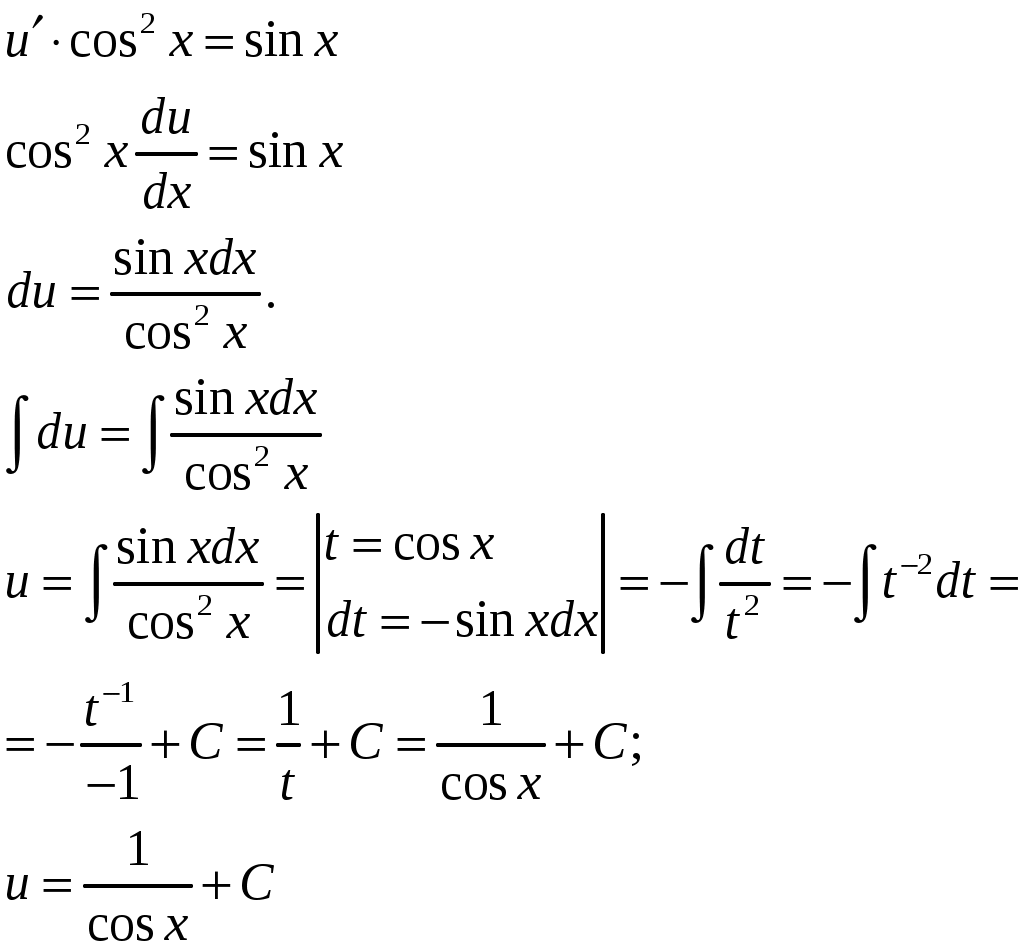 Тогда 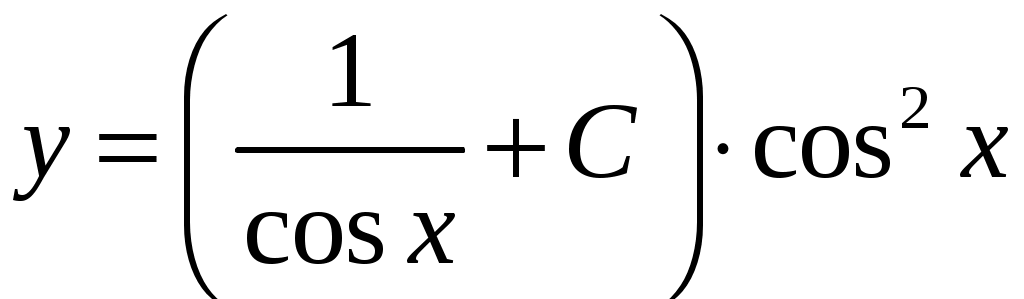 , откуда , откуда 2) 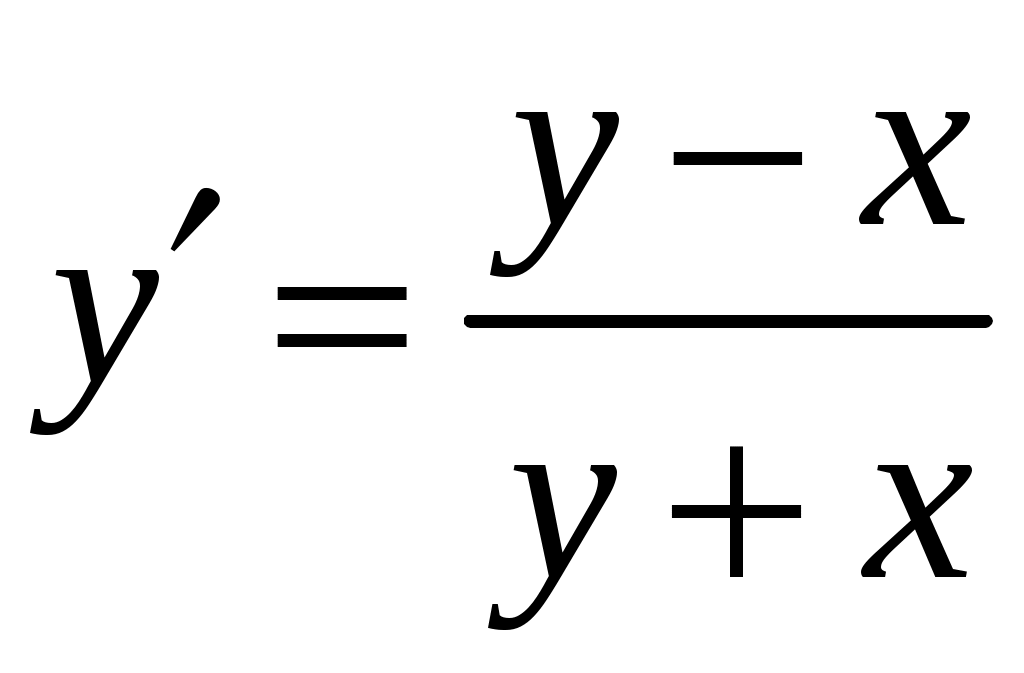 . .Решение. Приведем уравнение к стандартному виду. 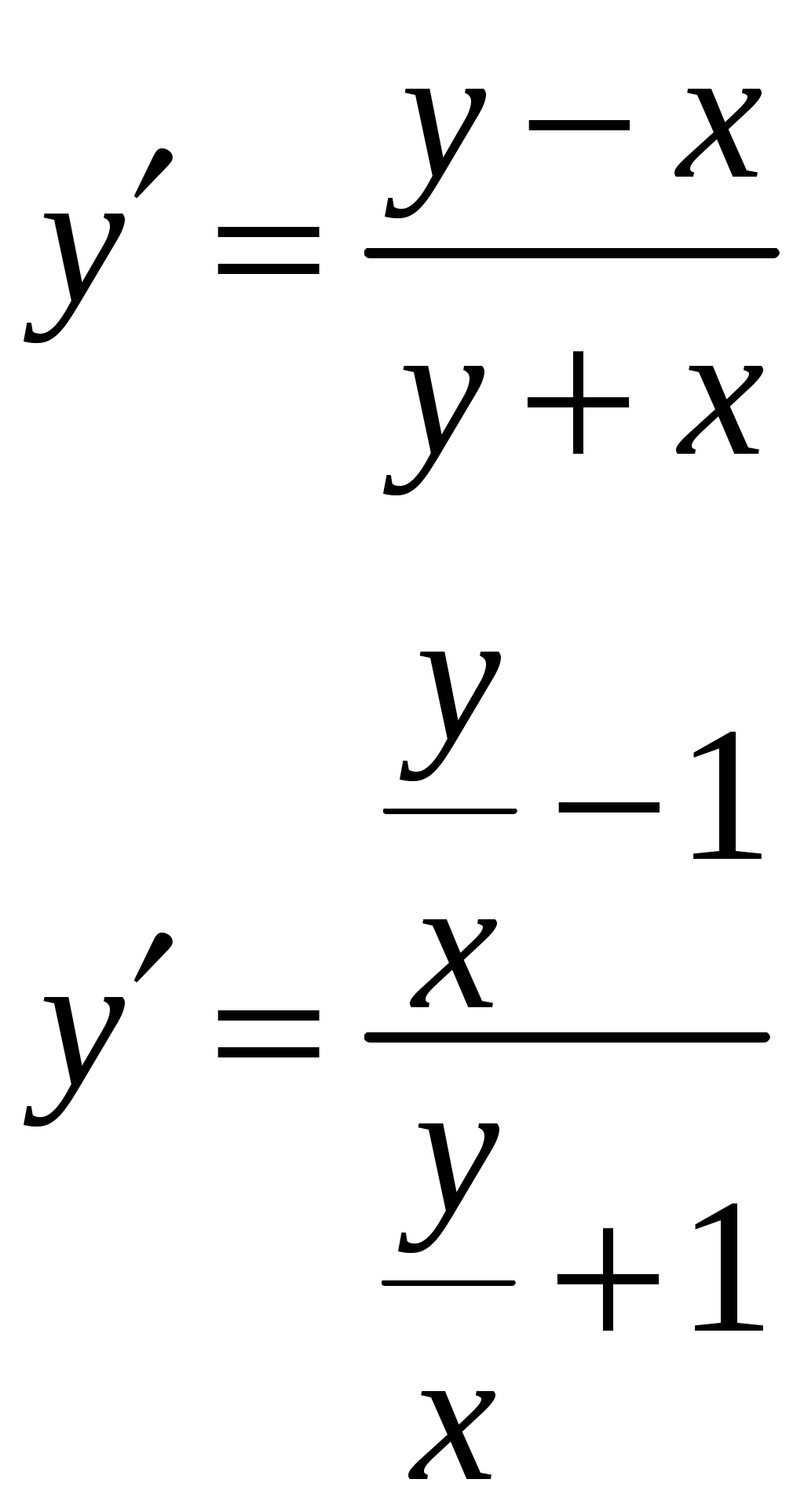 Общий вид уравнения определяется выражением 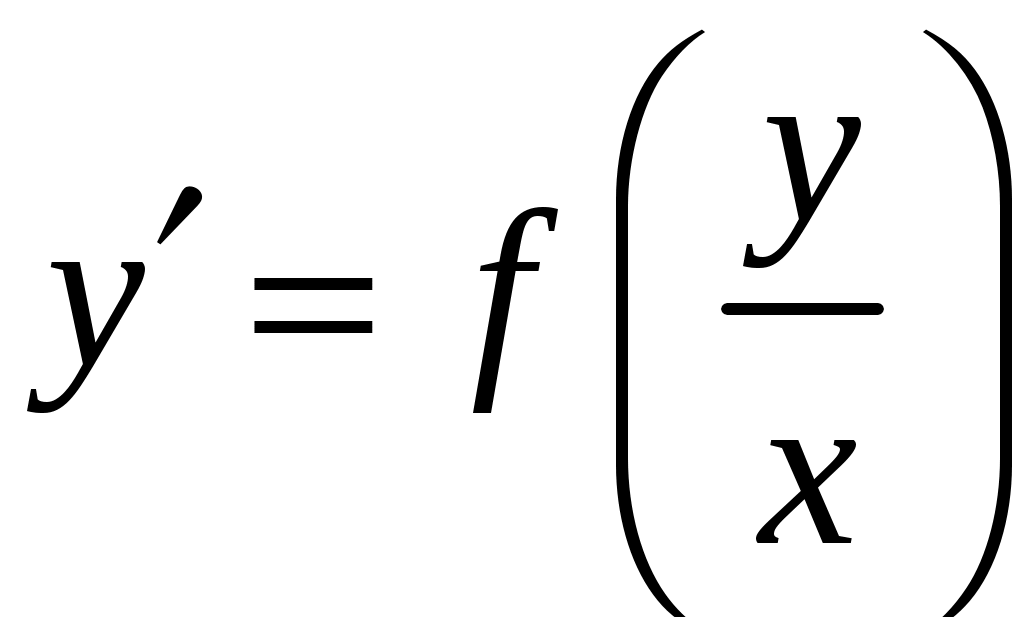 ‒ это однородное дифференциальное уравнение 1-го порядка. ‒ это однородное дифференциальное уравнение 1-го порядка. Пусть 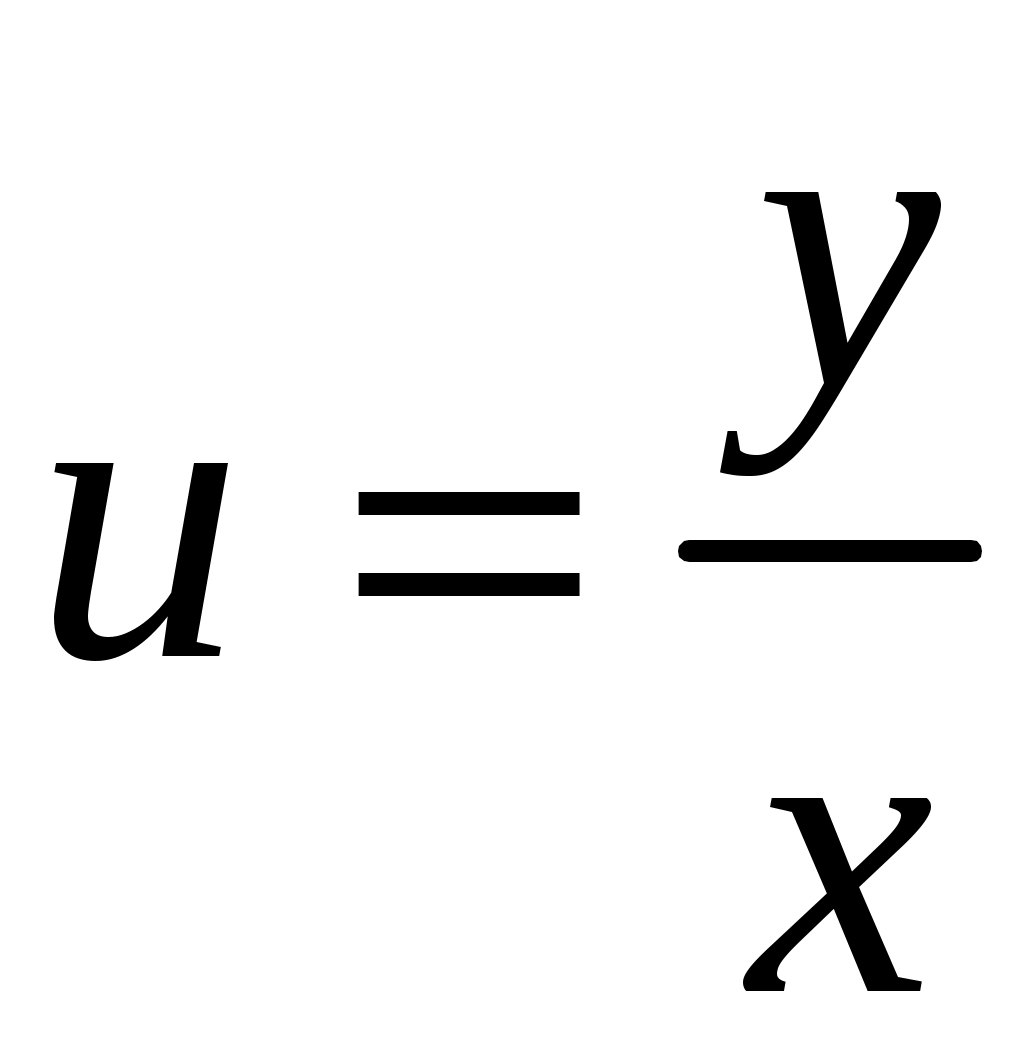 , тогда , тогда Подставляя в уравнение, получим: 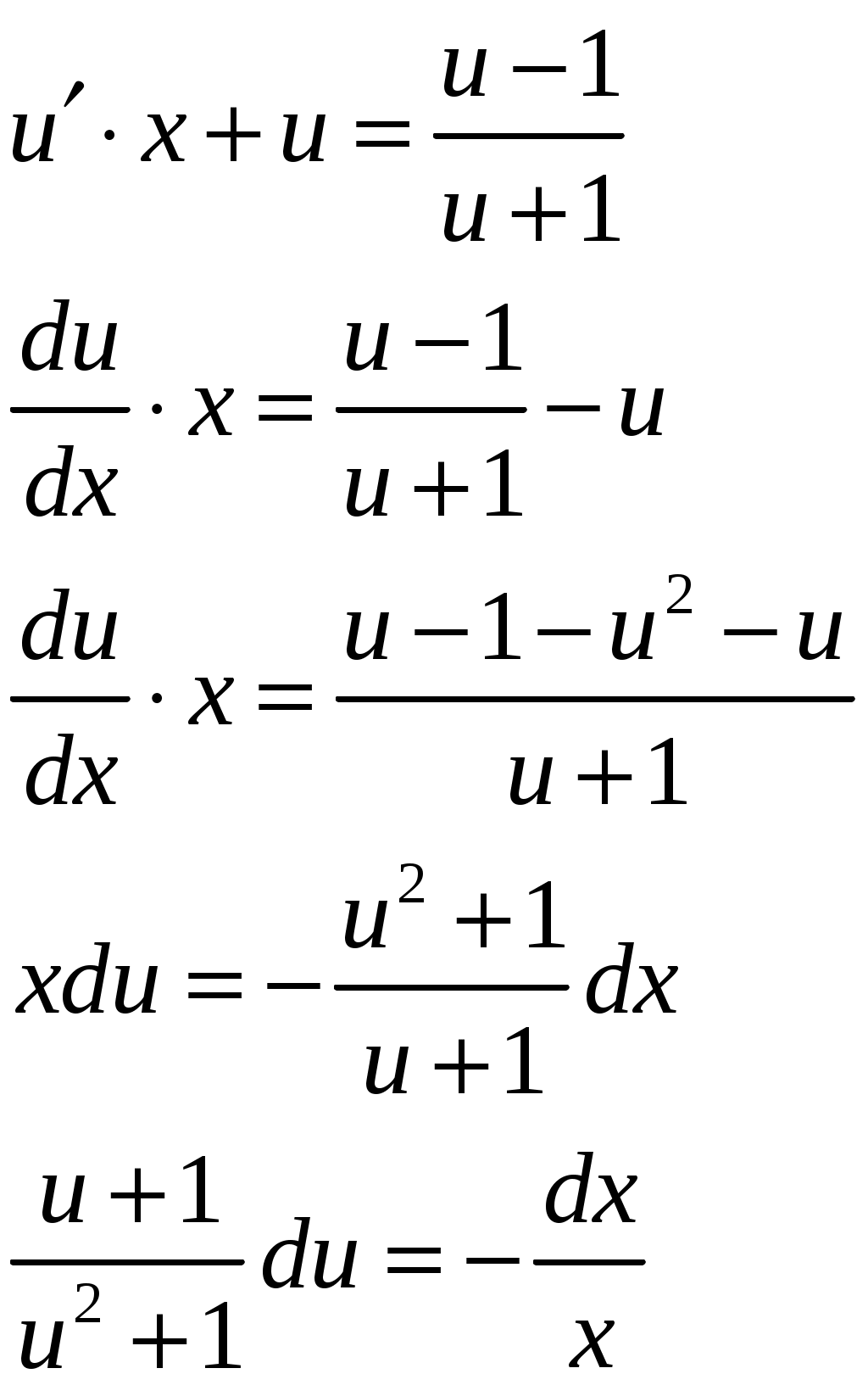 Проинтегрируем обе части: 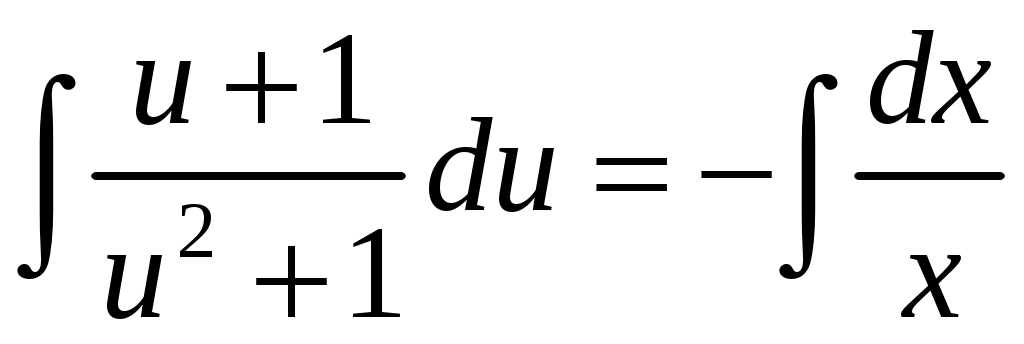 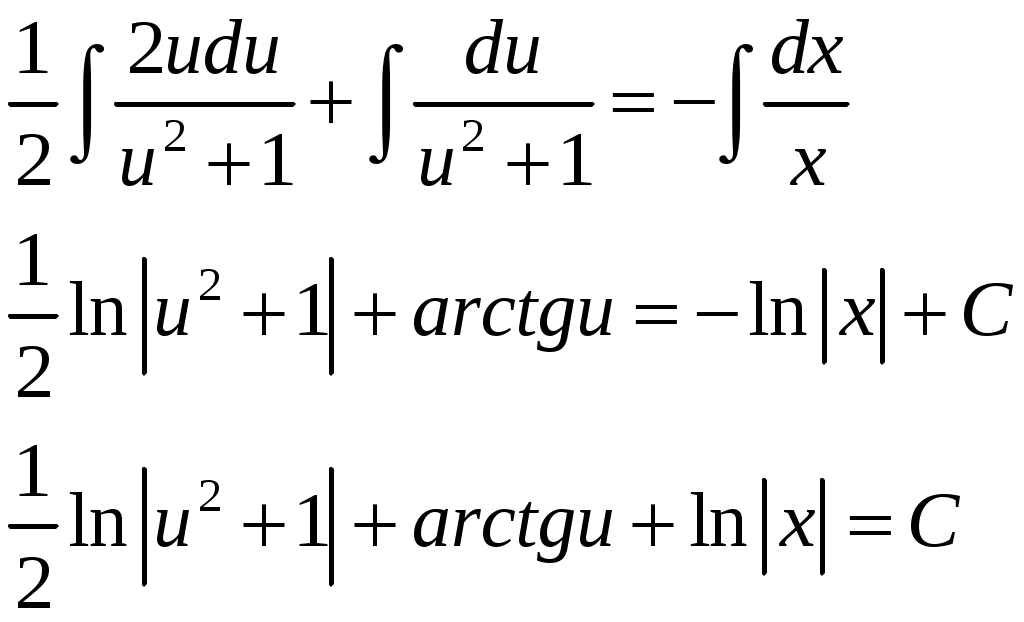 Так как 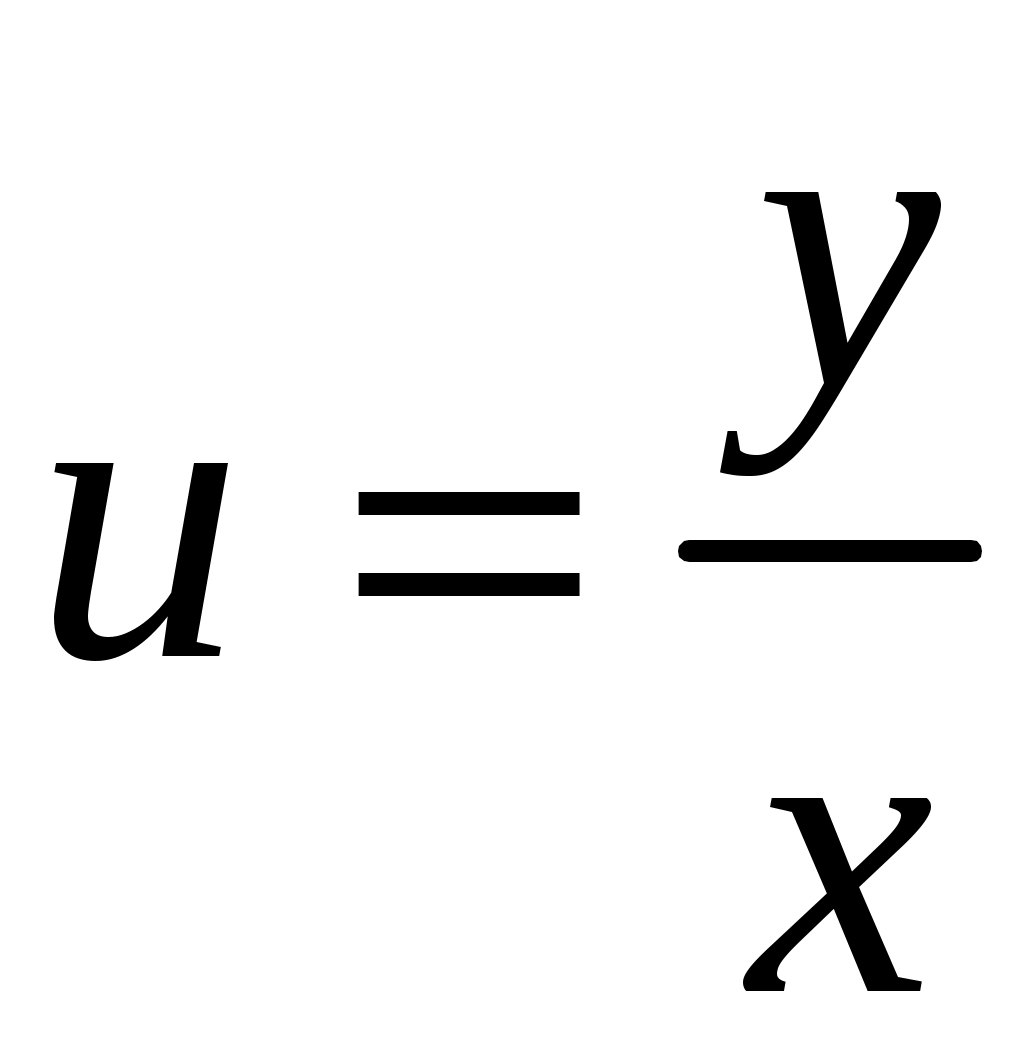 , то получим общий интеграл: , то получим общий интеграл: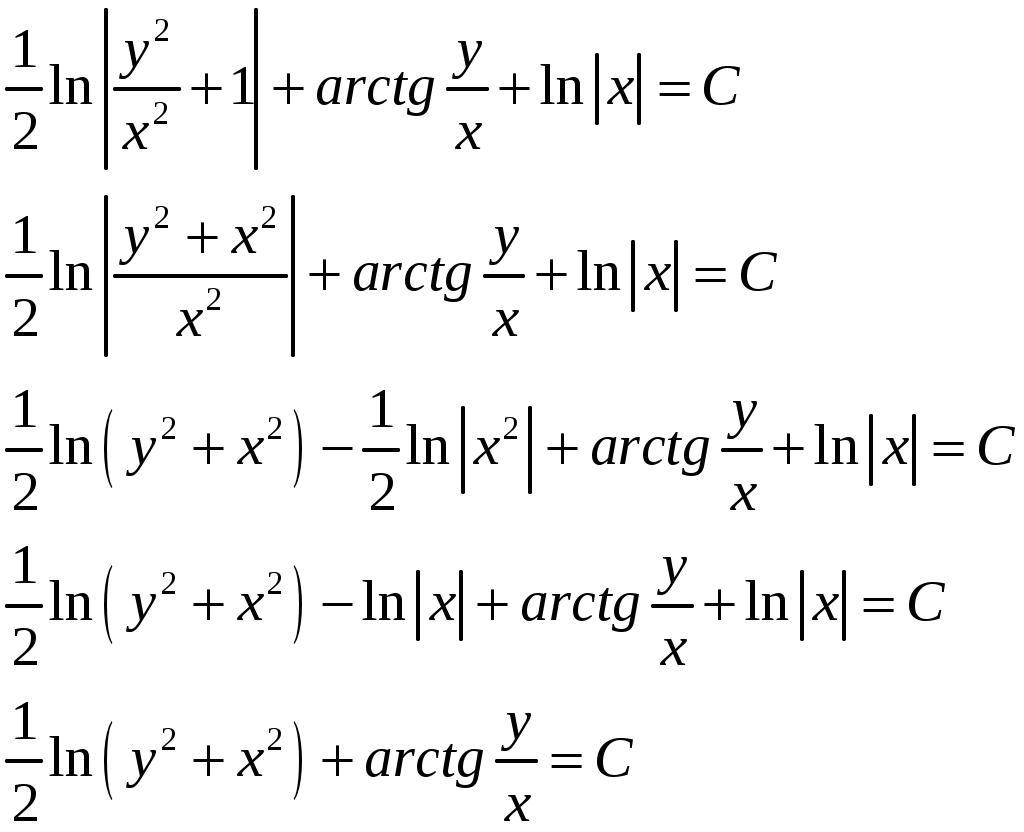 |