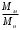Контрольная работа 2 Мишухин А. С. Вариант 7 Задача 1
 Скачать 338.34 Kb. Скачать 338.34 Kb.
|
|
Контрольная работа №2 Мишухин А. С. Вариант 7 Задача 1 Для трехфазного трансформатора, параметры которого приведены в табл. 1.1, определить коэффициент мощности холостого хода 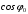 , коэффициент мощности , коэффициент мощности 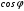 при нагрузках при нагрузках 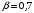 и и 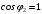 , , 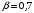 и и 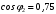 , сопротивления первичной и вторичной обмоток , сопротивления первичной и вторичной обмоток 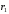 , , 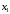 ; ; 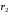 и и 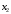 , расчетные сопротивления , расчетные сопротивления 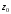 , , 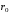 и и 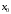 , угол магнитных потерь , угол магнитных потерь 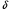 . Построить векторную диаграмму трансформатора для нагрузки . Построить векторную диаграмму трансформатора для нагрузки 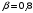 и и 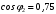 . Построить внешнюю характеристику . Построить внешнюю характеристику 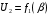 и зависимость к.п.д. от нагрузки и зависимость к.п.д. от нагрузки 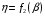 для для 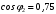 . Начертить Т-образную схему замещения трансформатора. . Начертить Т-образную схему замещения трансформатора.Табл. 1.1
Решение Определяем номинальный ток первичной обмотки: 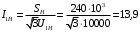 А. А.Определяем ток холостого хода и коэффициент мощности холостого хода: 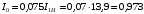 А. А.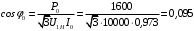 ; ; 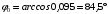 . .Определяем угол магнитных потерь: 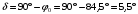 . .Определяем сопротивления обмоток: 1) Сопротивления короткого замыкания: 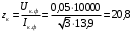 Ом; Ом;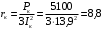 Ом; Ом;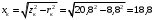 Ом. Ом.2) Сопротивления первичной обмотки: 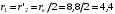 Ом; Ом;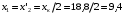 Ом. Ом.3) Сопротивления вторичной обмотки: 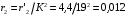 Ом; Ом;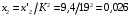 Ом. Ом.Сопротивления намагничивающей цепи: 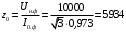 Ом; Ом;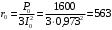 Ом; Ом;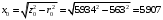 Ом. Ом.Для построения внешней характеристики  определяем потерю напряжения во вторичной обмотке трансформатора: определяем потерю напряжения во вторичной обмотке трансформатора: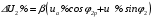 , ,где uа%, uр% - соответственно активное и реактивное падение напряжений; 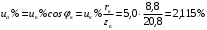 ; ;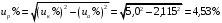 . .Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле 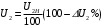 . .Задаваясь различными значениями β, определяем напряжение U2 (табл. 1.2). Для построения зависимости 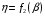 расчет коэффициента полезного действия производим по формуле расчет коэффициента полезного действия производим по формуле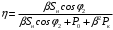 . .Результаты вносим в табл. 1.2. Таблица 1.2
Полученные характеристики показаны на рис. 1.1. 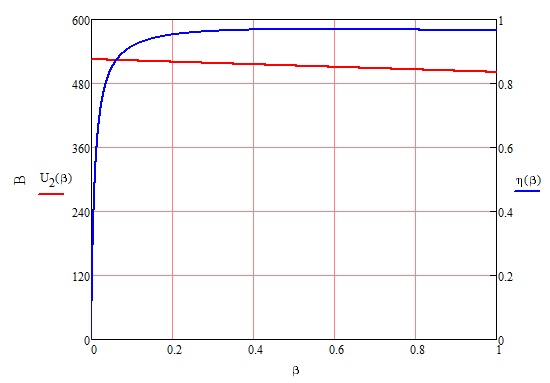 Рис. 1.1 Определим нагрузку, при которой трансформатор имеет максимальный КПД: 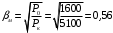 ; ; 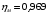 . .Построение векторной диаграммы начнем с вектора фазного напряжения 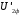 , величина которого для , величина которого для 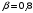 и и 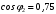 будет равна: будет равна: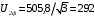 В. В.Приведенное значение вторичного напряжения: 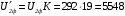 В. В. Рис. 1.2 Вектор тока 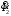 отстает по фазе от вектора отстает по фазе от вектора 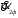 на заданный угол на заданный угол 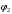 и равен: и равен: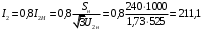 А. А.Падения напряжения во вторичной обмотке: 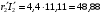 В; В;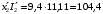 В. В.Электродвижущую силу 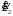 находим из уравнения электрического состояния, составленного по второму закону Кирхгофа, для вторичной цепи: находим из уравнения электрического состояния, составленного по второму закону Кирхгофа, для вторичной цепи: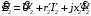 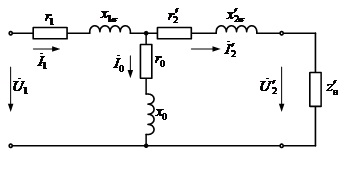 Рис. 1.3 Вектор тока 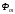 отстает от вектора отстает от вектора 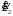 на на 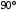 ; а ток холостого хода ; а ток холостого хода 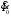 опережает поток опережает поток 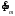 на угол потерь на угол потерь 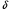 . .Ток в первичной обмотке трансформатора 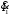 получаем из уравнения намагничивающих магнитодвижущих сил: получаем из уравнения намагничивающих магнитодвижущих сил: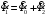 , где , где 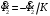 . .Вектор напряжения первичной обмотки трансформатора 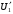 определяем из уравнения электрического состояния, составленного по второму закону Кирхгофа для первичной цепи: определяем из уравнения электрического состояния, составленного по второму закону Кирхгофа для первичной цепи: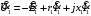 . .Падения напряжения на первичной обмотке: 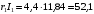 В. В.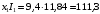 В. В.Векторная диаграмма трансформатора приведена на рис. 1.2. Т-образная схема замещения трансформатора изображена на рис. 1.3. Задача 2 Двигатель параллельного возбуждения, номинальное напряжение которого 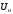 при номинальной нагрузке потребляет ток при номинальной нагрузке потребляет ток 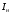 , а при холостом ходе — , а при холостом ходе — 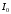 Номинальная скорость вращения Номинальная скорость вращения 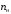 , сопротивление обмотки якоря , сопротивление обмотки якоря 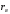 , сопротивление цепи возбуждения , сопротивление цепи возбуждения 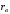 . Магнитные и механические потери принять постоянными при всех режимах работы двигателя (табл. 2.1). Определить: номинальную мощность двигателя . Магнитные и механические потери принять постоянными при всех режимах работы двигателя (табл. 2.1). Определить: номинальную мощность двигателя 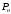 , номинальный вращающий момент , номинальный вращающий момент 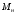 , номинальный к.п.д. , номинальный к.п.д. 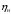 , ток , ток 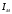 , при котором мощность на валу двигателя достигнет максимального значения, величину этой мощности , при котором мощность на валу двигателя достигнет максимального значения, величину этой мощности 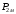 и к.п.д. и к.п.д. 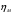 . .Таблица 2.1
Решение Номинальная мощность на валу двигателя 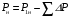 , ,где 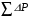 - суммарные потери в двигателе; - суммарные потери в двигателе; 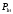 - потребляемая мощность. - потребляемая мощность.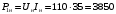 Вт. Вт.Для определения потерь в цепи якоря и цепи возбуждения надо знать ток в цепи якоря 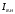 и ток возбуждения и ток возбуждения 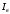 : :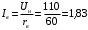 А; А;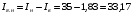 А. А.Потери в обмотке якоря и в цепи возбуждения: 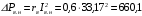 Вт; Вт;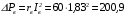 Вт. Вт.Магнитные и механические потери: 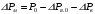 , ,где 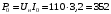 Вт; Вт; 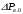 - потребляемая мощность при холостом ходе двигателя: - потребляемая мощность при холостом ходе двигателя: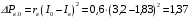 Вт; Вт;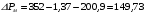 Вт; Вт;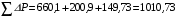 Вт; Вт;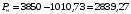 Вт. Вт.Номинальный к.п.д.: 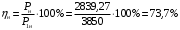 . .Номинальный вращающий момент: 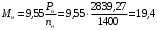 Нм. Нм.Для определения тока, при котором мощность на валу двигателя достигает максимального значения, находим первую производную 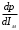 выражения выражения 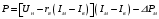 и, приравняв ее к нулю, определяем и, приравняв ее к нулю, определяем 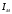 : :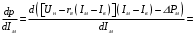 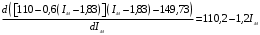 ; ;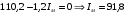 А. А.Потребляемая мощность: 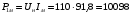 Вт. Вт.Ток в цепи якоря и потери в обмотке якоря: 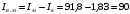 А; А;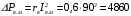 Вт. Вт.Суммарные потери и мощность на валу: 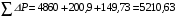 Вт; Вт;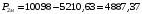 Вт. Вт.КПД при максимальной мощности на валу: 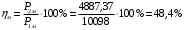 . .Задача 3 Трехфазный асинхронный двигатель с фазным ротором, обмотки статора и ротора которого соединены звездой, включен в сеть под номинальное напряжение 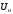 с частотой с частотой 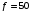 Гц. Гц.Определить: номинальный ток статора 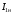 , номинальный , номинальный 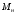 и максимальный и максимальный 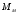 моменты, сопротивления моменты, сопротивления 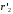 , , 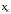 , , 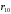 и и 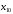 в Г-образной схеме замещения (рис. 3.1), приведенный ток ротора в Г-образной схеме замещения (рис. 3.1), приведенный ток ротора 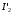 , ток в статоре в режиме холостого хода , ток в статоре в режиме холостого хода 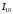 и коэффициент мощности и коэффициент мощности 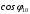 . Данные для расчета приведены в табл. 3.1. . Данные для расчета приведены в табл. 3.1.Таблица 3.1
Решение Г-образная схема замещения асинхронного электродвигателя с фазным ротором показана на рис. 3.1. 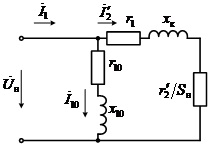 Рис. 3.1 Номинальный ток статора: 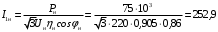 А. А.Для определения реактивного сопротивления воспользуемся формулой максимального электромагнитного момента: 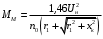 , ,из которой следует, что 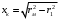 , ,где 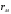 - расчетное сопротивление: - расчетное сопротивление: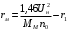 . .Приведенное активное сопротивление ротора 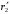 найдем из формулы, выражающей зависимость номинального электромагнитного момента найдем из формулы, выражающей зависимость номинального электромагнитного момента 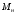 от номинального скольжения от номинального скольжения 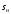 : :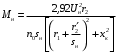 , ,из которой следует, что 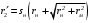 , ,где 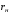 - расчетное сопротивление: - расчетное сопротивление: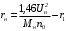 . .По каталожным данным номинальный и максимальный моменты: 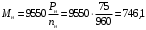 Нм; Нм;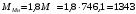 Нм. Нм.Расчетные сопротивления: 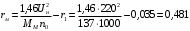 Ом; Ом;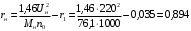 Ом, Ом,где 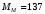 кгм; кгм; 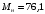 кгм. кгм.Реактивное сопротивление: 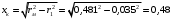 Ом. Ом.Приведенное активное сопротивление ротора: 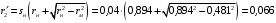 Ом. Ом.Определяем приведенный ток 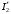 при номинальном режиме работы двигателя: при номинальном режиме работы двигателя: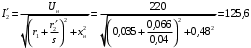 А. А.Для Г – образной схемы замещения (см. рис. 3.1) составим два уравнения баланса активных и реактивных мощностей при номинальном режиме работы двигателя: 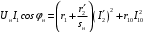 ; ;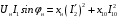 . .Активная мощность двигателя в режиме холостого хода, отнесенная к одной фазе обмотки статора: 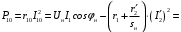 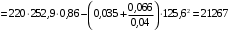 Вт. Вт.Реактивная мощность двигателя в режиме холостого хода, отнесенная к одной фазе обмотки статора: 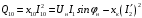 . .Величина 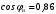 соответствует соответствует 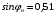 , поэтому , поэтому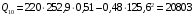 ВАр. ВАр.Полная мощность двигателя в режиме холостого хода, отнесенная к одной фазе обмотки статора: 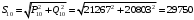 ВА. ВА.Ток холостого хода: 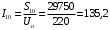 А. А.Коэффициент мощности при холостом ходе двигателя 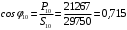 . .Сопротивления при холостом ходе: 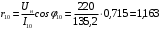 Ом; Ом;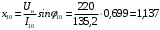 Ом. Ом. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||