Расчет установившегося режима ЭЭС на основе линейных математических моделей.. Практическая работа №4 Тема - Расчет установившегося режима ЭЭС. Расчет установившегося режима ээс на

• Название: Расчет установившегося режима ээс на
• Анкор: Расчет установившегося режима ЭЭС на основе линейных математических моделей
• Дата: 11.04.2022
• Размер: 63.04 Kb.
• Имя файла: Практическая работа №4 Тема - Расчет установившегося режима ЭЭС .docx
• Тип: Задача; #461200

Практическая работа №4

РАСЧЕТ УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЭС НА ОСНОВЕ ЛИНЕЙНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Цельработы. Моделирование установившихся режимов ЭЭС на основе линейных уравнений состояния (обобщенного уравнения состояния и уравнения узловых напряжений) в среде Mathcad.

Краткие теоретические сведения

Задача расчета и анализа установившихся режимов является базовой как при проектировании, так и управлении электроэнергетическими системами (ЭЭС).

При проектировании ЭЭС расчет установившихся режимов производится с целью выбора и уточнения параметров проектируемой системы. В процессе эксплуатации подобные расчеты позволяют оперативно управлять и прогнозировать работу ЭЭС. При этом осуществляется оценка допустимости режима по техническим условиям оборудования.

Постановка задачи расчета режима функционирования определяется особенностями ЭЭС как сложной технической системы, которая включает в себя большое количество элементов, вырабатывающих, преобразующих, передающих, распределяющих, потребляющих электроэнергию и образующих сложно-замкнутую разветвленную структуру.

Режимомработы ЭЭС называется состояниесистемы в любой момент времени или на некотором интервале времени.

Под установившимсярежимомпонимается такое состояние ЭЭС, когда параметры системы на рассматриваемом интервале времени сохраняются неизменными или изменяются достаточно медленно. Задача расчета установившихся режимов ЭЭС сводится к определению совокупности параметров, характеризующих работу системы: напряжений в различных точках системы, токов в ее элементах, потоков и потерь мощности и т.д.

Проведение расчета установившегося режима связано с рядом основных этапов:

• 
  предварительное преобразование и переход к расчетной схеме электрической системы;
  
• 
  формирование уравнения состояния по известным исходным данным с учетом структуры расчетной схемы;
  
• 
  выбор метода расчета, составление алгоритма и программы на ЭВМ;
  
• 
  проведение расчета установившегося режима на ЭВМ;
  
• 
  анализ точности полученных результатов.
  

В основе решения задачи расчета режима лежит использование математических моделей макроуровня, представляющих собой линейные уравнения состояния (например, обобщенное уравнение состояния, уравнения узловых напряжений) и нелинейные уравнения состояния (например, уравнения узловых напряжений в форме баланса мощности или в форме баланса токов).

Математические модели макроуровня, применяемые в задаче расчета установившихся режимов, основаны на законах Ома и Кирхгофа, представленных в матричной форме записи.

Рассмотрим две формы линейных уравнений состояния, которые позволяют произвести расчет установившегося режима при упрощенном представлении нагрузки и генерации мощности с помощью линейных источников тока (задающего тока).

Модель 1. Классической формой линейной модели является обобщенноеуравнениесостояния.

1. 
   й закон Кирхгофа: M·I_B = J; (4.1)
   
2. 
   й закон Кирхгофа: N·Z_B·I_B = E_K, (4.2)
   

где М– матрица инциденций 1-го рода описывает связь ветвей и узлов схемы.

j
Структура Правила формирования

В е т в и

j

У

¹, если ветвь выходит из узла i_

i

М = <sup>З


m</sup>ij

m_ij

–1, если ветвь входит в узел i _ ^j

^{Л 0}, если ветвь не связана с узлом

ы
N– матрица инциденций 2-го рода описывает связь ветвей и независимых контуров

Структура Правила формирования

н
к о

N= _т ⁱ

у р ы

_jВ е т в и








ⁿij






n_ij

^1, если направление ветви и ^j

контура совпадает

i

–1, если направление ветви и ^j

контура не совпадает

^0, если ветвь не связана с контуром ⁱ

n число узлов, m числоветвей, L числонезависимых контуров _.

Вектор задающих токов Матрица сопротивлений ветвей

Вектор токов ветвей Вектор ЭДС ветвей Вектор контурных токов

Обобщенное уравнение состояния, полученное на основе 1-го и 2-го законов Кирхгофа, имеет вид:

A·I_B= F, (4.3)
где – блочная матрица коэффициентов; – блочная матрица свободных членов уравнений.
Примечание: деление заменяется на умножение обратной матрицы. Обратную матрицу можно найти по следующей формуле: (K)^-1=(1/|K|)·K^T, где K=N·Z_B; |K| – определитель матрицы, K^T

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы. Транспонированнаяматрица– это матрица, полученная из исходной путем замены строк на столбцы. Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Представленная модель является универсальной, но не экономичной в связи с большой размерностью системы уравнений (4.3). Поэтому наибольшее распространение в практике расчета установившихся режимов получило уравнение узловых напряжений.
Модель2. Линейная форма уравненияузловыхнапряжений.

Y_у·U_Δ=J-M·Y_B·E_B, (4.4)

где Y_у= M·Y_B·M^T– матрица узловых проводимостей; U_Δ=[U_i-U_Б] – матрица узловых

B
напряжений; U_Б– базисное напряжение балансирующего узла; Y_B=Z^1

– матрица

проводимостей ветвей; E_B– матрица ЭДС ветвей; J– вектор задающих токов.

Если в схеме замещения нагрузка и генерация мощности моделируются с помощью задающих токов, то E_B= 0 и уравнение узловых напряжений имеет вид

Y_у·U_Δ=J. (4.5)

Алгоритм расчета установившегося режима по уравнению узловых напряжений включает в себя следующие этапы .

1. 
   Расчет узловых напряжений по уравнению (4.5)
   

у
U_Δ=Y^1 ·J.

2. 
   Определение уровней напряжений в узлах U= U_Δ + U_Б. (4.6) Возможно выполнение этапов 1 и 2 одновременно.
   

у
U= Y^1 (J- Y_БU_Б), (4.7)

Y_Б – матрица проводимостей ветвей, связывающих узлы схемы с балансирующим узлом Б.

3. 
   Расчет падений напряжений в ветвях схемы
   

U_B=M^TU_Δ=M^T(U-U_Б). (4.8)

4. 
   Определение токов в ветвях схемы
   

I_B=Y_B(U_B+ E_B). (4.9)

5. 
   Расчет потоков мощности Р,Q.
   

Задание на лабораторную работу

1. 
   Расчет установившегося режима по линейным моделям для сети постоянного тока.
   

1. 
   Рассчитать токи в ветвях расчетной схемы сети постоянного тока (рис. 4.1), используя обобщенное уравнение состояния. Исходные данные по вариантам приведены в табл. 4.3. Вариант определяется по последней цифре в номере зачетной.
   

Алгоритмрасчета

 Ввести исходные данные M, N, вектор-столбец сопротивлений ветвей Z, вектор задающих токов нагрузки Jвектор ЭДС ветвей Е_В.

 Сформировать диагональную матрицу сопротивлений Z_B, используя

встроенную функцию Z_B= diag(Z): Z_B  diag(Z) .

 Рассчитать промежуточную матрицу K= N·Z_B, матрицу контурных ЭДС

Е_К.

 Сформировать блочные матрицы коэффициентов Aи свободных членов уравнения F, используя встроенную функцию stack, например:

A:=stack(M, K).

 Рассчитать токи в ветвях схемы по обобщенному уравнению состояния через обратную матрицу коэффициентов.




Рисунок 4.1

Таблица 4.1

№	Сопротивления ветвей, Ом
	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10	Z11
1	0.2	0.3	0.4	0.5	0.7	0.8	0.2	0.4	0.7	0.9	0.1
2	0.3	0.2	0.5	0.6	0.7	0.8	0.2	0.4	0.6	0.9	0.1
3	0.3	0.4	0.8	0.9	0.5	0.7	0.6	0.3	0.7	0.2	0.1
4	0.2	0.5	0.7	0.9	0.6	0.4	0.3	0.6	0.9	0.3	0.8
5	0.2	0.4	0.3	0.5	0.3	0.6	0.4	0.5	0.8	0.2	0.7
6	0.5	0.3	0.6	0.9	0.7	0.8	0.5	0.4	0.6	0.4	0.2
7	0.2	0.3	0.4	0.8	0.3	0.5	0.8	0.5	0.6	0.9	0.2
8	0.3	0.5	0.4	0.5	0.6	0.9	0.8	0.5	0.7	0.8	0.7
9	0.1	0.5	0.3	0.5	0.4	0.1	0.2	0.3	0.7	0.6	0.1
10	0.2	0.3	0.5	0.6	0.8	0.2	0.3	0.4	0.9	0.6	0.7

Таблица 4.1 (продолжение)

Задающие токи, кА								δ, рад
J1	J2	J3	J4	J5	J6	J7	J8
3	4	6	8	9	11	6	9	π/3
3	5	6	7	9	11	5	9	π/4
2	3	5	8	6	3	7	1	π/6
3	2	5	7	3	4	7	6	π/3
2	3	6	8	4	9	6	1	π/6
3	5	4	8	6	5	9	6	π/4
8	3	4	6	5	9	7	2	π/6
3	8	6	4	9	10	6	8	π/3
2	4	3	5	6	9	7	10	π/4
3	5	4	5	6	8	9	4	π/6

U_б  10,5 кВ, S_б  7 МВА,

E_q 1.07, U_c 1,

P_d 60, T_j 14 c,

x_d 1.7, x_d^

 0.172, T_d0  7.26.

2. 
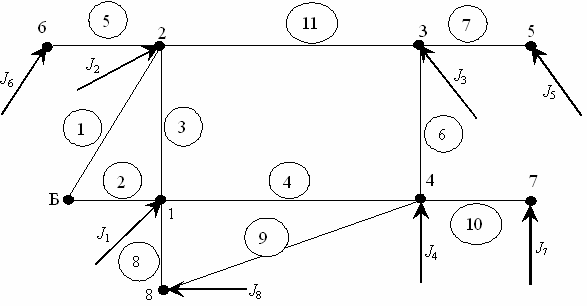
   Определить параметры установившегося режима для расчетной схемы, по уравнению узловых напряжений в линейной форме.
   

Алгоритмрасчета

 Рассчитать матрицу узловых проводимостей по Y_у= M·Y_B·M^T.

 Определить уровни напряжений в узлах по (4.7), либо используя (4.5) и (4.6); ^U_б ^{ 10,5 кB} .

 Рассчитать падения напряжений в ветвях схемы по (4.8).

 Определить токи в ветвях схемы по (4.9).

3. 
   Сравнить результаты расчета – токи в ветвях схемы, полученные по
   

Модели 1 и Модели 2.

2. 
   Расчет установившегося режима по линейным моделям для сети переменного тока.
   
   1. 
      Определить параметры установившегося режима для расчетной схемы по уравнению узловых напряжений в линейной форме. Исходные данные по вариантам приведены в табл. 4.1. Расчет провести с учетом единиц измерения параметров.
      

Алгоритмрасчета

 Ввести исходные данные М, вектор-столбец сопротивлений ветвей Z(Ом),

вектор задающих токов нагрузки J(кА),

^U_б ^{ 10,5 кB} .

 Сформировать диагональную матрицу проводимостей ветвей в сименсах

^YBi,i

_1

Z_i

, где ^{i: 1…7} .

 Сформировать матрицу проводимостей ветвей, связывающих узлы схемы с балансирующим Y_Б в сименсах.

 Рассчитать матрицу узловых проводимостей в сименсах.

 Рассчитать напряжения в узлах схемы в киловольтах.

 Определить модуль и фазу напряжений в киловольтах и градусах.

 Рассчитать вектор падений напряжения в ветвях схемы в киловольтах.

 Рассчитать токи в ветвях схемы в килоамперах.

3. 
   Осуществить проверку результатов по балансу токов: сумма задающих токов должна быть равна току балансирующего узла с обратным знаком. Ток балансирующего узла равен алгебраической сумме токов ветвей, связанных с узлом Б с учетом их направления.