банка. Ответы, решения и разбалловки
 Скачать 159.27 Kb. Скачать 159.27 Kb.
|
|
ОТВЕТЫ, РЕШЕНИЯ И РАЗБАЛЛОВКИ к задачам муниципального этапа всероссийской олимпиады школьников по физике в 2020/2021 учебном году 11 класс 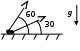 1. (10 баллов) Два тела бросили одновременно из одной точки на поверхности земли с одинаковой по величине начальной скоростью V0. Векторы начальных скоростей тел лежат в одной вертикальной плоскости и составляют с горизонтом углы 30 и 60 (см. рис.). Через какое время расстояние между телами достигнет максимального значения? Чему равно это максимальное значение? Ускорение свободного падения равно g. Ответ: Через время V0/g расстояние между телами достигнет максимального значения, равного 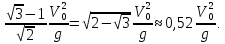 Решение: Наиболее короткое решение получается, если рассмотреть движение одного тела относительно другого. Поскольку ускорения тел одинаковы (равны ускорению свободного падения), то их относительная скорость не меняется со временем ни по направлению, ни по величине и остается равной ее начальному значению: 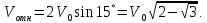 При этом расстояние R между телами растет со временем по закону 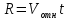 до тех пор, пока одно из тел не упадет на землю. Первым, через время до тех пор, пока одно из тел не упадет на землю. Первым, через время 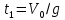 , упадет тело, брошенное под углом 30. В момент t1 тело, брошенное под углом 60, уже пройдет верхнюю точку своей траектории и заведомо будет приближаться к уже упавшему телу. Действительно, точки падения обоих тел совпадают из-за равенства дальностей полета ( , упадет тело, брошенное под углом 30. В момент t1 тело, брошенное под углом 60, уже пройдет верхнюю точку своей траектории и заведомо будет приближаться к уже упавшему телу. Действительно, точки падения обоих тел совпадают из-за равенства дальностей полета (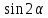 принимает одинаковые значения при принимает одинаковые значения при 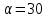 и и 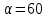 ). Таким образом, с момента t1 тела начнут сближаться, а максимальное расстояние между ними достигается в момент t1 и составляет ). Таким образом, с момента t1 тела начнут сближаться, а максимальное расстояние между ними достигается в момент t1 и составляет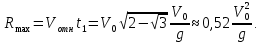 Другой способ решения состоит в записи зависимостей координат тел от времени 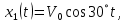 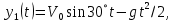 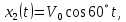 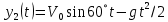 и вычислении расстояния между телами по формуле 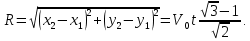 Повторяя приведенные выше рассуждения и подставляя в последнюю формулу время 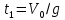 , приходим к тому же результату, но в несколько ином виде , приходим к тому же результату, но в несколько ином виде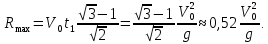 Разбалловка: Записаны зависимости координат тел от времени или найдена 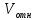 – 1 балл. – 1 балл. Записана зависимость расстояния между телами от времени – 3 балла. Понято, что тела упадут в одну точку – 2 балла. Доказано, что после падения одного из тел начнется их сближение – 1 балл. Найдено искомое время – 1 балл. Найдено максимальное расстояние – 2 балла. 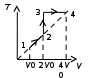 2. (10 баллов) Идеальный газ совершает процесс, состоящий из трех участков 1-2, 2-3 и 3-4 (см. риc.). На каком участке полученное газом тепло максимально? Ответ: Полученное газом тепло максимально на участке 23. 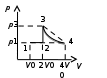 Решение: Изобразим процесс на плоскости p,V (см. рис.). Полученное газом тепло на участке 1-2 (изобара) равно Q12 = (5/2)p1V0. На участке 2-3 (изохора) полученное тепло равно Q23 = 3(p3 - p1)V0. Из уравнения Клапейрона-Менделеева для состояний 3 и 4 находим, что p3 = 2p1, поэтому Q23 = 3p1V0. Полученное тепло на изотермическом участке 3-4 равно совершенной газом работе, которую оценим сверху как площадь трапеции (площадь под отрезком жирной штриховой прямой): Q34 = A34 < (p1 + p3)V0 или Q34 < 3p1V0. Таким образом, полученное тепло максимально на участке 2-3. 3. (10 баллов) Два груза равной массы, подвешенные на одинаковых пружинах, совершают колебания в вертикальной плоскости. При прохождении грузами верхнего положения упругие энергии пружин равны, а при прохождении нижнего – отличаются в 4 раза. Найти отношение амплитуд колебаний грузов. Ответ: Отношение амплитуд равно 5. Решение: Нетрудно понять, что в верхнем положении одна пружина растянута на некоторую величину L, а другая сжата на такую же величину L. Обозначим через A1,2 соответствующие амплитуды колебаний грузов. Тогда в нижнем положении растяжение первой пружины можно записать как 2A1 + L, а второй – как 2A2 – L. Записывая соотношение между энергиями пружин в нижнем положении в виде 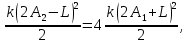 где k – коэффициент жесткости пружин, находим соотношение между амплитудами 2A2 – 4A1 = 3L. Еще одно соотношение между амплитудами можно получить из условия, что расстояния между положением недеформированной пружины и положением равновесия одинаковы у двух пружин, т.е. A1 + L = A2 – L. Из двух составленных выше уравнений получаем A1 = L/2, A2 = 5L/2, т.е. A2/A1 = 5. Разбалловка: Понято, что в верхнем положении одна пружина растянута, а другая сжата на ту же величину – 2 балла. Составлено одно уравнение для амплитуд – 3 балла. Составлено второе уравнение для амплитуд – 3 балла. Получен ответ – 2 балла. 10 класс 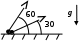 1. (10 баллов) Два тела бросили одновременно из одной точки на поверхности земли с одинаковой по величине начальной скоростью V0. Векторы начальных скоростей тел лежат в одной вертикальной плоскости и составляют с горизонтом углы 30 и 60 (см. рис.). Какого максимального значения достигнет расстояние между телами? Ускорение свободного падения равно g. 1. (10 баллов) Два тела бросили одновременно из одной точки на поверхности земли с одинаковой по величине начальной скоростью V0. Векторы начальных скоростей тел лежат в одной вертикальной плоскости и составляют с горизонтом углы 30 и 60 (см. рис.). Какого максимального значения достигнет расстояние между телами? Ускорение свободного падения равно g.Ответ: Через время V0/g расстояние между телами достигнет максимального значения, равного 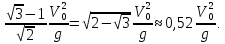 Решение: Наиболее короткое решение получается, если рассмотреть движение одного тела относительно другого. Поскольку ускорения тел одинаковы (равны ускорению свободного падения), то их относительная скорость не меняется со временем ни по направлению, ни по величине и остается равной ее начальному значению: 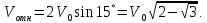 При этом расстояние R между телами растет со временем по закону 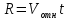 до тех пор, пока одно из тел не упадет на землю. Первым, через время до тех пор, пока одно из тел не упадет на землю. Первым, через время 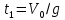 , упадет тело, брошенное под углом 30. В момент t1 тело, брошенное под углом 60, уже пройдет верхнюю точку своей траектории и заведомо будет приближаться к уже упавшему телу. Действительно, точки падения обоих тел совпадают из-за равенства дальностей полета ( , упадет тело, брошенное под углом 30. В момент t1 тело, брошенное под углом 60, уже пройдет верхнюю точку своей траектории и заведомо будет приближаться к уже упавшему телу. Действительно, точки падения обоих тел совпадают из-за равенства дальностей полета (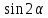 принимает одинаковые значения при принимает одинаковые значения при 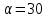 и и 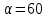 ). Таким образом, с момента t1 тела начнут сближаться, а максимальное расстояние между ними достигается в момент t1 и составляет ). Таким образом, с момента t1 тела начнут сближаться, а максимальное расстояние между ними достигается в момент t1 и составляет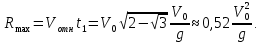 Другой способ решения состоит в записи зависимостей координат тел от времени 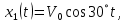 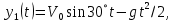 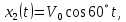 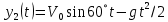 и вычислении расстояния между телами по формуле 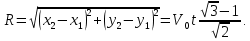 Повторяя приведенные выше рассуждения и подставляя в последнюю формулу время 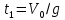 , приходим к тому же результату, но в несколько ином виде , приходим к тому же результату, но в несколько ином виде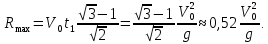 Разбалловка: Записаны зависимости координат тел от времени или найдена 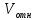 – 1 балл. – 1 балл. Записана зависимость расстояния между телами от времени – 3 балла. Понято, что тела упадут в одну точку – 2 балла. Доказано, что после падения одного из тел начнется их сближение – 1 балл. Найдено искомое время – 1 балл. Найдено максимальное расстояние – 2 балла.  2. (10 баллов) Жесткая невесомая проволочка с закрепленными на ней двумя равными точечными грузами удерживается в горизонтальном положении опорами на концах (см. рис.). Расстояние между грузами равно расстоянию от грузов до концов проволочки. Во сколько раз изменится сила, действующая со стороны одной из опор на проволочку, сразу после того, как другую опору убрать? 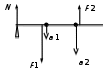 Ответ: Сила уменьшится в 5 раз. Решение: До того, как одну из опор убрали, каждая из них действовала на проволочку с силой mg, где m – масса одного груза, а g – ускорение свободного падения. После того, как одну из опор убрали, проволочка с грузами начинает вращение вокруг своего конца, находящегося на оставшейся опоре. В первый момент скорости грузов равны нулю и, следовательно, их ускорения чисто тангенциальные. Величины тангенциальных ускорений пропорциональны расстоянию до оси вращения, поэтому a2 = 2a1 (см. рис.). Сумма моментов сил, действующих на невесомую проволочку, должна быть равна нулю, иначе проволочка получит бесконечное угловое ускорение. Отсюда следует, что F1 = 2F2 и N = F2, где F1,2 – силы, действующие на проволочку со стороны грузов, а N – сила со стороны опоры (см. рис). Запишем второй закон Ньютона для каждого груза: ma1 = mg - F1, ma2 = mg + F2. Учитывая соотношения между ускорениями и силами, находим из этих уравнений, что F2 = mg/5. Следовательно, N = mg/5, что в 5 раз меньше начального значения. Разбалловка: Понято, что ускорения грузов чисто тангенциальные – 1 балл. Записано a2 = 2a1 – 2 балла. Понято, что F1 = 2F2 – 2 балла. Понято, что N = F2 – 2 балла. Записан второй закон Ньютона для каждого груза – по 1 баллу за груз. Получен ответ – 1 балл. 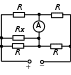 3. (10 баллов) В цепи, представленной на рисунке, сопротивления резисторов R равны 1 кОм, сопротивление амперметра пренебрежимо мало, напряжение на зажимах 120 В. Чему равно сопротивление Rx, если амперметр показывает 20 мА? Ответ: Сопротивление равно 1,25 кОм. Решение: Обозначив ток через верхний левый резистор через I, запишем для верхней ветви условие, что сумма напряжений на резисторах равна напряжению источника U = 120 В, т.е. IR + (I + 20)R = U. Отсюда находим, что I = 50 мА, а ток через верхний правый резистор равен 70 мА. В силу симметрии цепи в нижней ветви, составленной из резисторов R, текут такие же токи. Следовательно, через резистор Rx течет ток 40 мА. Сопоставляя токи через параллельно соединенные резисторы R и Rx, находим, что Rx = 1,25 кОм. 9 класс 1. (10 баллов) Частица движется прямолинейно с постоянным ускорением. Пройденный частицей путь и ее перемещение за промежуток времени 0 t t1 отличаются в три раза, скорость в момент t1 меньше по величине скорости при t = 0. Во сколько раз отличаются путь и перемещение за промежуток 0 t 2t1? Ответ: Путь больше перемещения в 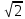 раз. раз.Решение: Ясно, что вектор ускорения частицы направлен против вектора начальной скорости и на интервале времени 0 t t1 частица движется сначала в одну сторону, затем, после остановки, в обратную. Меньшая величина скорости в момент t1 по сравнению с начальной (в момент t = 0) означает, что частица не успевает вернуться в начальную точку к моменту t1. Обозначим через L перемещение частицы к моменту t1, т.е. ее удаление от начальной точки в этот момент. Тогда, очевидно, пройденный путь 3L можно разделить следующим образом: 2L – это путь от начальной точки до точки остановки и L – путь в обратном направлении. Обозначив время движения от начальной точки до точки остановки через t0 и ускорение частицы через a, запишем соотношения 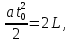 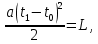 откуда находим, что 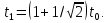 С момента t0 частица движется в одном направлении и за время 2t1 – t0 проходит путь С момента t0 частица движется в одном направлении и за время 2t1 – t0 проходит путь 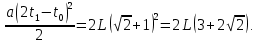 Тогда полный путь за время 0 t 2t1 равен 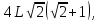 а перемещение за это время равно а перемещение за это время равно 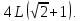 Таким образом, отношение этих двух величин равно Таким образом, отношение этих двух величин равно 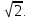 Разбалловка: Понято, что частица движется сначала в одном направлении, потом в другом – 1 балл. Понято, что частица не доходит до начальной точки к моменту t1 – 1 балл. Понято, что в момент t1 частица находится посередине между начальной точкой и точкой остановки – 1 балл. Получено соотношение между временем движения до остановки и t1 – 2 балла. Выражен путь за время 2t1 – 2 балла. Выражено перемещение за время 2t1 – 2 балла. Получен ответ – 1 балл. 2. (10 баллов) Ледяной шар радиуса R плавает в частично заполненном водой цилиндрическом сосуде с радиусом поперечного сечения 2R. Какой объем масла следует налить в сосуд для того, чтобы шар полностью оказался под поверхностью масла? Плотность воды 1000 кг/м3, плотность льда 900 кг/м3, плотность масла 800 кг/м3. Ответ: 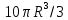 . .Решение: Запишем условие плавания полностью погруженного шара в виде  где через V1 и V2 обозначены части объема шара, находящиеся в воде и масле соответственно, через   и и  плотности воды, масла и льда, а через g ускорение свободного падения. Подставляя в это уравнение значения плотностей, находим, что V1 = V2, т.е. половина шара находится в воде, а половина в масле. Это означает, что толщина слоя масла равна радиусу шара. Учитывая, что шар занимает в масляном слое объем, равный половине объема шара, находим объем масла как плотности воды, масла и льда, а через g ускорение свободного падения. Подставляя в это уравнение значения плотностей, находим, что V1 = V2, т.е. половина шара находится в воде, а половина в масле. Это означает, что толщина слоя масла равна радиусу шара. Учитывая, что шар занимает в масляном слое объем, равный половине объема шара, находим объем масла как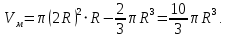 Разбалловка: Записано условие плавания полностью погруженного шара – 3 балла. Найдено, что шар погружен наполовину в воду, наполовину в масло – 2 балла. Понято, что толщина слоя масла равна радиусу шара – 2 балла. Найден объем слоя масла с половиной шара – 1 балл. Найден объем масла – 2 балла. 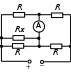 3. (10 баллов) В цепи, представленной на рисунке, сопротивления резисторов R одинаковы и равны 1 кОм, сопротивление амперметра пренебрежимо мало, напряжение на зажимах 120 В. Чему равно сопротивление Rx, если амперметр показывает 20 мА? Ответ: Сопротивление равно 1,25 кОм. Решение: Обозначив ток через верхний левый резистор через I, запишем для верхней ветви условие, что сумма напряжений на резисторах равна напряжению источника U = 120 В, т.е. IR + (I + 20)R = U. Отсюда находим, что I = 50 мА, а ток через верхний правый резистор равен 70 мА. В силу симметрии цепи в нижней ветви, составленной из резисторов R, текут такие же токи. Следовательно, через резистор Rx течет ток 40 мА. Сопоставляя токи через параллельно соединенные резисторы R и Rx, находим, что Rx = 1,25 кОм. 8 класс 1. (10 баллов) Два велосипедиста одновременно начинают движение по шоссе из одного пункта – один со скоростью 30 км/час, другой 25 км/час. Проехав 18 км, велосипедист, ехавший со скоростью 30 км/час, снизил ее до 20 км/час. Какое расстояние проедет каждый из велосипедистов к моменту, когда один догонит другого? Ответ: 30 км. Решение: Расстояние в 18 км велосипедист, ехавший со скоростью 30 км/час, преодолел за 18 : 30 = 3/5 часа. В течение этого времени велосипедисты удалялись друг от друга с относительной скоростью 30 – 25 = 5 км/час. После снижения скорости велосипедистом они стали сближаться с той же по величине относительной скоростью 25 – 20 = 5 км/час. При этом время сближения, очевидно, будет равно времени удаления, а полное время до встречи составит 6/5 часа. За это время велосипедист, ехавший с постоянной скоростью 25 км/час, преодолеет расстояние 30 км. Такое же расстояние проедет и другой велосипедист. 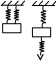 2. (10 баллов) При подвешивании тела на двух одинаковых легких пружинах (см. рис.) растяжение каждой из них составило 1 см. Затем одну из пружин прикрепили к телу снизу и, потянув за свободный конец (см. рис.), растянули ее опять на 1 см. Каким при этом стало растяжение верхней пружины? Ответ: 3 см. Решение: В первом случае сила упругости, действующая на груз со стороны каждой пружины, равна половине действующей на груз силы тяжести. По закону Гука сила упругости равна F = kx, где k – коэффициент жесткости пружины, а x – ее растяжение. Поскольку растяжение нижней пружины во втором случае такое же, как в первом, то эта пружина тянет груз вниз с силой, равной половине силе тяжести. Таким образом, полная направленная вниз сила на груз во втором случае равна 3/2 силы тяжести. Эту силу компенсирует упругая сила со стороны верхней пружины, следовательно, она в 3 раза больше, чем была в первом случае. А значит, ее удлинение также в 3 раза больше и составляет 3 см. Разбалловка: Записан закон Гука – 1 балл. Понято, что в первом случае сила каждой пружины равна половине силы тяжести– 2 балла. Понято, что во втором случае сила нижней пружины равна половине силы тяжести – 2 балла. Понято, что сила верхней пружины равна 3/2 силы тяжести – 3 балла. Найдено растяжение верхней пружины – 2 балла. 3. (10 баллов) Ледяной шар радиуса R плавает в частично заполненном водой цилиндрическом сосуде с радиусом поперечного сечения 2R. Какой объем масла следует налить в сосуд для того, чтобы шар полностью оказался под поверхностью масла? Плотность воды 1000 кг/м3, плотность льда 900 кг/м3, плотность масла 800 кг/м3. Ответ: 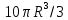 . .Решение: Запишем условие плавания полностью погруженного шара в виде 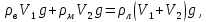 где через V1 и V2 обозначены части объема шара, находящиеся в воде и масле соответственно, через 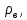 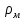 и и 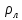 плотности воды, масла и льда, а через g ускорение свободного падения. Подставляя в это уравнение значения плотностей, находим, что V1 = V2, т.е. половина шара находится в воде, а половина в масле. Это означает, что толщина слоя масла равна радиусу шара. Учитывая, что шар занимает в масляном слое объем, равный половине объема шара, находим объем масла как плотности воды, масла и льда, а через g ускорение свободного падения. Подставляя в это уравнение значения плотностей, находим, что V1 = V2, т.е. половина шара находится в воде, а половина в масле. Это означает, что толщина слоя масла равна радиусу шара. Учитывая, что шар занимает в масляном слое объем, равный половине объема шара, находим объем масла как Разбалловка: Записано условие плавания полностью погруженного шара – 3 балла. Найдено, что шар погружен наполовину в воду, наполовину в масло – 2 балла. Понято, что толщина слоя масла равна радиусу шара – 2 балла. Найден объем слоя масла с половиной шара – 1 балл. Найден объем масла – 2 балла. 7 класс 1. (10 баллов) Два велосипедиста одновременно начинают движение по шоссе из одного пункта – один со скоростью 30 км/час, другой 25 км/час. Проехав 18 км, велосипедист, ехавший со скоростью 30 км/час, снизил ее до 20 км/час. Какое расстояние проедет каждый из велосипедистов к моменту, когда один догонит другого? Ответ: 30 км. Решение: Расстояние в 18 км велосипедист, ехавший со скоростью 30 км/час, преодолел за 18 : 30 = 3/5 часа. В течение этого времени велосипедисты удалялись друг от друга с относительной скоростью 30 – 25 = 5 км/час. После снижения скорости велосипедистом они стали сближаться с той же по величине относительной скоростью 25 – 20 = 5 км/час. При этом время сближения, очевидно, будет равно времени удаления, а полное время до встречи составит 6/5 часа. За это время велосипедист, ехавший с постоянной скоростью 25 км/час, преодолеет расстояние 30 км. Такое же расстояние проедет и другой велосипедист. 2. (10 баллов) Два куба, ребра которых отличаются в 2 раза, составлены из половин разной плотности. Плотности одних половин одинаковы у разных кубов, плотности других отличаются в 1,5 раза – большая у куба с большим ребром. Чему равно отношение плотностей половин меньшего куба, если отношение масс кубов равно 9? Ответ: Плотности относятся как 3 : 1. Решение: Обозначим плотности половин меньшего куба через 1 и 2, большего – через 1 и 1,52, ребро меньшего куба через a. Тогда массу большого куба можно записать как M = 2(21 + 32)a3, а малого как m = (1 + 2)a3/2. Накладывая условие M = 9m, приходим к соотношению 1 = 32. Разбалловка: Записана общая формула связи массы, плотности и объема – 1 балл. Записаны массы половин меньшего куба – по 1 баллу за половину. Записана масса всего меньшего куба – 1 балл. Записаны массы половин большего куба – по 1 баллу за половину. Записана масса большего куба – 1 балл. Составлено уравнение для нахождения отношения плотностей – 2 балла. Получен правильный ответ – 1 балл. 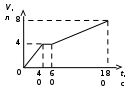 3. (10 баллов) Два цилиндрических сосуда одинаковой высоты и разного поперечного сечения стоят рядом на горизонтальном столе и соединены на середине высоты тонкой трубкой, образуя сообщающиеся сосуды. Один из сосудов частично заполнен водой, другой пуст. С момента t = 0 в пустой сосуд равномерно наливают воду до полного заполнения обоих сосудов. График зависимости объема воды в сосуде, в который наливают воду, от времени приведен на рисунке. Сколько литров воды наливают в секунду? Какой объем воды был в сосуде до наливания? Во сколько раз отличаются сечения сосудов? Объемом соединительной трубки пренебречь. Ответ: В секунду наливают 0,1 л. В сосуде было 6 л воды. Сечение частично заполненного водой сосуда в 2 раза большего сечения пустого сосуда. Решение: Участок графика на интервале 0-40 с соответствует заполнению половины пустого сосуда со скоростью 4 : 40 = 0,1 л/с. Объем всего пустого сосуда вдвое больше налитого за этот промежуток объема воды и равен 8 л. На интервале 40-60 с вода переливается в другой сосуд, который был частично заполнен вначале. За этот промежуток туда переливается 2 л воды. На интервале 60-180 с идет заполнение обоих сосудов до краев. При этом за 180 – 60 = 120 с в сосуды наливают 0,1 120 = 12 л воды. Таким образом, суммарный объем половин обоих сосудов равен 12 л, а суммарный полный объем обоих сосудов равен 24 л. Вычитая найденный выше объем пустого сосуда (8 л), находим объем сосуда, который был частично заполнен: 24 – 8 = 16 л. Поскольку высоты сосудов одинаковые, то сечение частично заполненного сосуда в 2 раза больше сечения пустого сосуда. Объем половины частично заполненного сосуда равен 8 л, и до заполнения этой половины в нее перелилось 2 л на интервале 40-60 с. Значит, в этом сосуде с самого начала было 8 – 2 = 6 л воды. Разбалловка: По участку 0-40 с найдена скорость наливания – 1 балл. Найден объем пустого сосуда – 1 балл. Понято, что на участке 40-60 с идет перелив в другой сосуд – 1 балл. По участку 60-180 с найден суммарный объем (половин) сосудов – 2 балла. Найден объем частично заполненного сосуда – 2 балла. Найдено отношение сечений сосудов – 1 балл. Найдено, какой объем воды был в сосуде до наливания – 2 балла. |
