Решение. Решение Запишем второй закон Ньютона для тела т1 в проекции на ось Оу (рис 1) и основное уравнение вращательного движения для маятника Обербека (моментом сил трения здесь пренебрегаем)
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
 где Iz - момент инерции маятника Обербека относительно оси Oz еz - угловое ускорение в проекции на ось Oz, ΣMizni=1 - алгебраическая сумма моментов сил, действующих на маятник в проекции на ось Oz. В дальнейших выкладках индекс z опускаем. Определение момента инерции грузов, находящихся на стержнях маятника Обербека
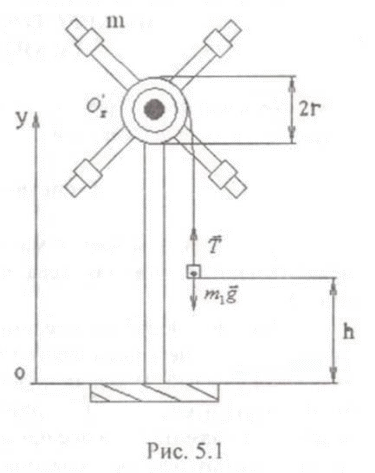 Указания к решению. Момент инерции маятника Обербека с закреплёнными на стержнях грузами т обозначим I = Iгр+I0, где Iгр — момент инерции грузов, I0 — момент инерции маятника Обербека без грузов. Решение: Запишем второй закон Ньютона для тела т1 в проекции на ось Оу (рис.5.1) и основное уравнение вращательного движения для маятника Обербека (моментом сил трения здесь пренебрегаем):  Соотношения (5.1) и (5.2) необходимо дополнить кинематическим уравнением движения груза  В случае, когда грузы сняты со стержней маятника Обербека, уравнения (5.1) , (5.2) и (5.3) примут вид  При решении систем уравнений (5.1) - (5.3) и (5.4) - (5.6) учитываем, что а| = и а2 = е2г (нить не проскальзывает). Отсюда получаем  Формула (5.7) используется в данной работе для экспериментального определения момента инерции четырёх грузов, закреплённых на стержнях маятника Обербека. Полученные в опыте значения Iгр необходимо сравнить с теоретическим значением момента инерции IТ, считая грузы точечными массами. где R - расстояние от оси вращения до центра масс каждого груза. При этом грузы на стержнях должны быть расположены на одном и том же расстоянии от оси вращения. Описание экспериментальной установки
 На вертикальной стойке закреплены четыре кронштейна, на которых закреплены блок 5, датчик 6 начала отсчёта времени вертикального движения груза (Рис. 5.2), датчик 9 окончания отсчёта времени движения этого груза. Сам маятник Обербека состоит из цилиндрической муфты с двумя шкивами 7 и 8 разного диаметра. В муфту ввинчены четыре жёстких стержня 4, на которых находятся грузы 3. Грузы на стержнях могут перемещаться. Один конец нити закрепляется на одном из шкивов и наматывается на него. Намотанная на шкив нить перекидывается через блок 5. К другому концу нити прикрепляется груз (показан на Рис. 5.3). На вертикальной стойке закреплена линейка для отсчёта положения этого груза. Маятник Обербека готов к опыту, когда груз перемещён вверх и находится на оптической оси датчика начала отсчёта времени 6. Оптическая ось датчика 6 должна находиться вблизи верхнего основания груза. При этом включённый секундомер должен показывать нулевое значение времени начала отсчёта. Датчики 6 и 9 выдают сигналы начала и окончания отсчёта времени движения груза на секундомер 2. Начальное положение груза 6 определяется координатой его нижнего торца по шкале линейки. Путь, пройденный грузом, определяется по разности начального положения нижнего торца груза и положения оптической оси датчика 9. Порядок выполнения работы 1. Заполнить табл. 5.1 спецификации измерительных приборов и записать данные установки (в том числе массу грузов на стержнях т = 200 г.; массу груза, скреплённого с нитью т1 = 60,7 г). 2. Снять четыре груза со стержней маятника. 3. Намотать нить с грузом на один из шкивов маятника и перекинуть её через блок так, чтобы середина груза т1, находилась на оптической оси датчика начала отсчёта времени 6. При этом необходимо придерживать маятник (за стержень) 4. Установить стойку 9 в вертикальное положение вращением ножек подставки 1. 5. Включить секундомер 2. Если груз на нити т1 перекрывает оптическую ось датчика начала отсчёта времени 6, то на дисплее секундомера должны быть мерцающие нули. Произвести отсчёт положения груза по координате его нижнего торца. Произвести отсчёт положения оптической оси датчика 9 по координате метки нанесённой на кронштейне датчика. Данные занести в табл. 5.2. 6. Отпустить стержень маятника. 7. После остановки движущегося на нити груза (попадания груза в ловушку) занести показания секундомера т2 в табл. 5.2. 8. Опыт повторить 5 раз. 9. Закрепить грузы массой m на середине стерней маятника так, чтобы их центры масс находились на одном и том же расстоянии от оси вращения. Это можно добиться проверкой устойчивого равновесия маятника при расположении каждой пары стержней с грузами в горизонтальном положении. Определить среднее расстояние R от центра масс грузов ш до оси вращения. Для этого измерить линейкой расстояния между наружным торцом одного груза и внутренним торцом противоположного груза для каждой пары грузов: для одной пары противоположных грузов, -для второй пары грузов. 10. Повторить пункты 3-7. Записать в таблицу показания секундомера 11. Опыт с грузами на стержнях повторить 5 раз. Исходные данные Приборы: Маятник Обербека (линейка на кронштейне маятника): 0 – 94 см (инстр. погрешность ± 0,5 мм); Линейка для измерения расстояний между грузами маятника: 0 – 30 см (инстр. погрешность ± 0,5 мм); Электронный секундомер (погрешность ± 0,001 сек); Масса грузов на стержнях m = 200 г.=0,2 кг; Масса груза, скреплённого с нитью m1 = 60,7 г=0,0607 кг.; Масса перегруза mп = 53,2 г=0,0532 кг.; r = 20 мм=0,002 м; g = 9,8 м/с 2 ; ∆g = 0,005 м/c2 ; y1 = 86 см=0,86 м; y2 = 9 см=0,09 м; l’ = 22,4 см=0,224 м; l’’ = 22,4 см=0,224 м; В лабораторной работе используем перегруз, т.е. m1 + mп. Значение времени, когда грузы m сняты с крестовины: t1 = 1,93 c; t2 = 1,87 c; t3 = 1,92 c; t4 = 1,94 c; t5 = 1,92 c; Значение времени, когда грузы m находятся на крестовине: t1 = 3,14 c; t2 = 3,16 c; t3 = 3,13 c; t4 = 3,13 c; t5 = 3,14 c; 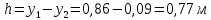  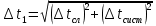     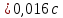   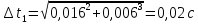   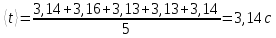   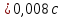   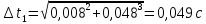 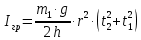  При t1ср = 1,92 c, t2ср = 3,14 c   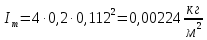       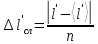 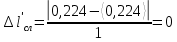   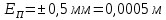  Δl′=Δl′′,т.к.l′=l′′= 0,0000015   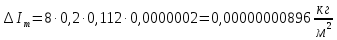 Ответы на контрольные вопросы 1. Как теоретически рассчитать момент инерции маятника Обербека? Какие параметры установки нужно для этого знать? Момент инерции – величина аддитивная, поэтому момент инерции маятника Обербека относительно его оси можно представить в виде суммы моментов инерции пяти тел: одной крестовины, состоящей из шкивов, подшипников и стержней и четырех тел (грузов), закрепленных на стержнях крестовины на одинаковом расстоянии R от оси вращения. Теоретическое значение момента инерции Iт, считая грузы точечными массами рассчитывают по формуле: Iт=4mR2 R - расстояние от оси вращения до центра масс каждого груза. При этом грузы на стержнях должны быть расположены на одном и том же расстоянии от оси вращения. m – масса каждого груза 2. Напишите основное уравнение динамики вращательного движения. Основное уравнение вращательного движения для маятника Обербека (моментом сил трения здесь пренебрегаем): T1r=Iε1 где: ε1- угловое ускорение, I - момент инерции, T1- натяжение нити, r- радиус шкива 3. Какая сила создает вращающий момент, действующий на маятник? Запишите выражение для момента этой силы. Укажите направление вектора момента силы. Уравнение поступательного движения груза на нити m𝑎⃗=m𝑔⃗−T Вектор 𝑚𝑎⃗ направлен вниз. 4. Напишите соотношение, связывающее ускорение маятника Обербека и линейное ускорение груза. Линейная скорость и линейное ускорение точек нити равны скорости и ускорению груза. С другой стороны, нить намотана на барабан маятника, поэтому линейная скорость и линейное ускорение точек нити (и груза) равны скорости и ускорению точек на барабане маятника, соприкасающихся с нитью. Но барабан вместе с крестовиной совершают вращательное движение, поэтому, для твердого тела. Ускорение маятника a=εR Ускорения груза a=mR2I+mR2g 5. В установке изменили положение грузов на стержнях. Как изменятся при этом параметры движения? Если сместить груза к центру увеличится скорость вращения маятника, а также увеличится скорость груза. Если сместить груза к краям стержней скорости маятника и груза уменьшатся. 6. Можно ли воспользоваться законом сохранения механической энергии для описания движения системы? Да, конечно, если система тел взаимодействует несколькими консервативными силами, и она замкнута, то закон сохранения полной механической энергии выполняется. |
