КОНТРОЛЬНАЯ РАБОТА № 2_математика. Контрольная работа № 2_1. Контрольная работа 2 по дисциплине Математика Вариант 1 Студент гр з 431П82 С. В. Михайлов Направления подготовки 09. 03. 01
 Скачать 156.23 Kb. Скачать 156.23 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) КОНТРОЛЬНАЯ РАБОТА № 2 по дисциплине «Математика» Вариант 1 Студент гр. з-431П8-2 С.В. Михайлов Направления подготовки 09.03.01. «11» марта 2022 г. Руководитель: канд. техн. наук, доцент кафедры АСУ А. И. Исакова «__ »________ 2022 г. 2022г. Найдите производные от данных функций: а) 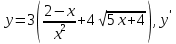 (1) (1)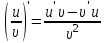 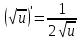 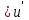 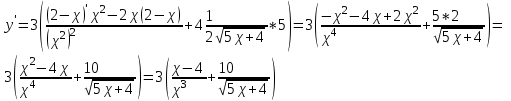 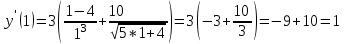 б) y= 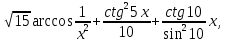 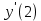 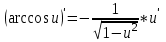 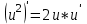 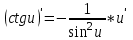 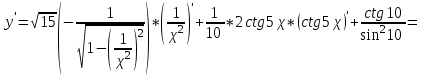 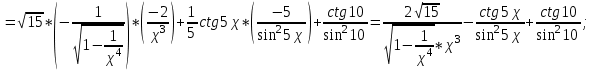  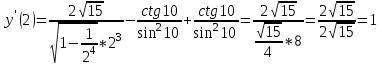 . .в) y=3 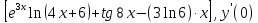 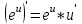 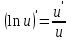 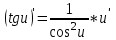 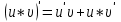 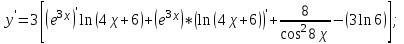 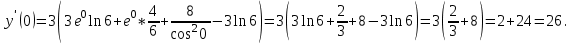 Дана функция: y= 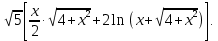 Найдите Найдите 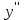 . Вычислите . Вычислите 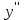 (1). (1).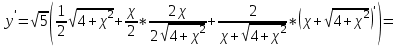 = 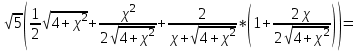 = 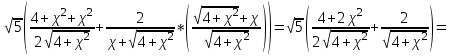 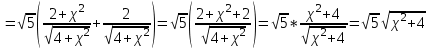 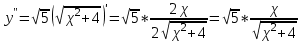 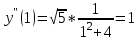 Дана функция 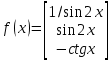 . Найдите . Найдите 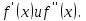 Вычислите Вычислите  . .Докажите, что функция z=sin(x+ay) удовлетворяет уравнению 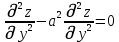 . .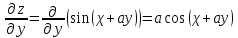 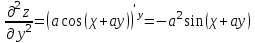 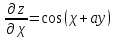 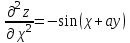 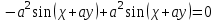 Дана функция Дана функция Найдите Функция z=z(x,y) задана неявно уравнением 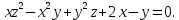 Вычислите: а) 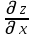 (0,1); (0,1);б) 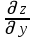 (0,1). (0,1).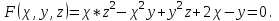 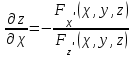 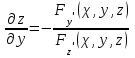 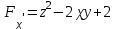 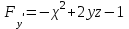 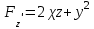 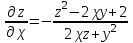 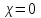 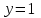 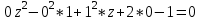 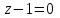 ; ; 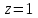 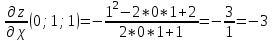 . .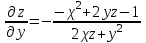 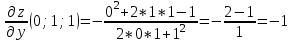 . .К графику функции Найдите Дана функция z= 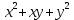 и точки и точки 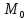 (1,2) и (1,2) и 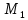 (1,02; 1,96). Вычислите ∆z и dz при переходе из точки (1,02; 1,96). Вычислите ∆z и dz при переходе из точки 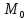 в точку в точку 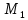 (ответы округлите до сотых). (ответы округлите до сотых).Дана функция y= 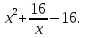 Найдите её наибольшее и наименьшее значение на отрезке [1,4]. Найдите её наибольшее и наименьшее значение на отрезке [1,4].Функция принимает наибольшее, наименьшее значения либо в критических точках, либо на концах отрезка. Найдем критические точки: 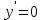 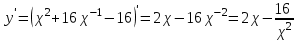 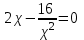 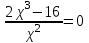 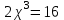 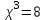 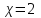 критическая точка критическая точкаНайдем значение функции в критической точке 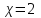 и на концах отрезка и на концах отрезка 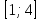 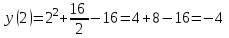 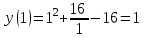 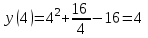  наибольшее=4, а наибольшее=4, а 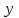 наименьшее=-4. наименьшее=-4.Дана функция z=(x- 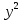 ) )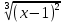 . Найдите её наибольшее и наименьшее . Найдите её наибольшее и наименьшеезначения на замкнутом множестве, ограниченном кривыми 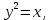 x=2. x=2.Проведите полное исследование функции y= 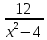 и начертите её график. и начертите её график.Область определения: 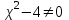 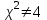 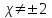 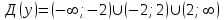 Решим вопрос о чётности 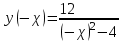 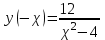 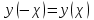 функция чётная, график симметричен относительно оси функция чётная, график симметричен относительно оси 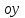 . .Исследуем на периодичность. Периодичности нет. Точки пересечения с осями координат: 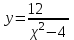 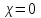 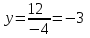 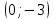 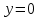 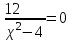 таких 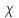 нет, с осью нет, с осью 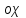 не пересекается не пересекаетсяТочки разрыва функции 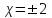 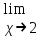 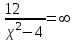 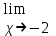 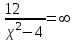 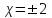 точка разрыва 2 рода. точка разрыва 2 рода.Проведем исследования на экстремум. 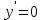 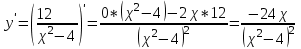 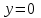 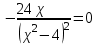 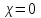 . .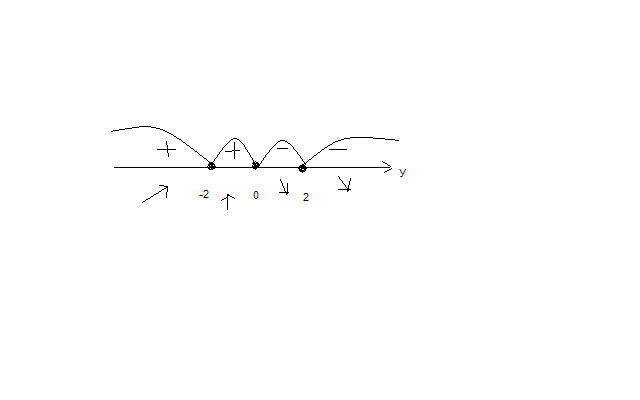 Определим знак производной в каждом интервале. Функция вырастает на 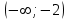 и и 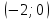 , ,Убывает на 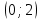 и и 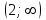 . .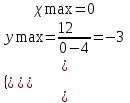 Найдем точки перегиба и интервалы выпуклости и вогнутости. 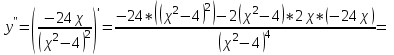 = 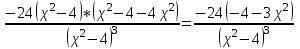 ; ;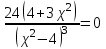 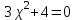 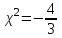 корней нет. корней нет.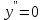 критических точек нет. критических точек нет.Исследуем область определения. 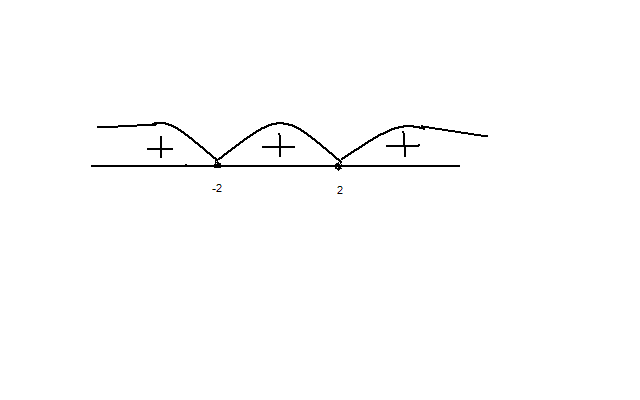 Выпуклый на 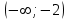 и и 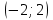 и и 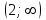 , точек перегиба нет. , точек перегиба нет.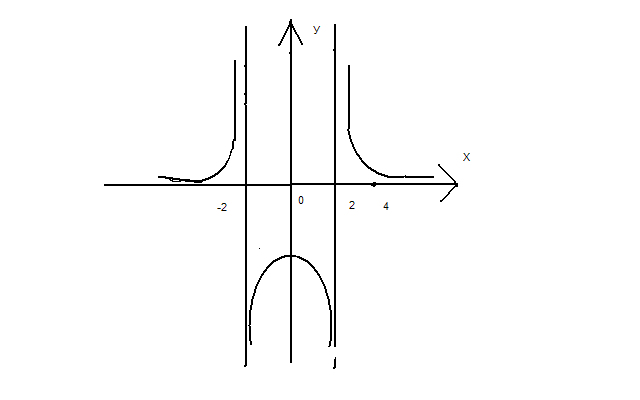 |
