радиоавтоматика (вариант 1)3. Контрольная работа 2 по дисциплине Радиоавтоматика
 Скачать 46.42 Kb. Скачать 46.42 Kb.
|
|
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Р.Е. Алексеева ИРИТ Контрольная работа 2 по дисциплине «Радиоавтоматика» Вариант 1 Выполнил: студент гр. 18-РТз Маницын Александр ст. билет № 1103011899 Проверила: Хлыбова С.С. 2022 г. Содержание Задание 1 3 Задание 2 4 Список литературы 7 Задание 1Передаточная функция разомкнутой системы имеет вид: 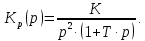 Определить порядок астатизма и значения 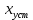 и и 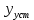 при воздействии на вход системы сигнала вида при воздействии на вход системы сигнала вида 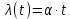 . .Решение Передаточная функция ошибки определяется по формуле: 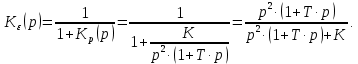 Передаточная функция ошибки имеет нуль второго порядка в точке 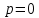 . Следовательно, порядок астатизма линейной непрерывной разомкнутой системы равен двум, т.е. . Следовательно, порядок астатизма линейной непрерывной разомкнутой системы равен двум, т.е. 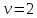 . .Переведём в пространство Лапласа временное выражение входного сигнала: 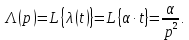 Получаем выражение для выходного сигнала в пространстве Лапласа: 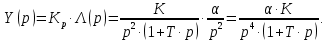 Определяем выражение для сигнала: 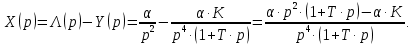 Далее определяем установившиеся значения сигналов: 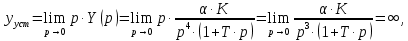 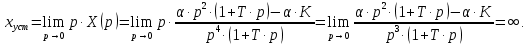 Задание 2Для линейной импульсной системы известен коэффициент передачи в разомкнутом виде 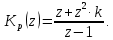 Определить: 1) необходимые и достаточные условия устойчивости; 2) условия устойчивости с помощью критерия Гурвица; 3) порядок астатизма и значения 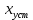 и и 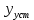 в тактовых точках при воздействии на вход системы сигнала вида в тактовых точках при воздействии на вход системы сигнала вида 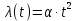 . .Решение Для устойчивости САУ необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения имели отрицательные знаки, то есть корни характеристического уравнения устойчивой системы на плоскости комплексного переменного были расположены слева от мнимой оси. Для передаточной функции в z-пространстве необходимо и достаточно, чтобы все корни лежали в пределах единичной окружности. В нашем случае, для заданной передаточной функции: 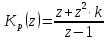 система будет неустойчивой, так как корень равен: 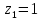 . .Переведём в z-пространство входной сигнал: 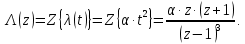 Получаем выражения для сигналов в пространстве z: 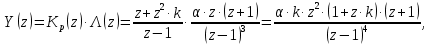 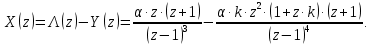 Определим условия устойчивости по критерию Гурвица. 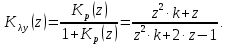 Запишем характеристическое уравнение: 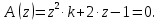 Делаем замену в характеристическом уравнении: 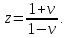 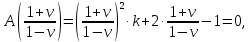 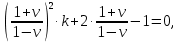 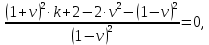 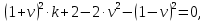 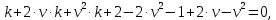 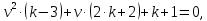 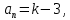 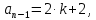 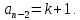 Составляем матрицу Гурвица: 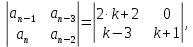 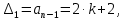 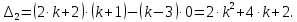 Решаем уравнения: 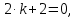 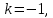 т.е. 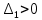 при при 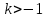 . .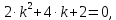 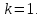 Т.е. 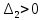 при при 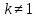 . .Таким образом, система будет устойчивой при 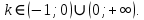 Определим порядок астатизма: 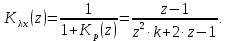 Порядок астатизма равен 0 (по степени 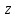 в числителе). в числителе).Определим установившиеся значения сигналов. 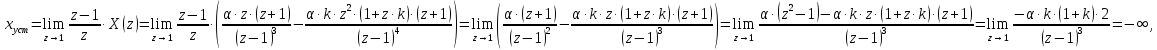 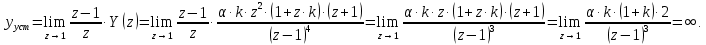 Определим необходимые и достаточные условия устойчивости. 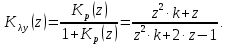 Запишем характеристическое уравнение: 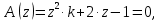 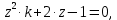 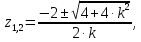 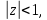 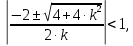 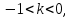 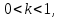  Таким образом, система будет устойчивой при 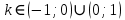 . .Список литературыБесекерский В.А. Теория систем автоматического управления. – М., 2003. Воронов А.А. Теория автоматического управления. Теория линейных систем автоматического управления ч.1, 1986. Гайдук А.Р. Системы автоматического управления. Примеры, анализ и синтез. – М., 2006. |
