Контрольная работа 2 высшая математика ТУСУР. Контрольная работа № 2. Контрольная работа 2 Вариант 2. 5 1(Д01. Рп). Составить общее уравнение прямой, проходящей через точку М(14)
 Скачать 101.19 Kb. Скачать 101.19 Kb.
|
|
Томский Государственный Университет Систем Управления и Радиоэлектроники Контрольная работа № 2 Вариант №2.5 1(Д01.РП). Составить общее уравнение прямой, проходящей через точку М(1;4) параллельно прямой 2х+3у+5=0. Решение. В качестве вектора нормали можно принять вектор N =(2;3) и записать искомое уравнение, используя формулу Ах + Ву – (Ах0+Ву0) =0, 2х+3у – (2+12)=0, 2х+3у – 14 =0. Ответ: 2х+3у – 14 =0. 2(3А2.РП) Найти координаты проекции точки М(3;6) на прямую L, заданную уравнением х+2у – 10 = 0. Решение. Точку Q, являющуюся проекцией точки М на данную прямую, можно найти как точку пересечения прямой L и отрезка MQ, перпендикулярной данной и проходящей через точку М. Прямая MQ параллельна вектору N1(1,2) – нормали прямой L. В качестве вектора нормали прямой MQ можно принять вектор N2 (-2,1), следовательно, уравнение прямой имеет вид -2х+у-(-6+6) или –2х+у=0. Получаем систему уравнений:      у=2х y=2x y=2x y=2x у=4 Ответ: Q(2;4). 3(103.БЛ) Записать общее уравнение плоскости, проходящей через три заданные точки М1 (-6;1;-5), М2 (7;-2;-1), М3 (10;-7;1). Решение. Данная плоскость параллельна векторам L1= М1М2= (13;-3;4) и L2=М1М3 = (16;-8;6). Поэтому в качестве вектора нормали можно взять вектор  i j k N = [L1L2] = 13 -3 4 16 -8 6 Разложим этот определитель по первой строке:    N= -3 4 *i - 13 4 *j + 13 –3 *k = 14i – 14j – 56k, -8 6 16 6 16 –8 следовательно N = (14;-14;-56) Записываем уравнение плоскости 14х – 14у –56z +С =0. Для определения С используем условие, что плоскость проходит через точку М1 (-6;1;-5): -84-14+280+С+0. Отсюда, С= -182. Для остальных двух точек С будет так же равным -182. Следовательно, общее уравнение плоскости будет: 14х - 14у - 56 – 182=0, х-у-4z-13=0. Ответ: х-у-4z-13=0. 4(203) Известно, что прямая L параллельна вектору l = (0;9;12). Найти длину отрезка этой прямой между плоскостями х+у+z – 3=0 и х+у+z – 24=0. Решение. Рассмотрим расположение плоскостей х+у+z–3=0 и х+у+z–24=0 в пространстве. Нормали плоскостей N1 и N2 равны, следовательно, плоскости параллельны, а т.к. A1/A2 = B1/B2=C1/C2≠D1/D2, то плоскости не совпадают. Т.к. прямая L параллельна вектору l=(0;9;12), то уравнение прямой примет вид: 9у+12z + D=0. Пусть D=0, тогда уравнение прямой примет вид:  9у+12z=0. Найдём точки пересечения прямой с плоскостями. Запишем уравнение прямой L в параметрическом виде: 9у= -12z. Примем z за свободный член, тогда у = -12t / 9 z = t Находим то значение параметра t1, при котором происходит пересечение прямой и плоскости х + у + z – 3 =0. Так как точка М (0;-12t/9;t) лежит в данной плоскости, то её координаты удовлетворяют уравнению плоскости, следовательно, -12t1/9+t1-3=0, -12t1+9t1-27=0, -3t1=27, t1 = -9. Для плоскости х + у + z – 24=0 t2 находим –12t2/9+t2-24=0, -12t2+9t2 -216=0, -3t2=216, t2=-72. Полагая в параметрическом уравнении прямой t1= -9 и t2= -72 находим точки пересечения М1 (0; 12;-9) и М2 (0;96;-72). Имея формулу расстояния между двумя точками в пространстве, находим отрезок М1М2 между двумя данными плоскостями:  D= √(x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2 ,   M1M2=√ (96-12)2 + (-72+9)2 = √7056+3969 = 105. Ответ: 105. 5(3С2) Некоторая прямая проходит через точку Р (2;2;1), пересекает ось ординат  в точке Q (0;у0;0) и пересекает прямую х-3z+2=0 Найти y0. y-2z+1=0. Решение.  Приняв z за свободный член, преобразуем данное уравнение прямой при z=t, х=3t-2, y=2t-1 z=t Условием пересечения двух прямых является равенство (r2-r1;l1;l2)=0. В нашем случае r2=(2;2;1), r1=(-2;-1;0), l1=(3;2;1), l2=PQ=(-2;y0-2;-1).  4 3 1    Находим (r2-r1,l1,l2) = 3 2 1 = -2* 3 1 - (у0-2)* 4 1 -1* 4 3 = -2 у0-2 –1 2 1 3 1 3 2 = -2 - (у0-2)-2=0, -4-у0+2=0, -2-у0=0, у0=2. Ответ: 2. 6(7АД) Плоскость содержит прямую x/3 = у/0 = (z-6)/-2 и параллельна прямой х-3 = у-3 = -2(z-6). Найти квадрат расстояния от второй прямой до плоскости. Решение. Преобразуем данные канонические уравнения прямых. 2х+3z-18=0 – прямая в плоскости, х+у-4z-18=0 – прямая, параллельная плоскости. Т.к. A1/A2≠B1/B2≠C1/C2 , то прямые не параллельны, и т.к. одна из прямых содержится в плоскости параллельной второй прямой, то прямые являются скрещивающимися. Нахождение отрезка между плоскостью и второй прямой сводится к нахождению отрезка между двумя скрещивающимися прямыми. Переведём уравнения прямых от канонического к параметрическому виду. 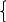 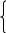 x/3 = у/0 = (z-6)/-2, отсюда х=3t и х-3=у-3=-2(z-6), отсюда x=t+3 z=-2t+6 y=t+3 z=Ѕt+6 Зная формулу |(r2-r1,l1,l2)/|[l1,l2]|, где r1=(0;0;6), r2=(3;3;6), l1=(3;0;-2), l2=(1;1;Ѕ)     находим 3 3 0 0 –2 3 –2 3 0 r2 - r1,l1,l2 = 3 0 –2 = i* 1 Ѕ - j* 1 Ѕ + k* 1 1 = -2i+Ѕj+3k. 1 1 Ѕ   D2= (4,5/√4+0,25+9)2 = (4,5/√13,25)2 = 4,52/13,25 = 20,25/13,25=81/53 Ответ: 81/53. 7(C04.РП) Доказать, что уравнение х2 + у2 + 6х - 10у - 15= 0 определяет на плоскости XOY окружность. Найти её центр и радиус R. Решение. Уравнение вида a11x2+a22y2+2a12xy+a01x+a02y+a00=0 определяет на плоскости окружность, если а11=а22≠0, а12=0. В нашем случае данное уравнение удовлетворяет условию, поэтому, х2+у2+6х-10у-15=0 определяет на плоскости XOY окружность. Найдём радиус и центр данной окружности. Преобразуем данное уравнение, выделив полные квадраты: (х+3)2+ (у-5)2=49. Отсюда, центр окружности – (3;-5), и R= 49 Ответ: (3;-5), R=49. 8. Дана кривая 4х2-у2- 24х+4у+28=0. 8.1 Доказать, что это кривая - гипербола. Решение. Выделяя полные квадраты, данное уравнение можно записать в виде 4(х-3)2-(у-2)2=4 или (х-3)2/1- (у-2)2/4=1. Следовательно, данное уравнение описывает гиперболу. 8.2(325.Б7). Найти координаты её центра симметрии. Решение. Положим х1=х-3, у1=у-2. Тогда х12 / 1 – у12 /4 =1. Данная кривая – гипербола с центром в точке х1 = х-3=0, у1 = у-2 = 0, т.е. в точке (3,2). 8.3(Д06.РП). Найти действительную и мнимую полуоси. Решение. Т.к. гипербола задана уравнением x2 / а2 - у2 /b2 = 1, то мнимой полуосью является число b, в нашем случае b=4, а действительная полуось а=1. 8.4 (267.БЛ). Записать уравнение фокальной оси. Решение. Т.к. в нашем случае фокусы расположены на прямой параллельной оси ОХ, то уравнение фокальной оси примет вид у=2. 8.5 Построить данную гиперболу. Решение. Строим прямоугольник со сторонами 2а и 2b. Проводим его диагонали. На оси ОX2 откладываем фокусы F1 и F2, равные половине диагонали. Затем, берём любые точки на оси ОХ2 и подставляем их в формулы радиусов фокусов: 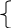 r1 = -a+εx, для точек правой ветви гиперболы; r2 = a+εx 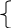 r1 = a-εx, для точек левой ветви гиперболы. r2 = -a-εx Точки пересечения соответственных дуг будут являться точками гиперболы. Выбирая точки на оси ОX2 левее фокуса F2, строим аналогично точки левой ветви параболы. 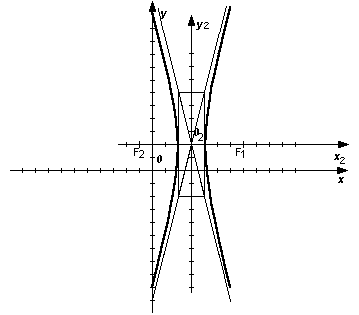 9. Дана кривая у2+6х+6у+15=0. 9.1 Доказать, что данная кривая – парабола. Решение. Выделяя полный квадрат, получаем (у+3)2+6х+6=0. Если положить у1=у+3, х1= -6х-6, то уравнение приводится к виду у12= х1. Данное уравнение соответствует каноническому уравнению параболы. 9.2(058.РП). Найти координаты её вершины. Решение.  -6х-6=0 Отсюда y = -3; x = -1. Следовательно, вершина параболы находится в точке (-1,-3). 9.3(2П9). Найти значения её параметра p. Решение. Сравнивая приводимое уравнение с каноническим уравнением параболы, находим, что 2р=1; p = Ѕ. 9.4(289.РП). Записать уравнение её оси симметрии. Решение. Т.к. вершина параболы находится в точке (-1;-3), то уравнение оси симметрии является у = -3. 9.5. Построить данную параболу. Решение. Для построения данного графика необходимо выбрать любые точки на оси ОХ меньшие нуля, и подставить их в уравнение параболы у2+6х+6у+15=0. Полученные значения и будут являться точками параболы. 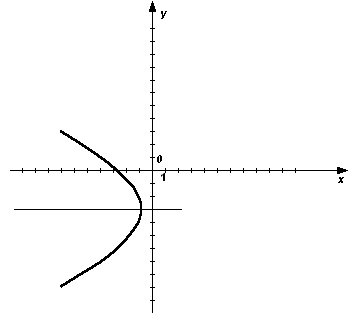 10. Дана кривая 5х2 + 5у2+ 6ху – 16x - 16у = 16. 10.1. Доказать, что эта кривая – эллипс. Решение.   3 5 3 5-λ (5-λ)(5-λ)-9=25-10λ+λ2-9 = λ2-10λ+16 =0. λ1=8, λ2=2. Т.к. λ1*λ2>0, то данная кривая является эллипсом. 10.2(822.РП). Найти координаты центра ее симметрии. Решение. 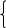 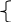 (5-8)ε1+3ε2=0, -3ε1+3ε2=0, 3ε1+(5-8)ε2=0; 3ε1- 3ε2=0; 3ε1=3ε2, ε1=ε2. Если положить ε1=1,ε2=1, то единичный собственный вектор i1 имеет координаты i1= (1/√2; 1/√2). Другой вектор j1=(1/√2;-1/√2). Записываем матрицу Q перехода от базиса О,i, j к O1,i1,j1.   Q = 1/√2 1/√2 , Q-1 = QT = -1/√2 -1/√2 1/√2 -1/√2 -1/√2 1/√2 Новые координаты(х1,у1) связаны со старыми (х ,у) соотношением: 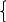 х1=-х-у/√2, у1=-х+у/√2; В новой системе координат уравнение 5х2 + 5у2+ 6ху - 16x - 16у = 16 примет вид 8х12 + 2у12 + -16(-1-1)х1/√2 + -16(-1+1)у1/√2 = 16, 8х12+2у12+16х1√2=16. После выделения полных квадратов получаем 8(х1+√2)2+2у12=32. Перейдём к новой системе координат O1,i1,j1 по формулам х2=х1+√2 и у2=у1. Теперь уравнение примет вид 8х22 + 2у22 =32, х22/4 + у22/16=1. Отсюда, х2=-х-у-2/√2, у2=-х+у/√2. Решая систему х2=0, у2=0, найдём центр симметрии и координаты нового начала O1 в старой системе координат:     -х - у-2=0, у=х, -2х=2, х=-1, -х+ у =0; -х-х-2=0; у =х; у=-1; О1(-1;-1). 10.3(470.Б7). Найти ее большую и малую полуоси. Решение. Зная уравнение х22/4+ у22/16=1 можно дать полную геометрическую характеристику данного эллипса. Так, большая полуось эллипса равна 4, а малая 2. 10.4(941.РП). Записать уравнение фокальной оси. Решение. Т.к. фокусы расположены на новой оси О1Х2, то уравнение фокальной оси примет вид –х+у = 0. 10.5. Построить данную кривую. Решение. 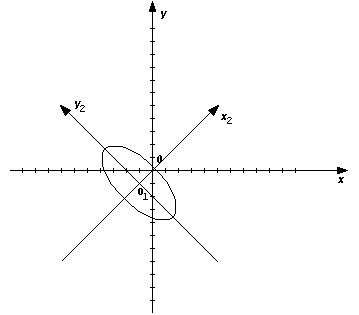 Список литературы: Учебно-методическое пособие Л. И. Магазинников, А. Л. Магазинникова |
