Контрольная работа 3 Аналитическая геометрия тема аналитическая геометрия Уравнения линии в декартовой системе координат. Параметрические уравнения линии
 Скачать 1.55 Mb. Скачать 1.55 Mb.
|
|
Задача №2. Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание. 1) Составить уравнение плоскости, проходящей через точки Решение. Уравнение плоскости, проходящей через точки 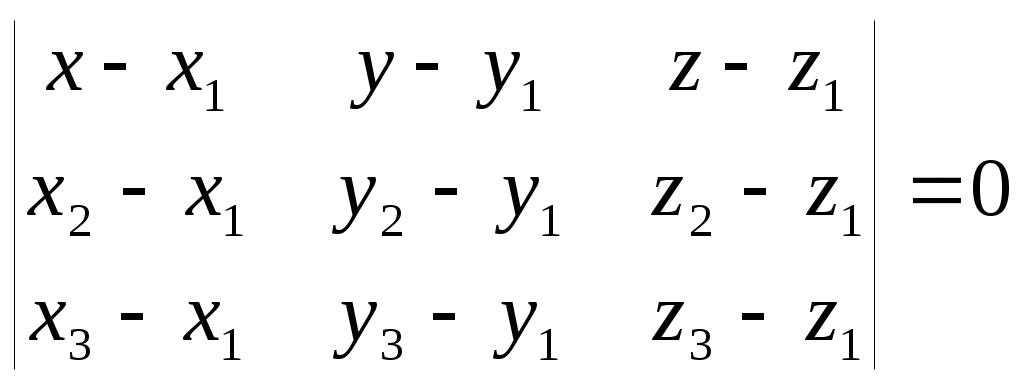 (3.7) (3.7)Тогда уравнение плоскости 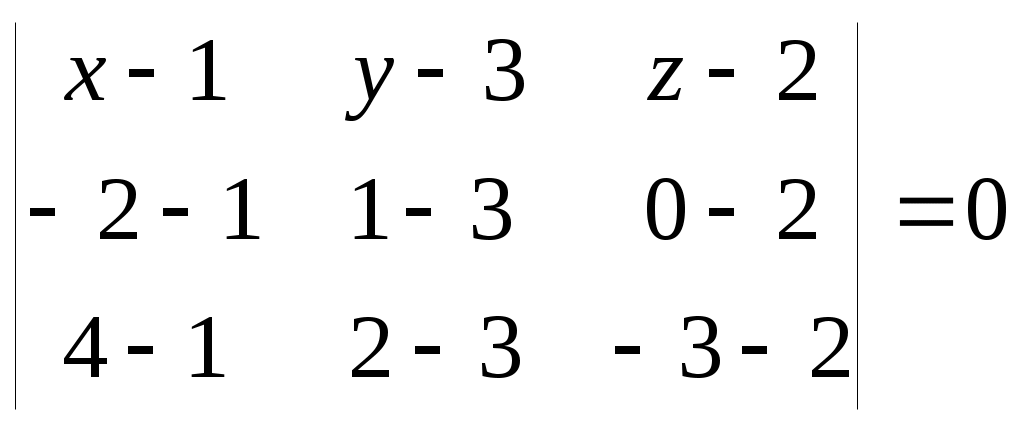 или или 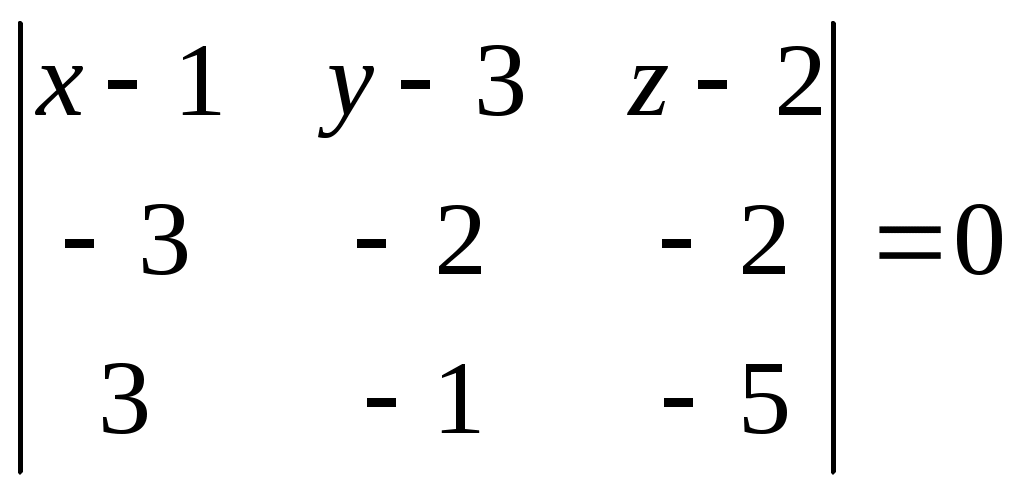 . . Запишем полученное уравнение в общем виде, т.е. в виде 2) Найти нормальный вектор плоскости Решение. Нормальный вектор  Рис. 3 Для плоскости Отметим, что любой вектор, коллинеарный вектору 3) Найти косинус угла между плоскостями Решение. Угол Для плоскости 4) Составить уравнение плоскости Решение. Уравнение плоскости, проходящей через точку Подставим в уравнение (3.8) координаты точки Условие параллельности плоскостей Так как плоскости 5) Найти расстояние от точки Решение. Расстояние Для плоскости 6) Составить канонические уравнения прямой, проходящей через точки Решение. Уравнения прямой, проходящей через точки Так как 7) Найти направляющий вектор прямой Решение. Направляющий вектор Если прямая задана каноническими уравнениями  Рис. 4 Для рассматриваемой прямой Отметим, что любой вектор, коллинеарный вектору 8) Найти косинус угла между прямыми Решение. Угол Для прямой 9) Составить канонические уравнения прямой Решение. Канонические уравнения прямой имеют вид В канонические уравнения прямой Условие параллельности прямых Так как прямые 10) Найти угол между прямой Решение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол 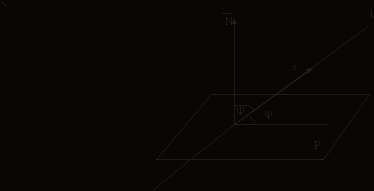 Рис. 5 Угол Для плоскости 11) Составить уравнение плоскости Решение. Уравнение плоскости, проходящей через данную точку, имеет вид Подставим в указанное уравнение координаты точки Условие перпендикулярности плоскости Так как искомая плоскость 12) Составить канонические уравнения прямой Решение. Канонические уравнения прямой, проходящей через данную точку, имеют вид Подставим в эти уравнения координаты точки Условие перпендикулярности прямой Так как прямая 13) Найти координаты точки пересечения прямой Решение. Координаты точки 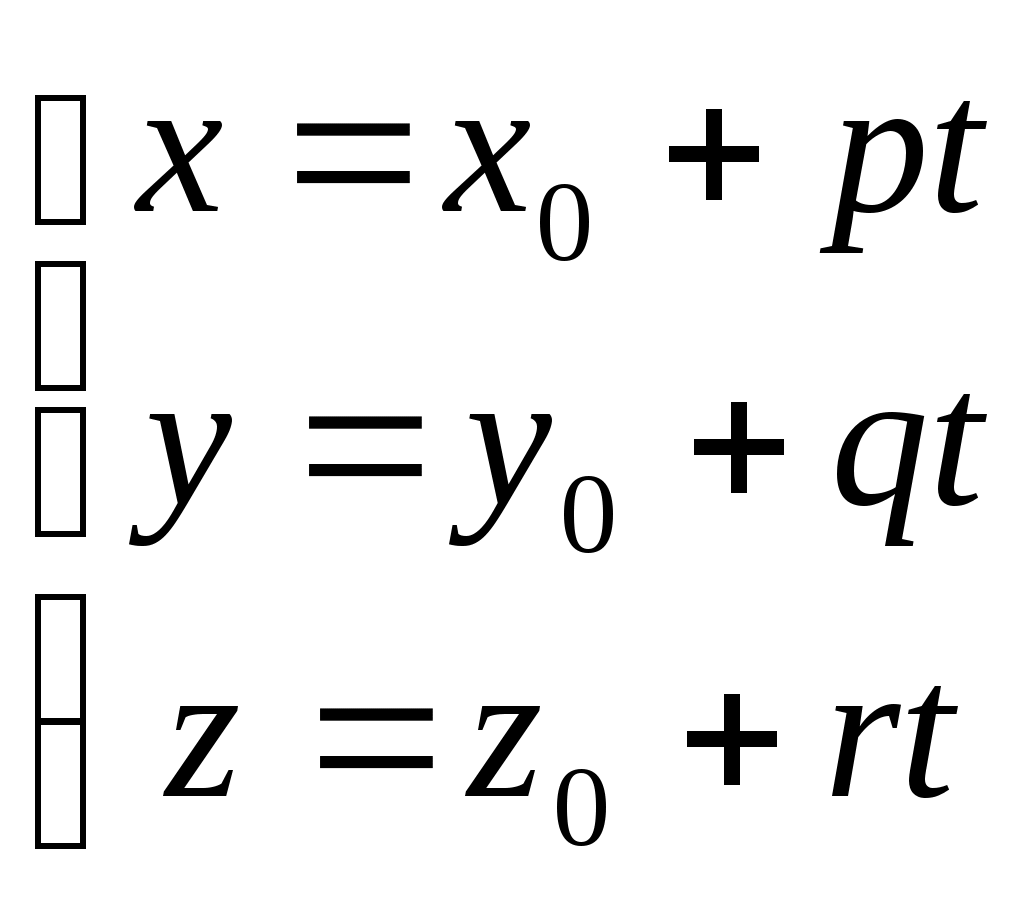 и плоскости и плоскости 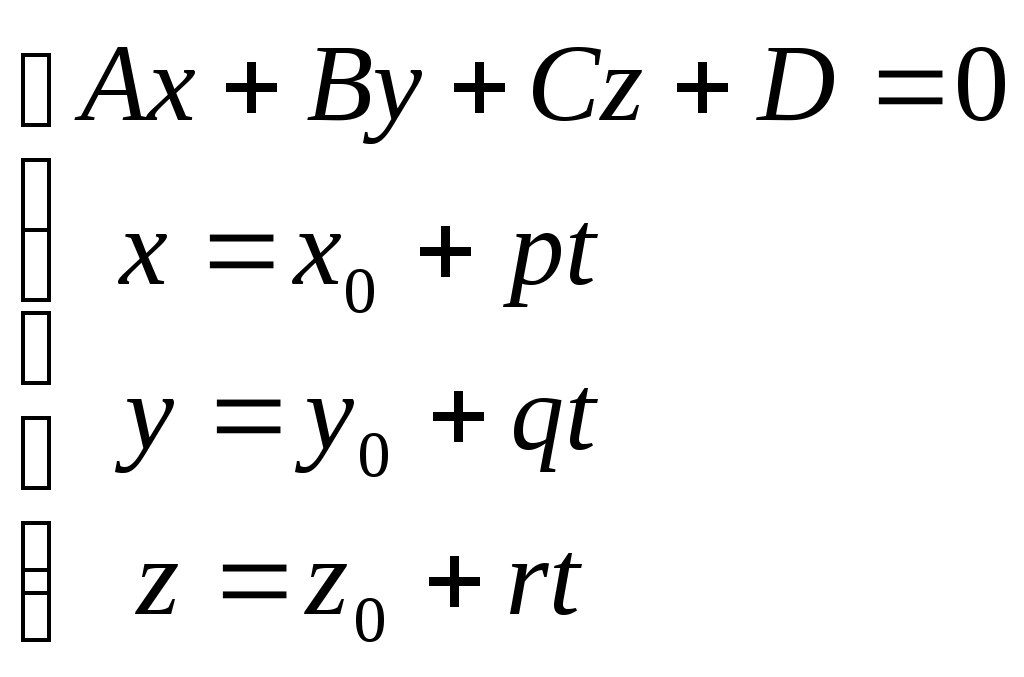 (3.14) (3.14)Запишем параметрические уравнения прямой 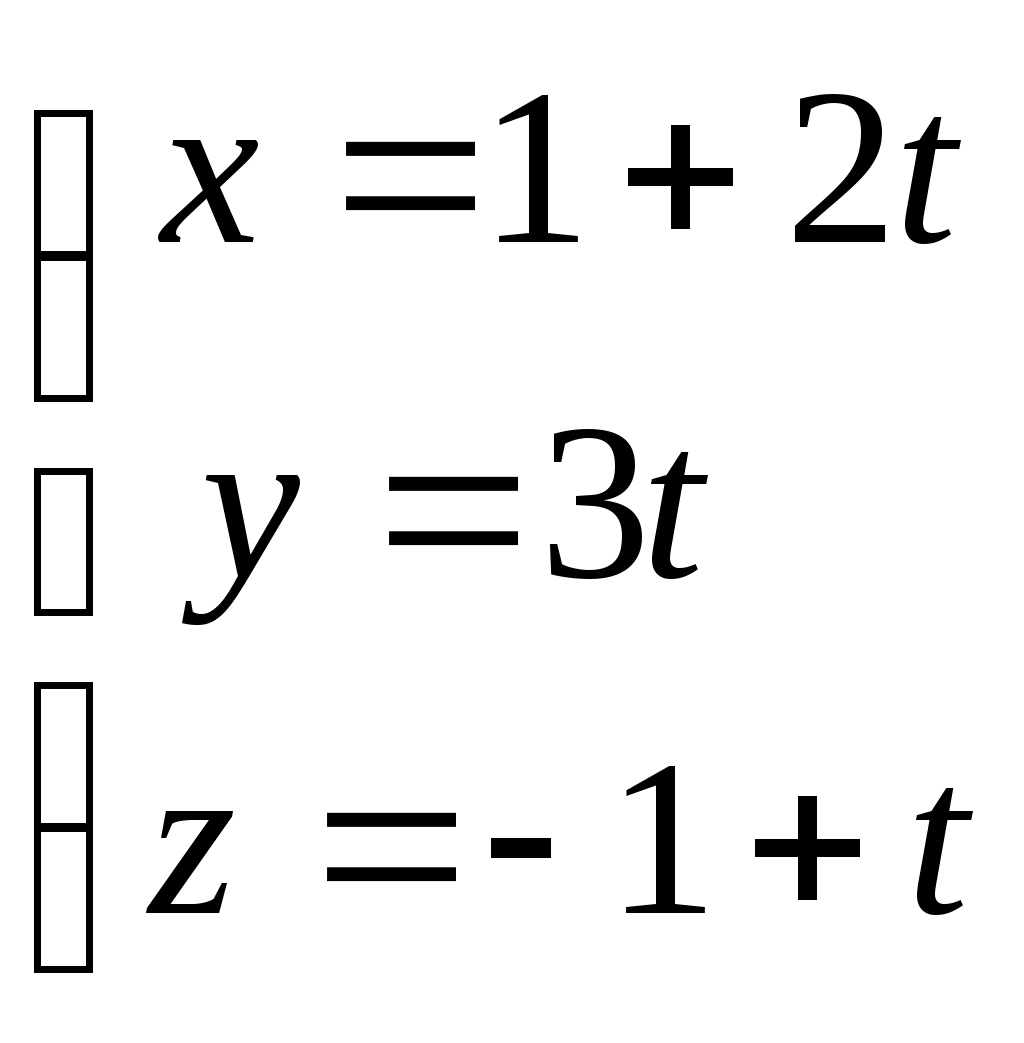 и подставим выражения для и подставим выражения для 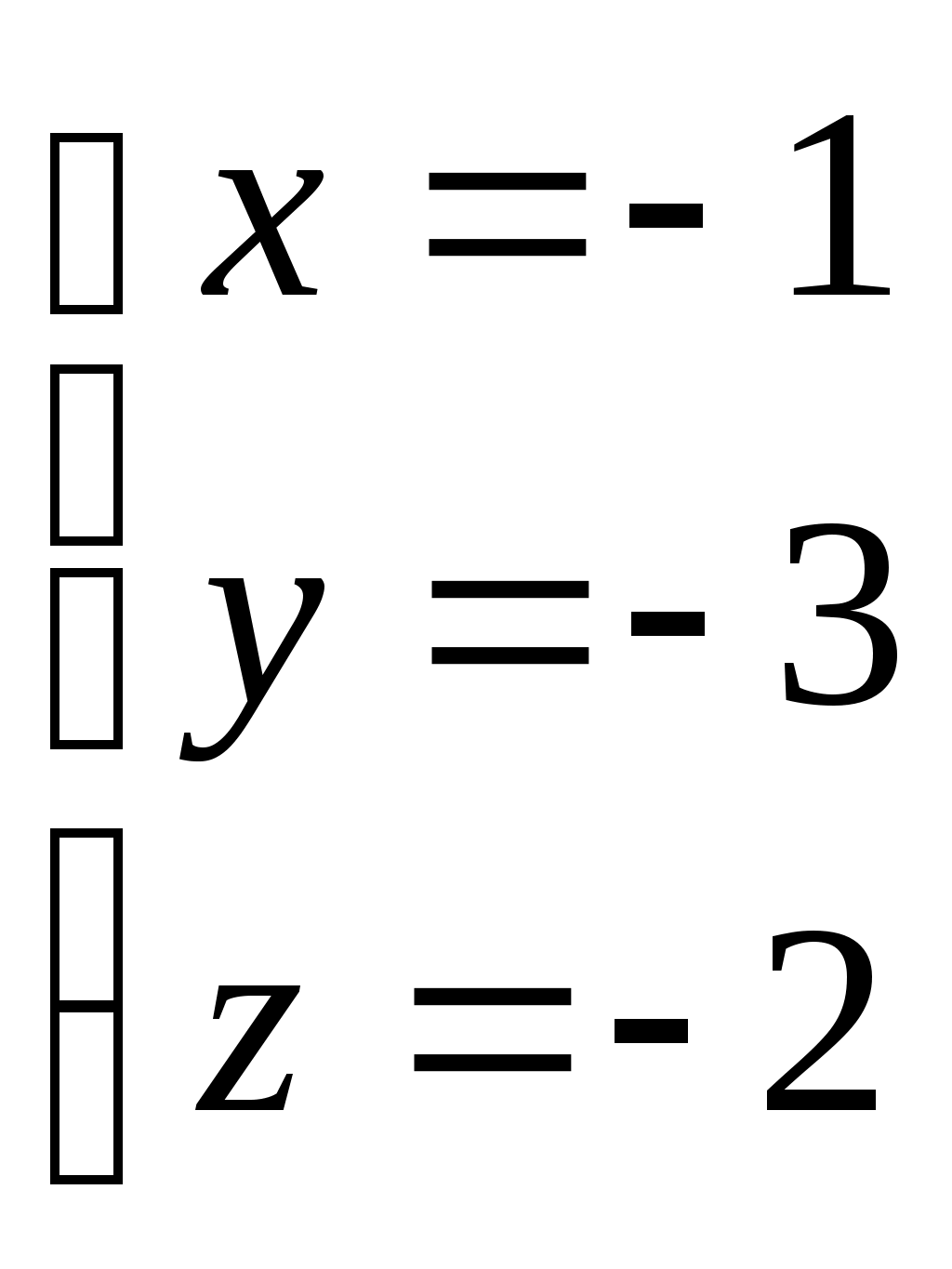 . Следовательно, . Следовательно, Задача №3. К кривым второго порядка относятся эллипс (рис.6), гипербола (рис. 7 и 8), парабола (рис. 9-12). Приведем рисунки и канонические уравнения этих кривых. Эллипс 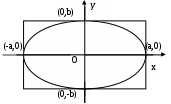 Рис. 6 Гипербола 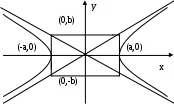 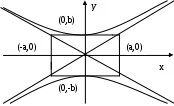 Рис. 7 Рис. 8 Парабола 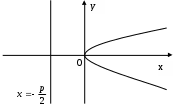 Рис. 9 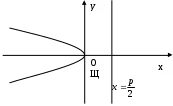 Рис. 10 Парабола 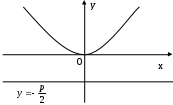 Рис. 11 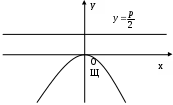 Рис. 12 Приведем примеры решения задачи №3. Пример 1. Привести уравнение кривой второго порядка Решение. Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата. Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при Выделим полный квадрат: 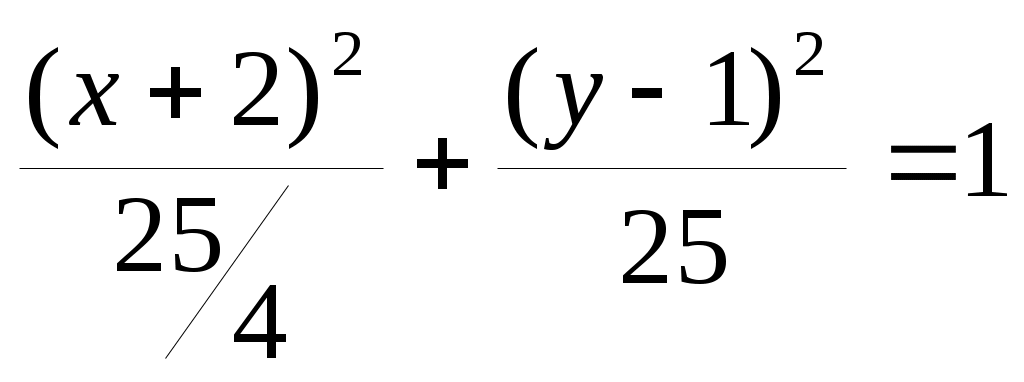 . .Выполним параллельный перенос осей координат по формулам 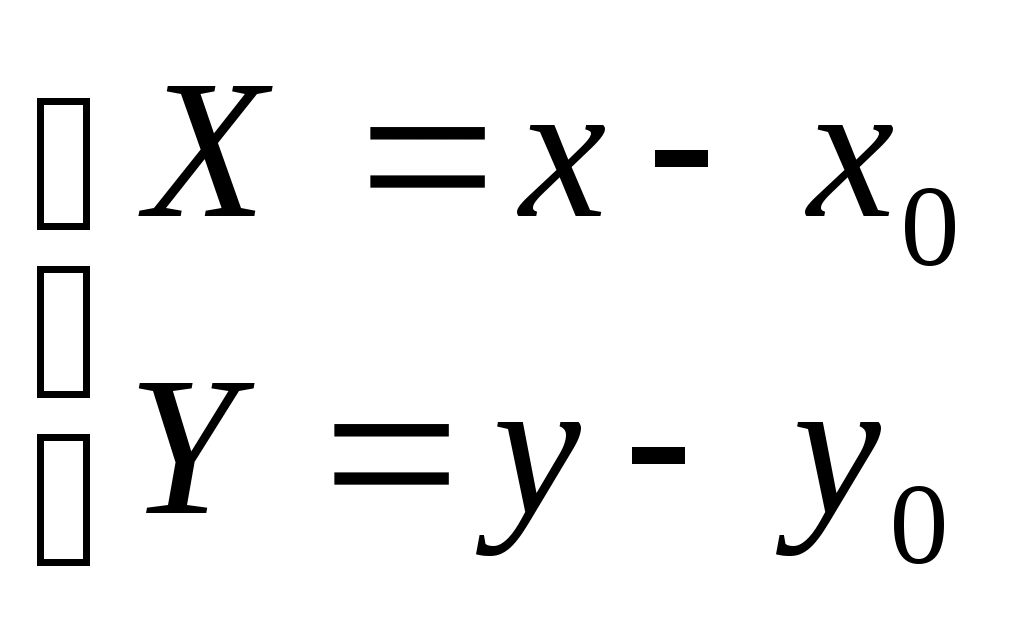 . При таком преобразовании начало координат переносится в точку . При таком преобразовании начало координат переносится в точку В нашем примере Итак, рассматриваемое уравнение определяет эллипс с центром в точке 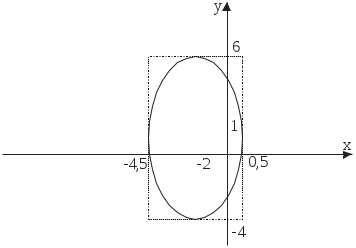 Рис. 13 Пример 2. Привести уравнение кривой второго порядка Решение. Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие координаты: В скобках выделим полный квадрат: Выполним замену переменных 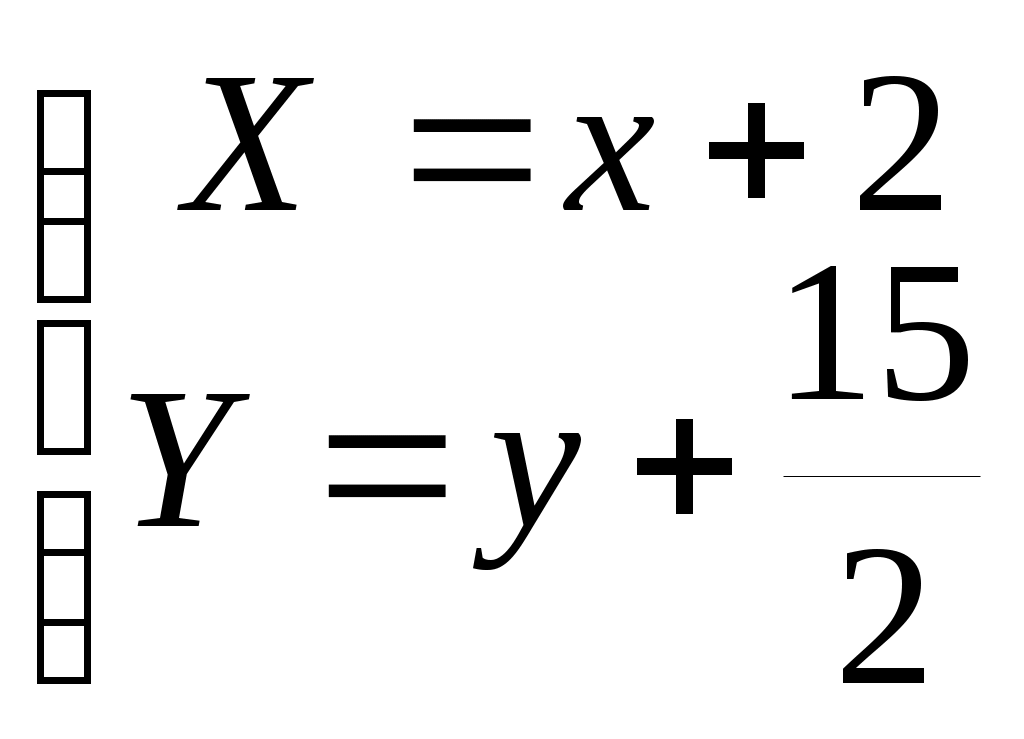 . После этого преобразования уравнение параболы принимает канонический вид . После этого преобразования уравнение параболы принимает канонический вид 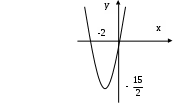 Рис. 14 Задача №4. Кривая задана в полярной системе координат уравнением Требуется: найти точки, лежащие на кривой, давая построить полученные точки; построить кривую, соединив построенные точки (от руки или с помощью лекала); составить уравнение этой кривой в прямоугольной декартовой системе координат. Решение. Сначала построим таблицу значений
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат 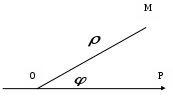 Рис. 15 Построим все точки, определенные в таблице и соединим их плавной линией  Рис. 16 Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат. Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами 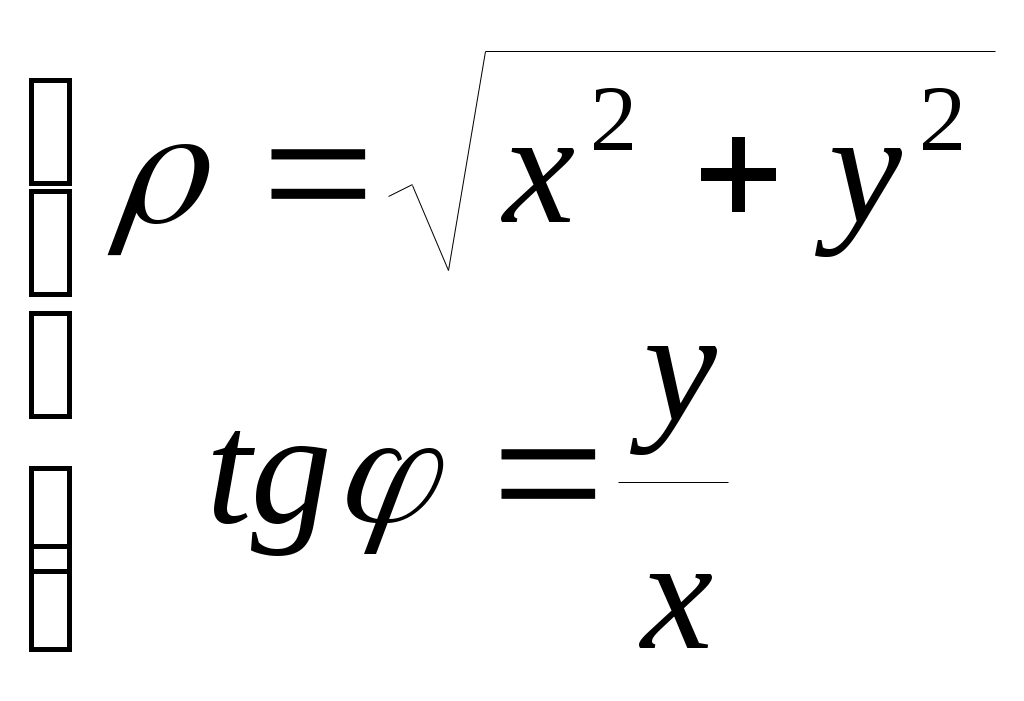 Откуда 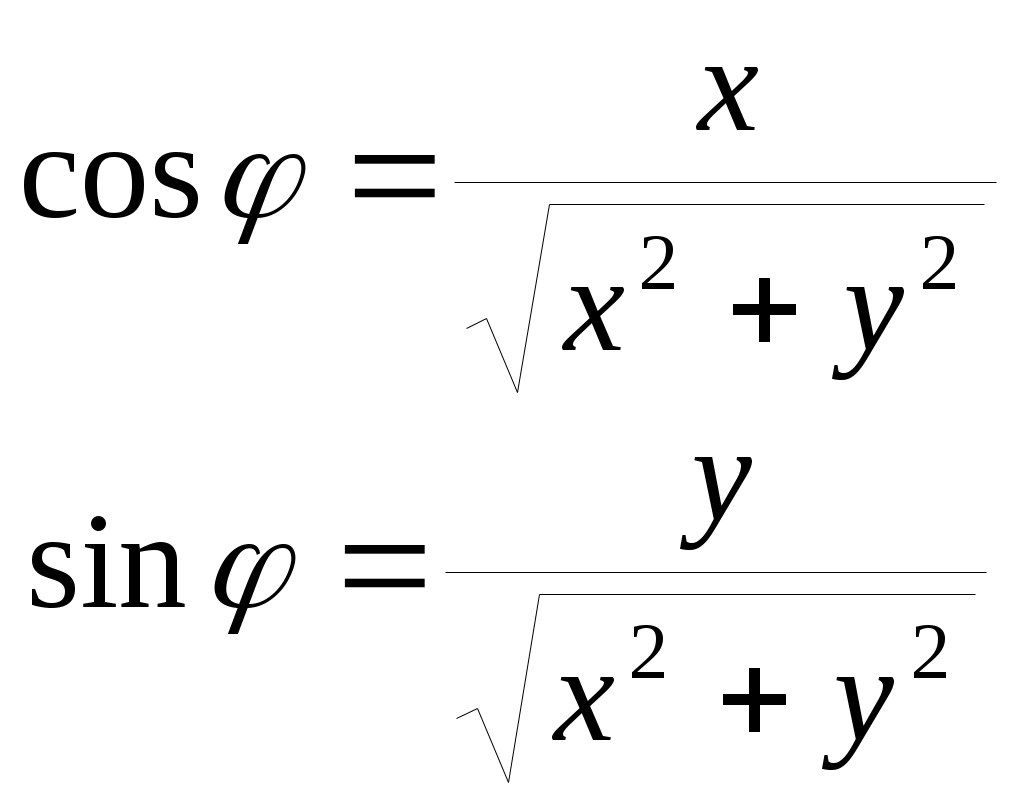 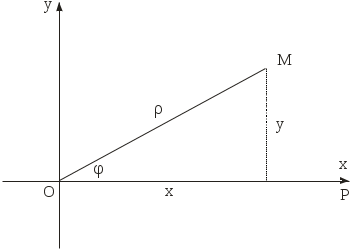 Рис. 17 Итак, в уравнении исходной кривой Задача №5. Построить на плоскости геометрическое место точек, определяемое неравенствами 1) 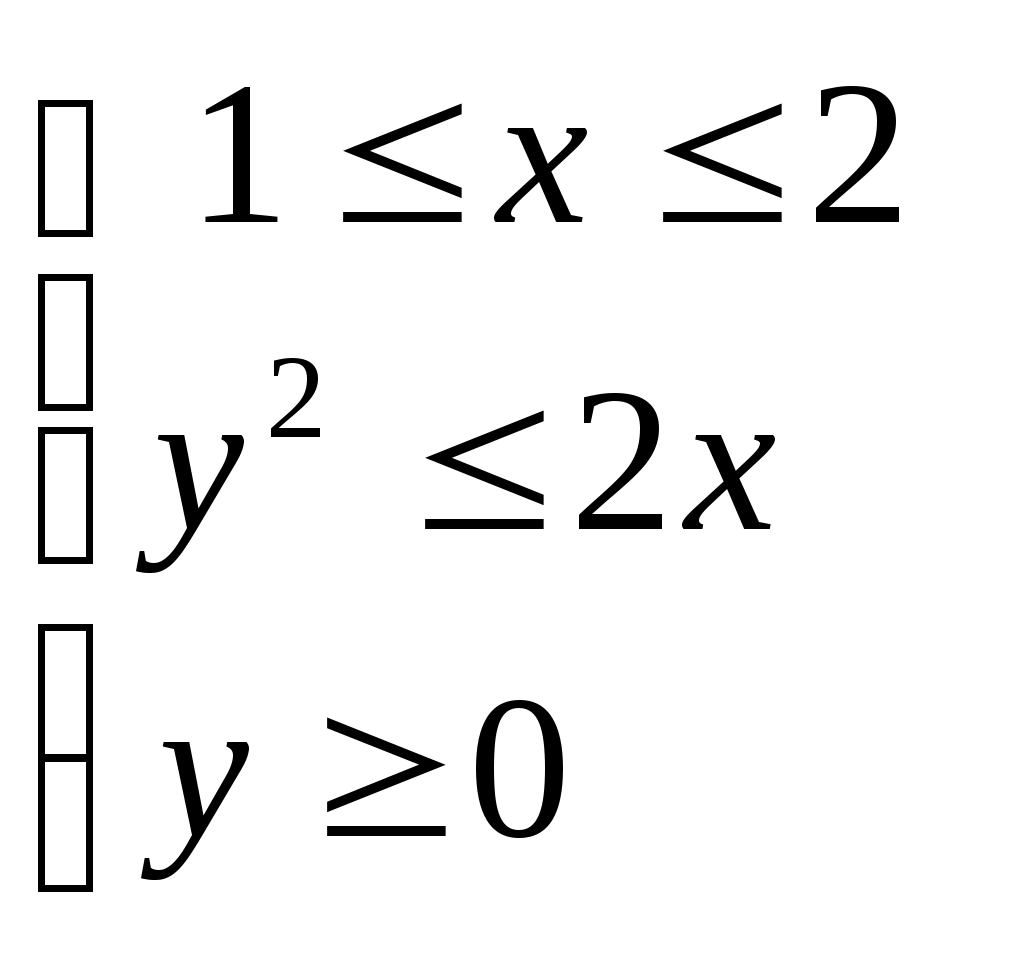 2) Решение. Для того, чтобы решить неравенство 1) Построим прямые 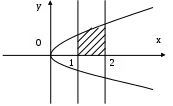 Рис. 18 2) Построим линию, определяемую уравнением 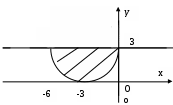 Рис. 19 |
