Контрольная работа №3 (1 курс 2 семестр) 20 вариант. Контрольная работа 3 Задание Вычислите определенные интегралы. 10. а б Решение.. б Решение
 Скачать 378.63 Kb. Скачать 378.63 Kb.
|
|
Контрольная работа №3 Задание 1. Вычислите определенные интегралы. 10. а) 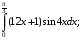 б) б) 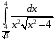 Решение. 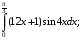 = =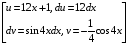 = =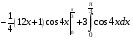 = == 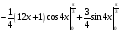 = =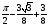 . .б) 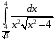 Решение. 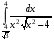 = =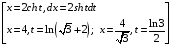 = =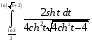 = == 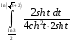 = =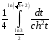 = =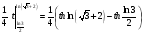 . .Задание 2. Вычислите площадь фигуры, ограниченной заданными линиями. Сделайте рисунок. 20. 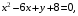 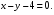 Построим область 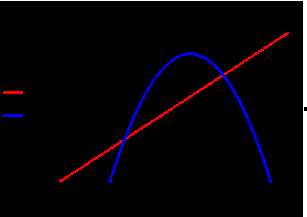 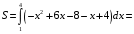 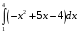 = =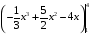 = == 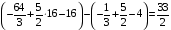 . .Ответ: 16,5 кв. ед. Задание 3. Найдите общие решения дифференциальных уравнений. 30. а) 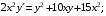 б) б) 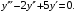 Решение. 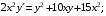 , , 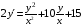 . .Подстановка 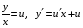 . .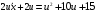 , , 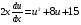 , , 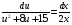 . .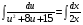 , , 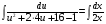 , , 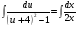 , ,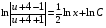 , , 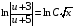 , , 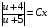 , ,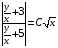 , , 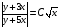 – общее решение дифференциального уравнения. – общее решение дифференциального уравнения.б) 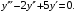 Решение. Составим хараетеристическое уравнение 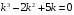 , , 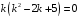 – корни характеристического уравнения: – корни характеристического уравнения: 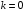 , , 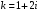 , , 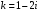 . .Общее решение дифференциального уравнения 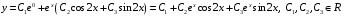 Задание 4. Решите задачу Коши при начальном условии 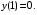 40. 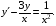 Решение. Подстановка: 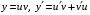 . .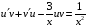 , , 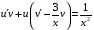 . .Пусть 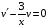 . .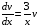 , , 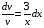 , , 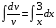 , , 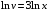 , , 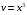 . .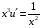 , , 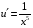 , , 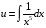 , , 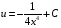 , ,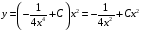 – общее решение. – общее решение.Решим задачу Коши 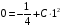 , , 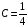 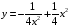 – частное решение. – частное решение.Задание 5. Вычислите объем тела, ограниченного указанными поверхностями, с помощью: 1) двойного интеграла; 2) тройного интеграла. 50. 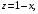 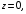 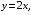 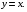 Решение. Проекция тела на плоскость хОу 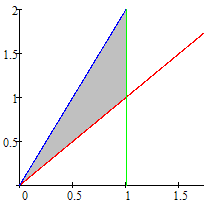 Определим объем тела: 1. 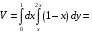 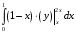 = =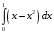 = == 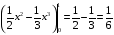 . .2. 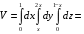 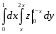 = =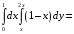 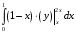 = == 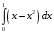 = =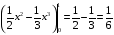 . .Ответ: 1/6 куб.ед. Задание 6. Даны векторное поле 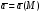 и две поверхности и две поверхности 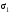 и и 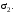 Вычислите: Вычислите:1) поток векторного поля 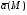 через замкнутую поверхность σ, ограниченную поверхностями через замкнутую поверхность σ, ограниченную поверхностями 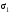 и и 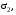 в направлении внешней нормали; в направлении внешней нормали;2) циркуляцию векторного поля 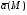 вдоль линии L пересечения поверхностей вдоль линии L пересечения поверхностей 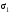 и и 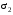 в положительном направлении обхода относительно орта в положительном направлении обхода относительно орта 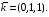 60. 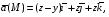 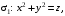 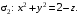 Решение. 1. Так как поверхность σ замкнута и нормаль внешняя, то для вычисления потока вектора 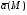 через эту поверхность воспользуемся формулой Гаусса-Остроградского. через эту поверхность воспользуемся формулой Гаусса-Остроградского.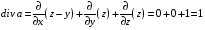 . .Поток равен. 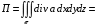 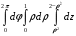 = = 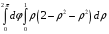 = == 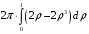 = = 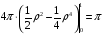 . .2. Найдем циркуляцию по формуле Стокса. 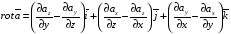 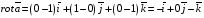 . .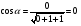 ; ; 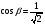 ; ; 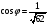 . .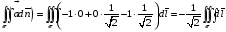 = =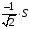 . .S – площадь проекции поверхностей 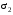 на плоскость на плоскость 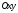 (окружность радиуса 1 с центром в начале координат). (окружность радиуса 1 с центром в начале координат). 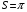 . .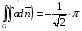 Контрольная работа №4 Задание 1. Исследуйте сходимость числового ряда. 70. 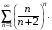 Решение. 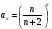 Найдем предел отношения 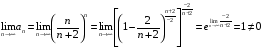 Следовательно, ряд расходится, так как не выполняется необходиный признак сходимасти 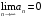 . .Задане 2. Найдите радиус и область сходимости степенного ряда, установите тип сходимости (абсолютная, условная сходимость). 80. 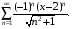 Решение. Рассмотрим ряд из модулей: 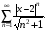 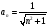 , , 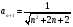 . .Найдем радиус сходимости 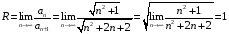 Область сходимости: 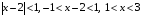 . .Иследуем сходимость ряда на концах интервала 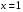 , , 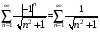 ряд расходится (по предельному признаку сраввнения, сравниваем с рядом ряд расходится (по предельному признаку сраввнения, сравниваем с рядом 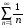 ). ).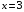 , , 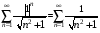 – расходится. – расходится.Исследуем ряд 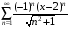 на концах интервала на концах интервала 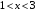 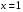 , , 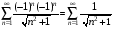 –расходится. –расходится.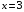 , , 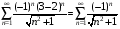 – знакочерезующийся ряд. – знакочерезующийся ряд.Воспольузуемся признаком Лейбница. 1-ое условие: 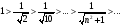 – выполняется. – выполняется.2-ое условие: 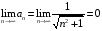 – выполняется. – выполняется.При 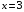 – ряд сходится. – ряд сходится.Область содимости: 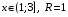 Задание 3. Вычислите определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена. 90. 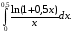 Решение. Разложим функцию в степенной ряд 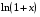 = = 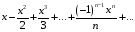 . .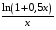 = = 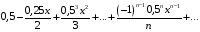 . .Тогда 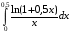 = = 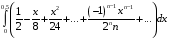 = == 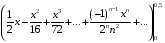 = = 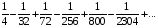 Для вычисления интеграла достаточно 5-ть первых членов ряда (6-ой член ряде не провосходит величины 0,001): 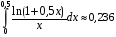 . . Задания 4. На промежутке 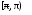 задана задана 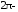 периодическая функция периодическая функция 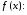 1) постройте график функции; 2) разложите функцию в ряд Фурье; 3) постройте график суммы ряда Фурье. 100. 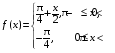 Решение. 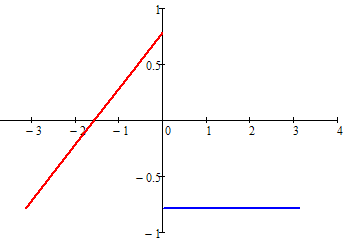 Разложим функцию в ряд Фурье 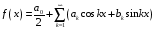 , ,где 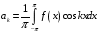 , , 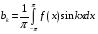 . .Вычислим коэффициенты ряда Фурье 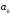 , , 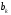 . .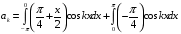 = = 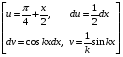 = == 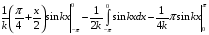 = = 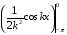 = = 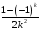 = == 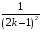 . .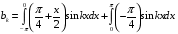 = = 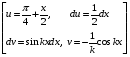 = = = 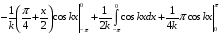 = = 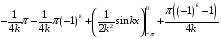 = = 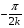 . .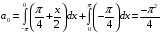 Тогда разложение функции в ряд Фурье имеет вид: 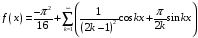 . .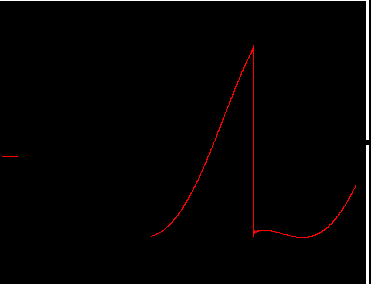 Задание 5. Разложите функцию 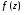 в ряд Лорана в окрестности точки в ряд Лорана в окрестности точки 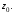 110. 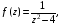 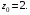 Решение. 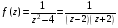 . .Функция f(z) имеет в точке z = 2 полюс первого порядка, поэтому можно избавиться от этой особенности умножением этой функции на z – 2. Полученную таким образом функцию g(z) = (z – 2) f(z) мы разложим в ряд Тейлора по степеням z – 2. 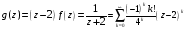 . .Тогда 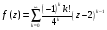 Задание 6. Вычислите заданный интеграл при помощи вычетов. 120. 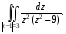 Решение. Контур интегрирования представляет собой окружность радиуса 3 с центром в точке 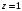 . .Внутри контура находятся две изолированные особые точки подынтегральной функции 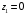 и и 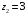 – простые полюса. – простые полюса.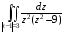 = =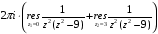 . .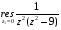 = =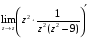 = =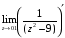 = =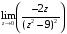 = 0. = 0.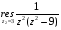 = =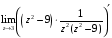 = =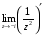 = =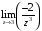 = =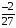 . .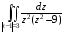 = = 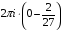 = = 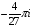 . .Задание 7. Найдите изображение заданного оригинала 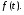 130. 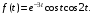 Решение. 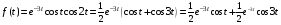 . .По таблице изображений находим. 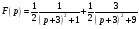 |
