Главная страница
Навигация по странице:

  • Сумма 15,378

    		•

    Контрольная работа 4 Задача Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города


    Скачать 334 Kb.
    НазваниеКонтрольная работа 4 Задача Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города
    Анкор4.doc
    Дата19.12.2017
    Размер334 Kb.
    Формат файлаdoc
    Имя файла4.doc
    ТипКонтрольная работа
    #12196

    powerpluswatermarkobject3


    Вариант 6

    Контрольная работа №4

    Задача 1. Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города.



    Размер вклада, тыс. руб.
    До 40
    40–60
    60–80
    80–100
    Свыше 100
    Итого:

    Число вкладов
    32
    56
    92
    120
    100
    400


    Найти:

    а) вероятность того, что средний размер вклада в Сбербанке отличается от среднего размера вклада в выборке не более чем на 5 тыс. руб. (по абсолютной величине);

    б) границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб.;

    в) объем повторной выборки, при которой те же границы для доли вкладов, полученные в пункте б), можно гарантировать с вероятностью 0,9876;

    дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
    Решение. Вычислим сначала числовые характеристики выборки. Построим соответствующий простой вариационный ряд, выбрав в качестве вариант середины интервалов:


     
    30
    50
    70
    90
    110
    Итого

     
    32
    56
    92
    120
    100
    400


    Найдем среднее:


    Найдем исправленную дисперсию:

    .
    Найдем исправленное среднеквадратичное отклонение: .

    Расчеты в таблице ниже:


     
    30
    50
    70
    90
    110
    Сумма

     
    32
    56
    92
    120
    100
    400

     
    960
    2800
    6440
    10800
    11000
    32000

     
    80000
    50400
    9200
    12000
    90000
    241600


    а) Найдем вероятность того, что средний размер вклада в Сбербанке отличается от среднего размера вклада в выборке не более чем на 5 тыс. руб. (по абсолютной величине), то есть что предельная ошибка выборки равна 5.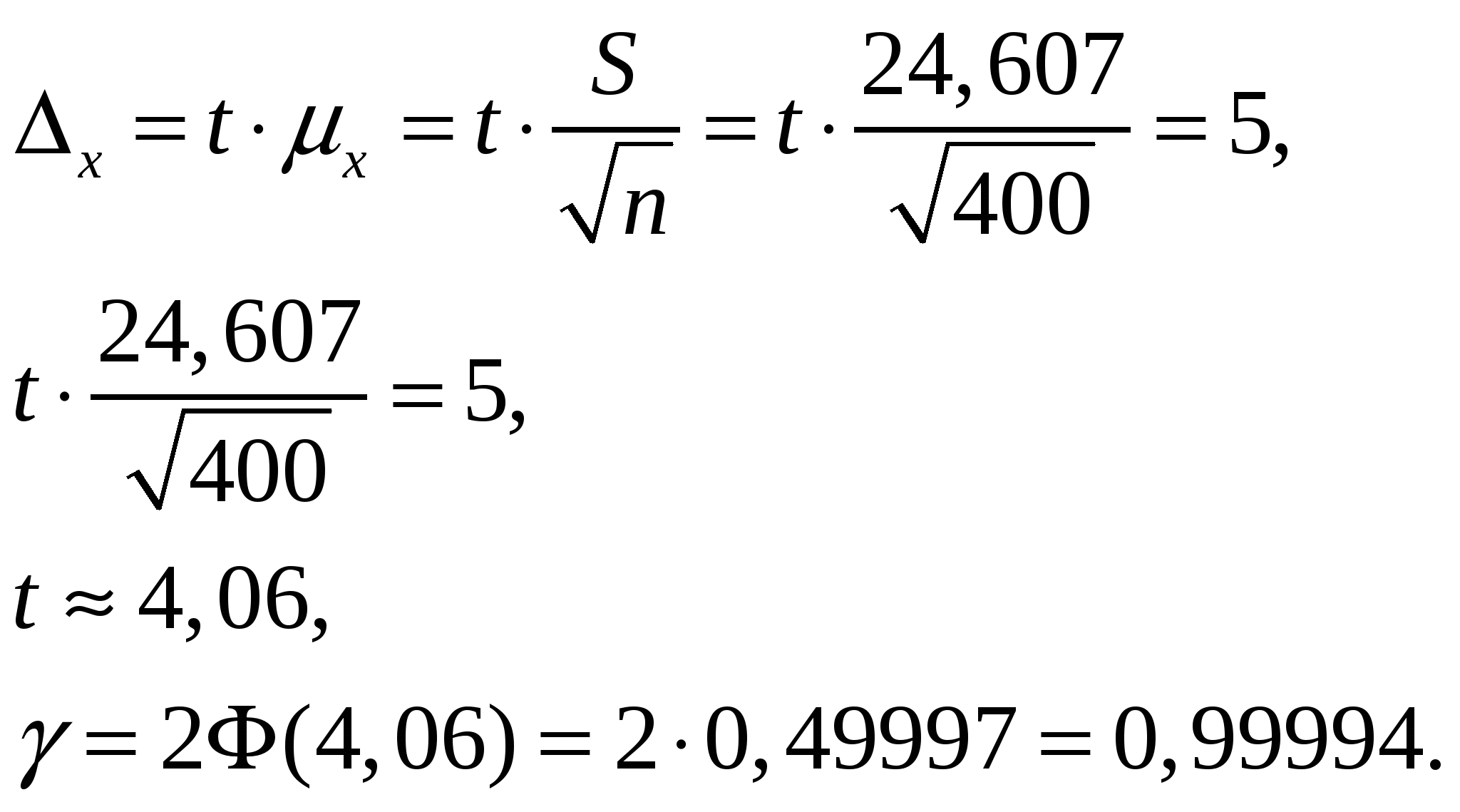



    Вероятность 0,99994 или 99,994%.

    б) Найдем границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб.
    Выборочная доля вкладов, размер которых менее 60 тыс. руб. равна .

    Предельная ошибка для доли. Коэффициент .

    Получаем:



    Тогда границы для доли всех вкладов размером менее 60 тыс. руб. имеют вид: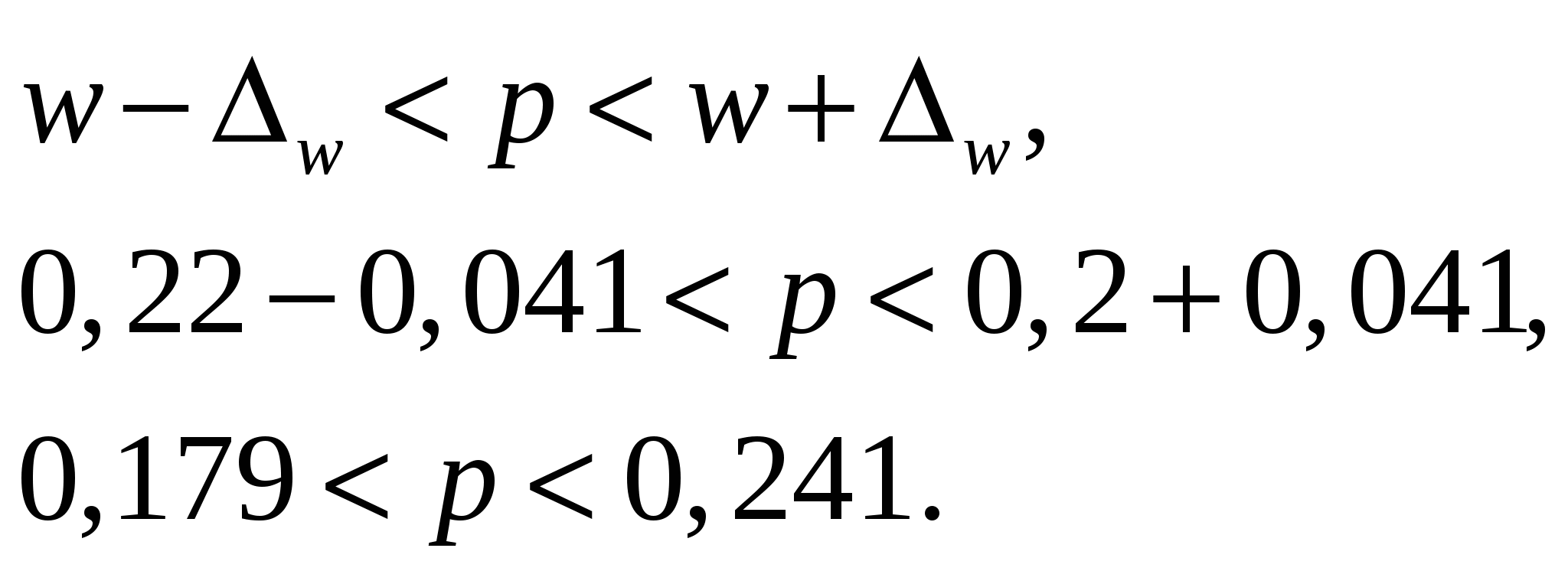



    От 17,9% до 24,1% всех вкладов.
    в) Найдем объем выборки, при которой те же границы для доли вкладов, полученные в пункте б), можно гарантировать с вероятностью 0,9876.
    Нужно найти объем выборки , при котором предельная ошибка будет также равна Формула для объема выборки имеет вид: .

    Коэффициент . Подставляем все данные:

    .
    Дадим ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет. Тогда рекомендуется брать . Получаем:

    .

    Задача 2. По данным задачи 1, используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – размер вклада в Сбербанке – распределена по нормальному закону.

    Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
    Решение. Пронормируем случайную величину , то есть перейдем к величине , вычислим концы интервалов по формулам , .
    Вычислим теоретические (выравнивающие частоты) , где , - вероятность попадания в интервал , - функция Лапласа. Для нахождения значений составим расчетную таблицу:



     
     
     
     
     
     
     




     до 40
    40
    32
     
    -1,626
    -0,5
    -0,448
    0,052
    20,809

    40
    60
    56
    -1,626
    -0,813
    -0,448
    -0,292
    0,1562
    62,460

    60
    80
    92
    -0,813
    0
    -0,292
    0
    0,2918
    116,730

    80
    100
    120
    0
    0,8128
    0
    0,2918
    0,2918
    116,730

    100
    более 100 
    100
    0,8128
     
    0,2918
    0,5
    0,2082
    83,270

















































    Сумма
    15,378


    Сравним эмпирические и теоретические частоты, используя критерий Пирсона:

    .

    По таблице критических точек распределения по уровню значимости и числу степеней свободы k = 5 - 3 = 2, находим кр. = 6,0. Так как набл. = 15,378 > кр. = 6,0, то следует отвергнуть гипотезу о нормальном распределении данной величины.
    Построим теоретическую нормальную кривую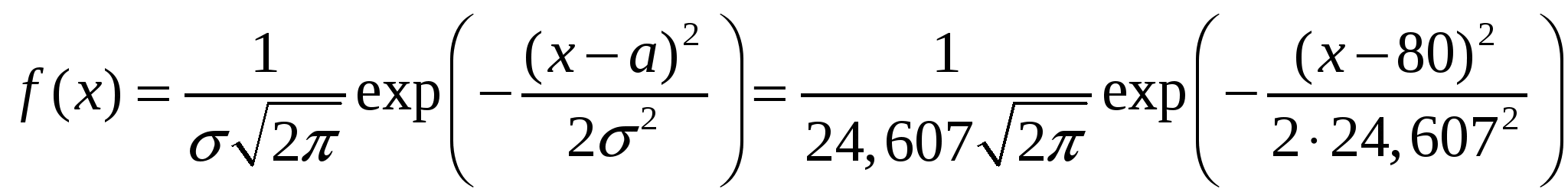



    и гистограмму на одном чертеже.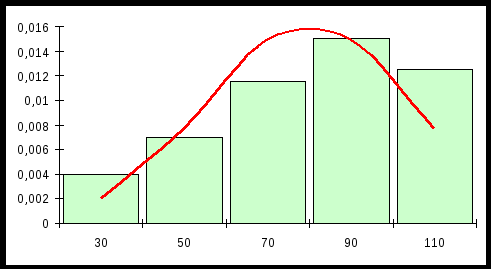


    Расчетная таблица:


     
    30
    50
    70
    90
    110

     
    32
    56
    92
    120
    100

    плотность отн. частот 
    0,004
    0,007
    0,0115
    0,015
    0,0125

     теорет. плотность

    0,0021
    0,0077
    0,0149
    0,0149
    0,0077


    Задача 3. Распределение 110 предприятий по стоимости основных производственных фондов X (млн. руб.) и стоимости произведенной продукции Y (млн. руб.) представлены в таблице: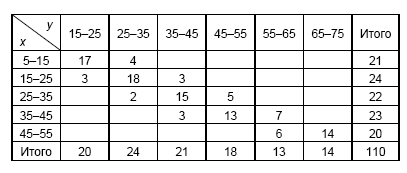


    Необходимо:

    1) вычислить групповые средние и построить эмпирические линии регрессии;

    2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость:

    а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

    б) вычислить коэффициент корреляции; на уровне значимости a = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;

    в) используя соответствующее уравнение регрессии, определить среднюю стоимость произведенной продукции, если стоимость основных производственных фондов составляет 45 млн. руб.

    Решение. Составим корреляционную таблицу, в качестве вариант выберем середины интервалов.


     
    20
    30
    40
    50
    60
    70
     

    10
    17
    4
     
     
     
     
    21

    20
    3
    18
    3
     
     
     
    24

    30
     
    2
    15
    5
     
     
    22

    40
     
     
    3
    13
    7
     
    23

    50
     
     
     
     
    6
    14
    20

     
    20
    24
    21
    18
    13
    14
    110


    1) Найдем групповые средние по формулам: ; .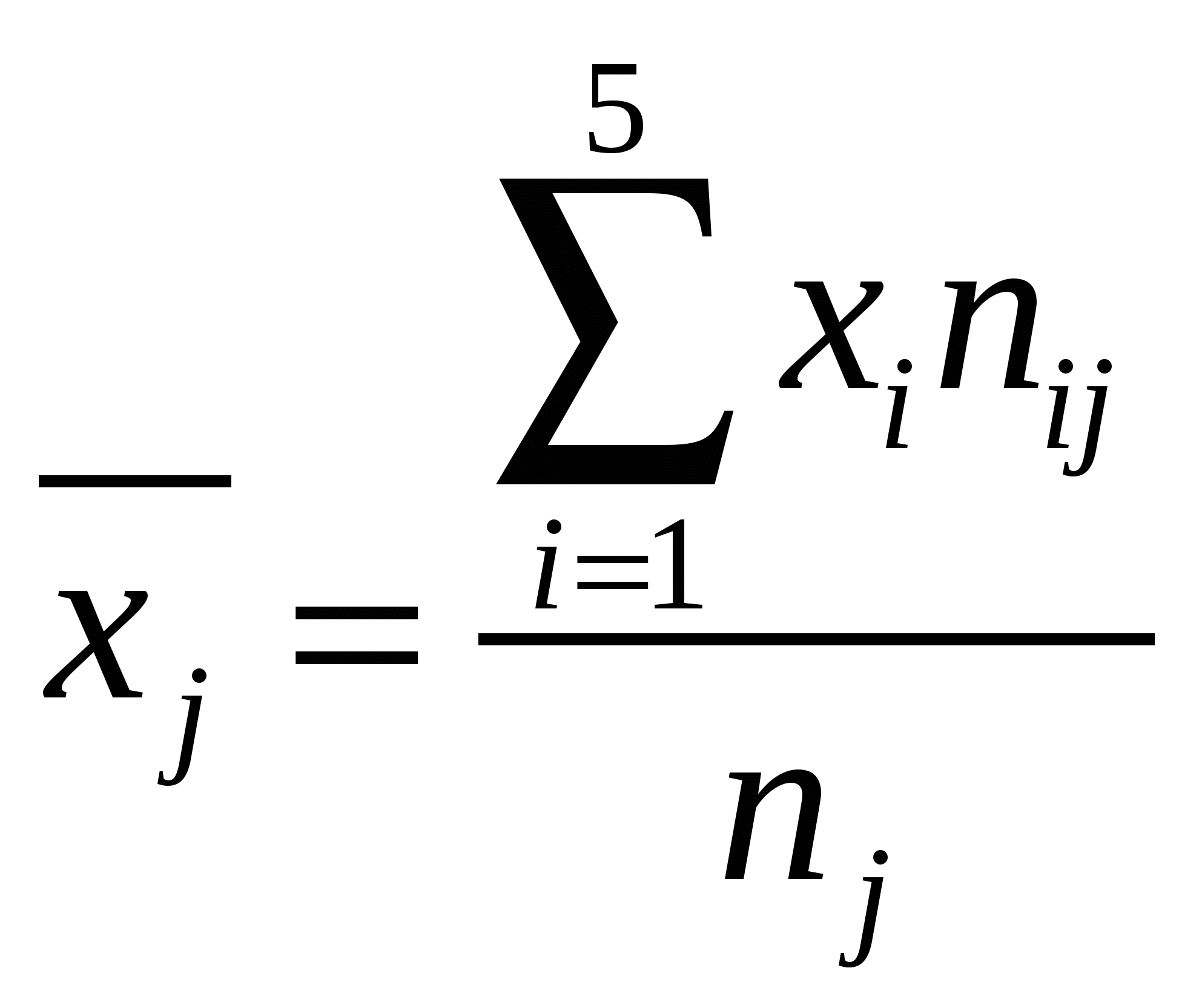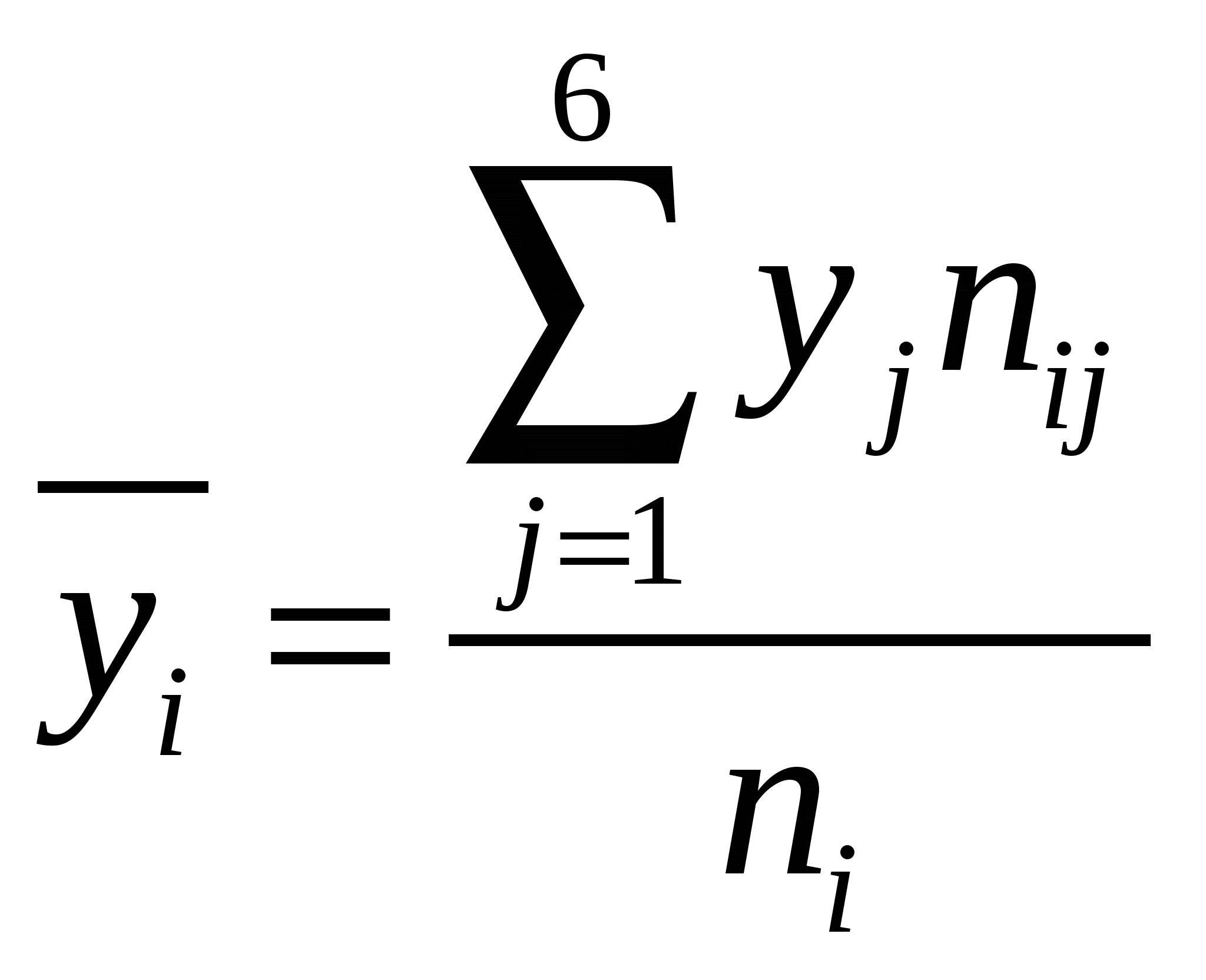

    Вычисления проведем в Excel, получаем:



    11,5
    19,17
    30
    37,22
    44,62
    50



    20
    30
    40
    50
    60
    70








    10
    21,905

    20
    30,000

    30
    41,364

    40
    51,739

    50
    67,000


    Построим эмпирические линии регрессии ( 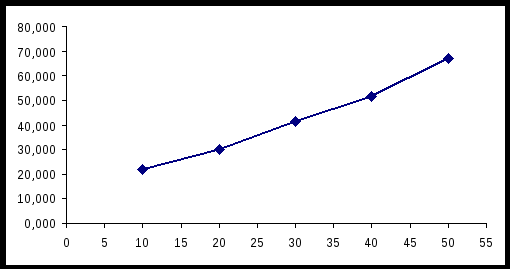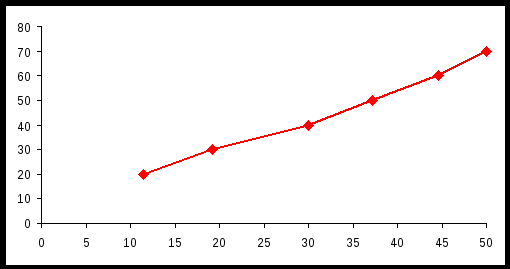на , на ).



    Из вида эмпирических линий регрессии можно заключить, что между переменными наблюдается линейная зависимость.
    Найдем уравнения прямых линий регрессии. Вычислим необходимые величины (расчеты в таблицах ниже):
    10
    20
    30
    40
    50
    Сумма



    21
    24
    22
    23
    20
    110



    210
    480
    660
    920
    1000
    3270

     
    2100
    9600
    19800
    36800
    50000
    118300






    20
    30
    40
    50
    60
    70
    Сумма



    20
    24
    21
    18
    13
    14
    110



    400
    720
    840
    900
    780
    980
    4620

     
    8000
    21600
    33600
    45000
    46800
    68600
    223600


    , ,

    ,


    , ,

    ,

    .

    = 160900






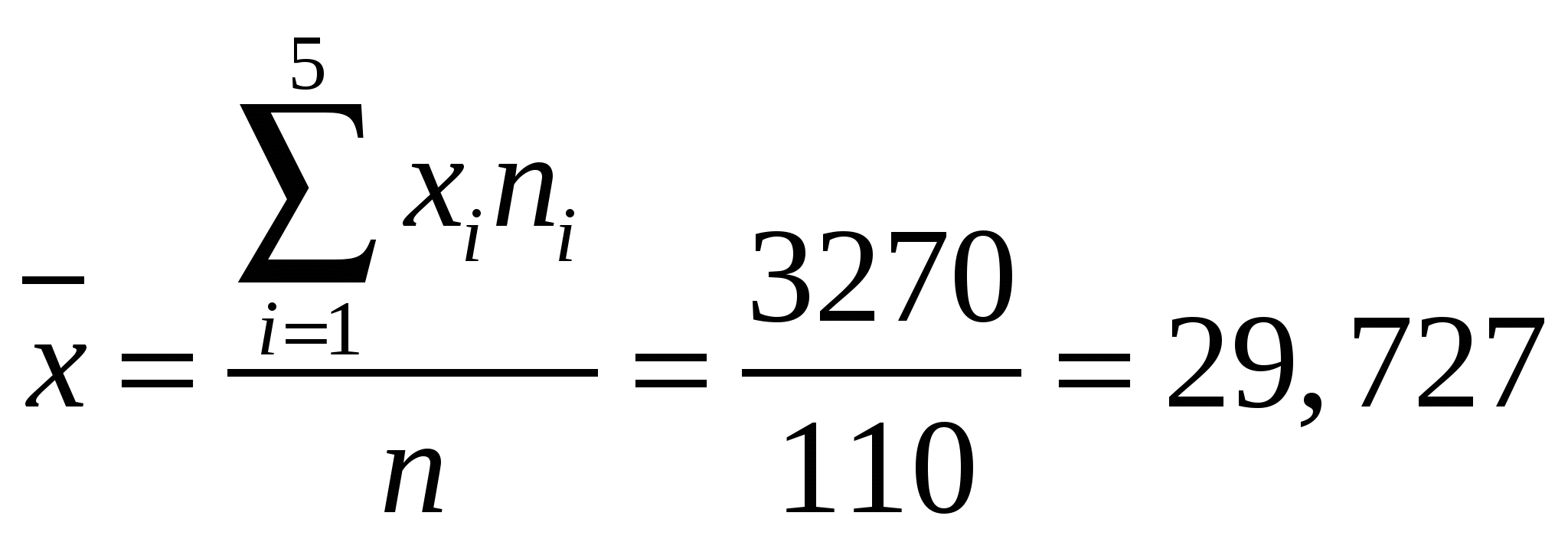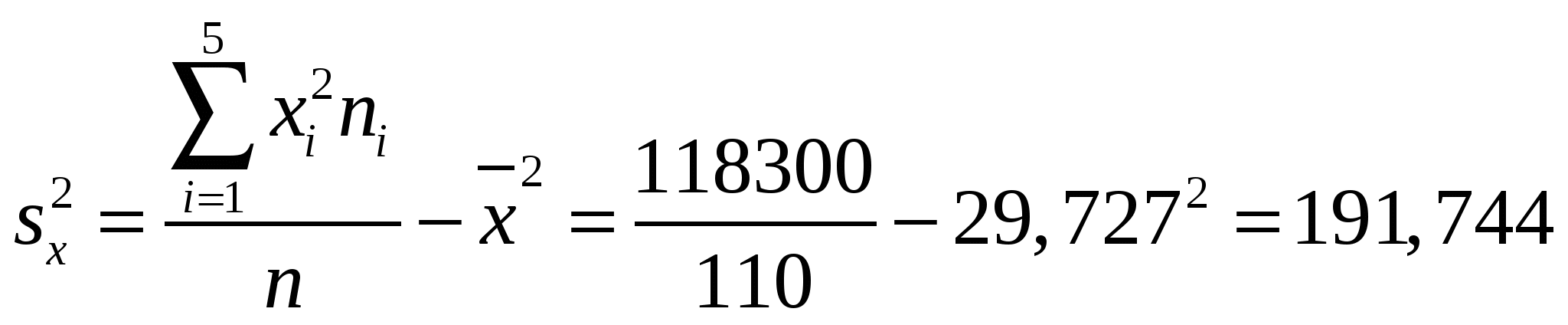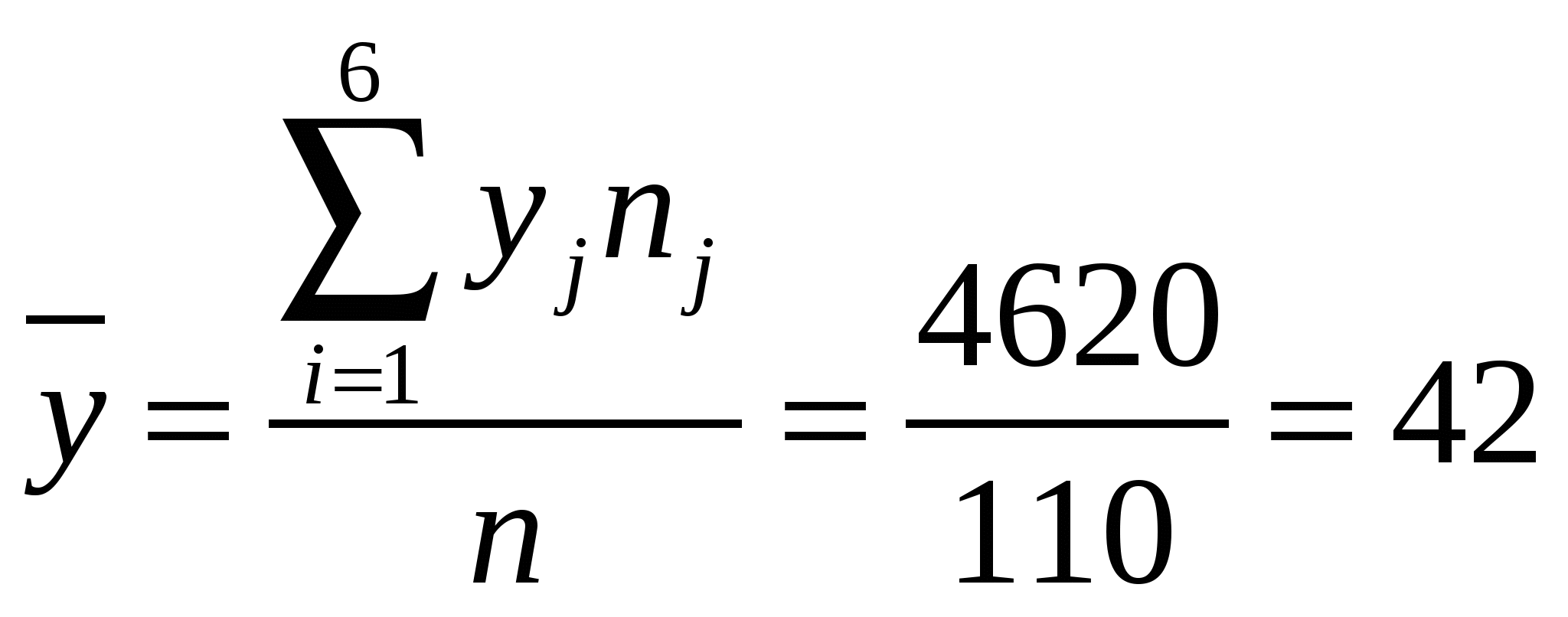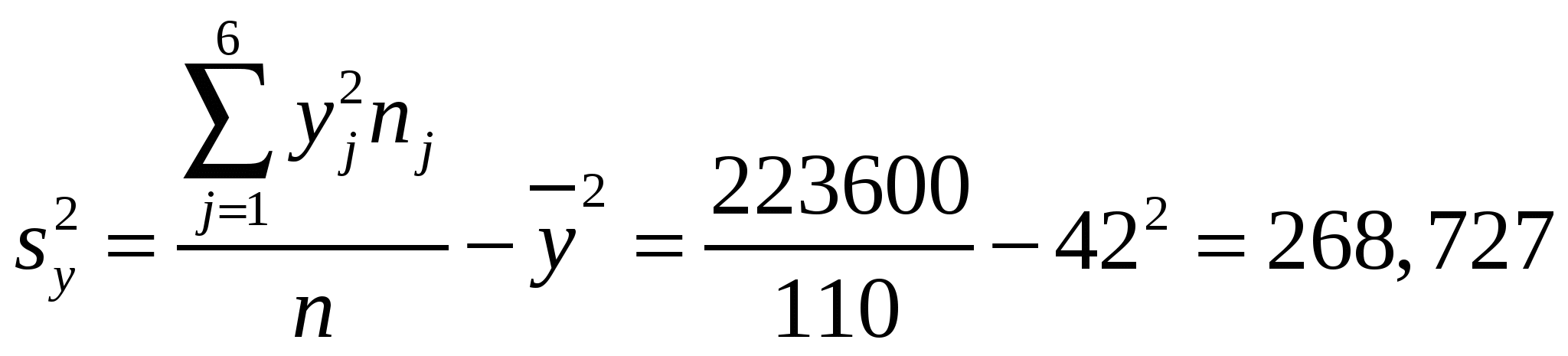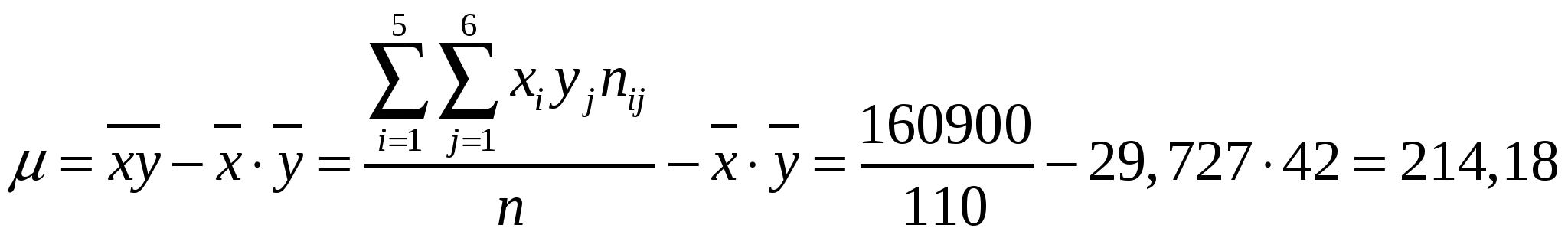    Уравнения прямых регрессии: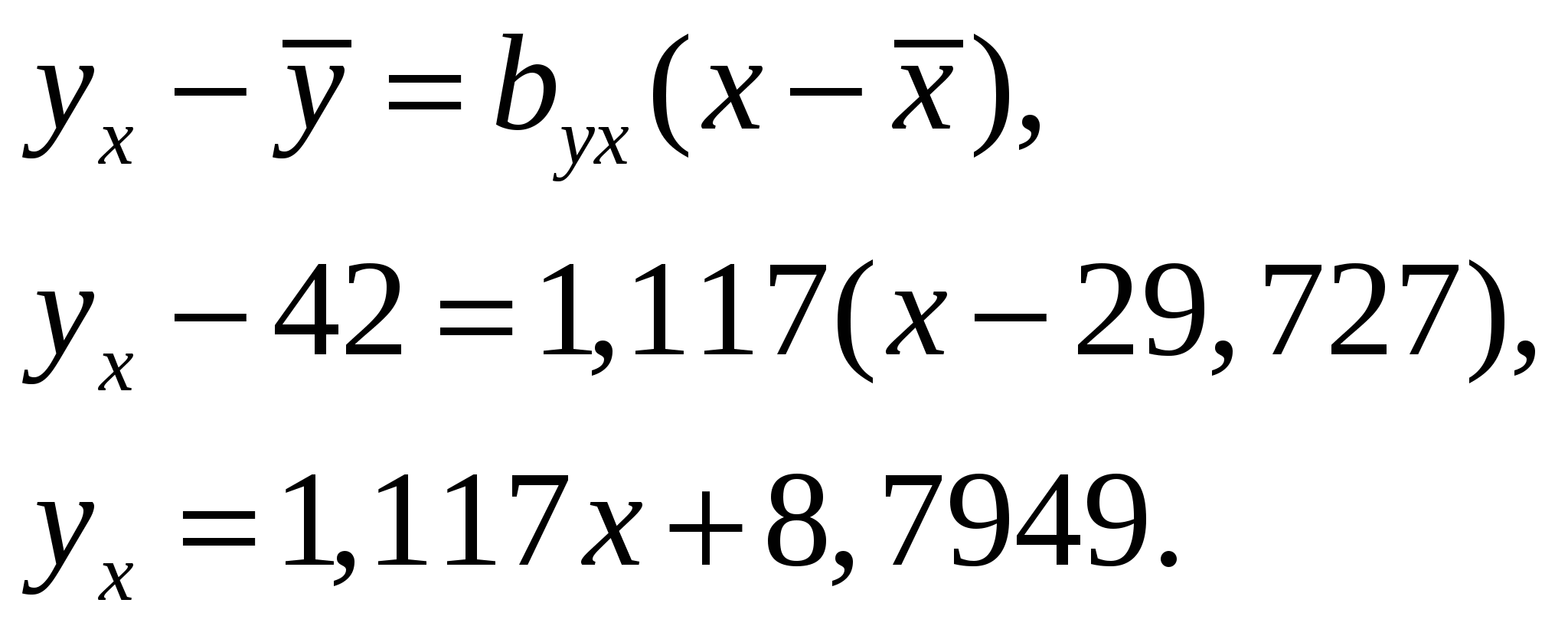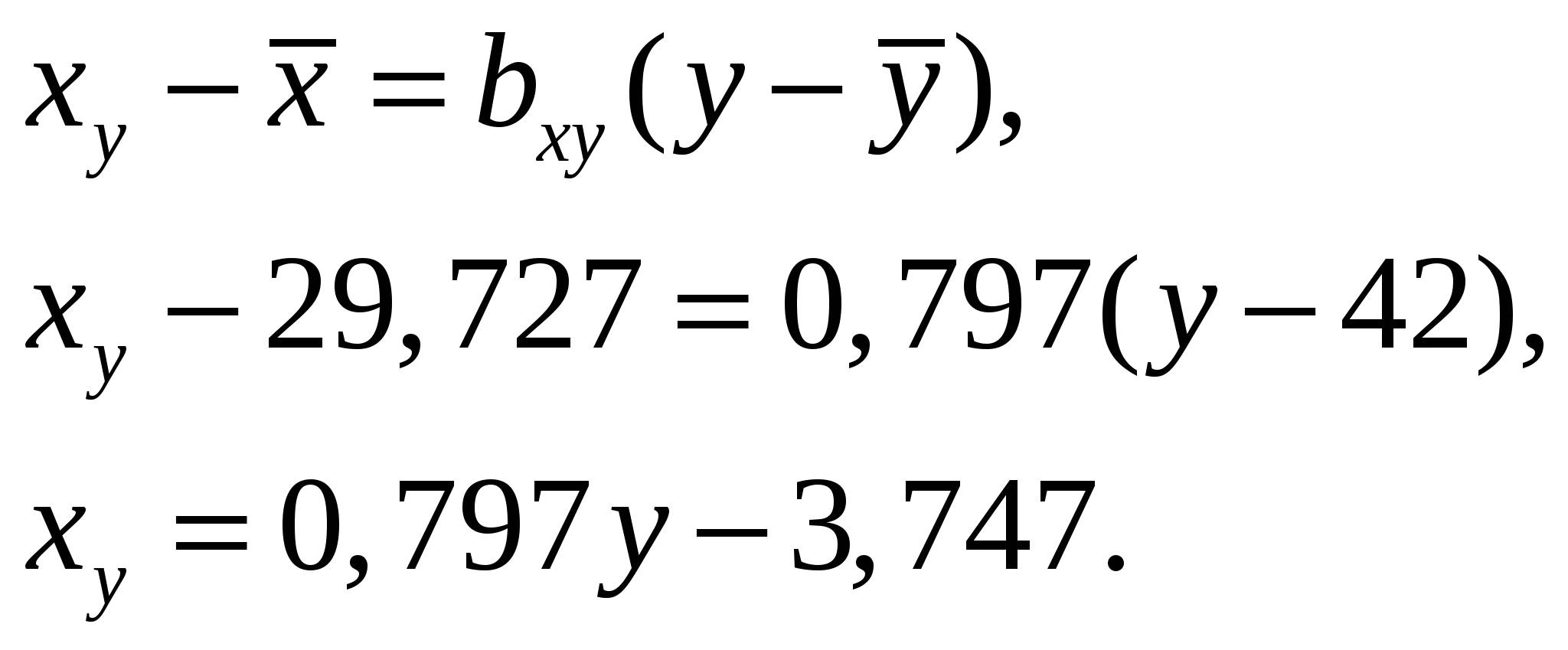



    Построим графики линий регрессии на одном чертеже с эмпирическими линиями регрессии.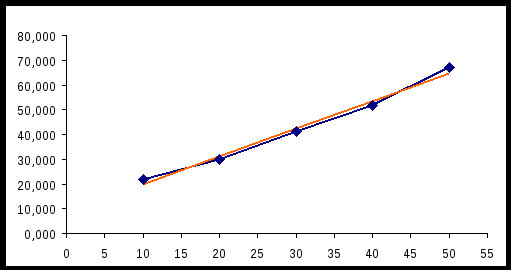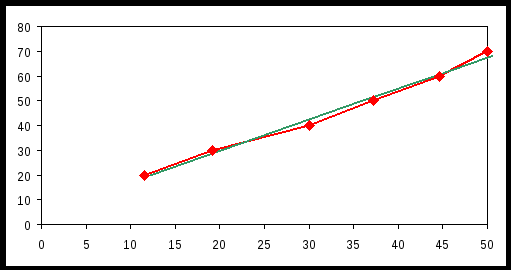



    Экономическая интерпретация полученных уравнений:

    - при увеличении стоимости основных производственных фондов на 1 млн. руб., стоимость произведенной продукции растет в среднем на 1,117 млн. руб.

    - при увеличении стоимости произведенной продукции на 1 млн. руб., стоимость основных производственных фондов растет в среднем на 0,797 млн. руб.
    Вычислим коэффициент корреляции
    На уровне значимости 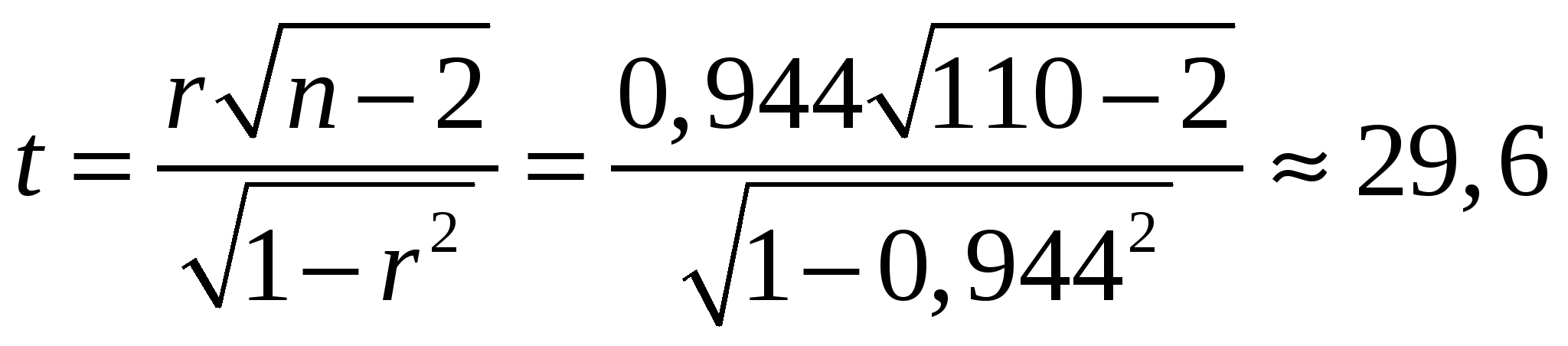оценим значимость коэффициента корреляции. Вычислим значение критерия

    По таблице критерия Стьюдента для уровня значимости 0,05 находим . Так как наблюдаемое значение 29,6 больше критического, коэффициент корреляции значим.
    Связь между переменными и тесная, прямая.
    Используя соответствующее уравнение регрессии, определим среднюю стоимость произведенной продукции, если стоимость основных производственных фондов составляет 45 млн. руб.:

    млн. руб.
    Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru ID работы: 27574

    Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru ID работы: 27574

    написать администратору сайта