КрВар1. Контрольная работа 5. Найти общий интеграл дифференциального уравнения.. Решение
 Скачать 433 Kb.
|
|
Контрольная работа №5. 1. Найти общий интеграл дифференциального уравнения. 1.  .Решение. Имеем дифференциальное уравнение 1-го порядка с разделяющимися переменными.  Разделим переменные и проинтегрируем обе части уравнения: 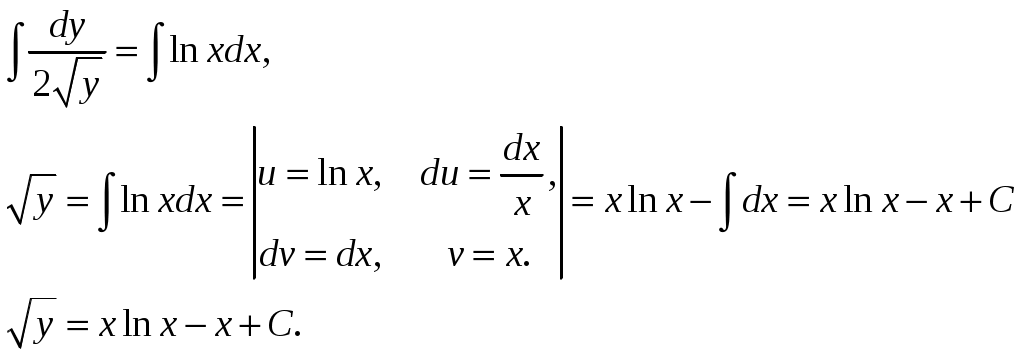  Общее решение дифференциального уравнения имеет вид:  .Ответ: 2. Найти общий интеграл дифференциального уравнения. 11.  .Решение. Это линейное дифференциальное уравнение первого порядка. Будем искать решение в виде  , тогда  . После подстановки и выражения для производной в уравнение получим . .Получаем систему: 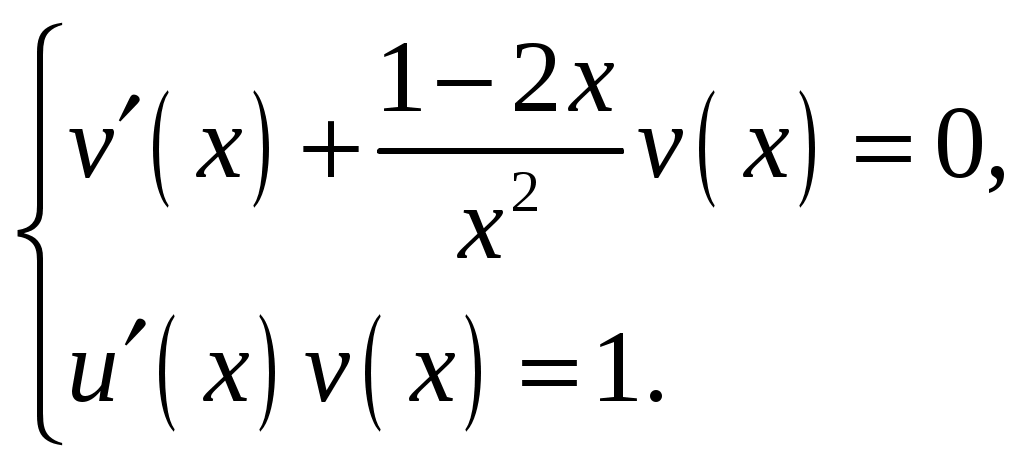 Решим уравнение  .Получаем:  . . .откуда при C =0:  и искомая функция будет иметь вид: .После подстановки функции 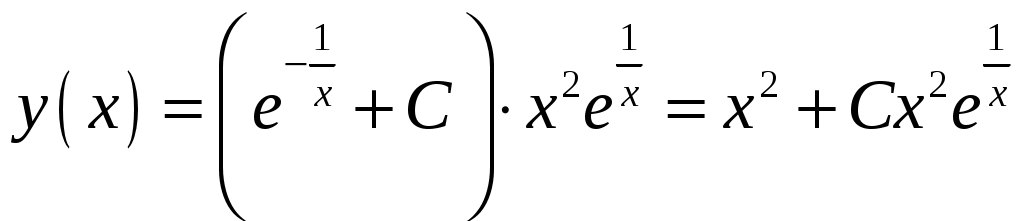во второе уравнение, получим . Решим последнее уравнение: , Тогда  – общее решение исходного уравнения.Ответ:  .3. Найти частные решения дифференциального уравнения, удовлетворяющие условиям: 21.  , а)  .б)  Решение. Имеем дифференциальное уравнение второго порядка, которое не содержит  Интегрируем дважды: 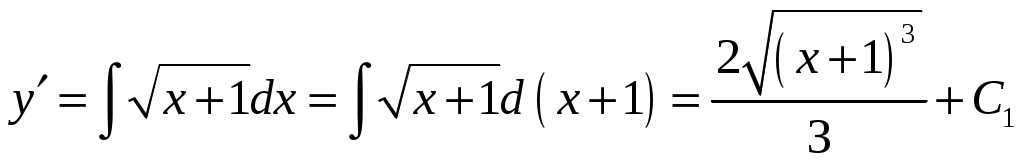 . 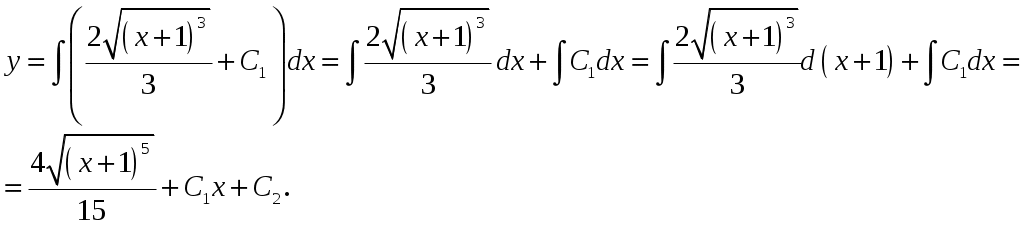Тогда: 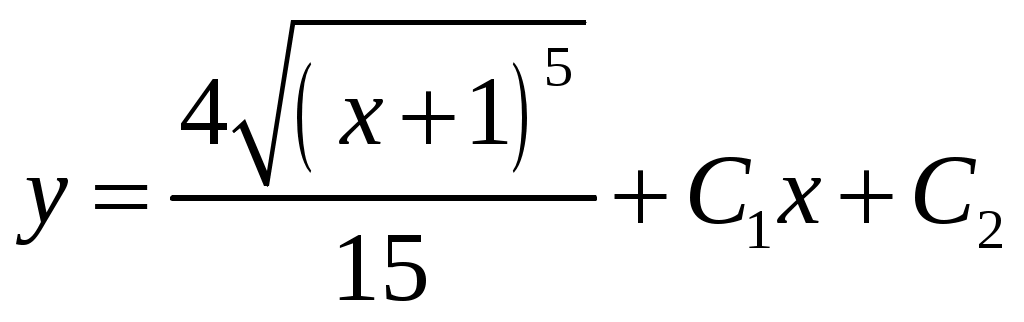 –общее решение исходного дифференциального уравнения.а) Ищем частное решение: 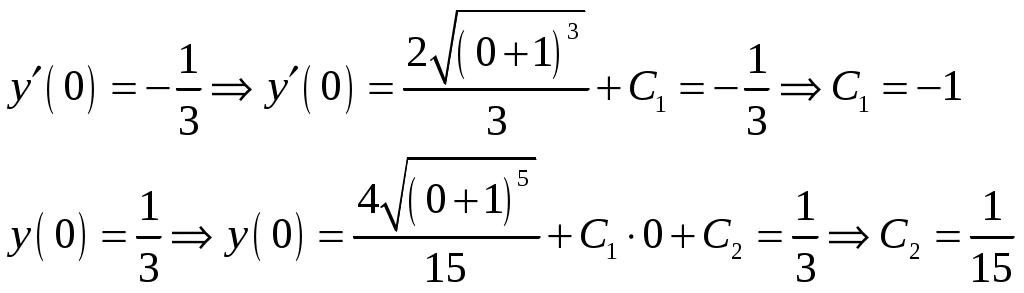. .Таким образом, решение задачи Коши: 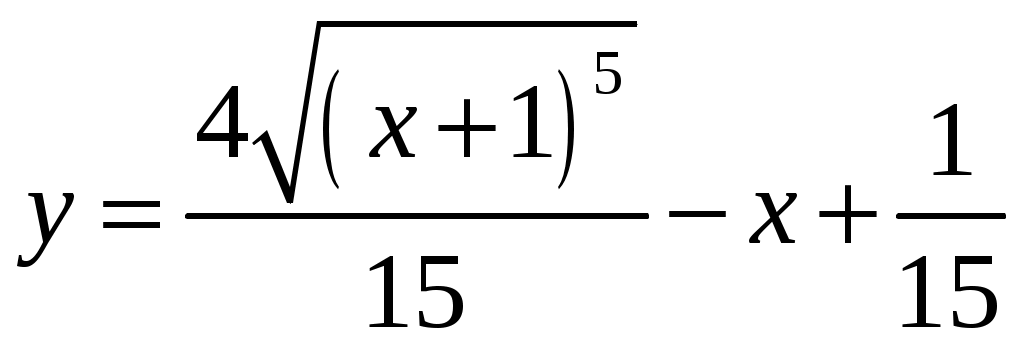 .б) Ищем частное решение: 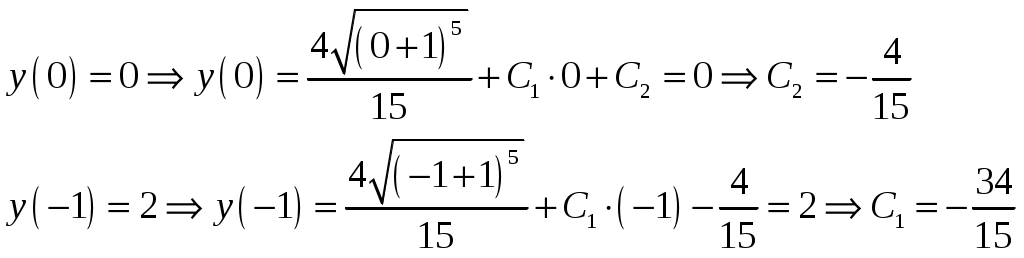. .Таким образом, решение задачи Коши: 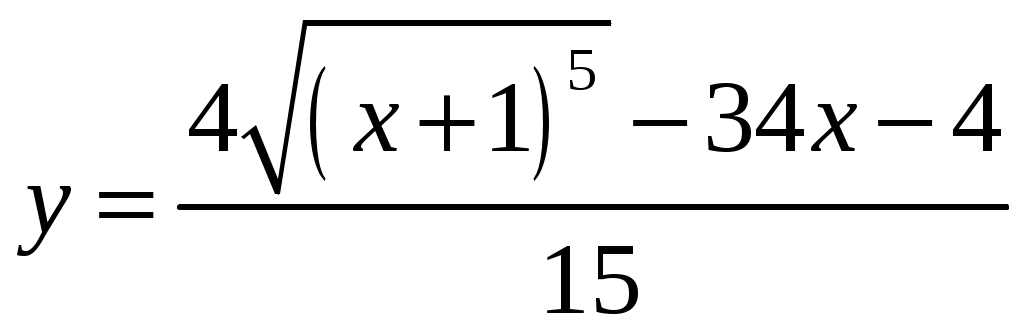 .4. Найти общее решение дифференциального уравнения: 31.  .Решение. Имеем линейное однородное дифференциальное уравнение четвертого порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение 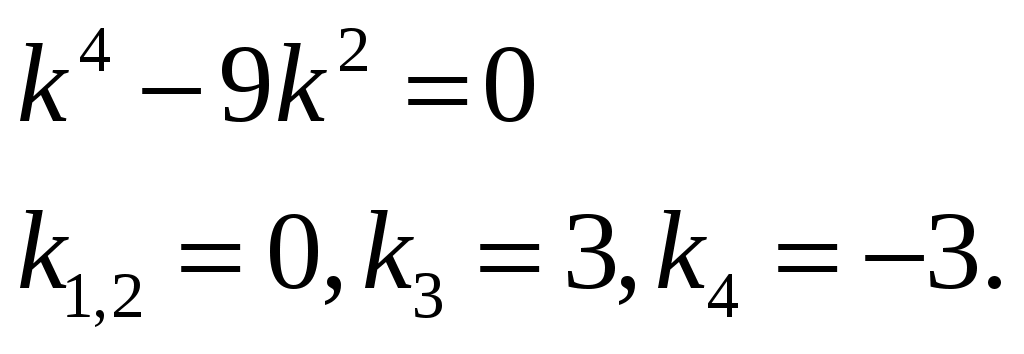 Так как корни характеристического уравнения действительные равные и действительные разные числа, то общее решение  будет иметь вид .Ответ: .5. Найти общее решение дифференциального уравнения: 41.  .Решение. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:  , где  – общее решение соответствующего однородного уравнения, – частное решение исходного неоднородного уравнения.1) Найдем – общее решение соответствующего однородного уравнения, т.е. уравнения: Для этого составляем характеристическое уравнение:  Получаем:  . Эти корни являются действительными разными, поэтому система решений, соответствующая этим корням, будет иметь вид: .2) Найдем – частное решение исходного неоднородного уравнения в виде:  Находим:   .Подставляем в исходное уравнение:   .  .Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:  Ответ: 6. Найти общее решение системы дифференциальных уравнений: 51. 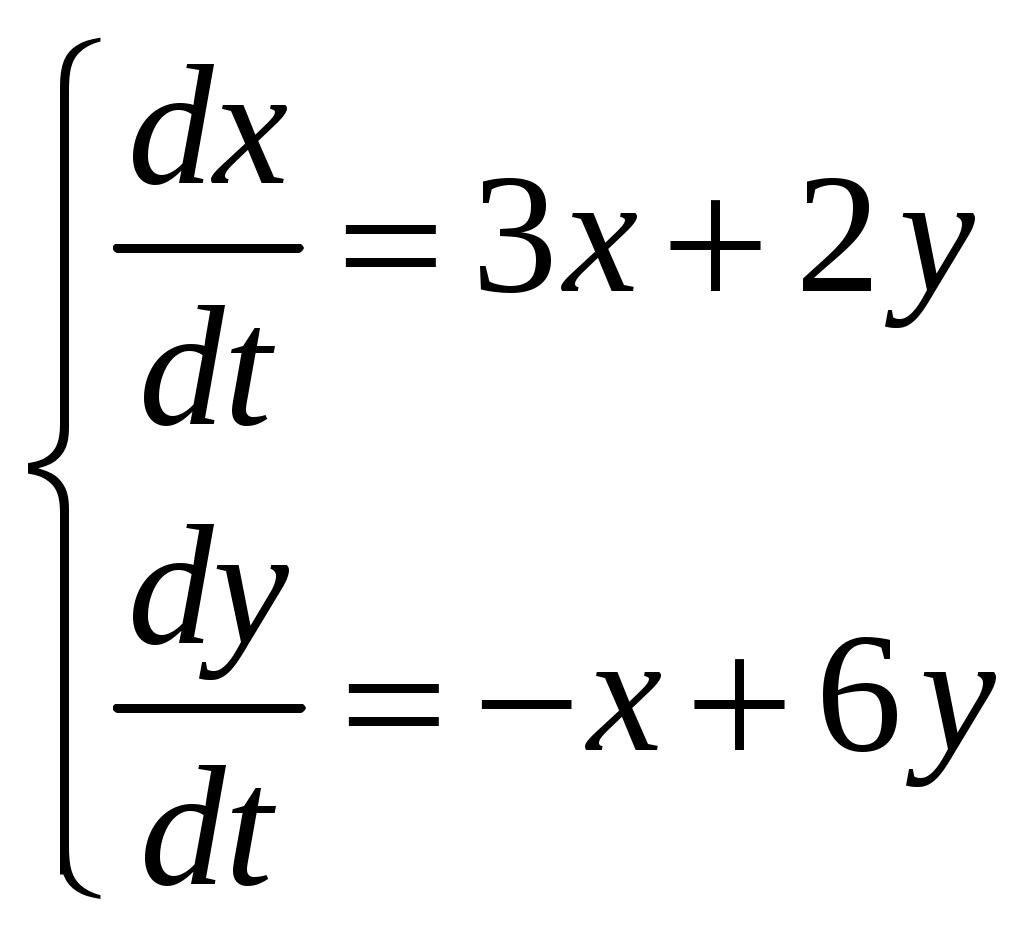 .Решение. Характеристическое уравнение для заданной системы уравнений:  . , , . – собственные значения.Найдем собственные векторы из системы: 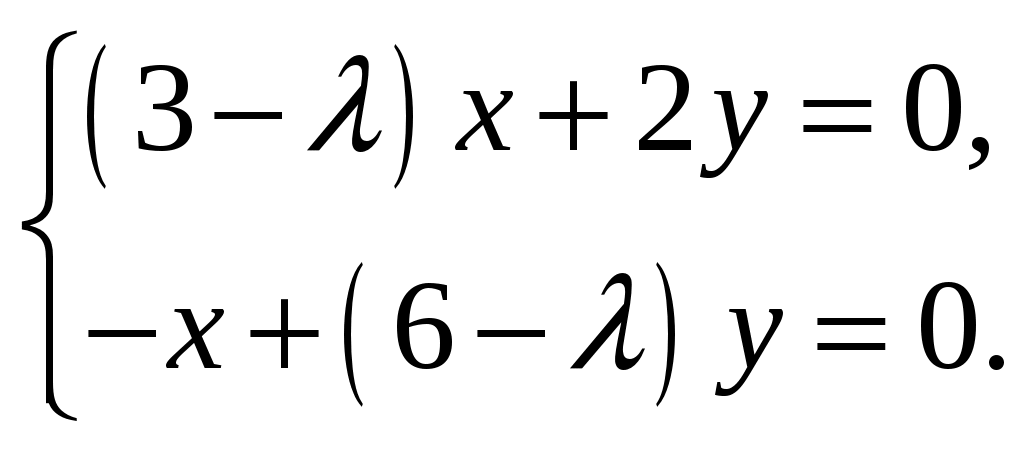 При  имеем: При  получим:  , тогда .При  имеем: При получим:  , тогда .Общее решение системы ДУ в векторном виде имеет вид:  В координатном виде: 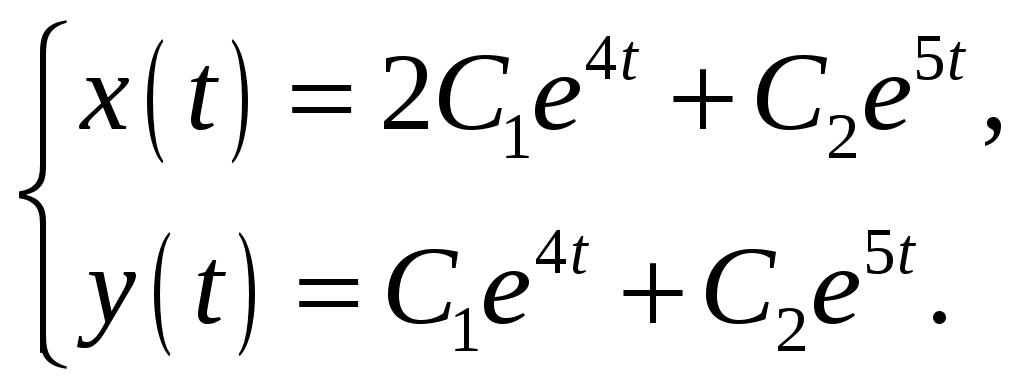 Контрольная работа №6. 1.  .Решение. Воспользуемся признаком Даламбера. Так как 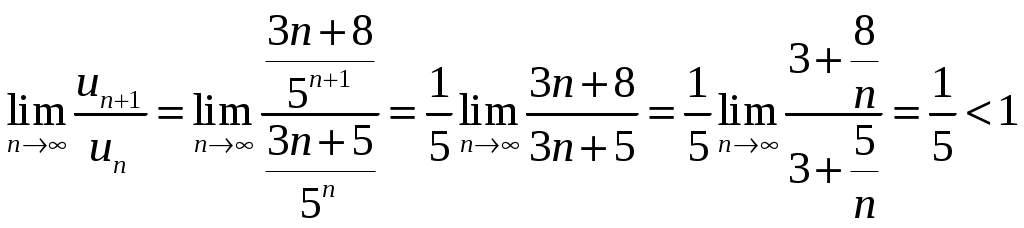,  , то  принимает вид: , поэтому исходный ряд сходится.Ответ: ряд сходится Исследовать на абсолютную и условную сходимость: 11. 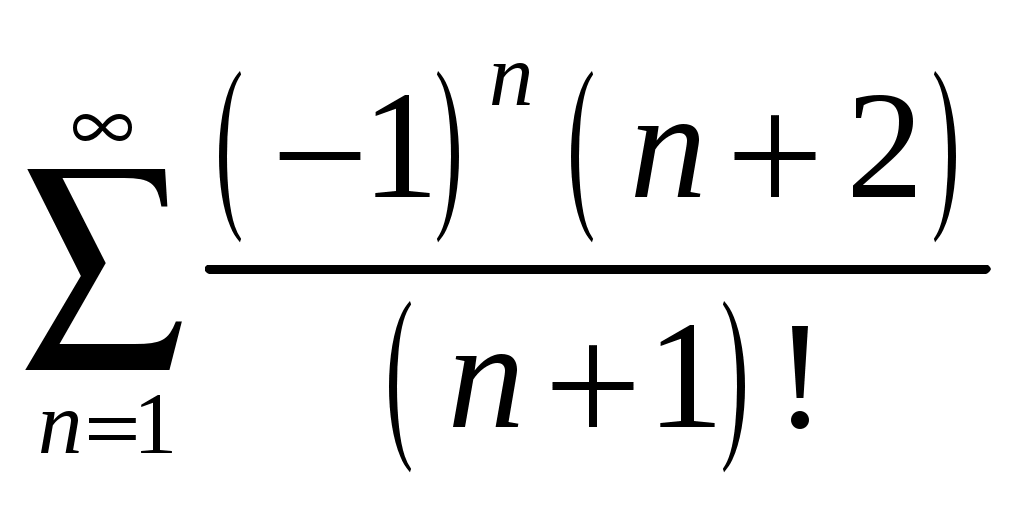 .Решение. Ряд знакопеременный. Составим ряд из модулей членов ряда:  Воспользуемся признаком Даламбера. Так как 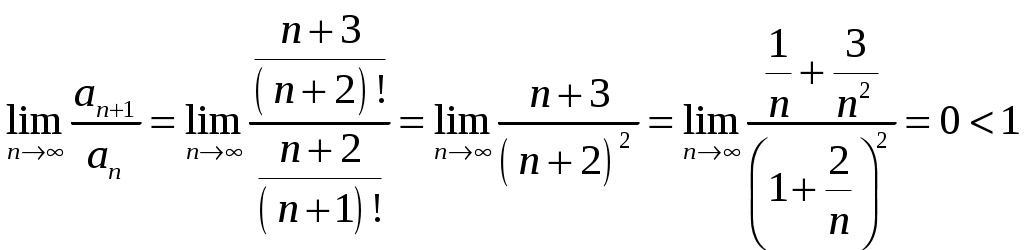 ,  , то  принимает вид: , поэтому ряд  сходится. Значит, заданный ряд сходится абсолютно. Ответ: ряд сходится абсолютно. Найти интервал сходимости степенного ряда  .21.  .Решение. Радиус сходимости степенного ряда можно найти по формуле:  . Т.к. 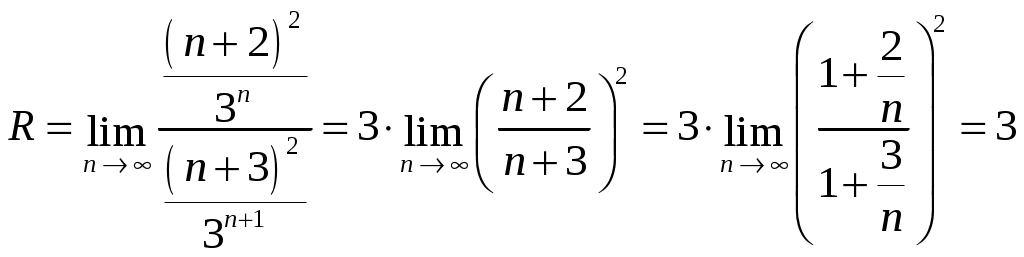и  , то .Итак, радиус сходимости ряда 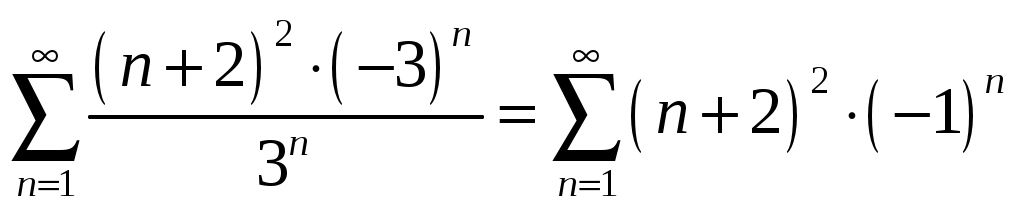 . Определим интервал сходимости данного степенного ряда: .Т.о.,  – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.Пусть  . Подставим в заданный степенной ряд и получим знакочередующийся ряд .Для членов полученного ряда:  В соответствии с признаком Лейбница данный ряд расходится и 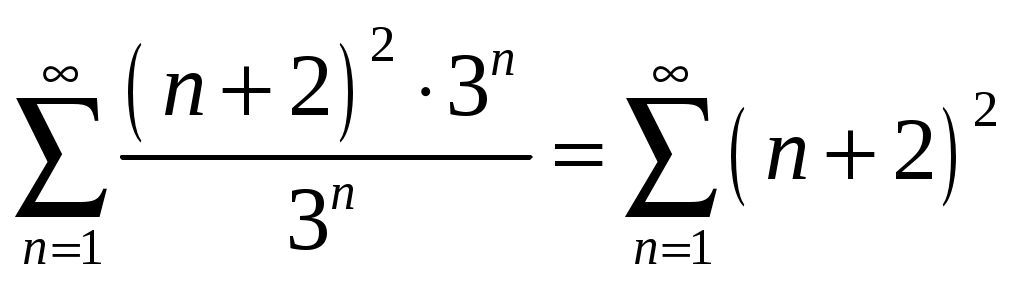не принадлежит области сходимости степенного ряда.Пусть  . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами: Получили расходящийся ряд, так как не выполняется необходимое условие сходимости  . Следовательно, ряд расходится и не принадлежит области сходимости степенного ряда. Итак, областью сходимости данного степенного ряда является промежуток .Ответ: .Вычислите определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно:31.  ,  .Решение.  Воспользуемся разложением подынтегральной функции в ряд. Используем формулу: 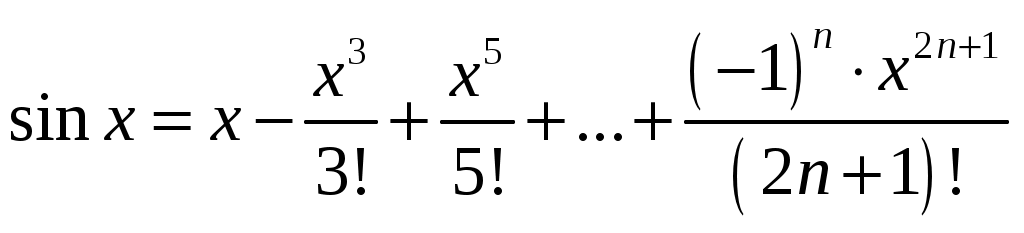 Получаем: 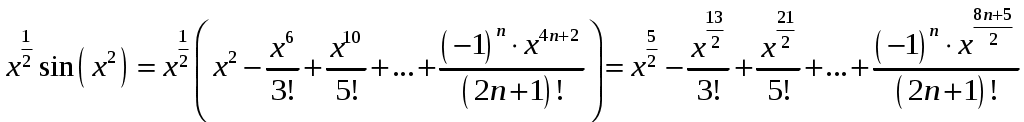 Тогда заданный интеграл: 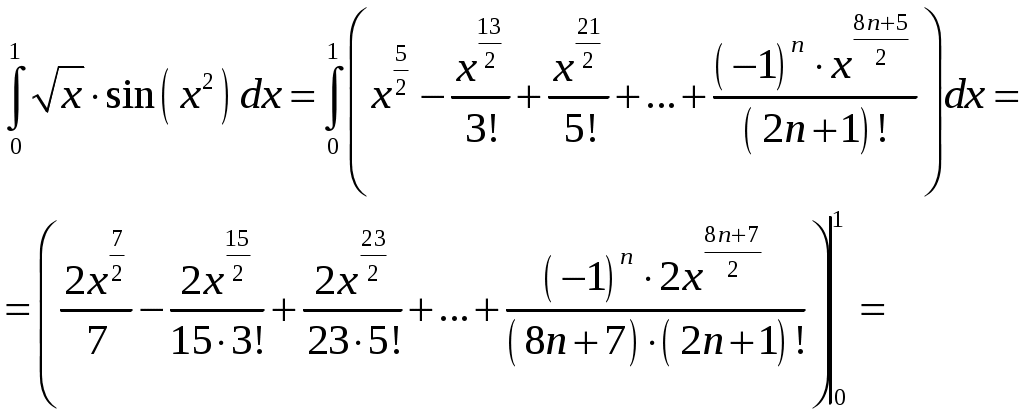 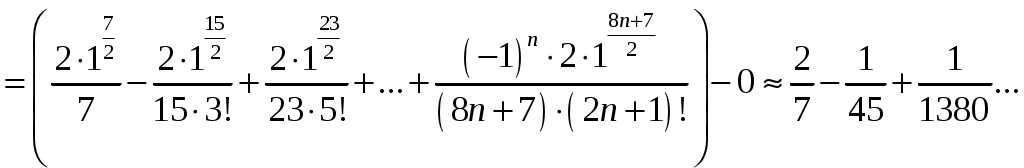 Т.к. третий член разложения  , то заданный интеграл будет: Ответ: 0,263. Найти первых три, отличные от нуля члена разложения в степенной ряд функции  дифференциального уравнения  , удовлетворяющего начальному условию  :41.  ,  .Решение. Из уравнения видно, что неизвестная функция  имеет производные любых порядков. Значит, ее можно разложить в ряд Маклорена: Из заданного уравнения С учетом начальных условий при х = 0 получаем  .Из заданного уравнения находим: При х = 0:  . При х = 0 :  .Подставим найденные значения  в формулу  и получим искомое решение: Ответ:  Разложить данную функцию  в ряд Фурье на данном интервале:51.  ,  .Решение. Разложение функции  на интервале  в ряд Фурье имеет вид: .Найдем коэффициенты по формулам:  , , .Находим коэффициенты: 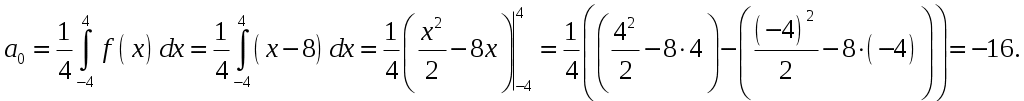 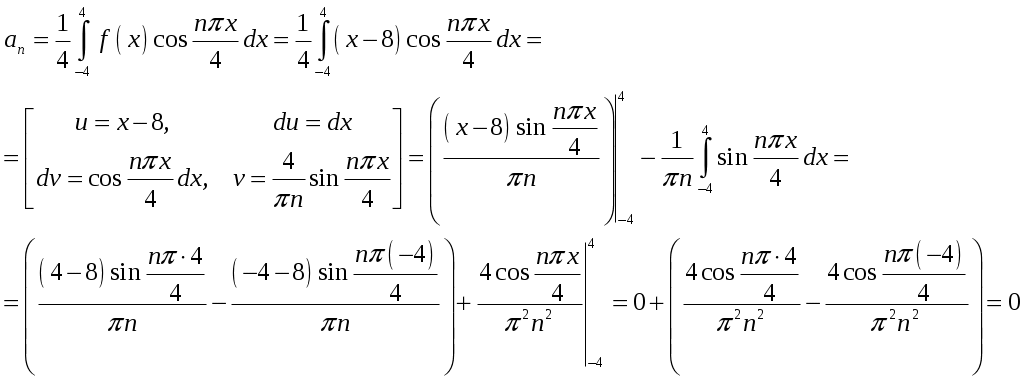 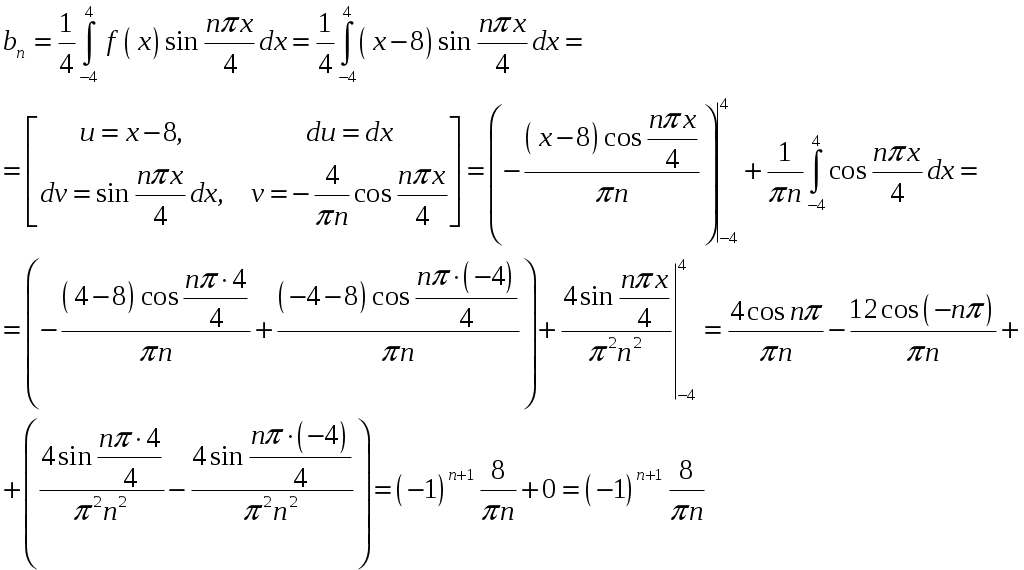 Разложение функции в ряд Фурье примет вид: 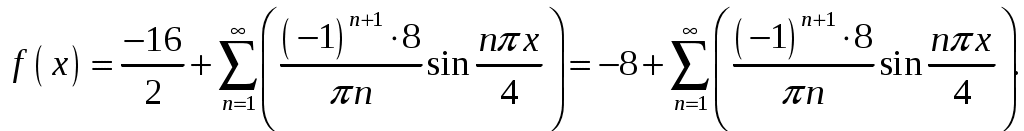 . |