Контрольная работа по теме Дробные рациональные уравнения. Контрольная №6. Контрольная работа 6 Вариант 1 Решите уравнение а б 3
 Скачать 46.04 Kb. Скачать 46.04 Kb.
|
|
Контрольная работа № 6 В а р и а н т 1 1. Решите уравнение: а)  ; б) ; б) 2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В? В а р и а н т 2 1. Решите уравнение: а)  ; б) ; б) 2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч. В а р и а н т 3 1. Решите уравнение: а) 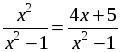 ; б) ; б) 2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В? В а р и а н т 4 1. Решите уравнение: а)  ; б) ; б) 2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч? Решение вариантов контрольной работы В а р и а н т 1 1. а)  . Общий знаменатель х2 – 9. . Общий знаменатель х2 – 9.х2 = 12 – х; х2 + х – 12 = 0. По теореме, обратной теореме Виета, х1 = 3; х2 = –4. Если х = 3, то х2 – 9 = 0. Если х = –4, то х2 – 9 ≠ 0. б) 6х + 5(х – 2) = 3х(х – 2); 6х + 5х – 10 – 3х2 + 6х = 0; –3х2 + 17х – 10 = 0; 3х2 – 17х + 10 = 0. D = (–17)2 – 4 · 3 · 10 = 289 – 120 = 169, D 0, 2 корня. x1 = 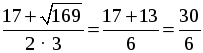 = 5; = 5;x2 =  . .Если х = 5, то х (х – 2) ≠ 0. Если х = О т в е т: а) –4; б) 2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил 162(х – 3) – 120х – х(х – 3) = 0; 162х – 486 – 120х – х2 + 3х = 0; х2 – 45х + 486 = 0. D = (–45)2 – 4 · 486 = 81, D 0, 2 корня. x1 = 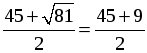 = 27; = 27;x2 = 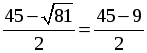 = 18. = 18.Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста). О т в е т: 18 км/ч. В а р и а н т 2 1. а)  . Общий знаменатель х2 – 16. . Общий знаменатель х2 – 16.3х + 4 = х2; х2 – 3х – 4 = 0. По теореме, обратной теореме Виета х1 = 4; х2 = –1. Если х = 4, то х2 – 16 = 0. Если х = – 1, то х2 – 16 ≠ 0. б) 3х + 8(х – 5) = 2х(х – 5); 3х + 8х – 40 – 2х2 + 10х = 0; –2х2 + 21х – 40 = 0; 2х2 – 21х + 40 = 0. D = (–21)2 – 4 · 2 · 40 = 441 – 320 = 121, D 0, 2 корня. x1 = 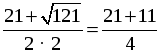 = 8; = 8;x2 = = 2,5. Если х = 8, то х (х – 5) ≠ 0. Если х = 2,5, то х (х – 5) ≠ 0. О т в е т: а) –1; б) 2,5; 8. 2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 3) км/ч, по течению – (х + 3) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение: + = . Общий знаменатель х (х – 3)(х + 3). 12х(х + 3) + 5х(х – 3) = 18(х – 3)(х + 3); 12х2 + 36х + 5х2 – 15х – 18х2 + 162 = 0; х2 – 21х – 162 = 0. D = (–21)2 – 4 · 162 = 441 + 648 = 1089, D 0, 2 корня. x1 = = 27; x2 = = –6. Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи. О т в е т: 27 км/ч. В а р и а н т 3 1. а) 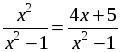 . Общий знаменатель х2 – 1. . Общий знаменатель х2 – 1.х2 = 4х + 5; х2 – 4х – 5 = 0. По теореме, обратной теореме Виета, х1 = 5; х2 = –1. Если х = 5, то х2 – 1 ≠ 0. Если х = –1, то х2 – 1 = 0. б) 5х – 8(х – 3) = 3х(х – 3); 5х – 8х + 24 – 3х2 + 9х = 0; 3х2 – 6х – 24 = 0; х2 – 2х – 8 = 0. По теореме, обратной теореме Виета, х1 = 4; х2 = –2. Если х = 4, то х (х – 3) ≠ 0. Если х = –2, то х (х – 3) ≠ 0. О т в е т: а) 5; б) –2; 4. 2. Пусть х км/ч – скорость, с которой велосипедист ехал из А в В, тогда (х + 4) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение: – = 1. Общий знаменатель х (х + 4). 48(х + 4) – 40х – х(х + 4) = 0; 48х + 192 – 40х – х2 – 4х = 0; х2 – 4х – 192 = 0. D1 = (–2)2 + 192 = 196, D10, 2 корня. x1 = 2 + = 2 + 14 = 16; x2 = 2 – = 2 – 14 = –12. Ни один из корней не обращает знаменатель в нуль, но корень х = –12 не удовлетворяет условию задачи. О т в е т: 16 км/ч. В а р и а н т 4 1. а)  . Общий знаменатель х2 – 4. . Общий знаменатель х2 – 4.5х + 14 = х2; х2 – 5х – 14 = 0. По теореме, обратной теореме Виета, х1 = 7; х2 = –2. Если х = 7, то х2 – 4 ≠ 0. Если х = –2, то х2 – 4 = 0. б) 8х – 10(х – 3) – 2х(х – 3) = 0; 8х – 10х + 30 – 2х2 + 6х = 0; 2х2 – 4х – 30 = 0; х2 – 2х – 15 = 0. По теореме, обратной теореме Виета, х1 = 5; х2 = –3. Если х = 5, то х (х – 3) ≠ 0. Если х = –3, то х (х – 3) ≠ 0. О т в е т: а) 7; б) –3; 5. 2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 2) км/ч, по течению – (х + 2) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение: + = . Общий знаменатель х (х – 2)(х + 2). 15х(х + 2) + 6х(х – 2) – 22(х – 2)(х + 2) = 0; 15х2 + 30х + 6х2 – 12х – 22х2 + 88 = 0; х2 – 18х – 8 = 0. D1 = (–9)2 + 88 = 169, D10, 2 корня. x1 = 9 + = 9 + 13 = 22; x2 = 9 – = 9 – 13 = –4. Ни один из корней не обращает знаменатель в нуль, но корень х = –4 не удовлетворяет условию задачи. О т в е т: 22 км/ч. |
